
下载掌阅APP,畅读海量书库
立即打开




注 1:
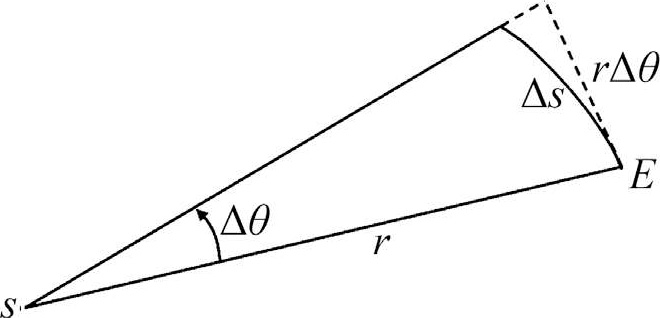
图 1-13 地球面积律示意图
如图1—13,地球—太阳连线瞬时扫过的面积Δ
S
近似扇形面积,即
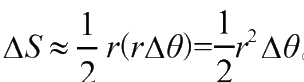 。当Δ
t
趋近于0时,取
。当Δ
t
趋近于0时,取
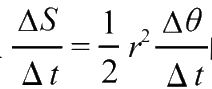 的极限,得到
的极限,得到
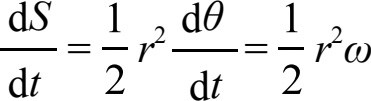
根据实测数据即地球绕日的角速度 ω 以及实算数据即太阳与地球之间的距离 r ,可以检视
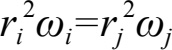
即日地连线在相同时间内扫过相等面积,得到地球面积律。
注 2:
开氏量天术简要说是因为地球和其他行星都在绕日运行,所以由地球观察各个行星的“视运动”就很奇怪,比如水星逆行,简称“水逆”,并不是水星真的逆道而行,而是我们在地球上看到的一种行星视运动。由于水星运行轨道与地球自转成一定的黄道角度差,所以站在地球上看,水星就好像在反向移动,这就是所谓的水逆。(顺便说一句,占星术里的水逆的含义毫无根据。)但是我们只要能充分掌握日地距离对于方位的变化规律,就可以研究其他行星的绕日运行,比如由日地距离可以计算出日水距离、日火距离等,因此就量天有术了。
注 3:
这里涉及大量的几何分析,由于与数据分析主题无关,因此省略。
注 4:
半长径即半长轴,是椭圆长轴的一半。半长径的长等于该行星离开太阳的平均距离。