





我们常常会碰到乍一看令人震惊的巧合:你和3位朋友一起吃饭,结果发现4人穿了同样颜色的衣服;你梦见自己的孙子,第二天他就突然打来电话;你的两位同事在同一天都接到要去参加陪审团的通知;你发现你老板的新娘和你是小学同学。这些事情让我们或惊或喜,或疑或思,但怎么会这样呢?
从概率的视角来看,我们首先应该问,这样的事难道不可能发生吗?所谓巧合,实属平常还是真的惊人?
对个人来说,在某种情况下,所发生的任何事都是意料之外的。
“我不信,”珍妮弗叫道,“小小的斯莫尔镇来的约翰·史密斯竟然赢得了彩票大奖!”
“哇,真牛!”你小心应道,“你认识他吗?”
“不认识,真不幸。”
“你以前听说过他吗?”
“没有,从来没有。”
“你以前去过斯莫尔镇吗?”
“没有。”
“那你为什么这么惊讶呢?”
“因为赢得彩票大奖的可能性只有约一千四百万分之一。”珍妮弗以权威的口气说道,“偏偏约翰·史密斯那家伙赢得了!”
不管是哪种商业型彩票,要赢得大奖几乎都是不可能的。但是,每天都有数百万的人买彩票,他们中通常又至少有一人会中奖。这倒一点也不会让我们吃惊,为什么呢?因为数百万人中方有一人赢得了大奖。每人都有数百万分之一的机会赢得大奖,所以当然通常会有某个人赢得啦。
将一枚硬币连掷10次,如果每次都是正面朝上,那可是非常惊人的,因为这种事情发生的概率只有1/1024(每次掷硬币,正面朝上的概率都是1/2,连乘10次)——不到0.1%。然而,如果你一整个下午不停地掷同一枚硬币,几个小时以后终于发现接连有10次正面朝上,那就一点也不奇怪了,因为那是必然之事。
所以,当有朋友告诉你一项惊人的发现时,你首先要问自己:概率是多少?也就是说,总共有多少次不同的机会让这件事——或其他类似的意外之情——发生?
在我14岁时,我们全家曾到佛罗里达州奥兰多市的迪士尼乐园游玩。两天的时间里,我们乘坐了可怕的过山车和舒缓的小火车,看到了闹鬼的房子、会唱歌的木偶,还吃了很多垃圾食品。意外的是,在数千陌生人当中,我们竟然遇到了父亲的堂兄菲尔一家。他们住在康涅狄格州,我们谁也没有想到会在佛罗里达州碰到。这样的巧遇让我们全都大吃一惊。
这到底有多令人震惊呢?当时美国有两亿三千万人口,所以在迪士尼乐园里随便选一个人,他恰好就是我父亲的堂兄菲尔的可能性只有两亿三千万分之一——小得让人难以想象。不过,在迪士尼乐园的两天时间里,我们在排队等待各种游乐项目时碰到过许多不同的陌生人。算下来至少有两千人曾与我们碰面,甚至认识,而他们中任何一人都可能会是菲尔。所以,遇到菲尔的可能性马上就增加了2000倍,变成十一万五千分之一了。
但是菲尔堂兄并不是我们唯一可能会遇到的人。我父亲的其他堂表兄弟,我母亲的堂表兄弟,或许还有其他亲戚。此外,还有我们的朋友、同事、邻居、同学、朋友的亲戚、邻居的朋友,等等。至少有500个像菲尔那样的人,这种相遇同样会让人大吃一惊。这就让相遇的可能性又增加了500倍,变成1/230了。
当然,1/230连1/100的一半还不到。所以在迪士尼乐园玩,大多数时候可能一个认识的人也碰不到,但在一生的旅行、参观和探险中,你一定会不时地与某人不期而遇。这其实并不那么令人吃惊。
“多少分之一”这个问题会以不同的方式出现。例如,有位朋友告诉我,就在她父亲去世前的那个晚上,父亲出现在她梦中,神色异常平静。有人可能会想,这个梦表明我那位朋友似乎“知道”她父亲要死了,或者甚至会想,这是她的父亲于500千米以外在潜意识里与她交流。
也许是这样吧。不过另一种解释是,我们每天晚上都会做很多梦。其中最有可能想得起或记得住或会与别人谈论的,正是这些与别的事情有着令人惊异联系的梦。暂且假设我那位朋友每50个晚上会做一个梦见她父亲的梦。那么她在父亲去世前的那个晚上,正好梦见他的可能性只有1/50。然而,在她的一生中,某个时间点做某个与某些事情有关的梦的可能性却大得多。所以,问题在于,总共多少个梦里面才会有一个令人印象深刻的梦?
诺贝尔奖得主、物理学家费恩曼(Richard Feynman)曾记录下在学生时期发生的一件事。一天,突然有一种感觉告诉他,祖母死了。就在那时,电话响了。他的预感是真的吗?他的祖母死了吗?不,电话是找另一个学生的,费恩曼的祖母还是好好的。这一故事很好地说明了尽管我们经常会有预感、会做梦、会作推测,但那些与现实不符的往往会忘掉。偶尔有一次成为现实,我们就会忘记这只是许多预感中的一个,因此结果就显得令人惊讶了。
现在考虑一个经典的物理问题。取一小杯水倒入海里。渐渐地,水流、浪潮、下雨、蒸发就把世界上所有的水混在了一起。5年后,你到世界另一面的某处海边,再取一小杯水。那么,前一杯水中的水分子,现在有多少出现在后一杯水中呢?
全世界的海水约有10亿立方千米之多。相比之下,一杯水简直不值一提:它在1后面跟22个零这么一个总份数中大约占两份。前一杯水中的任何一个特定的水分子会在后一杯水中出现的可能性相当于这么一个分数,分母是1后面跟22个零,分子是2。这个概率实际上趋近于零。
另一方面,水分子又小得难以想象,即使只有一杯水,里面的水分子也多得不得了——大概有1后面跟25个零那么多。事实上,正因为前一杯水中有这么多的水分子,5年后,全凭偶然,它们中还是会有1000多个水分子会出现在后一杯水中。1000个水分子现在听上去好像很多,但它们是多少分之一呢?
我们能用类似的理性概率逻辑来分析神奇的爱情吗?许多人都有这样的经历,他们未来的伴侣是在一种很不可能的场景下“碰巧”遇上的。就我自己来说,尽管我的妻子玛格丽特(Margaret)和我以前曾在一个晚会上照过面,我们之间的爱情却是在另一个机缘下开始的。有天下午,我 碰巧 陪一个朋友去邮局寄包裹,他也是 碰巧 给一个同事帮忙。当时,玛格丽特也是 碰巧 提前下班,又 碰巧 要去邮局办点私事,而她去的邮局又 碰巧 与我们去的是同一家(这个邮局离她家与她工作的地方都不近)。
我陪朋友去办事的概率有多大?玛格丽特当天也去同一家邮局的概率有多大?在那天的同一时刻我们都在那里的概率有多大?将所有这些因子乘在一起就可得出,我和玛格丽特在那天相遇的概率最多只有数十万分之一。
但是,它就是发生了。我该怎么解释呢?噢,我 可以 坚持说,即使我们没有在邮局相遇,以后的某一天也会在别处相遇,比如另一个晚会上。我也可以断言,在我每星期的东奔西跑当中,某些时候肯定会遇到什么趣事。我也可以冷静地宣称,每个人事实上都有许多潜在的合适的伴侣,早晚你总会遇到其中的一个。不过,以上的这些说辞好像都不怎么令人信服。我猜我只是一个幸运的家伙罢了。
有时我们会发现一些关系链,表面看来颇为惊人。比如,你发现隔壁邻居是你兄弟的管家的堂兄。对此,我们什么时候该感到惊讶、什么时候又不该感到惊讶呢?
有些关系链更有趣。在影片《星球大战》里面,邪恶的维德(Darth Vader)向英雄天行者(Luke Skywalker)宣称“我是你父亲”时,这一关系的揭示出人意料,令人印象深刻。在此片的搞笑版、布鲁克斯(Mel Brooks)的《星球歪传》( Spaceballs )里,赫尔米特勋爵(Lord Dark Helmet)说“我是你父亲的兄弟的侄子的堂兄的前室友时”就很平凡(从而成为一处笑点)。对这两句听上去相似的道白,我们的反应为什么会如此不同呢?
我们再来解释一下,这种关系的概率是多少?每人都只有一位父亲。对于我们来说,尽管与父亲同等重要的人物可能还有母亲、兄弟姐妹、子女甚至终身密友,但父亲的地位仍非常崇高,在近亲中肯定可以排在前十位。所以,如果我们的头号大敌关系与我们这么近,那当然就非常令人震惊了。另一方面,对于我们来说,有许多人的重要性等同于我们“父亲的兄弟的侄子的堂兄的前室友”。所以,当达克·赫尔米特勋爵说出他是关系这么远的一个角色时,我们只会当他是非常庞大的关系群中的一人。没有理由为此惊讶,我们也确实没有惊讶。不过,和我们的关系与此类似的人到底有多少?能与我们通过较短的关系链相联系的人又有多少?
这一问题与六度分隔现象有关,该理论源于哈佛大学心理学家米尔格朗(Stanley Milgram)在1967年做的一个实验。他把包裹寄给在堪萨斯州和内布拉斯加州随机选出的一些人,要求他们尽量把包裹转寄给住在马萨诸塞州的某个指定的人。问题是,转寄包裹的人只知道收包裹者的姓氏。
 所以,堪萨斯州转寄包裹的人就要考虑:我有哪个熟人可能会与另一个人相熟,那个人又与别的某人相熟,别的某人最后又与马萨诸塞州的目标人物相熟?
所以,堪萨斯州转寄包裹的人就要考虑:我有哪个熟人可能会与另一个人相熟,那个人又与别的某人相熟,别的某人最后又与马萨诸塞州的目标人物相熟?
米尔格朗发现,每个成功寄到的包裹平均要经过6个人的手。“六度分隔”的概念就是这样产生的,它激起了人们极大的好奇心:原来我们彼此之间都能通过较短的链相连,比如“朋友的朋友的朋友”或“同事的同事的同事”。
米尔格朗的实验有很多缺陷。它限制在一个国家,并且有很多包裹最后并未寄到,这可能仅仅是因为中间的人对实验不感兴趣,但也可能意味着需要转手更多的人才能把包裹寄到(但并未实现)。另一方面,收到包裹的人要自己决定再把包裹寄给谁,他们无法知道自己的选择能否让前后经手的人最少。总的来说,大多数科学家都接受米尔格朗的实验结论,就是我们彼此之间都能通过较短的关系链相连,尽管精确的数字6的真实性值得怀疑。
现在,我们换另一种方式来看看这种联系。比如,假设每个人都有500个“朋友”,也就是彼此相熟的人。那么朋友的朋友关系链就有500×500,即25万之多,而朋友的朋友的朋友关系链就有500×500×500,也就是1.25亿。这里面当然会有某些不同的关系链最后指向同一个人,所以你的朋友的朋友的朋友总数要少于1.25亿——但还是多得吓人。即使把全世界的人都考虑进去,六度分隔理论仍极有道理。
数学家们喜欢这样的关系链,他们还以卓越的匈牙利数学家埃尔德什(Paul Erdös,1913—1996)的工作为出发点,建立了自己独特的关系链。埃尔德什的一生,都在拎着一个行李箱去拜访世界各地的数学家。这些数学家要照顾埃尔德什的日常生活,埃尔德什以帮他们解决研究中遇到的问题作为回报。最终,埃尔德什与世界各地的数百名数学家联合署名发表了1500多篇数学论文。

有感于这种广泛的联系,数学家们发明了 埃尔德什数。 每位曾与埃尔德什合写过论文的数学家,埃尔德什数都是1(这样的人有500多位);每位曾与埃尔德什数为1的数学家合写过论文的数学家,埃尔德什数都是2(这样的人有7000位左右);照此类推。我自己的埃尔德什数是3:我在1999年与数学家佩曼特尔(Robin Pemantle)合作发表过一篇论文,他在1996年与数学家詹森(Svante Janson)合作发表过论文,后者又在同一年与埃尔德什合作发表过论文。因此,从我到埃尔德什就形成了一个3位数学家链。可惜的是,这并非什么了不起的成绩,有33000多位数学家的埃尔德什数也都是3。
这里还要提及的是,电影爱好者们也有自己的类似于埃尔德什数的发明,即 贝肯数。 每位曾与演员贝肯(Kevin Bacon)合作出演过一部影片的人,贝肯数是1;每位曾与贝肯数为1的演员合作出演过一部影片的人,贝肯数是2;照此类推。例如,萨兰登(Susan Sarandon)的贝肯数是2,因为她与潘(Sean Penn)合作出演过《死囚漫步》( Dead Man Walking ),后者又与贝肯合作出演过《神秘河》( Mystic River )。
类似的概念还可以应用到其他许多不同的对象上。比如,互联网上的链接(用网页浏览器从你的网页到我的网页,中间要点击多少次超链接)。例如一起录过音的摇滚乐手,查尔斯(Ray Charles)到奥斯伯恩(Ozzy Osbourne)只要3步链接,因为查尔斯与杰克逊(Michael Jackson)一起录过音,杰克逊与重金属乐队吉他手斯拉施(Slash)一起录过音,后者与奥斯伯恩一起录过音;还有,曾在同一个队效力的棒球运动员,从1930年代的强击手鲁斯(Babe Ruth)到现在的明星投手克莱门斯(Roger Clemens),可以找到好几条不同的5步链接路径;还有对于与梦露(Marilyn Monroe)的链接步数,但出于礼貌,我就不再详细解释。
要在不同种类的人群之间找到不同种类的联系,其结果似乎是一切皆有可能。这给“巧合”提供了一种全新的视角:有那么多可能的联系,因此它们偶尔真的发生也就不奇怪了。
有一个众所周知的关于概率的有趣事例,即 生日问题。 随机选择23个人,他们当中有两个人同一天过生日(只看月和日,不看年)的概率要超过50%;如果有41或更多的人,两人同一天过生日的可能性将超过90%。据此可以设计一出不错的小把戏。下次你再去参加一个规模不小的室内晚会时,记得找一位没听说过生日问题的可怜的傻瓜,然后跟他打赌,说房间里肯定有两个人同一天过生日;接下来,你就等着数钱吧。
为什么这种概率会那么高呢?这个问题也是一个多少分之一的问题?不过这一次的答案有些让人难以捉摸。最初我们可能会想,一年有365天(不考虑闰年),23个人的生日只占据365天当中的23天,也就是6.3%。这是一个非常小的数,我们前面设计的那个小把戏能有效吗?令人生疑。然而,上述答案是对的,只是问题问错了。如果你问23个人,他们当中是否有人在 今天 (或圣诞节,或其他特定的一天)过生日,那么说是有人的概率确实只有6.3%。
这一事实曾帮我“破案”。在一次开统计学会议的晚餐期间,有3个人庆祝生日,这让我起疑。当时聚餐的只有180人,从统计学上看,恰好在那一天过生日的只可能有180/365人,也就是约半个人。我的怀疑是对的,我后来发现,那几位“寿星”中有两位的生日其实是在下个月,他们只是想利用过生日来发点财。
可是在这个小把戏中,我们问的是23个随机选择的人中,是否有两人的生日在同一天——没有指定是哪一天,比如今天或圣诞节。由这一差别就可以解释相应的可能性为什么会那么高了。
奥妙其实在于 对子数 要比单个人数多得多。例如,假设晚会上有4个人:埃米,贝提,辛迪和德比。他们可以配成6个对子:埃米—贝提,埃米—辛迪,埃米—德比,贝提—辛迪,贝提—德比,辛迪—德比。人越多,配成的对子也越多,且多得多。有23人参加晚会,可配成253个对子;41人参加晚会,可配成820个对子。(对子数是这样算的,由总人数乘以比总人数少1的那个数,再除以2。如总人数为4,对子数就是4×3÷2=6;总人数为23,对子数就是23×22÷2=253;总人数为41,对子数就是41×40÷2=820。)
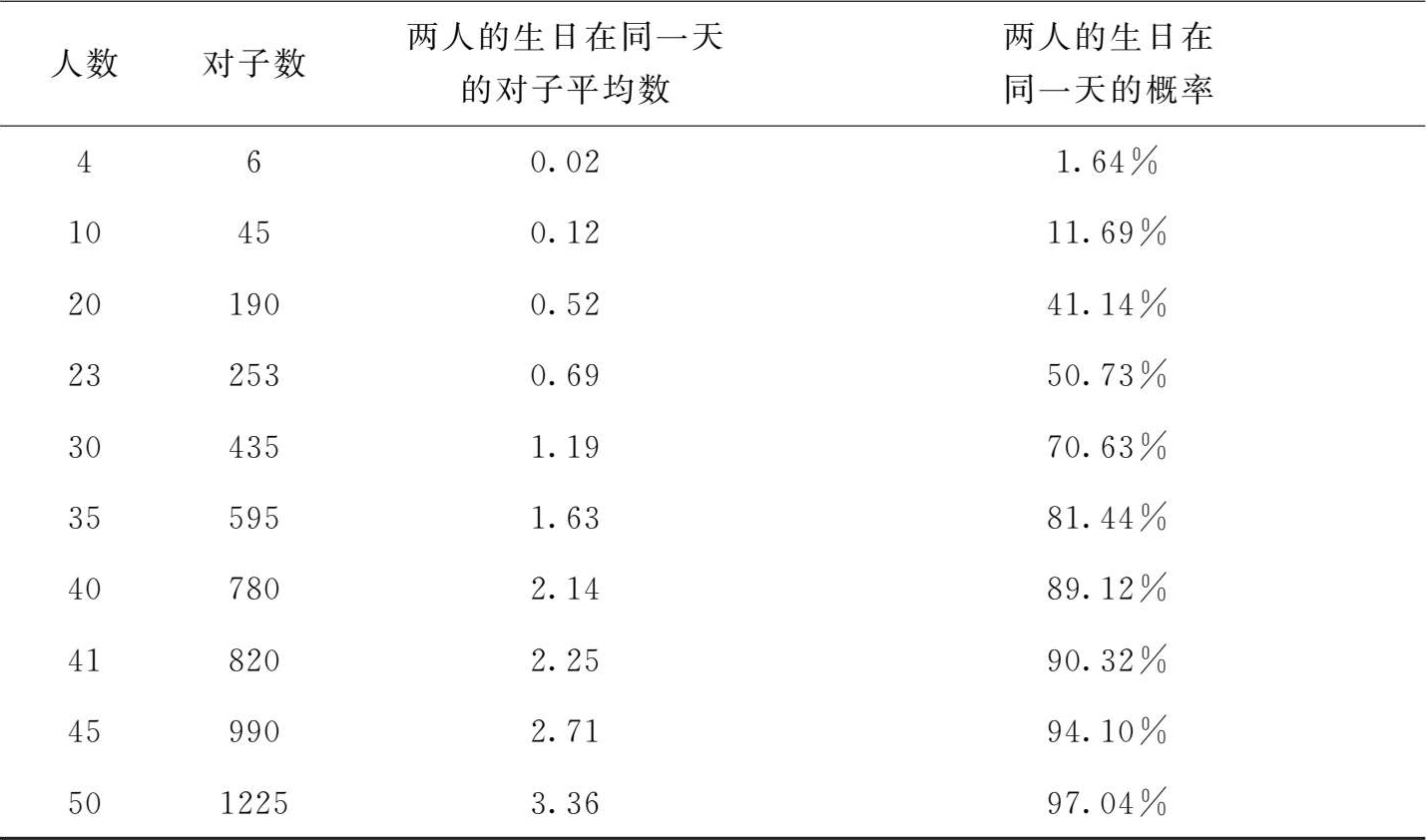
现在,我们来看看生日问题是怎么回事。尽管只有23个人,但他们能配成253个 对子。 每个对子中两人的生日恰好在同一天的概率是1/365;平均算来,两人生日在同一天的那些对子总共有253/365,也就是0.69个。0.69远大于0.5,这表明有两人的生日在同一天的概率大于50%。0.69这一数字其实有些过,因为可能会有不同的几对人,他们的生日都在同一天。作出修正后可以得出,23人中有两人的生日在同一天的概率是50.7%。若有41人参加晚会,平均算来,两人的生日在同一天的那些对子共有820/365,也就是2.25个,而至少有两人的生日在同一天的概率就是惊人的90.3%。
表2.1 生日问题的数据
由生日问题可以看到,匹配成功的概率——生日、收入、家乡、爱读的小说、口袋里的零用钱,还是其他事——要远远高出你的想象,因为可能的对子太多了。所以下一次如果有两样不同的事项正好相匹配,不要惊讶。相反,问问你自己,总共有多少个对子?
你很兴奋,因为你买了一台超级数字音乐播放器。你急忙下载了4000首喜欢的乐曲,然后按下键,随机播放。随着吉他的反复和小鼓的独奏振动着你的耳朵,一首辉煌的交响乐响起。你期待着听到一首首不同的乐曲,这是多么的幸福啊。
在听到第75首乐曲时,你发现,这是已经播放过的第42首乐曲。总共4000首乐曲,仅仅播放了75首就开始重复,真是一台愚蠢的播放器。怎么会是这样?这台播放器肯定有问题!
在找商家退款前,你做了一些计算。75首乐曲可以配成2775个对子,比总共4000首乐曲的一半还要多。在4000首乐曲中随机选择75首,其中至少有两首一样的可能性是50.2%。
所以,播放器也许不该受到责备。你还是戴上耳机继续听吧。
2003年11月的头一个星期,大多伦多都市区发生了5起不相干的杀人案件。通常来说,该地区的杀人案件每星期只会发生1.5起。这一消息经媒体广泛报道后,人们开始担心正有一波犯罪浪潮汹涌袭来。多伦多市的警察局长呼吁对法庭审判系统进行公开的调查,说它“没有产生明显的威慑力”。这样的反应合理吗?
在回答此问题之前,我们先来猜猜下面的一个谜。图2.1所示为两个不同的点集,各有100个点。其中一个点集中的点完全是随机放置的,每个点在盒子中出现在某一地方的可能性都一样,另一个点集中的点是有意放置的。哪个点集是随机的?是左边还是右边?
在图2.1左边的点集中,各处点的分布表现出不同的形态。在一些地方,两三个点挨得很近。在有些地方,大片的区域中只有寥寥几个点。另外,图下方的那些点看起来几乎是螺旋形排列,而不像是随机放置的。
相比之下,右边那个点集中的点分布得很好。没有哪个点与另一个点挨得很近或很远,也没有哪片区域显得太稀疏。这些点似乎很好地展示了随机性,但事实上,左边点集中的点才是随机放置的。在这个点集中,每个点被放置在盒中的任何一个地方的可能性是相同的,且与其他点无关。那些挨得很近的点、稀疏的区域、螺旋形等,都是由偶然造成的。而右边点集中的点并不是随机放置的。我先画一个网格,然后把那些点均匀地画在各个格子里,再让每个点随机地略微移动一下(以免排列得太过完美)。因此,右边点集中点的分布只有很 微弱 的随机性(骗骗眼睛是够了),它们其实是经过精心安排,以高度非随机性的方式均匀地分布在整个方框中。

图2.1 哪个点集是随机的,左还是右?
这一例子表明,在很多事项(比如点)出现的地方,它们中的一些往往会偶然地聚在一起,这不能说明它们之间存在什么趋势、原因或联系。随机性欺骗了我们,我们所看到的形态、关系只是偶然的存在,别无深意。概率学家把这种现象称为 泊松簇。 相应的精确概率( 泊松分布 )最早是由法国数学家泊松(Siméon-Denis Poisson)于1837年计算出来的。
泊松簇能让某些人胆战心惊。我曾担任一家在线赌博网站的顾问,经理怀疑计算机在挑选基诺球(Keno balls)时出了问题。那些球应该以相同的概率随机地选出,但是经理发现有太多的球来自展示板上靠近17号的位置,他担心狡猾的赌客会利用这一点。经理的担心其实是多余的;精确的统计分析表明,那些球确实是以相同的概率随机地选出来的。经理看到的只是泊松簇在起作用罢了。
多伦多的那些杀人案件又是怎么回事?泊松分布告诉我们,如果每星期平均会发生1.5起杀人案件,那么全凭偶然,某一星期会发生5起杀人案件的概率仍有1.4%。所以,不出意外的话,每71个星期就有1个星期会发生5起杀人案件——几乎一年一次!多伦多杀人案真的不该那么令人震惊,它也没有暗示什么,只是运气差。
相比之下,一星期连一起杀人案件都不发生的概率要超过22%。确实,多伦多已有许多个星期没有发生过一起杀人案件了,但我还是看到报纸上的头版头条在惊呼“本星期仍平安!”
理解泊松簇的另一种方法是借助对子或更大的群体概念。在图2.1中,左边方框里有100个点,它们能配成4950个对子。在这样多对子中,有一些对子中的点挨得很近也就不足为奇。同样,一年发生78起杀人案件,它们能配成3003个对子,而由它们中的任意5起杀人案件组成的群则有2100万个之多。因此,这么多群中有一个群的5起杀人案件全都发生在同一星期,也就不怎么令人吃惊了。
泊松簇还能用来解释许多不同的事情。好几个星期你都没有接到晚会邀请,突然有两三个晚会都邀请你去,而且全在同一个晚上。你开车好几个小时都没遇到什么阻碍,突然在几分钟之内接连碰到两个差劲的司机。一天中有5个不同的人都对你态度粗暴。你在同一晚上接到3个电话,都是拨错了号码。你在公共汽车站等了25分钟也没等到一辆车,你满怀沮丧,突然却看见有三辆车没理由地连着开来。这些事情没有什么神秘的,也毫不惊人,也说不上出人意外。它们都只是概率的规则产生的结果。
说到公共汽车,泊松簇还能用来解释时刻表的重要性。如果公共汽车有规律地运行,每10分钟来一辆,那你等车的时间就是0到10分钟,平均5分钟。然而,如果公共汽车的运行完全各自为营,没有时刻表,情况就不同了。幸运的话,立即就会等来一辆车(甚至几辆车);不幸的话,就得等上很长一段时间。在这种情况下,等车的平均时间可能是10分钟——恰好是公共汽车按时刻表运行时的等车时间的 两倍。 所以,如果你所在城市的公共汽车运行很随意,可以向市长投诉,说你等车的平均时间毫无必要地拉长了一倍。
我们已经看到,许多所谓的巧合都纯属偶然。表面上惊人的结果也许只是众多可能性中的一个(比如在迪士尼乐园里遇到我父亲的堂兄),或者源于那么多对子(比如生日问题),或者应归因于泊松簇(比如每星期发生的杀人案件数目,点的螺旋形状)。
有时候,巧合的发生是因为两件看来不相干的事实际上有着共同的起因。房价猛跌,银行收益却猛增,二者都应归因于利率的调高。坐飞机的人数与参观博物馆的人数都在同一个星期飙升,那是因为正好放春假了。
有时这些 共同的起因 非常不起眼,人们很少注意到——但它们恰恰能用来解释看似惊人的巧合。下一次如果有两人或更多的人突然提出同样的建议,讨论同样的问题,或是采取同样的行动,那就问问自己,是否有什么共同的起因能用来释疑。
你终于找到了一个保姆来照顾杰森。此刻,你正与丈夫坐在一家高雅的法国餐厅,享受着难得的宁静与浪漫。
你惬意地轻摇着15美元一杯的红葡萄酒,不小心有几滴溅到白色的桌布上了。小小一片洇红让你想起去年杰森过5岁生日时的荒唐一幕,意大利面的酱汁大多是流到地毯上去了,而不是吃进孩子们的肚子里。
那天,杰森看上去很高兴。一个月后,他开始上幼儿园了,但看起来变得很焦虑。秋天,你和杰森的老师说起这一变化,她承认杰森在适应新生活上遇到了困难,但又说他看上去正在进步。
几个星期后在幼儿园的音乐会上,杰森很开心,他很喜欢这一活动。他与新结识的好朋友小哈尔多坐在一起。哈尔多看起来是一个不错的孩子。
哈尔多的父母是挪威人,他唱了一首传统的挪威民歌。尽管哈尔多不是什么伟大的歌手,但那首歌仍能唤起人们对于壮丽的峡湾以及幸福的人们的美好想象。斯堪的纳维亚应该是一个有趣的地方,哪天去看看。
“也许我们该去斯堪的纳维亚度假。”你的丈夫突然宣布道。你盯着他,很震惊。“啊,我也正想着斯堪的纳维亚呢!”你大叫道,“真是惊人的巧合!”
其实,你的丈夫也注意到了桌布上的那几滴红葡萄酒。他也想起了杰森的生日晚会,幼儿园的音乐表演,还有杰森的新朋友哈尔多……
即使没有什么共同的起因,综合应用“多少分之一”法则、泊松簇以及“朋友的朋友”那样乘幂似的关系链,也能对大多数的巧合作出解释。此种解释虽不能让巧合变得不再那么惊人,但能帮我们理解为什么巧合会那么频繁地发生。