




直线作为几何学的基本元素之一,值得研究。我们知道,同一平面上任何两条不平行的直线最终都会相交。当第三条直线与前两条直线相交于同一点时,我们就有三条共点线,它们有一个公共点。当三条以上的直线有一个公共点时,这种关系就变得更有趣了。我们从三角形的各种共点线开始,得出这些相当常见的共点性,然后将共点性的知识延伸到其他几何图形,此时,我们希望为读者提供一些令人感到意外和惊叹的想法。我们首先考虑一个三角形的三条高,即从三角形各顶点向对边所作的垂线。
最常见的共点性也许是一个三角形的三条高给出的。我们通常认为这个事实是理所当然的。不过,这是一个很好的例子,我们可以用它来开始对共点性的思考。在图1.1、1.2和1.3中,我们画出了三种基本的三角形:锐角三角形,它的所有角都小于90°;钝角三角形,它有一个角大于90°;以及直角三角形。每一个三角形都有三条高 AD 、 BE 、 CF 相交于 H 点。这个通常被叫作公共点的交点便是该三角形的垂心,它位于锐角三角形的内部、钝角三角形的外部和直角三角形的直角顶点处,如图1.1至1.3所示。
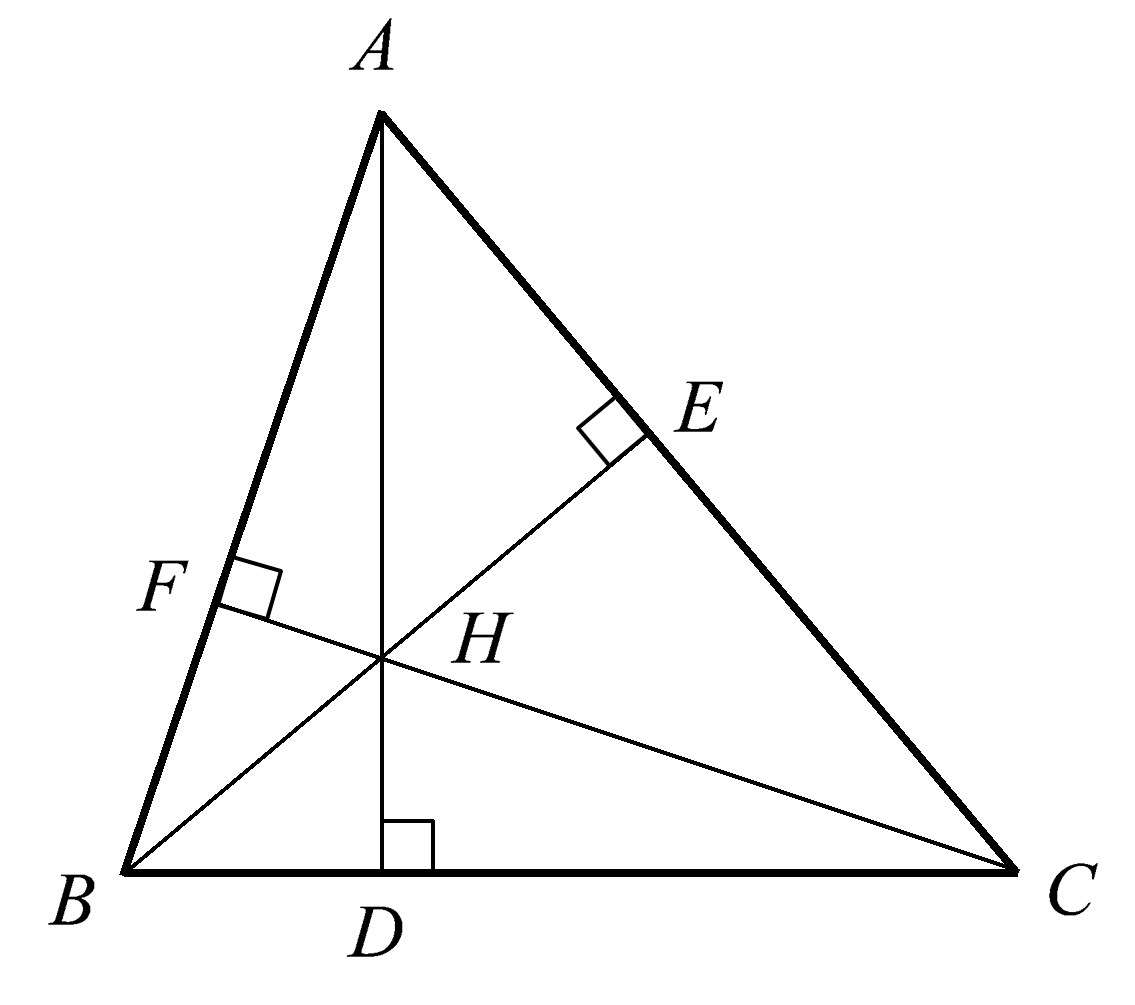
图1.1
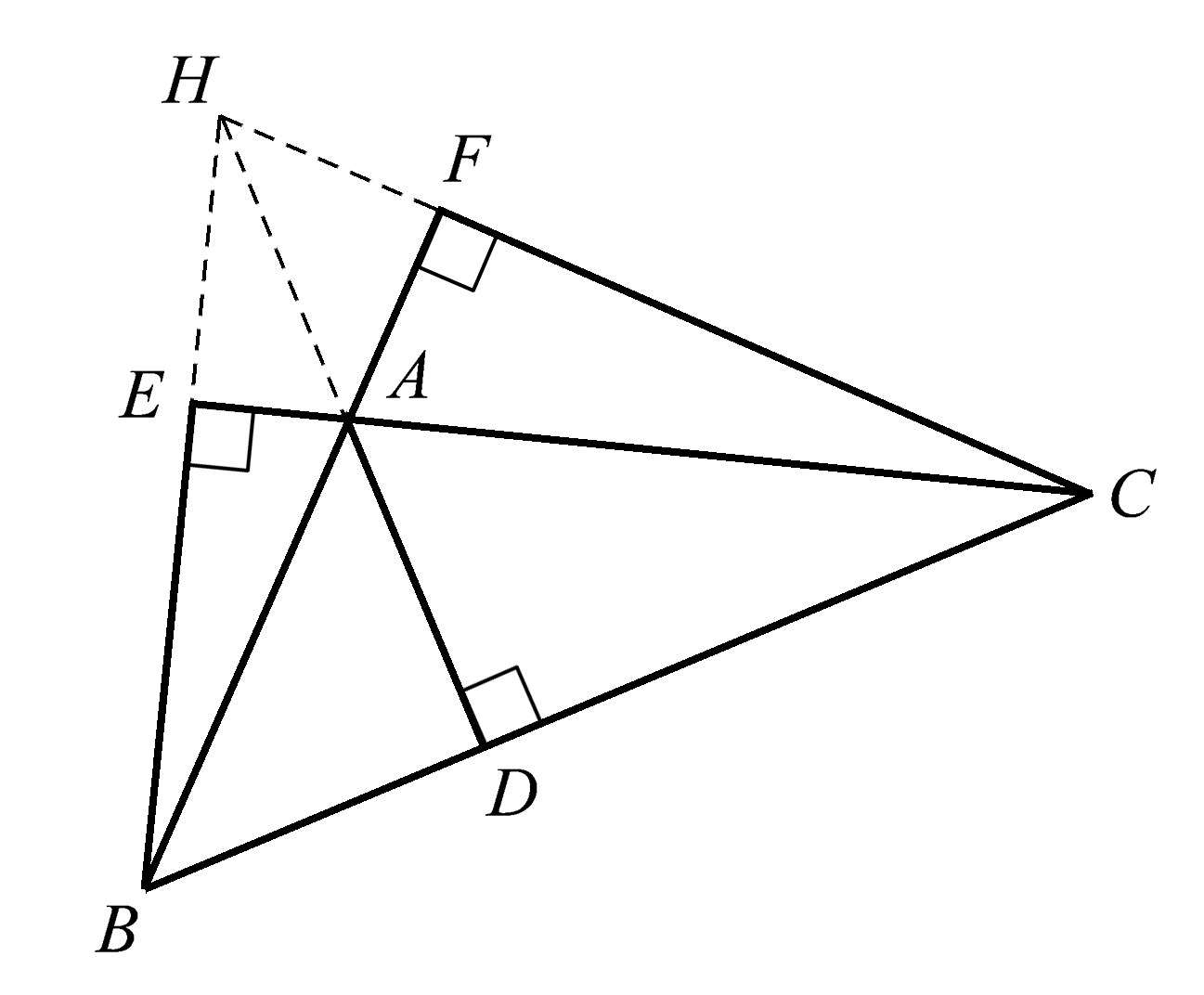
图1.2

图1.3
我们可以从高的这种关系中得出更多的信息。这个公共点特别有趣的地方在于,它将各条高分成了一些乘积相等的长度。尽管这一关系对图1.1、1.2和1.3中所示的三种情况都成立,但对于锐角三角形可能最容易看出: AH · HD = BH · HE = CH · HF 。
遗憾的是,尽管这种关系在讨论相似三角形时很容易得到,但它却很少出现在高中课堂上。另一种关系在高中几何中也没有提及,而它却能进一步提升你对三角形的三条高的认识。图1.1、1.2和1.3中所示的三角形还存在由垂足(高与对边相交的点)确定的交替线段之间的关系: BD 2 + CE 2 + AF 2 = CD 2 + AE 2 + BF 2 。

图1.4
高与三角形其他各部分的关系并不割裂。例如,在图1.4中,我们先作一个三角形的一条高(比如 AE )。然后我们作该三角形的外接圆和过顶点 A 的半径。出乎意料的是,当我们作三角形 ABC 的∠ A 的角平分线时,我们发现这条平分线也平分了我们刚刚构成的那个角∠ IAE ,或者换一种方式来表示,∠ EAD = ∠ IAD 。这也是在高中课堂上未能展示的许多关系之一,它还引出后续一些较为隐蔽的关系。
图1.5是三角形的一条高如何引出一条角平分线的另一个例子。如图1.5所示,三角形 ABC 的一条高 AD 上有任意一点 E ,连接 BE 、 CE ,其延长线分别与 AC 边和 AB 边相交于 P 点和 Q 点。此时高 AD 将平分∠ PDQ ,即∠ ADQ = ∠ ADP 。这个例子展示了三角形的高如何与一条角平分线相关联——在本例中,角平分线就是高!

图1.5
共点性有时以最奇特的方式出现。例如,如图1.6所示的三角形 ABC 。在这里,边 BC 延长到点 P ,点 P 可以在延长线上的任何位置。然后过点 P 任意作一条直线,分别与边 AC 和 AB 相交于点 D 和点 F 。当 DE 平行于 AB 、 FE 平行于 AC 时, EF 、 DE 、 BC 都包含点 E ,或者说它们共点于点 E 。回想一下,我们将点 P 选在 BC 延长线上的任何位置,这就是这个例子如此非同寻常的原因。

图1.6
还有许多其他关系也涉及三角形的高。例如,如果将任意一条高延长到原始三角形的外接圆上,则这条高所垂直的三角形的边( BC )将平分从垂心 H 到与外接圆的交点 G 的线段。请注意,在图1.7中,高 AD 上的点 D 便是 HG 的中点,即 HD = GD 。
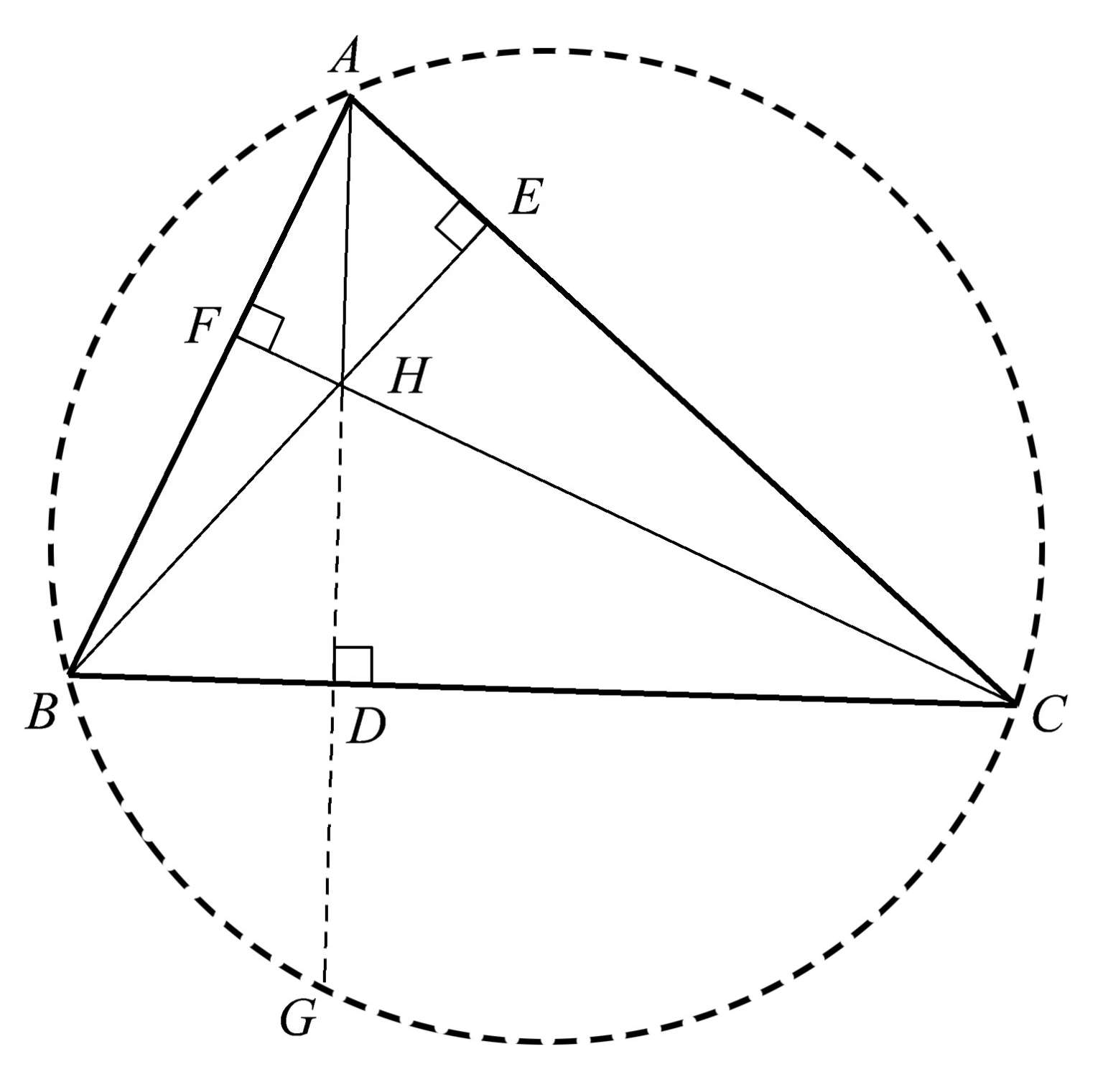
图1.7
如果我们延长另一条高,如图1.8所示,那么现在有两条高与外接圆分别相交于点 G 和点 J 。相当出乎意料的是,这确定了圆上的两条相等的弧 JC 和 GC ,即点 C 平分弧 JCG 。将任何三角形的两条高延长到外接圆,这个关系都成立。这就是为什么这一关系如此有趣。
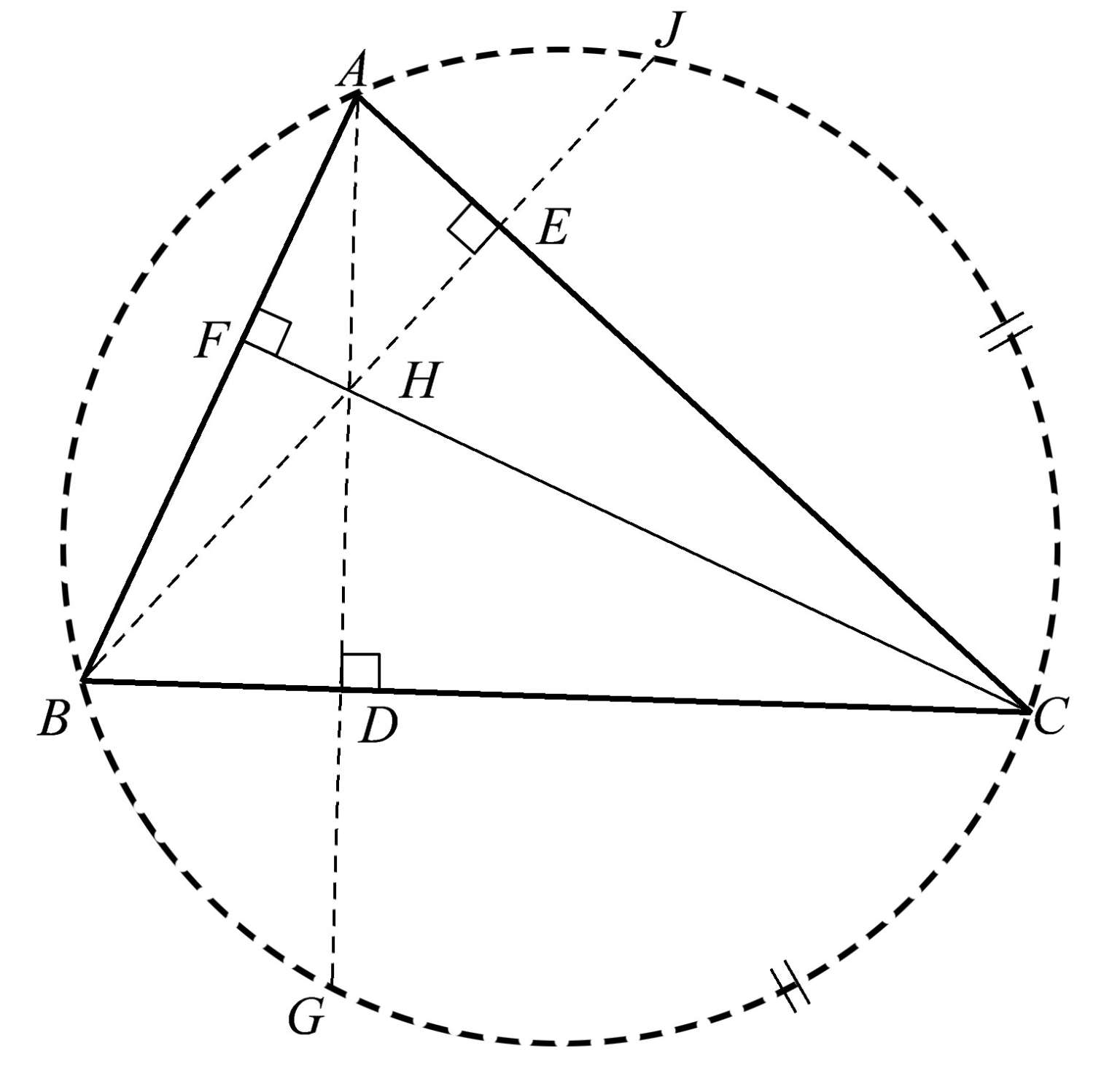
图1.8
假设我们现在把剩下的那条高 CF 延长,与圆相交于点 K 。当把三条高与外接圆的三个交点 J 、 K 、 G 连起来时,结果不仅会得到一个与垂足三角形 DEF 相似的三角形,而且这两个相似三角形的对应边平行。如图1.9所示。
图1.9中特别令人惊讶的是,由于这是一个锐角三角形,因此三角形 ABC 的各条高分别平分垂足三角形中相应的各个角。换言之,高 AD 平分∠ EDF ,高 BE 平分∠ FED ,高 CF 平分∠ DFE 。
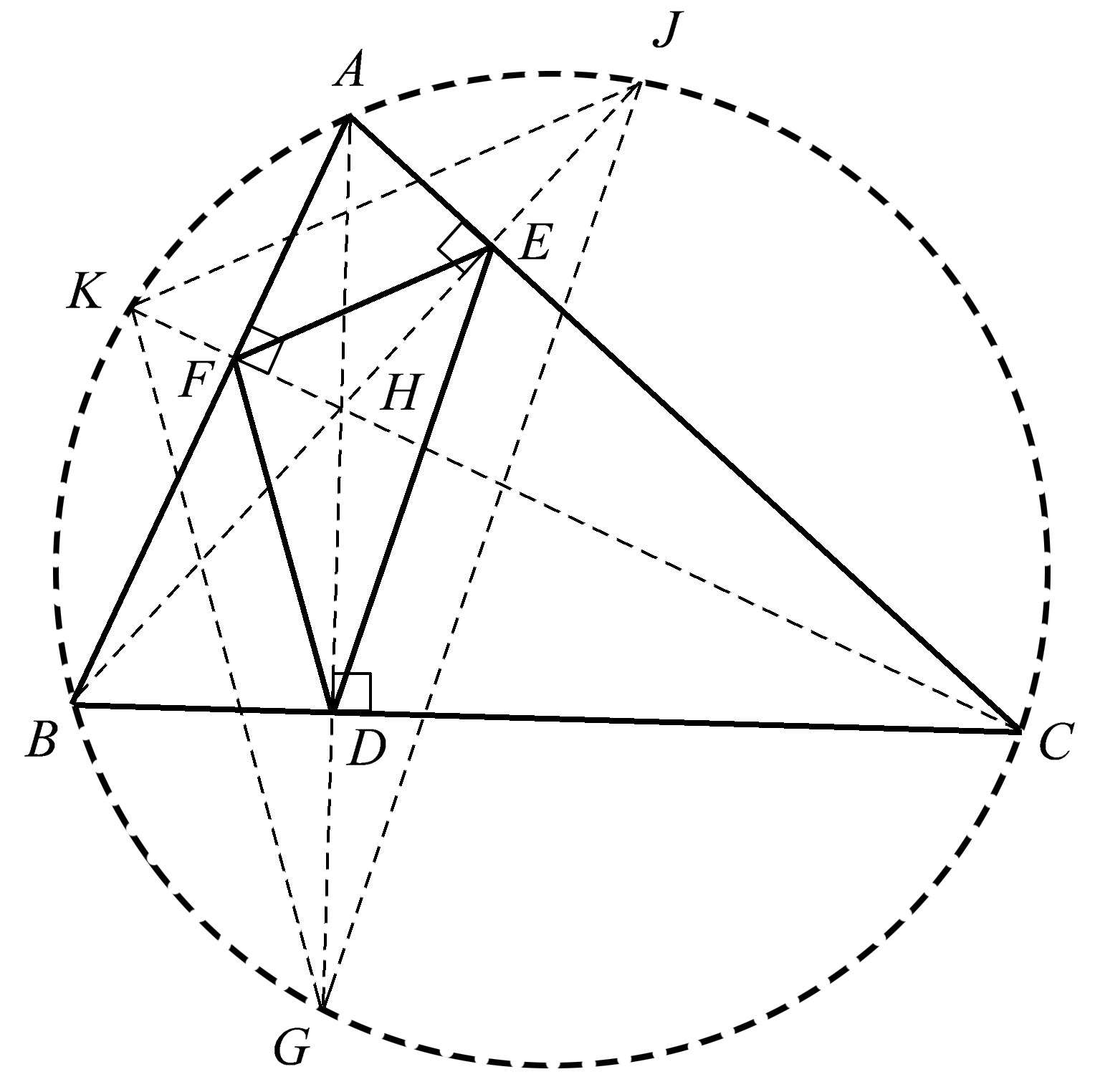
图1.9
垂足三角形的位置也很有趣:把三角形各顶点与该三角形的外接圆圆心相连接而得到的三条半径垂直于垂足三角形的各边。如图1.10所示,对于三角形 ABC ,把三个顶点 A 、 B 、 C 分别与外接圆 O 的圆心相连,得到三条半径,这些半径必然垂直于垂足三角形 DEF 的各边。这种简单而意想不到的关系大大提升了几何学之美。
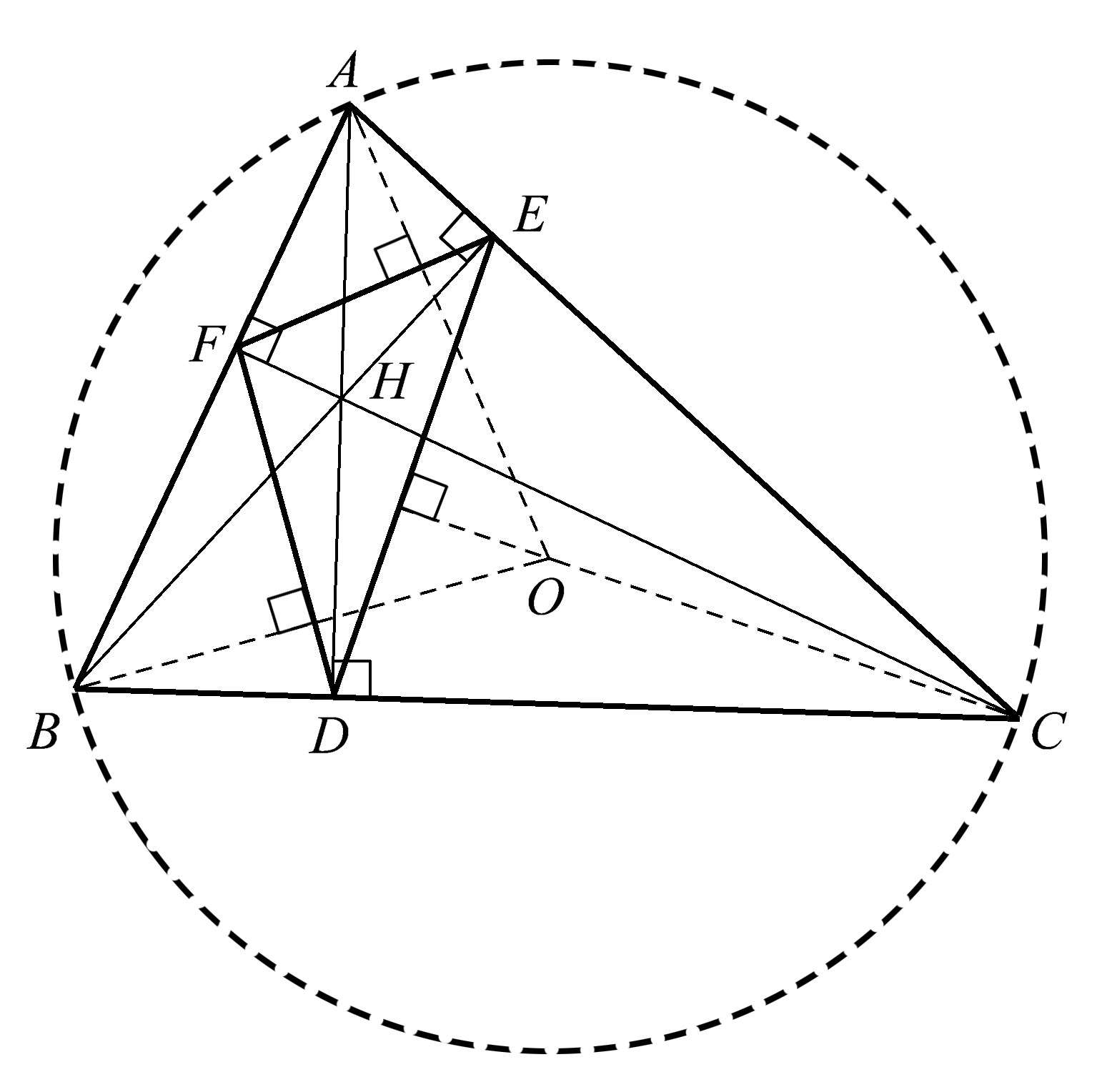
图1.10

图1.11
如果一个三角形的三个顶点分别在另一个较大三角形的三条边上,那么就说这个三角形内接于另一个三角形。在图1.11中,三角形 DEF 内接于三角形 ABC 。此外,三角形 DEF 的每个顶点都是三角形 ABC 的高的垂足。则在所有可能的内接三角形中,三角形 DEF 的周长最小。也就是说,三角形 DEF 的周长小于三角形 XYZ 或由三角形 ABC 各边上的任意三个点构成的其他三角形的周长。回想一下前面的一个例子,原始三角形 ABC 的每条高,即 AD 、 BE 、 CF ,分别平分垂足三角形的三个内角。
这里稍微离题一下,讨论一个有趣的问题。等边三角形 ABC 内的任意点 P (图1.12)到等边三角形三条边的垂直距离之和与该三角形内任何其他点(如 Q )到各边的垂直距离之和相等。这个距离之和总是等于该等边三角形的高的长度。因此,参考图1.12,我们可以将这一关系总结如下: PK + PH + PD = QJ + QG + QF = AE 。
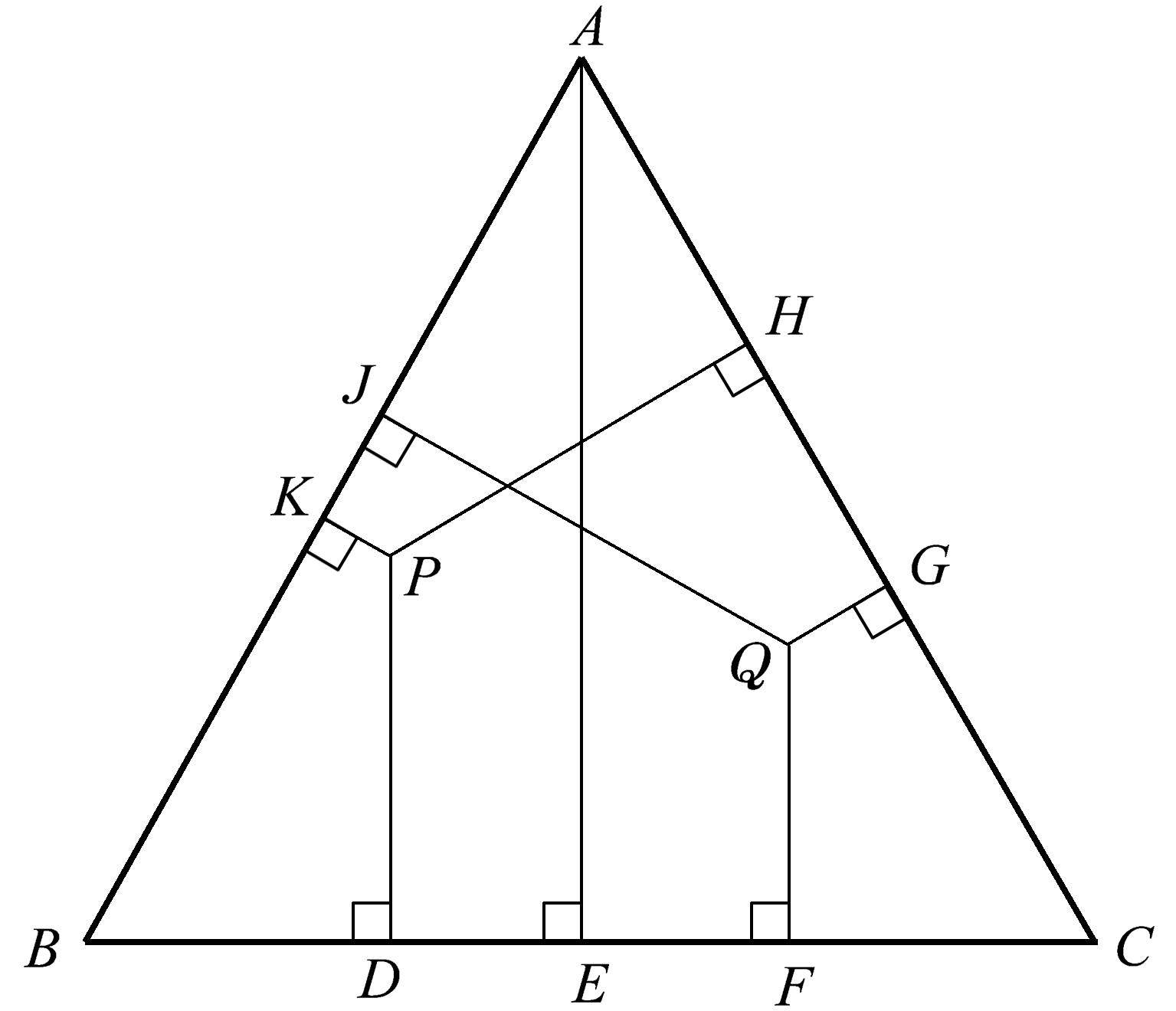
图1.12
以等边三角形的一条边为直径作一个半圆,就产生了一种特殊的关系。如图1.13所示,以等边三角形 ABC 的 BC 边为直径作半圆 BDC 。点 E 和 F 是线段 BC 的三等分点。然后我们连接 AE 与半圆相交于点 G ,连接 AF 与半圆相交于点 J 。令人惊讶的是,半圆也被这两条直线三等分,即弧 BG 、 GJ 、 CJ 是相等的弧。

图1.13
若要了解垂心与三角形其余部分的关系,请考虑两条高和一条边的中点。如图1.14所示,其中 N 是高 CF 的中点, M 是高 BE 的中点, K 是 BC 边的中点。众所周知,任意三个非共线点确定一个唯一的圆。不过,在这个圆上获得其他点并非易事。有趣的是,无论原始三角形 ABC 的形状如何,其垂心位于由三个非共线点 M 、 N 、 K 确定的那个圆之上。稍后我们将考虑更多的共圆点(位于同一个圆上的点)。
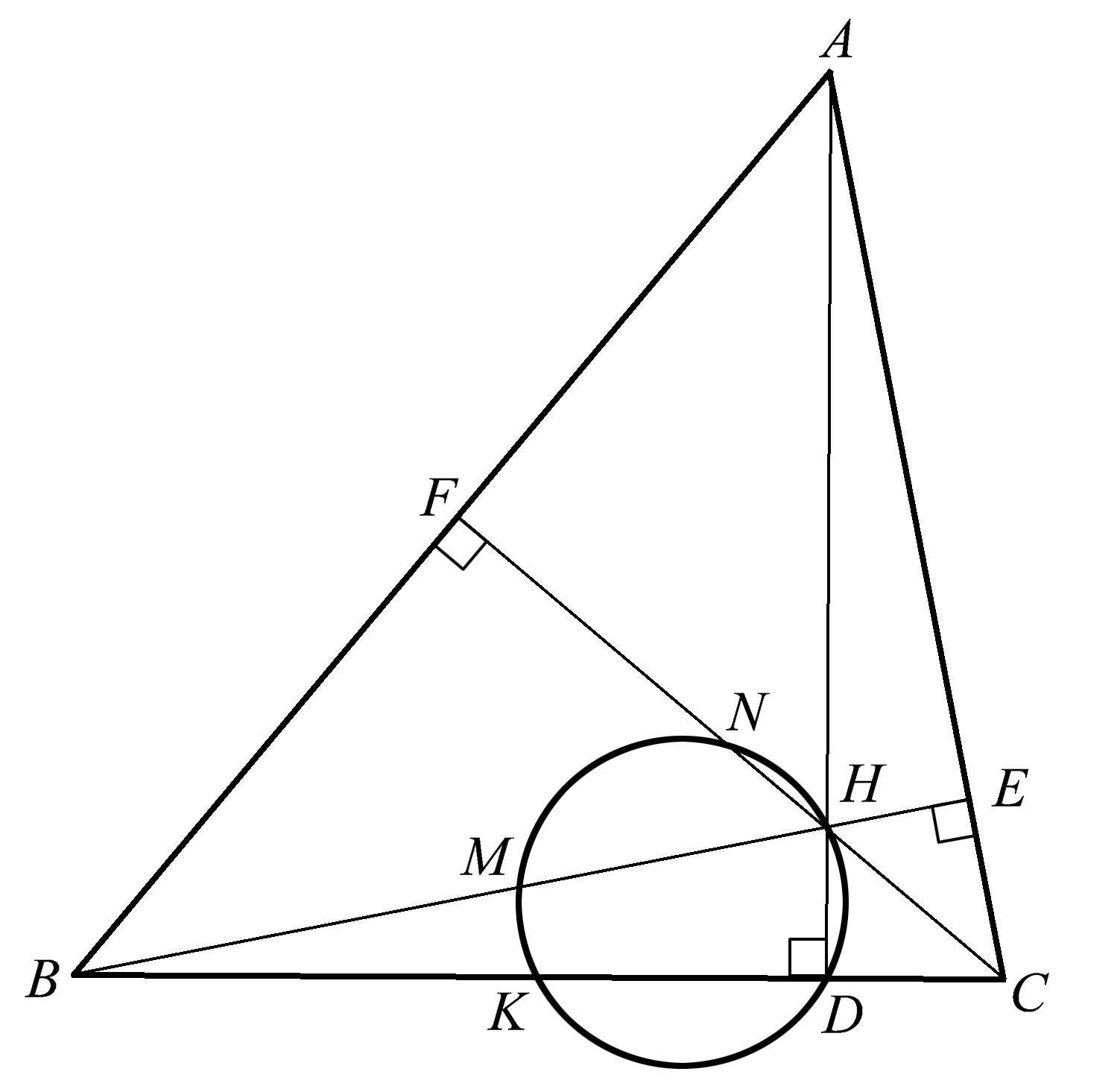
图1.14
一个三角形的三条高的交点(或者说垂心)有许多特殊的性质。其中有一条性质相当奇异。我们知道任意三个非共线点确定一个唯一的圆。图1.15中有三个由三角形的垂心和两个顶点所确定的圆。你会发现,这个由点 B 、 H 、 C 确定的圆,与三角形的外接圆(由点 A 、 B 、 C 确定)大小相等。对于由垂心和三角形 ABC 的一对不同顶点确定的其他两个圆(如图1.15所示),也有相同的关系,即图中的四个圆大小都相等。
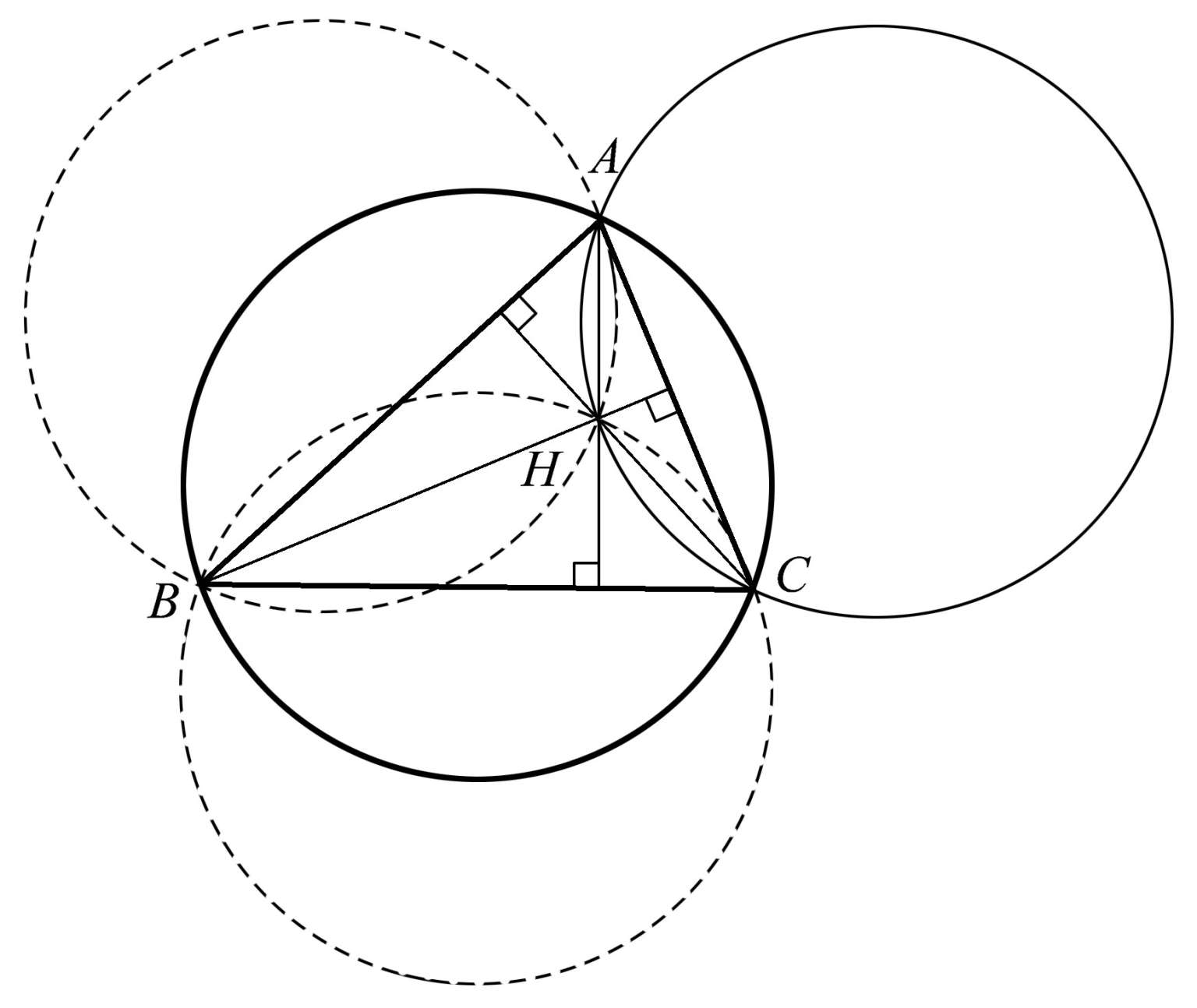
图1.15
关于一个三角形的各条高及其外接圆,还可以找到许多其他的关系。其中之一是从外心到三角形一边的距离是从垂心到相对顶点距离的一半。我们在图1.16中看到了这一点,其中外心
O
与
AC
边之间的距离
OG
=
 BH
。
BH
。
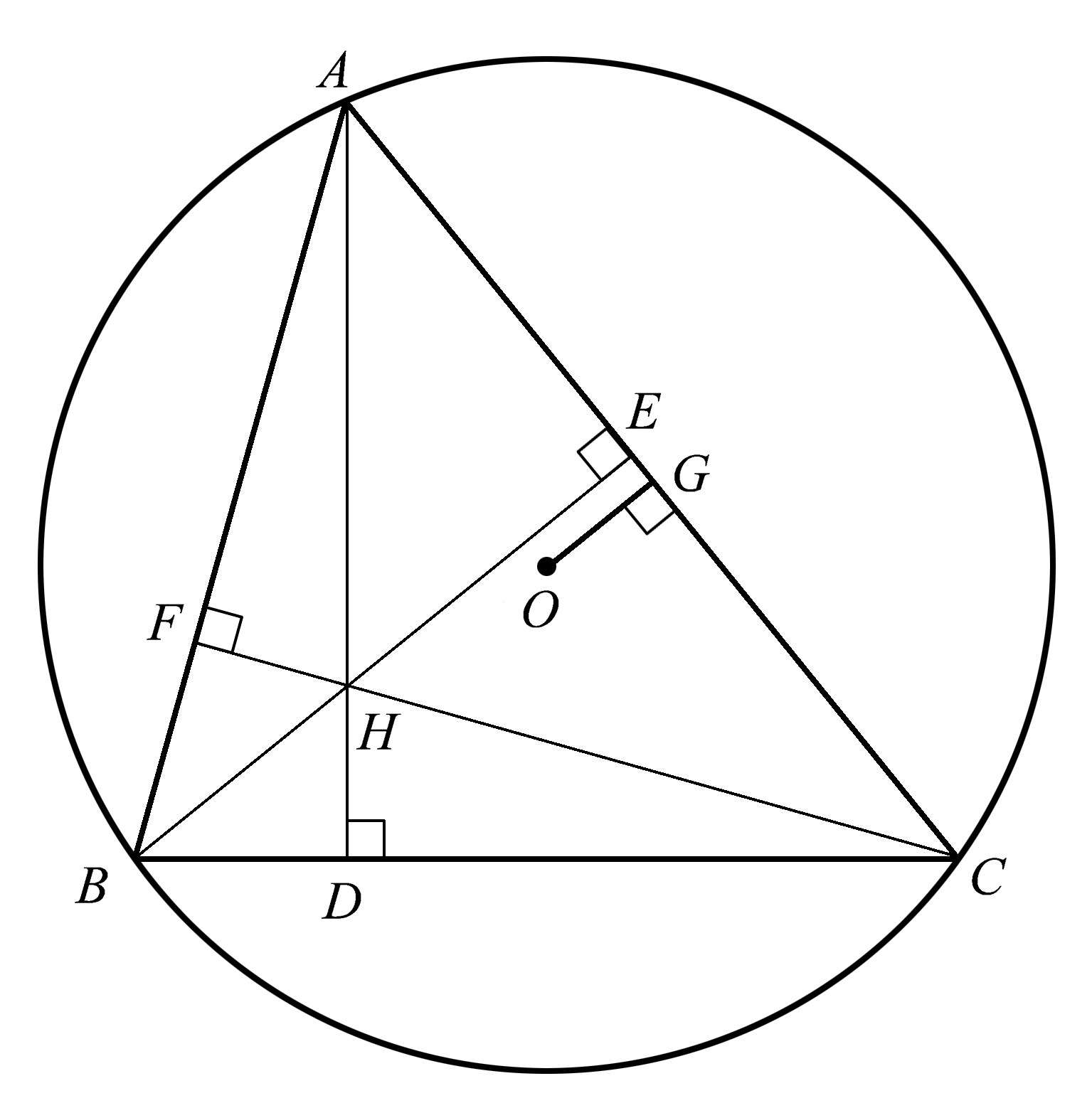
图1.16
我们已经看到,一个三角形的每条高被它们的公共点分成两段,而这两条线段长度的乘积对于所有高都相同。一个三角形的三条中线也交于一点,并且这个点将每条中线三等分。在图1.17中,三条中线
AD
、
BE
、
CF
相交于点
G
,它们的交点将每条中线三等分,因此
GD
=
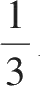 AD
、
GE
=
AD
、
GE
=
 BE
、
GF
=
BE
、
GF
=
 CF
。这个交点称为三角形的重心,因为它是此三角形的重力中心。这意味着,如果你想保持一块三角形纸板平衡,那么就应该以三角形的重心位置作为支点。
CF
。这个交点称为三角形的重心,因为它是此三角形的重力中心。这意味着,如果你想保持一块三角形纸板平衡,那么就应该以三角形的重心位置作为支点。
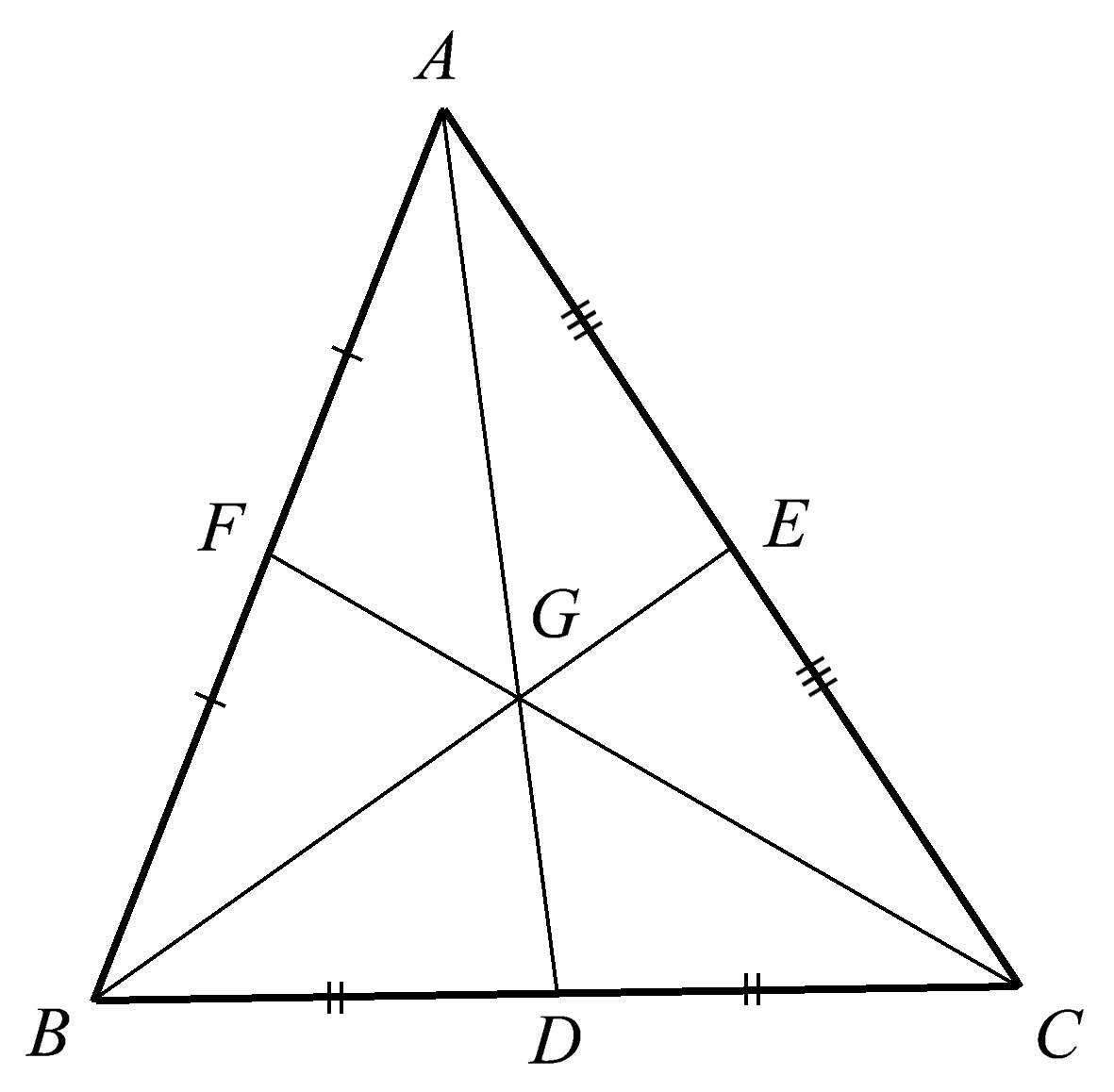
图1.17
此外,如图1.17,三条中线将三角形 ABC 分割为六个面积相等的小三角形。
直线的共点性有时在我们最意想不到的时候出现。例如,任意作一条平行于三角形一边的直线,与三角形的两条边相交。将该三角形的两个顶点与上述两个交点相连,这两条连线的交点总是位于从第三个顶点出发的中线上。如图1.18所示, PQ 与三角形 ABC 的边 BC 平行。令人相当惊讶的是, PC 和 QB 总是与中线 AM 共点。
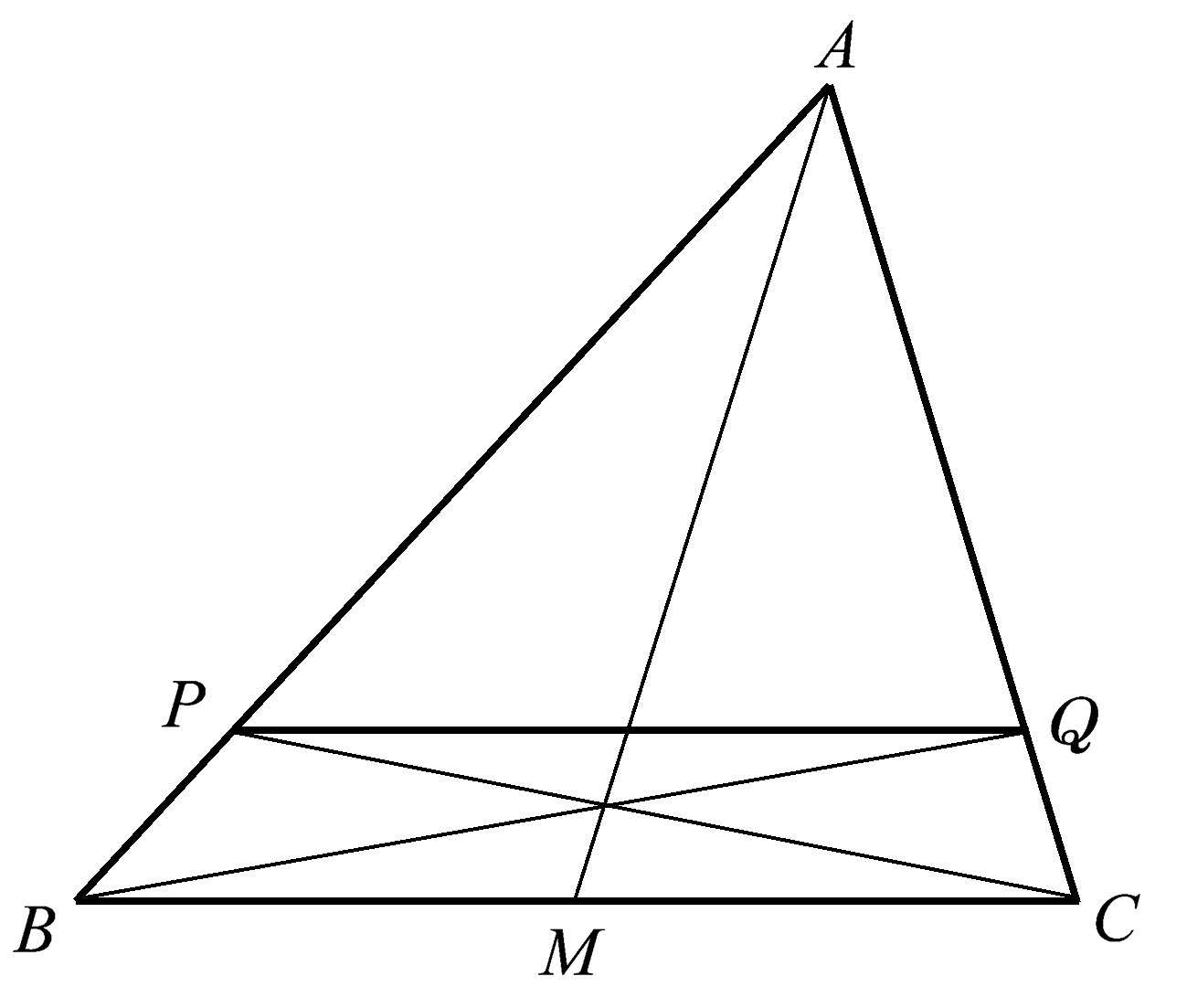
图1.18
如果我们使平行于 BC 边的 PQ 通过 AM 的中点 N ,我们就会发现 N 既是 AM 的中点,也是 PQ 的中点,如图1.19所示。请注意,当两条线段(比如 AM 和 PQ )彼此平分时,它们就构成了平行四边形 AQMP 。
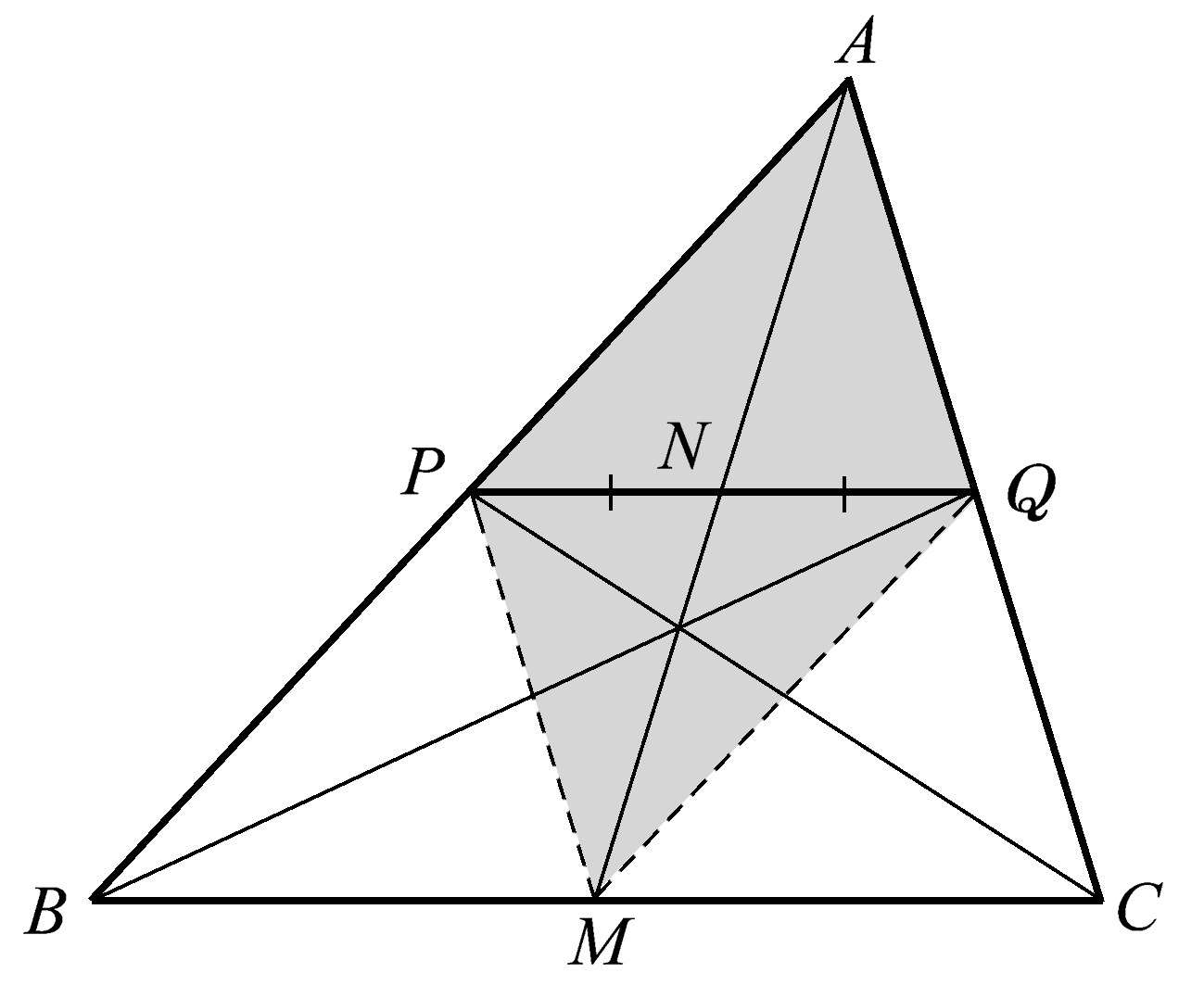
图1.19
1678年,意大利数学家塞瓦(Giovanni Ceva,1648—1734)在他的著作《直线论》( De lineis rectis )中发表了一条关于三角形中的直线共点的定理,这条定理极为有用,但常常被忽视。早在11世纪,阿拉伯数学家胡德(Al-Mu’taman ibn Hūd)就已经证明了这条定理,尽管如此,我们仍然把它归功于塞瓦,因为人们在塞瓦发现该定理前,对它一无所知。这条定理指出,连接三角形各顶点与对边的三条线段,当且仅当由它们与对边的交点所确定的沿各边的交替线段乘积相等时,这三条线段共点。在图1.20中,当且仅当 AF·BD·CE = FB·DC·EA 时, AD 、 BE 、 CF 这三条直线共点。利用塞瓦定理,证明三角形的中线共点会变得十分简单,因为此时交替线段的乘积显然相等。塞瓦定理在建立连接顶点与三角形对边的线段的共点性时非常有用,我们将在后文中看到。
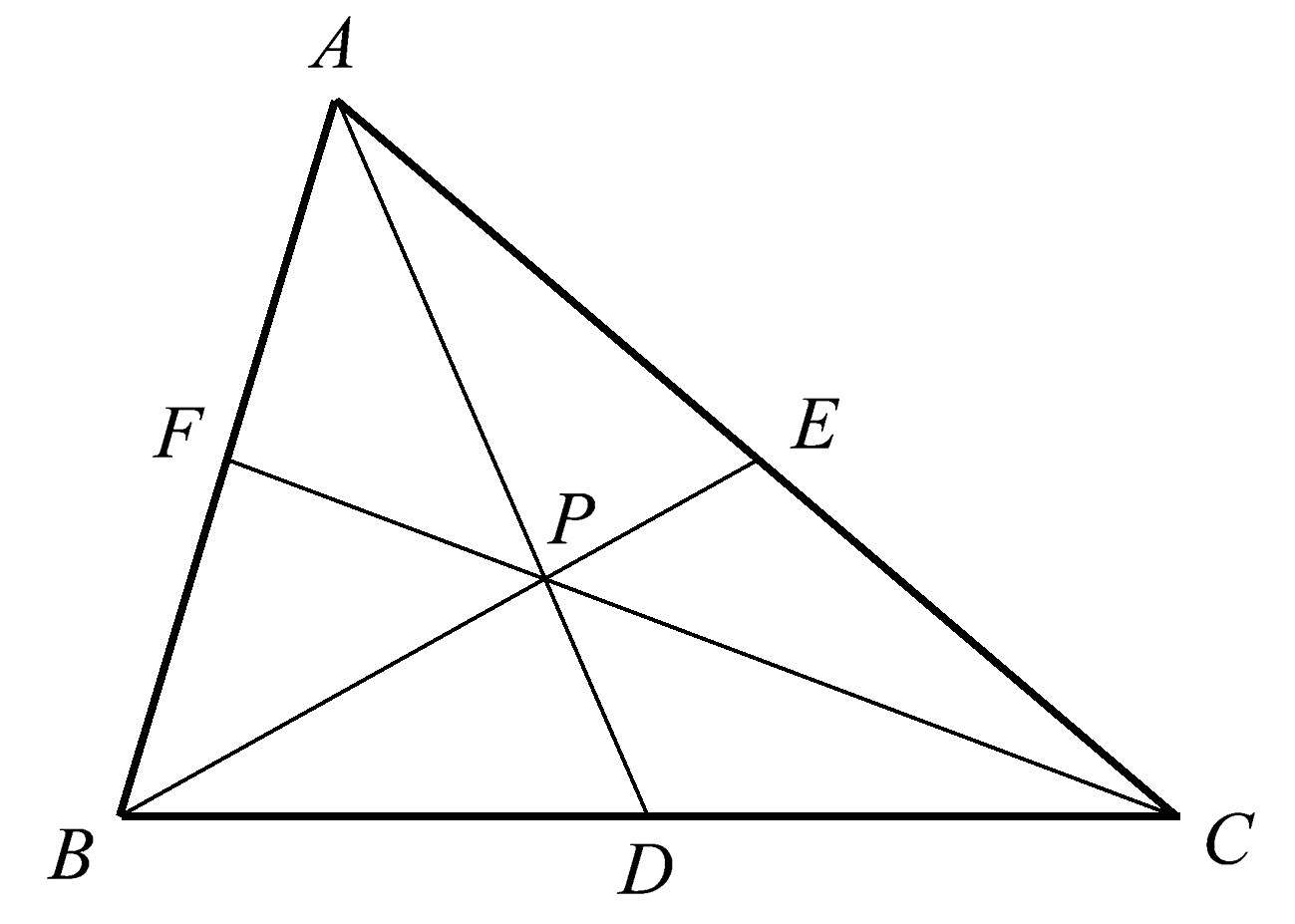
图1.20
另一个应该在高中几何中介绍的共点性是一个三角形的三条角平分线的共点性。图1.21展示了角平分线 AD 、 BE 、 CF 的共点性,它们相交于点 I 。该点称为内心,因为它是三角形内切圆(即与三角形三条边都相切的圆)的圆心。
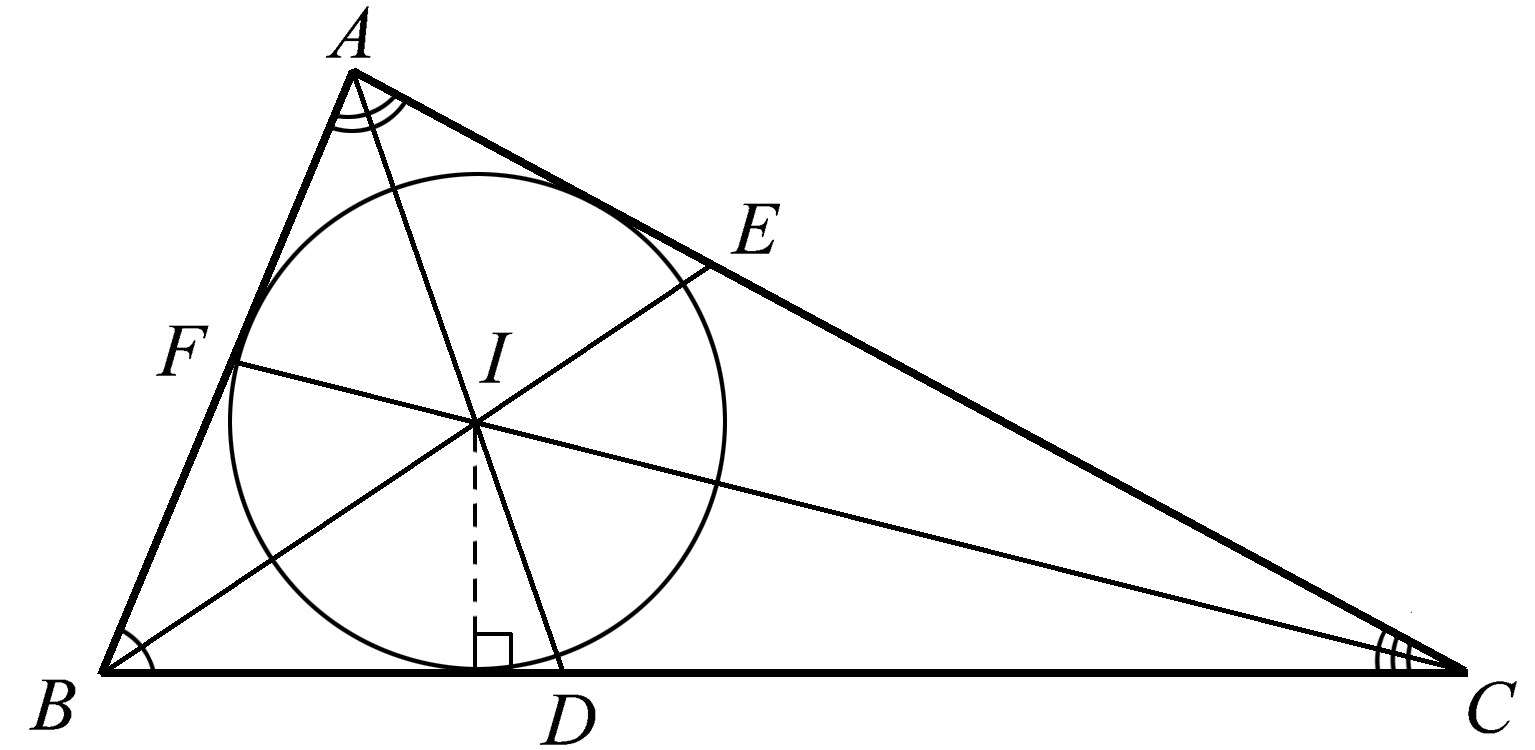
图1.21
塞瓦定理在证明三角形的三条角平分线共点性时非常有用。塞瓦定理还能证明一个三角形的一条内角平分线与其他两个角的外角平分线是共点的,如图1.22所示。延长内角平分线 AL ,它将与两条外角平分线 KB 和 NC 的延长线相交于点 P 。志存高远的读者可以尝试用塞瓦定理来证明这种共点性。我们在这里只是欣赏这样一个事实:平面几何之中存在着诸如此类的一些迷人关系。

图1.22
三角形的角平分线会衍生出许多不同寻常的共点性。我们将在这里展示其中之一作为例子,在后文中还将展示其他例子。在图1.23中, AD 是∠ BAC 的平分线,点 M 和点 N 分别是内切圆与三角形的 AC 边和 BC 边的切点。 MN 与 AD 的交点是点 P 。有趣的是,当我们从点 B 向 AD 作垂线时,垂足恰好是点 P 。
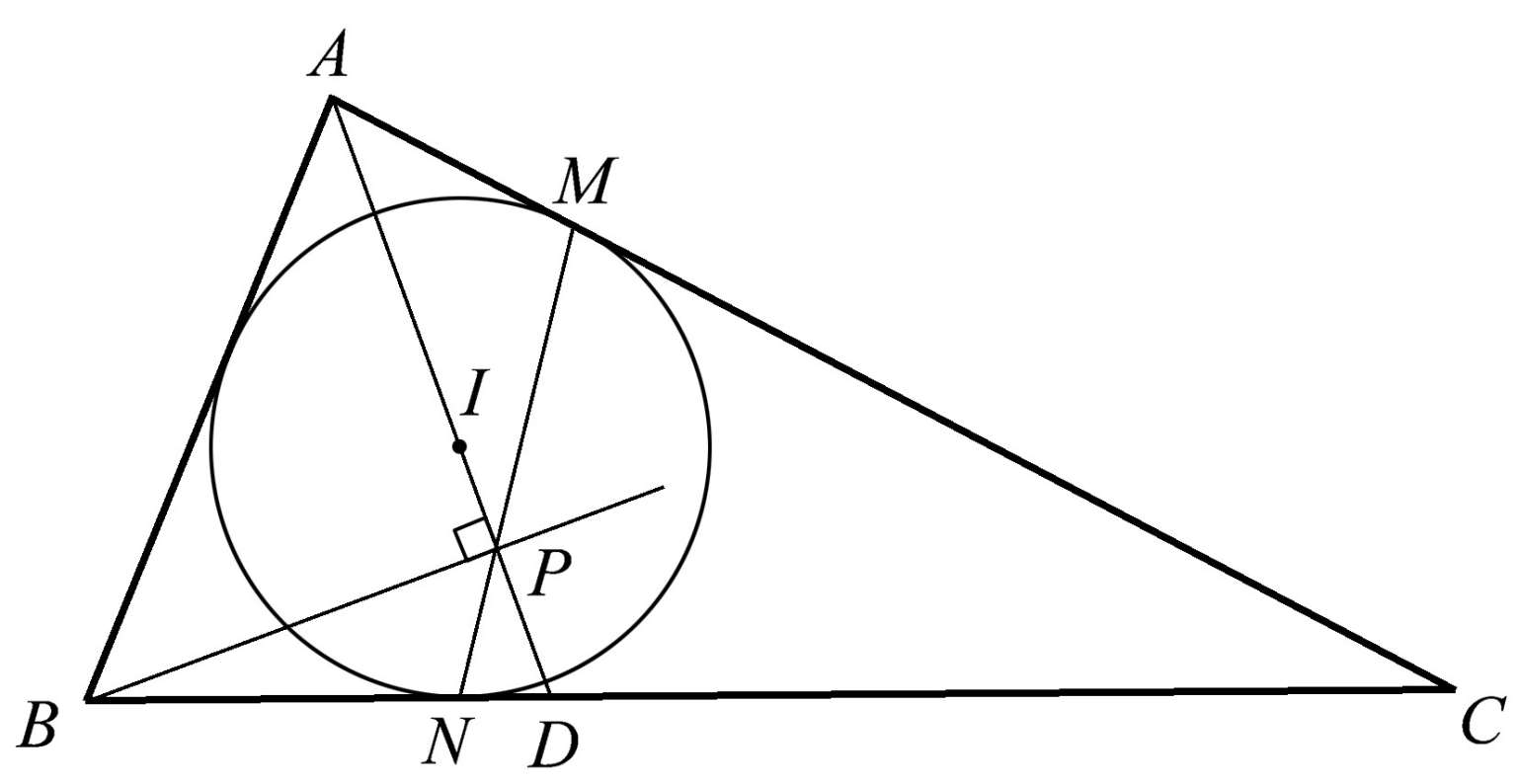
图1.23
另一个共点的例子同时使用了三角形内切圆和外接圆,如图1.24所示。有一个三角形 ABC ,∠ BAC 的平分线是 AD 。过点 D 作一条与 BC 边垂直的直线,它与外接圆的直径 AO 相交于点 P 。相当出乎意料的是, AD 的垂直平分线也过点 P 。
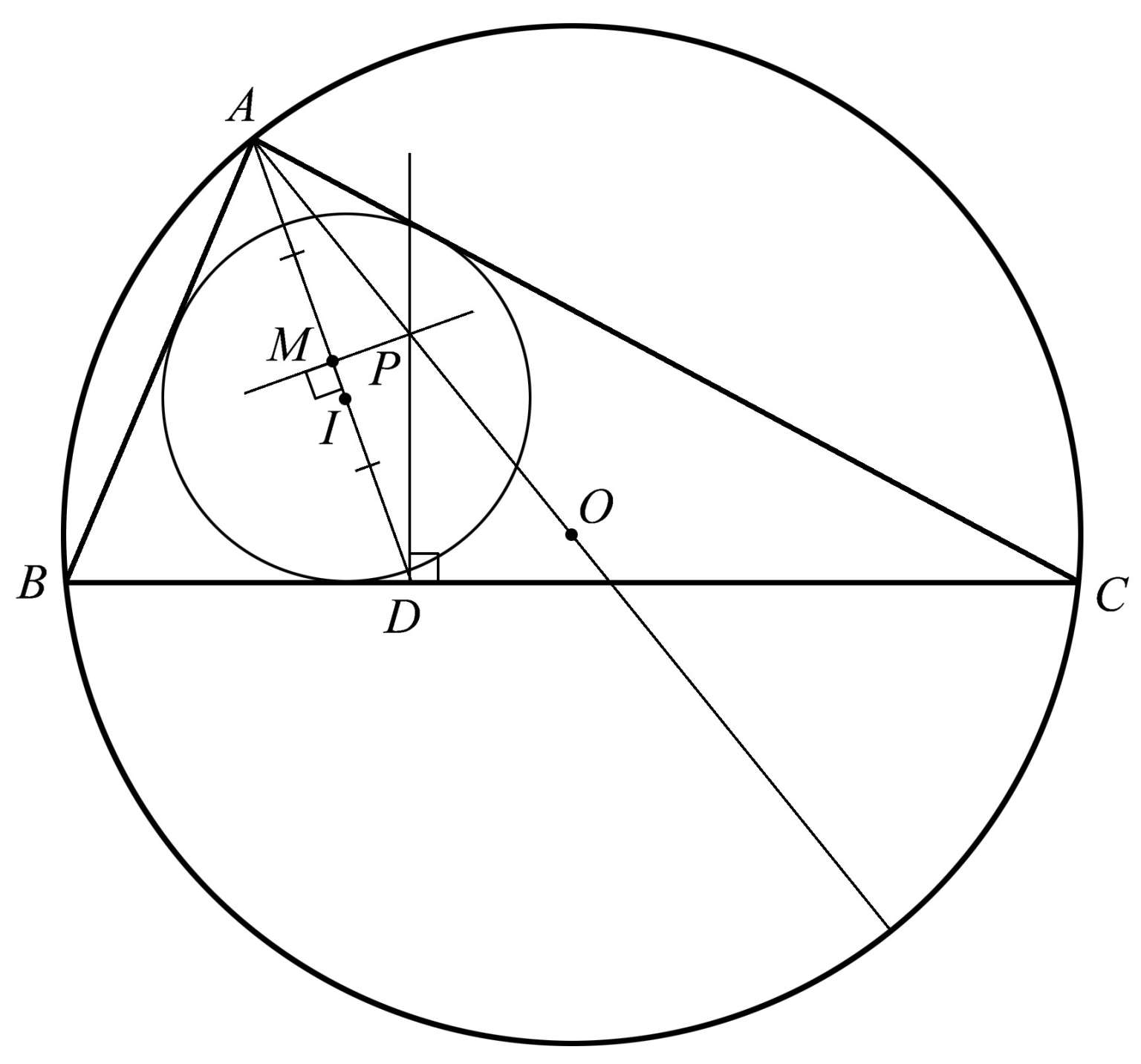
图1.24
在这里,我们来阐明如何从一个任意三角形的一组中点衍生出一些几何关系。在三角形 ABC (图1.25)中,从各个顶点向各条对边作一组共点线 AL 、 BM 、 CN ,这三条线段的中点分别是 P 、 Q 、 R 。这个三角形的三条边的中点是 D 、 E 、 F 。

图1.25
然后我们作三角形 DEF (图1.26),它的各边与三角形 ABC 的对应边平行。显然,当你把一个三角形的两边中点连起来时,这样构成的线段长度是第三条边的一半,并且平行于第三条边。但现在我们要寻找另一组共点线。
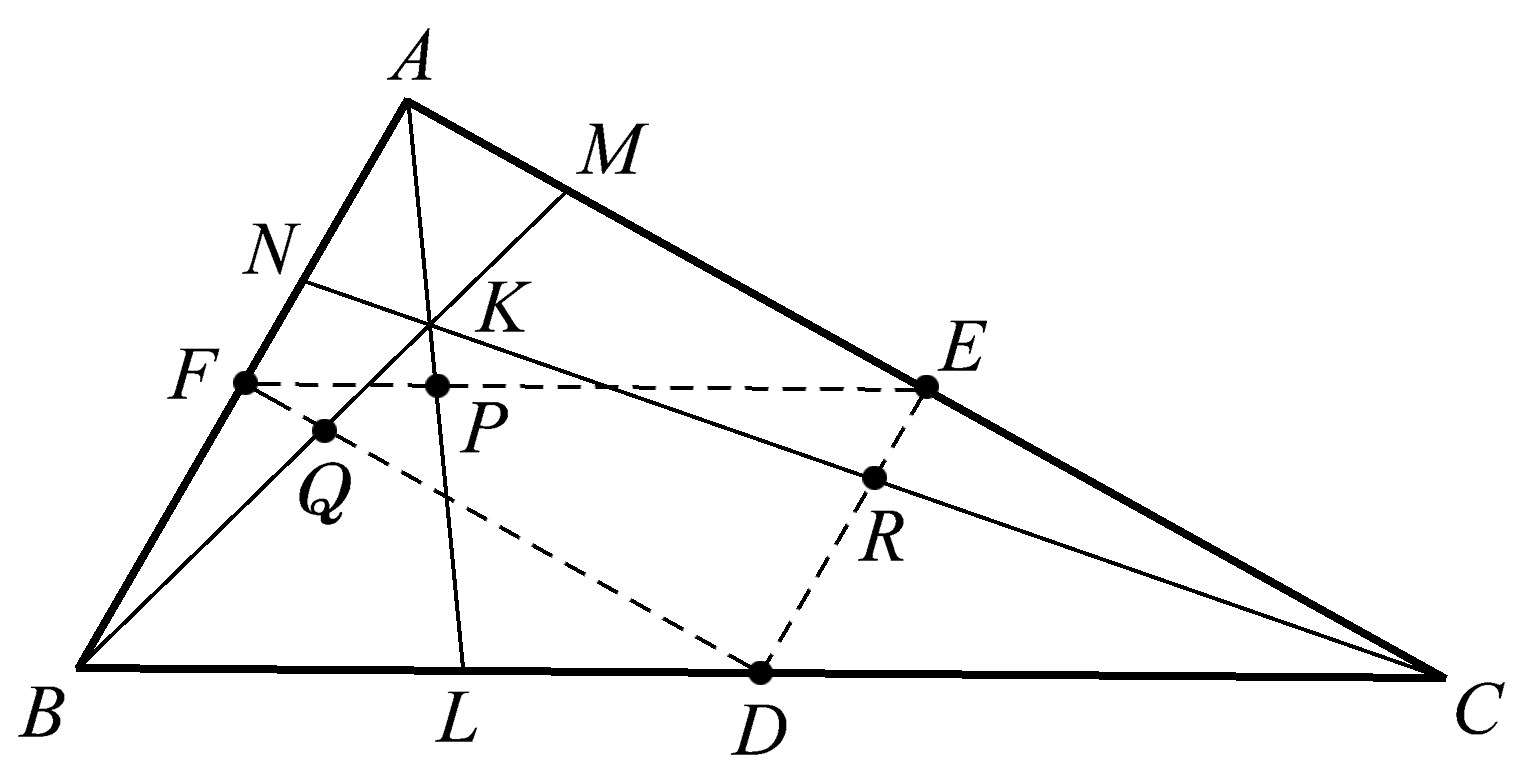
图1.26
假设我们将三角形 ABC 的各边中点分别与 AL 、 BM 、 CN 的三个中点(即 P 、 Q 、 R )连接起来。我们意外地得到了另一组共点线, PD 、 QE 、 RF ,它们都过点 S ,如图1.27所示。
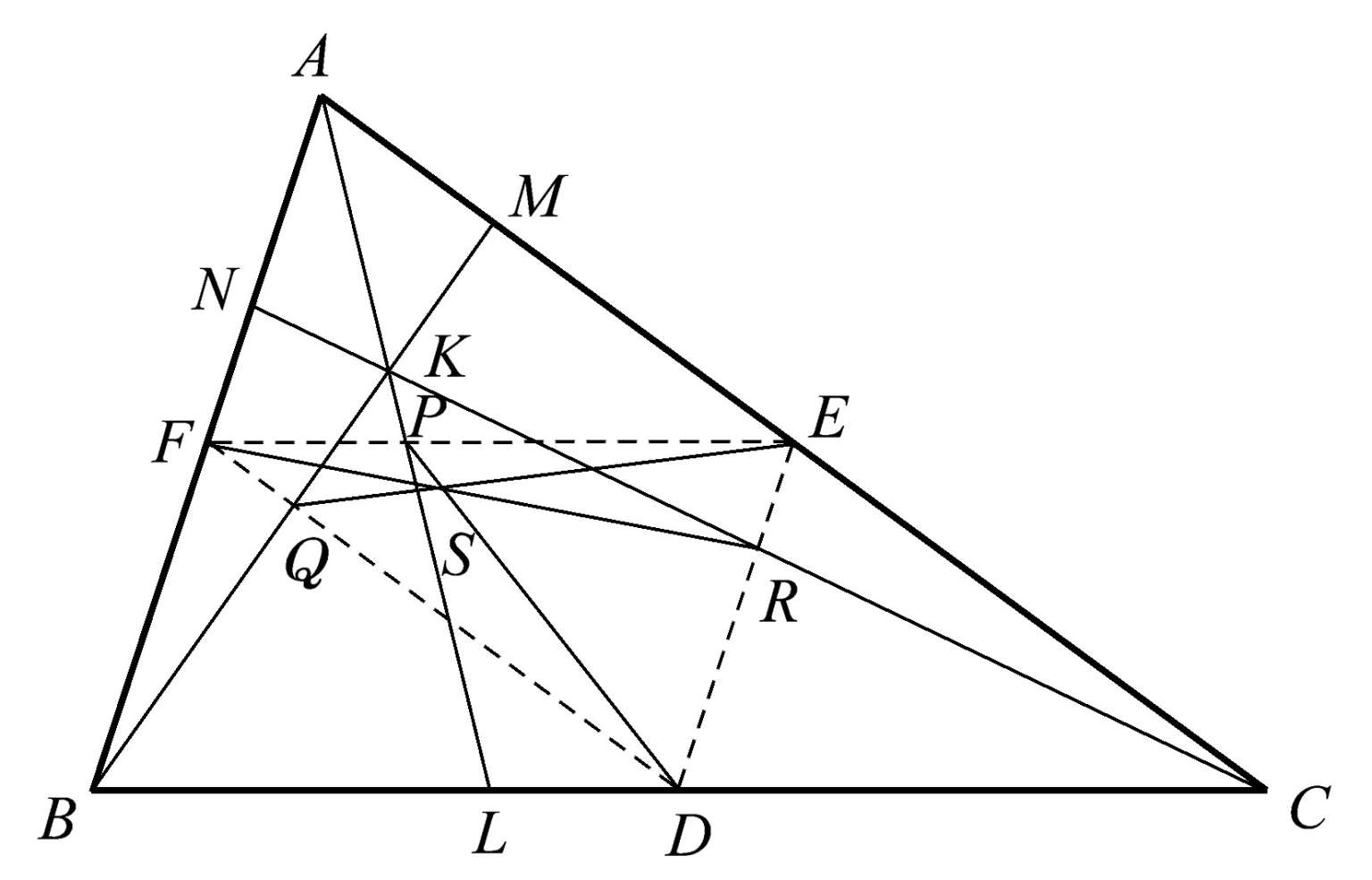
图1.27
正如我们刚才所看到的,共点性可以衍生出其他共点性。甚至也许可以源源不断地找到更多这样的关系。我们只需选择三角形 ABC 内的任意点 P ,并将其与每个顶点相连,如图1.28所示。就得到了三条共点线段 AP 、 BP 、 CP 。然后作顶点 P 处的每个角的角平分线。这样就得到∠ APB 的平分线 PF 、∠ APC 的平分线 PE 、∠ BPC 的平分线 PD ,其中的点 D 、 E 、 F 都在三角形 ABC 的各边上。当我们连接 AD 、 BE 、 CF 时,就会发现它们是共点的。
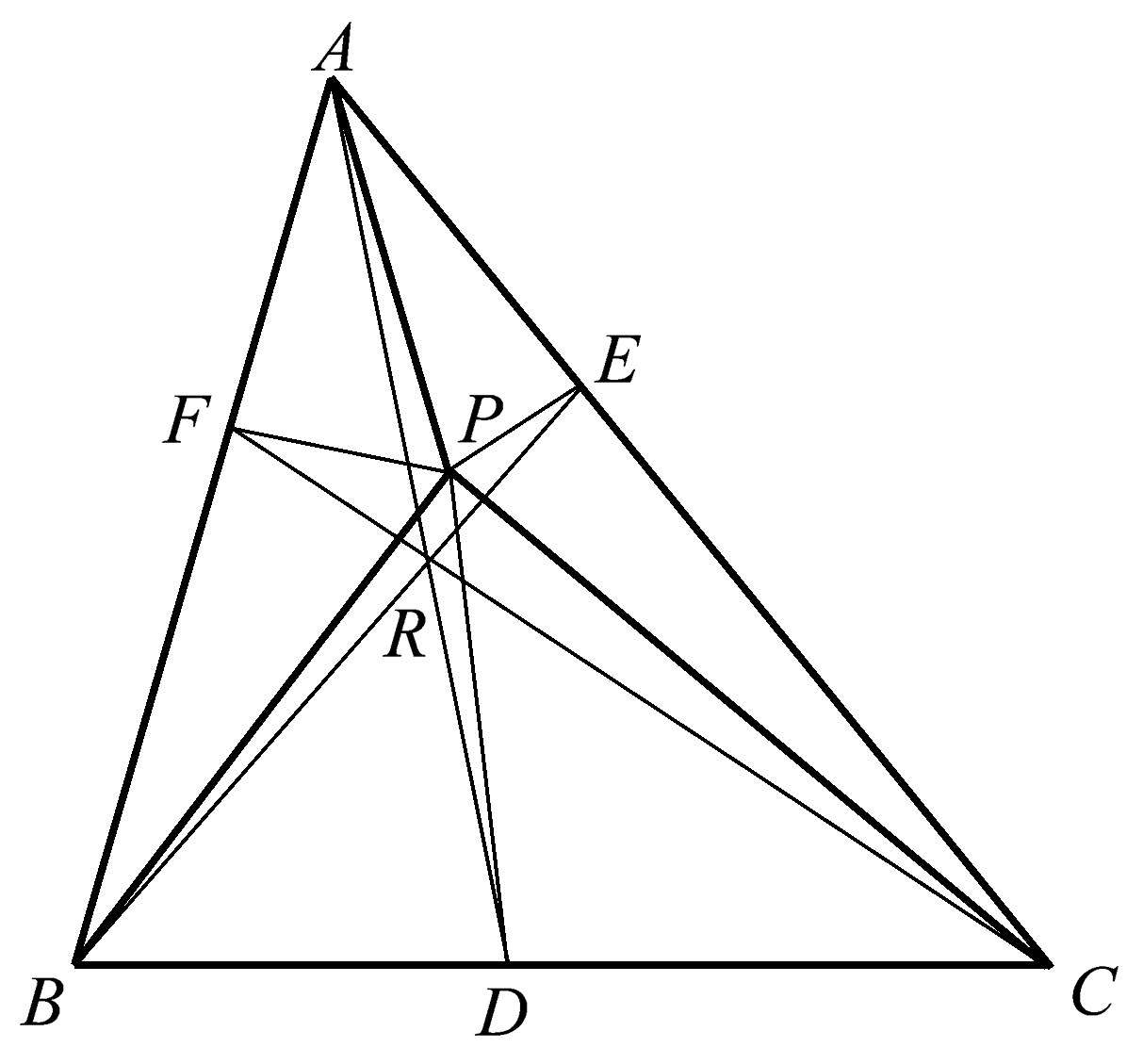
图1.28
我们也可以在三角形内随机选择一些共点线。如图1.29所示,在三角形 ABC 内选择一个随机点 P 。然后我们分别找到三角形 ABC 各边 AB 、 BC 、 CA 的中点 M 、 K 、 N 。当我们分别通过点 K 、 N 、 M 作平行于 AP 、 BP 、 CP 的直线 KL 、 NJ 、 MG 时,我们发现它们共点于点 Q 。请回忆一下,点 P 是随机选择的,因此无论点 P 位于三角形 ABC 中的什么位置,这些直线都有公共点 Q 。
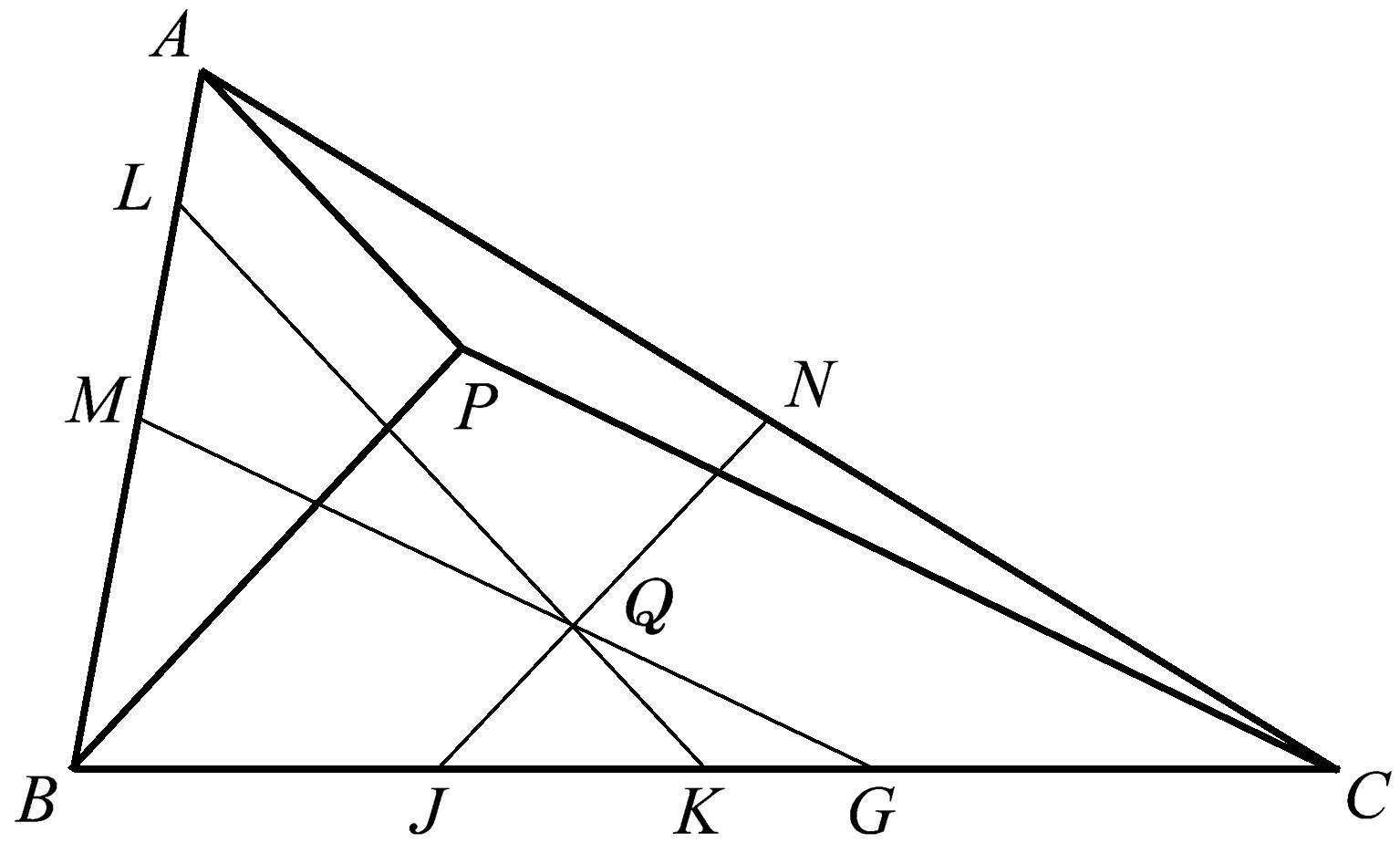
图1.29
有时一个共点性可以衍生出另一个共点性。在这里,我们要展示一种非同寻常的相关共点性。我们从三角形 ABC 开始,如图1.30所示,在此三角形中自顶点 A 、 B 、 C 作任意三条共点线 AP 、 BP 、 CP 。然后作三角形 DEF ,使其每一边分别垂直于上述三条共点线。在图1.30中, DE 垂直于 AP , DF 垂直于 BP , EF 垂直于 CP 。接下来从三角形 DEF 的各顶点分别向三角形 ABC 的三边作垂线。在这里,我们看到 DK 垂直于 AB , EL 垂直于 AC , FM 垂直于 BC 。出乎意料的是,当延长这三条垂线时,我们发现 DQ 、 EQ 、 FQ 共点于点 Q 。虽然我们花了一点时间才找到这种共点性,但它进一步展示了几何学所特有的值得探索的图案。
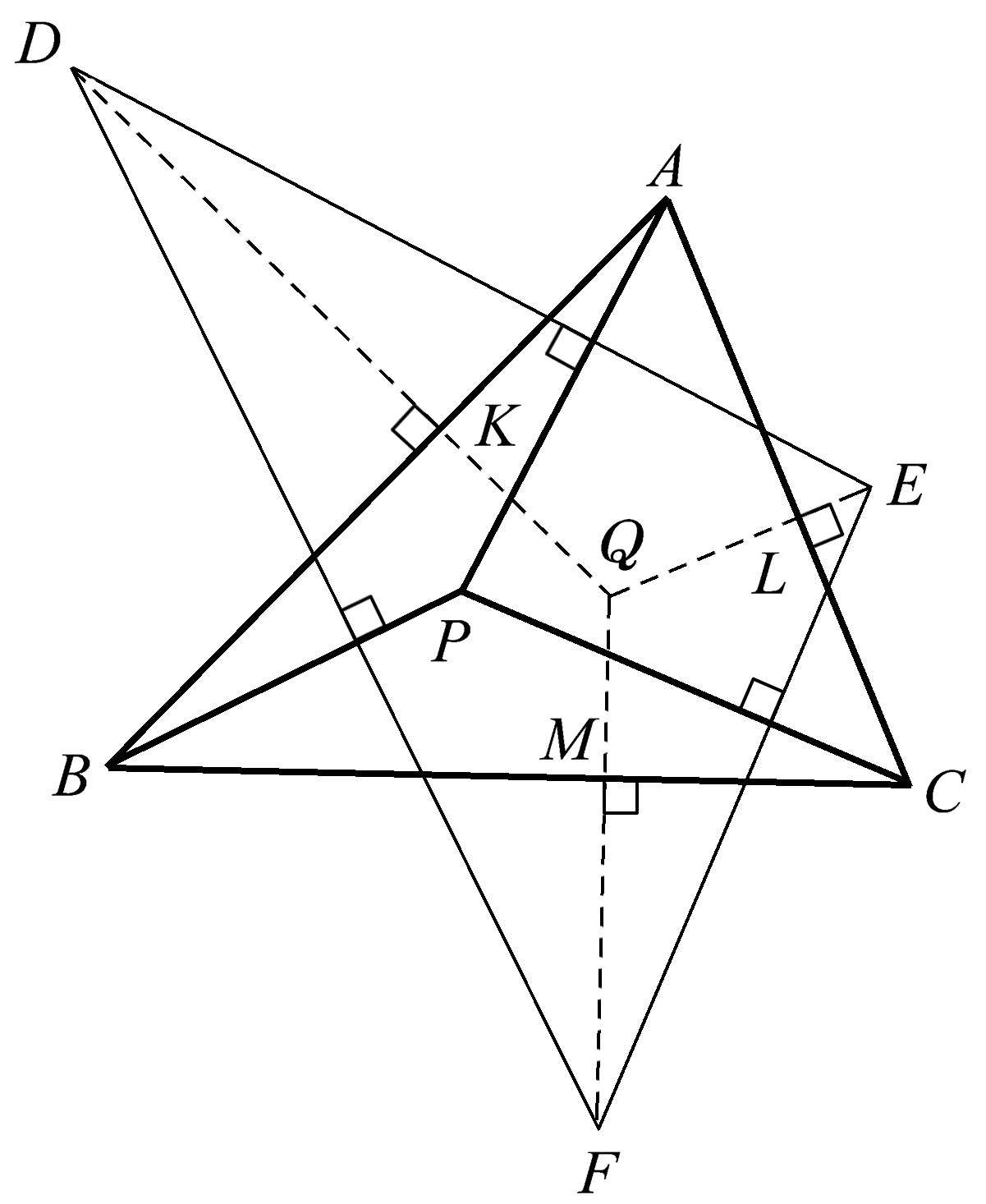
图1.30
有时,我们可以构造出一个具有惊人意义的共点。如图1.31中的三角形 ABC ,用点 D 和点 E 将边 BC 三等分。这相当于将三角形 ABC 也三等分了,即三角形 ABD 、 ADE 、 AEC 都具有相同的面积。这一点很容易看出来,因为这三个三角形的底都是相等的,而且从 A 到直线 BC 的高也相同。我们运用共点性以另一种方式把这个三角形三等分。方法如下:作直线 DF 平行于 AB ,直线 EJ 平行于 AC 。 EJ 与 DF 相交于点 P ,通过这个点便可以将这个三角形分为面积相等的三块,即三角形 APB 、 APC 、 BPC 。我们在前面遇到过类似的情况(图1.17),当时我们注意到,三角形的三条中线将三角形分为六个面积相等的小三角形。因此,如果我们将那些三角形两两组合,就可以将原三角形分为三个面积相等的小三角形。
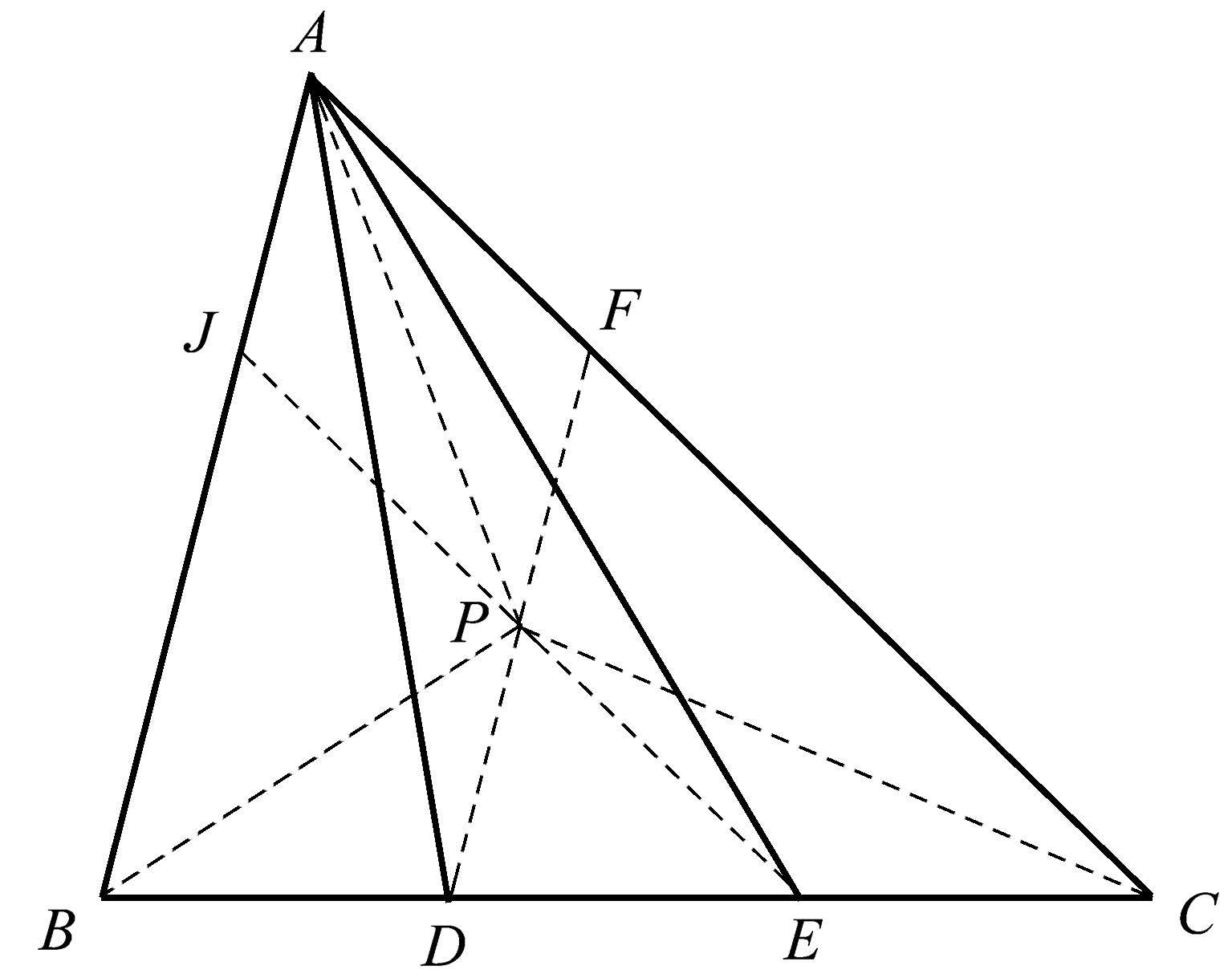
图1.31
现在我们在研究直线共点性的同时引入与三角形相关的圆。其中包括内切圆、外接圆,以及与三角形边相交于六个不同点的一些圆。
让我们首先考虑一个由三角形的内切圆衍生而来的共点性。我们之前已经注意到,三角形内切圆的圆心是三条角平分线的交点。如图1.32所示, AD 、 BE 、 CF 是三条角平分线,它们共点于点 I 。借助内切圆,就可以得到另一组三线共点。将三角形的各顶点与内切圆的切点 T 、 U 、 V 连接起来,就得到了直线 AT 、 BU 、 CV ,它们共点于点 K 。这一点被称为热尔岗点,这是以它的发现者法国数学家热尔岗(Joseph Diaz Gergonne, 1771—1859)的名字命名的。
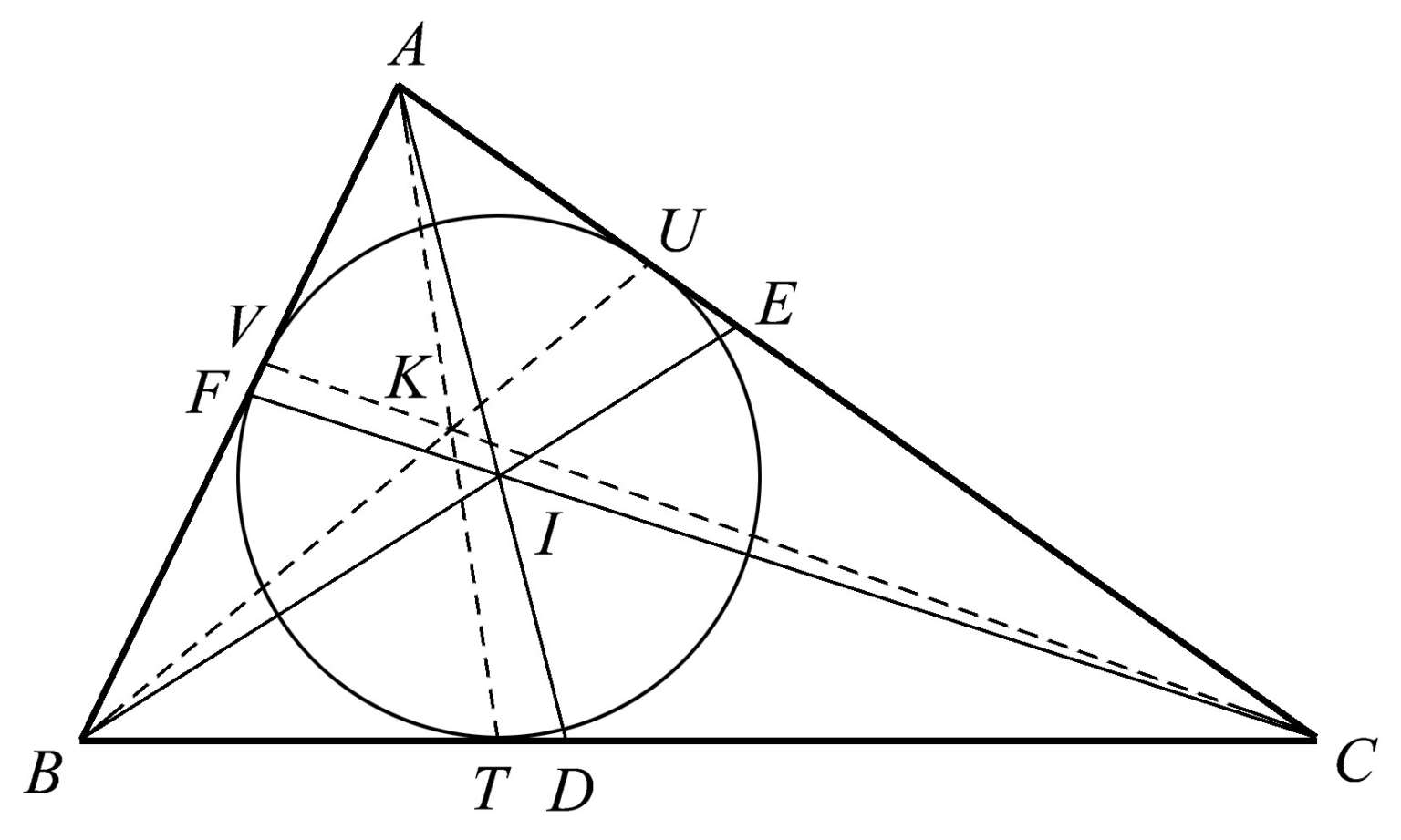
图1.32
三角形的内切圆还能衍生出其他几种神奇的共点性。其中一些可能看起来有些不自然,而我们将讨论另外两种共点性,希望以此激励读者去寻找更多这样的关系。
在图1.33中,我们作三角形的内切圆,再过其切点 T 、 U 、 V 作直径,分别与内切圆相交于点 M 、 N 、 Q 。然后我们将三角形的每个顶点与这些交点连接起来,得到 AM 、 BN 、 CQ 。延长它们,它们将神奇地共点于点 P 。这种关系的特殊之处在于它并不广为人知,而且适用于所有三角形。
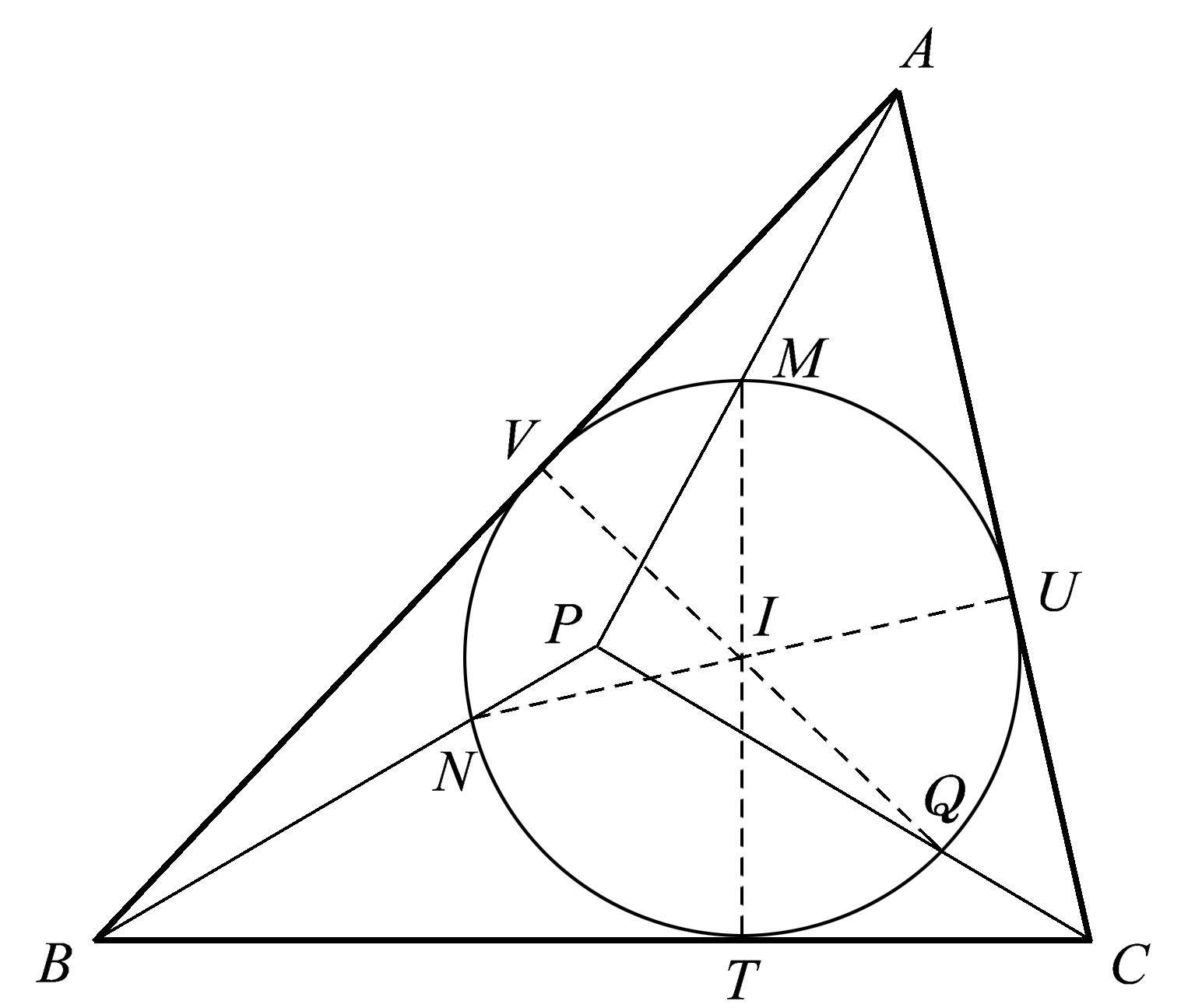
图1.33
我们现在进行一个类似的作图。首先作任意三条共点线(公共点 R )。但这一次,它们不经过内切圆的圆心,它们分别从三个切点( T 、 U 、 V )出发,与圆的另一侧相交于点 W 、 Y 、 Z ,如图1.34所示。将这些新确定的点 W 、 Y 、 Z 分别与最近的顶点相连,我们就再次发现了另一个共点性: AW 、 BY 、 CZ 的延长线相交于点 L 。

图1.34
有时候,看起来错综复杂的图可能会给出一个相当出乎意料的共点性。如图1.35所示的三角形 ABC ,其中高 AY 、 BZ 、 CX 相交于点 Q ,即垂心。借助此三角形任意两条边的垂直平分线,可以很容易确定其外接圆的圆心,即点 P 。然后找出 AP 、 BP 、 CP 的中点 G 、 H 、 K 。神奇的是,我们发现线段 GD 、 HE 、 FK 共点于点 O 。
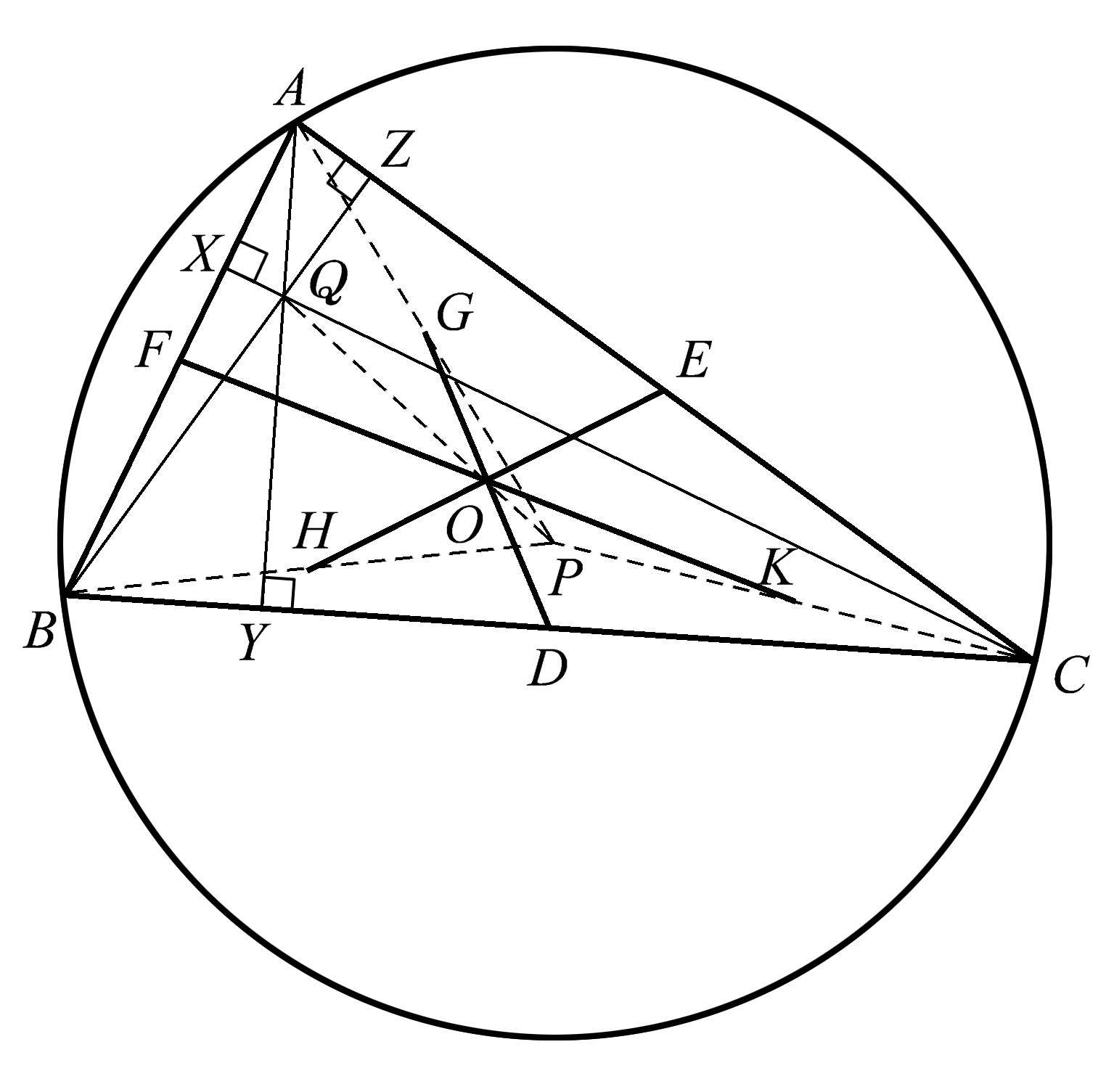
图1.35
另外,也请注意这个构形中的垂心,因为它还有一个神奇之处,即点 Q 、 O 、 P 是共线的。因此,这个图不仅显示了一个共点性,而且还显示了一个共线性。这成为了下一章的铺垫。
在我们寻找另一个共点性时,首先在图1.36中找出垂心与各个顶点的连线的中点,即线段 AQ 、 BQ 、 CQ 的中点 G 、 H 、 K 。然后我们将 G 、 H 、 K 与三角形的三边中点 D 、 E 、 F 相连。又一次,我们惊讶地发现 GD 、 HE 、 FK 是共点的,而且它们具有相同的长度!这是一个相当神奇的关系,在高中几何中却完全被忽视了。
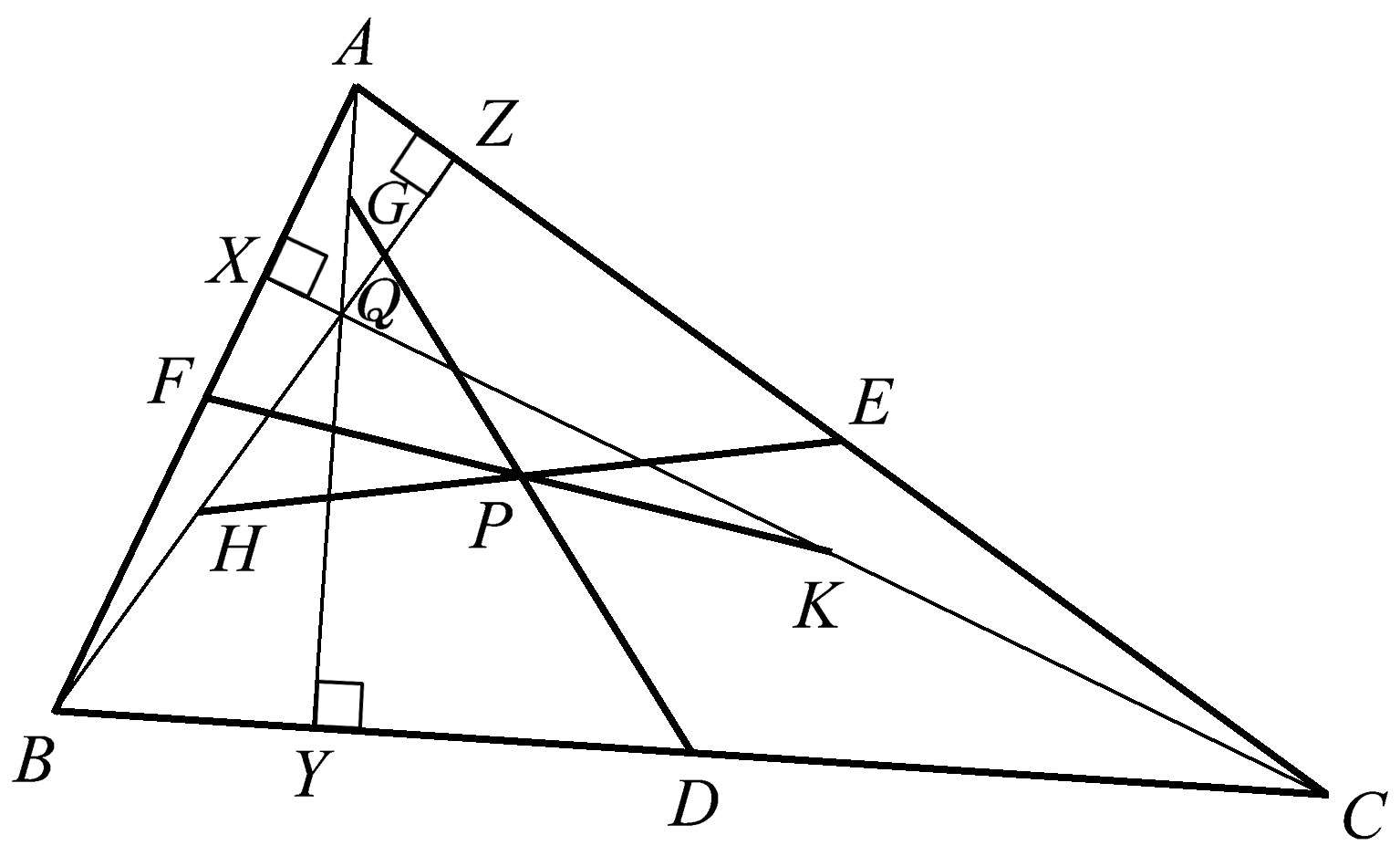
图1.36
在三角形中可以找到无穷多种共点性。我们来讨论两个有同一内切圆的三角形。如图1.37所示,其中三角形 ABC 和 DEF 有一个公共的内切圆,其圆心为 I 。
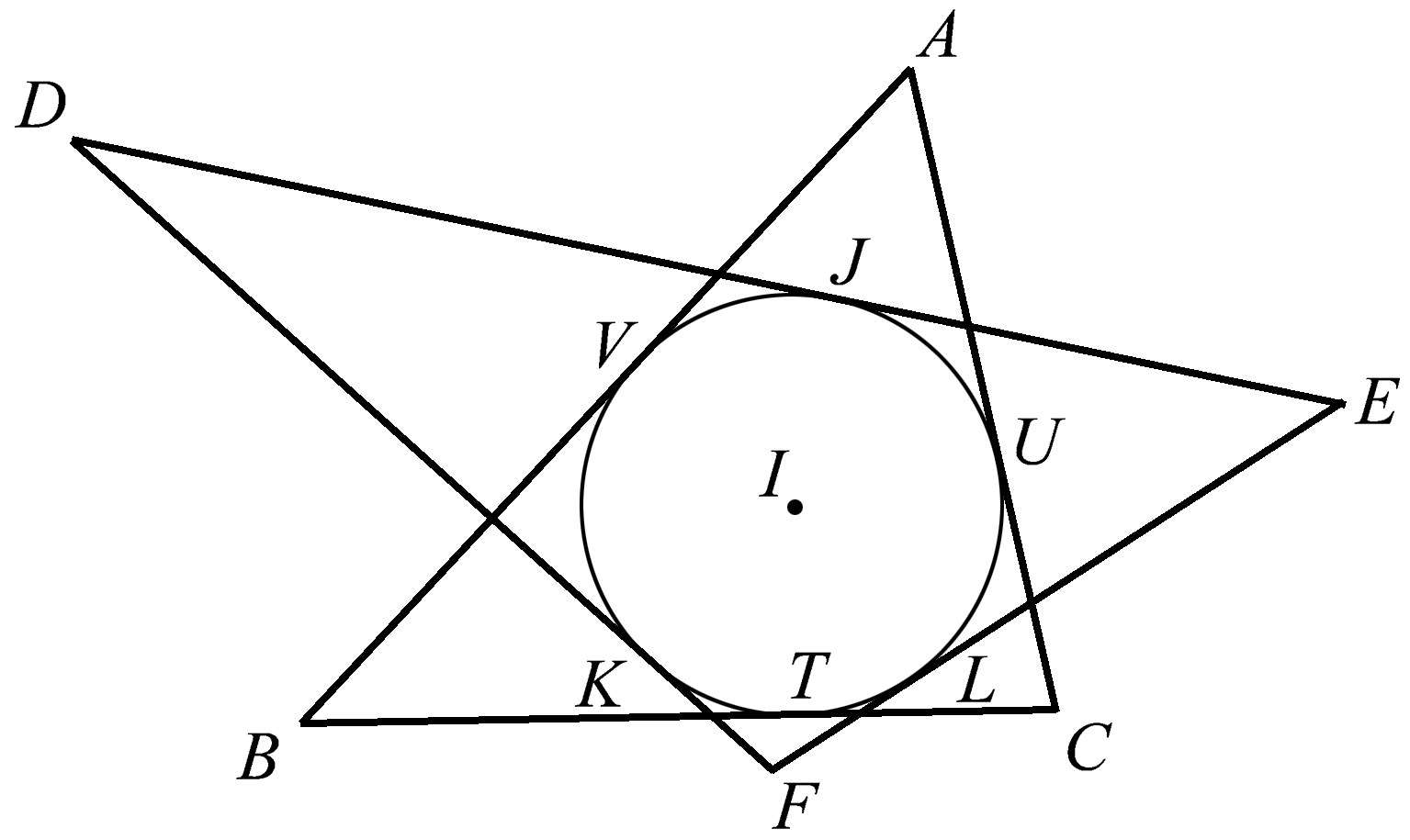
图1.37
不过,还有一个附加条件。这两个三角形的位置应确保其相对顶点的连线 AF 、 BE 、 DC 共点于点 P ,如图1.38所示。
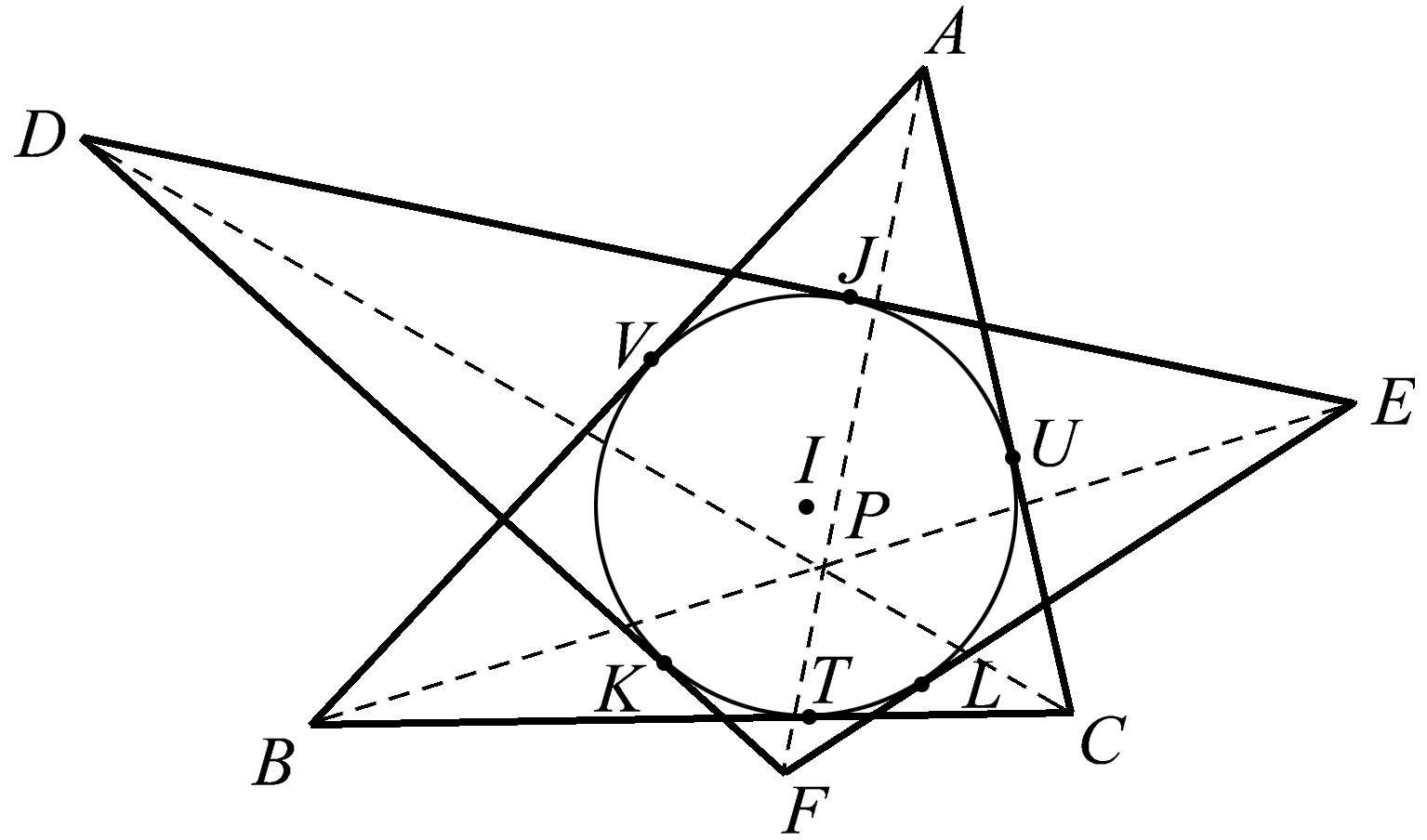
图1.38
神奇的是,当这一条件满足时,各相对切点的连线 TJ 、 UK 、 VL 也共点,如图1.39所示。另一个神奇之处是,这些追加的直线与前三条直线都相交于同一点,即 P 点。这真是太难以置信了!
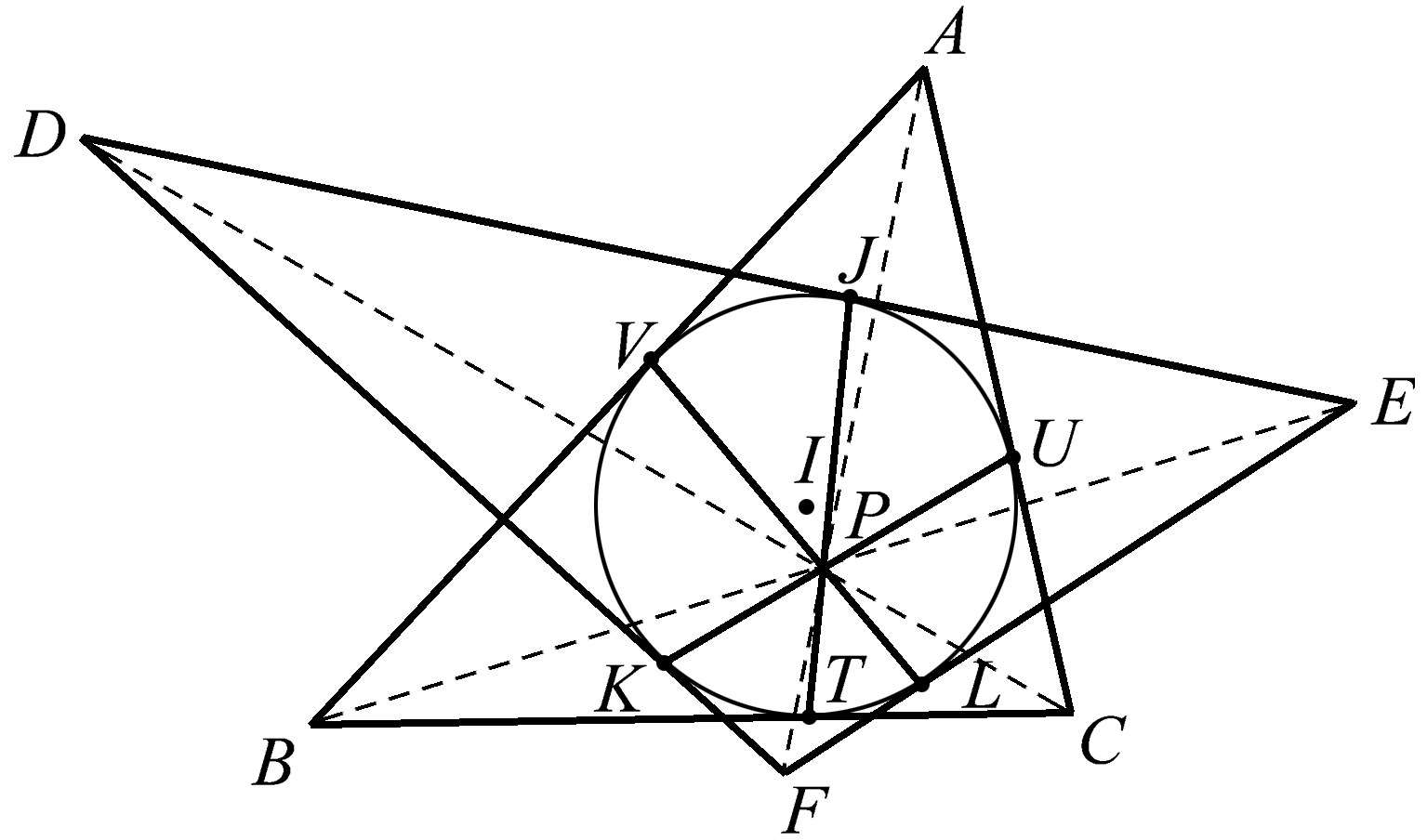
图1.39
有时候,线段的长度可以决定共点性。图1.40中所示的三角形 ABC 就是这样的一个例子,其中点 P 在 BC 边上,且 AB + BP = AC + CP 。同样(虽然在图中没有清楚地表明),点 Q 在 AC 边上,且 BC + CQ = AB + AQ 。此外,点 R 在 AB 边上,且 BC + BR= AC + AR 。当所有这些条件都得到满足时,我们就会非常惊奇地发现, AP 、 BQ 、 CR 共点于点 X 。
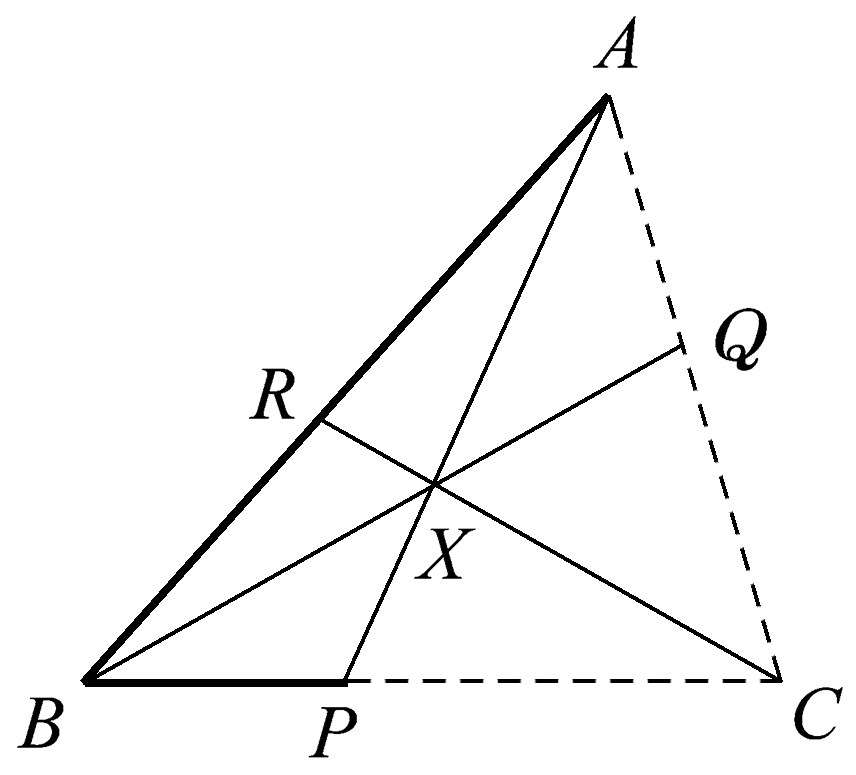
图1.40
当一个共点性出人意料地衍生出另一个似乎完全不相关的共点性时,总是引人遐思。在三角形 ABC 中(图1.41),我们看到有三条随机画出的线 AL 、 BM 、 CN ,它们共点于点 P 。由它们得到三角形 MNL 。然后我们分别找到三角形 MNL 的各边 MN 、 ML 、 NL 的中点 S 、 Q 、 R 。令人相当惊讶的是,线 AS 、 BR 、 CQ (均延长)也是共点的,它们的公共点是点 X 。
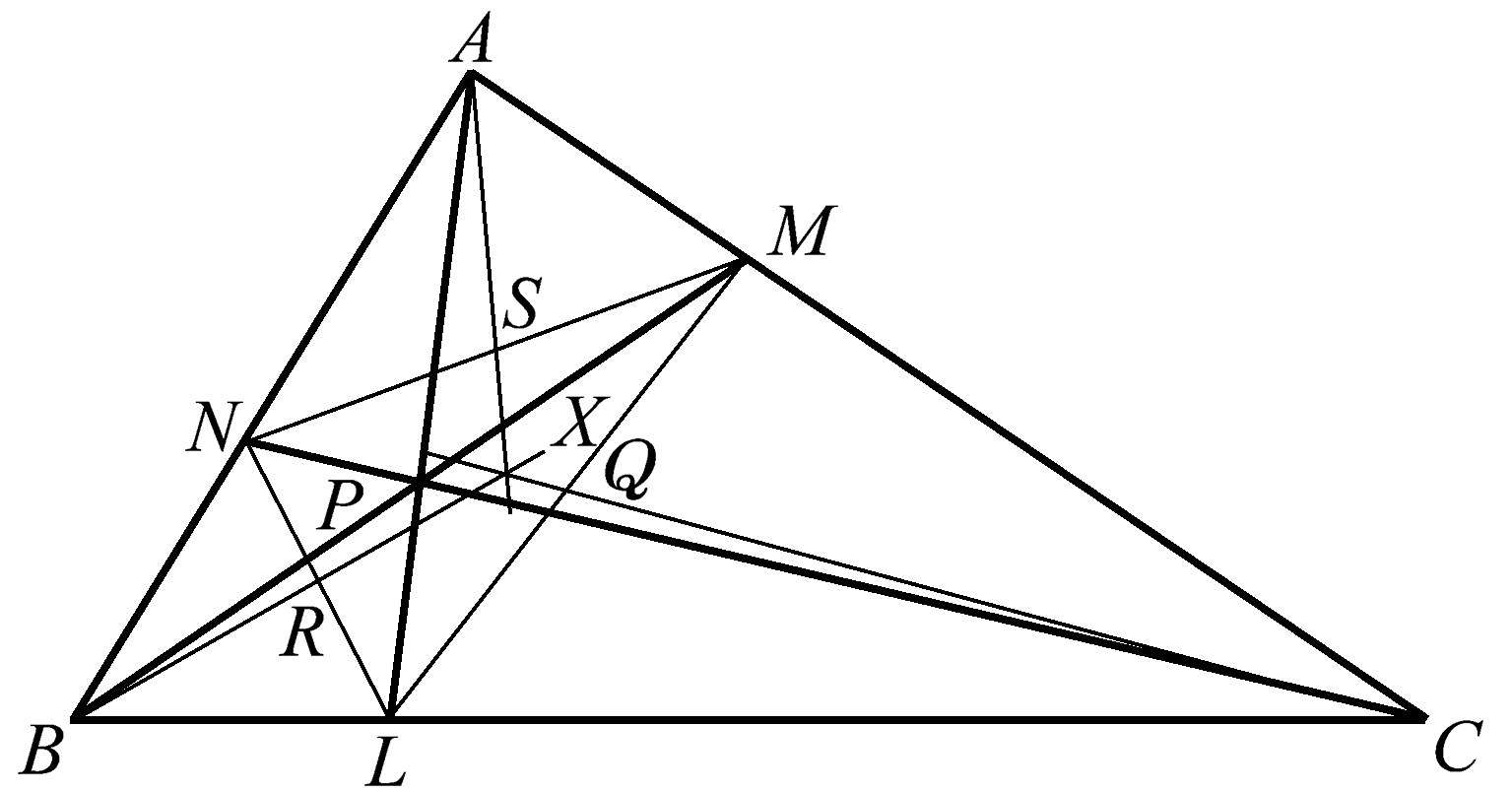
图1.41
前一个例子有一种有趣的变形。我们不使用三角形 MNL 的各边中点,而只选择三角形 MNL 的各边上的其他点 S 、 R 、 Q ,使得 LS 、 MR 、 NQ 共点于点 T ,如图1.42所示。这将使得线 AS 、 BR 、 CQ 也共点于点 K 。请记住,前提是三角形 MNL 应保持在点 P 处有共点性。
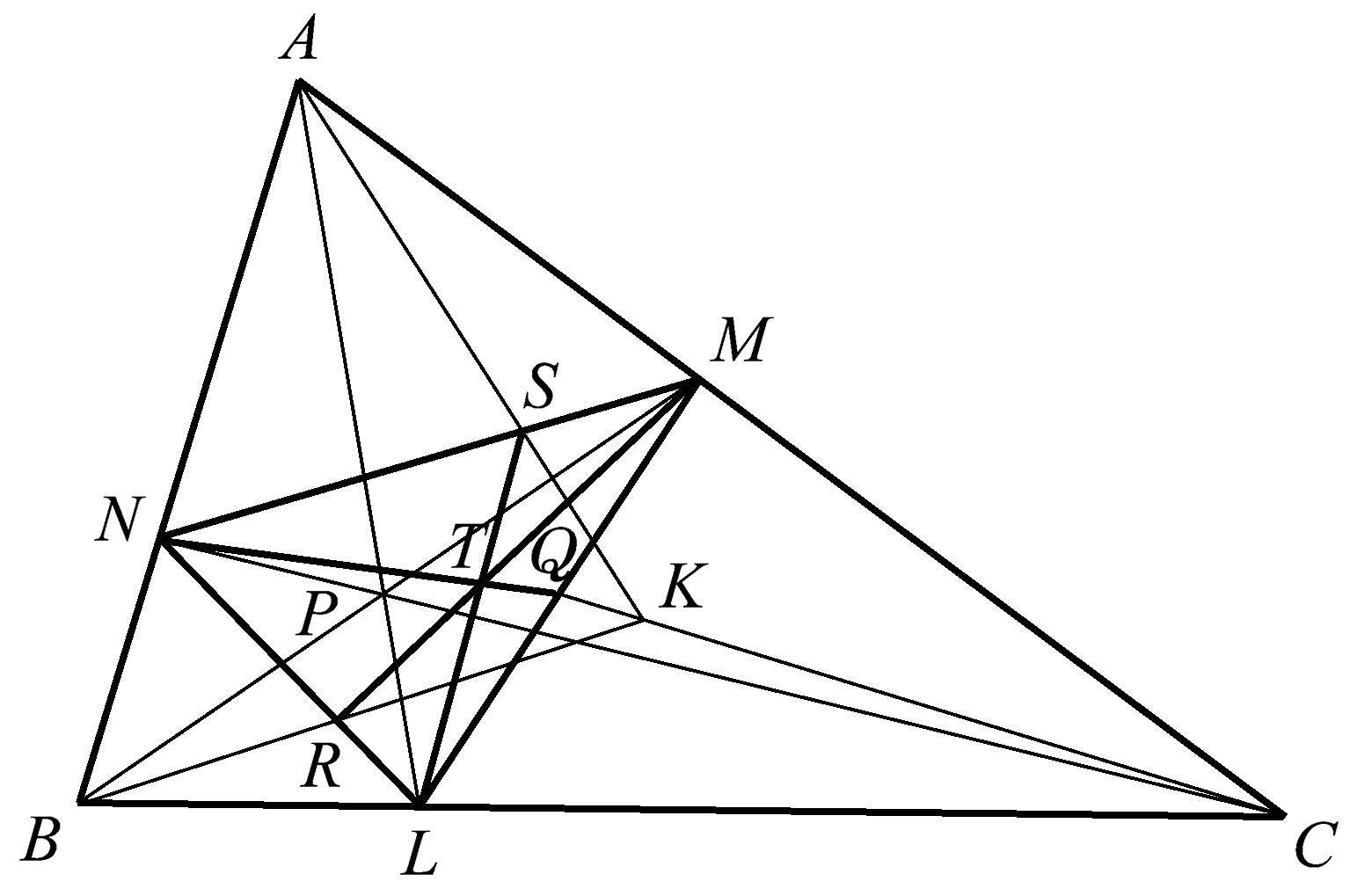
图1.42
接下来的几何关系将令你对几何学叹为观止。一个圆与一个任意三角形相交于六个点,如图1.43所示。注意并不是在三角形中随意画一个相交的圆,而要使线段 AD 、 BF 、 CE 共点于点 P 。(当你尝试作这个圆时,应该首先作三条共点的直线,然后作一个圆,使其过它们与三角形各边的三个交点。)
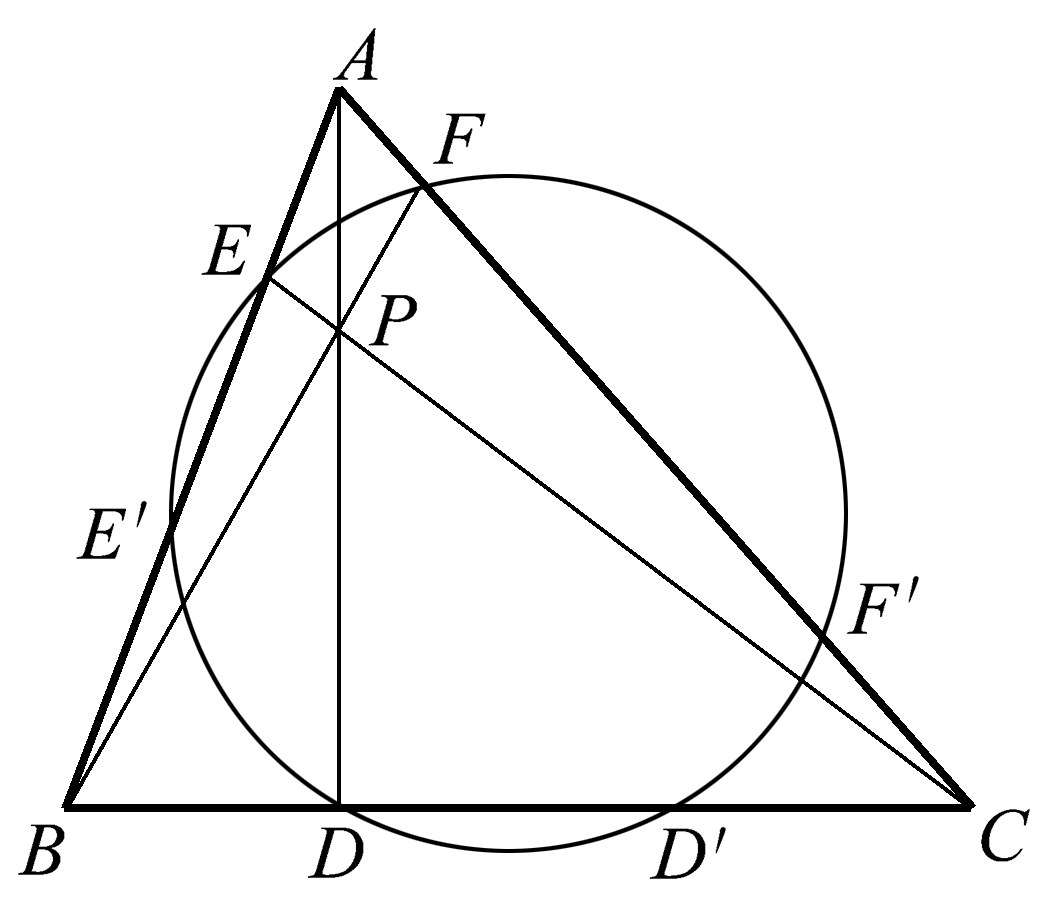
图1.43
令人惊叹的是,如果把三角形 ABC 与圆的另外三个交点 D′ 、 E′ 、 F′ ,与 A 、 B 、 C 分别连接起来,那么你会发现 AD′ 、 BF′ 、 CE′ 共点于点 R ,如图1.44所示。
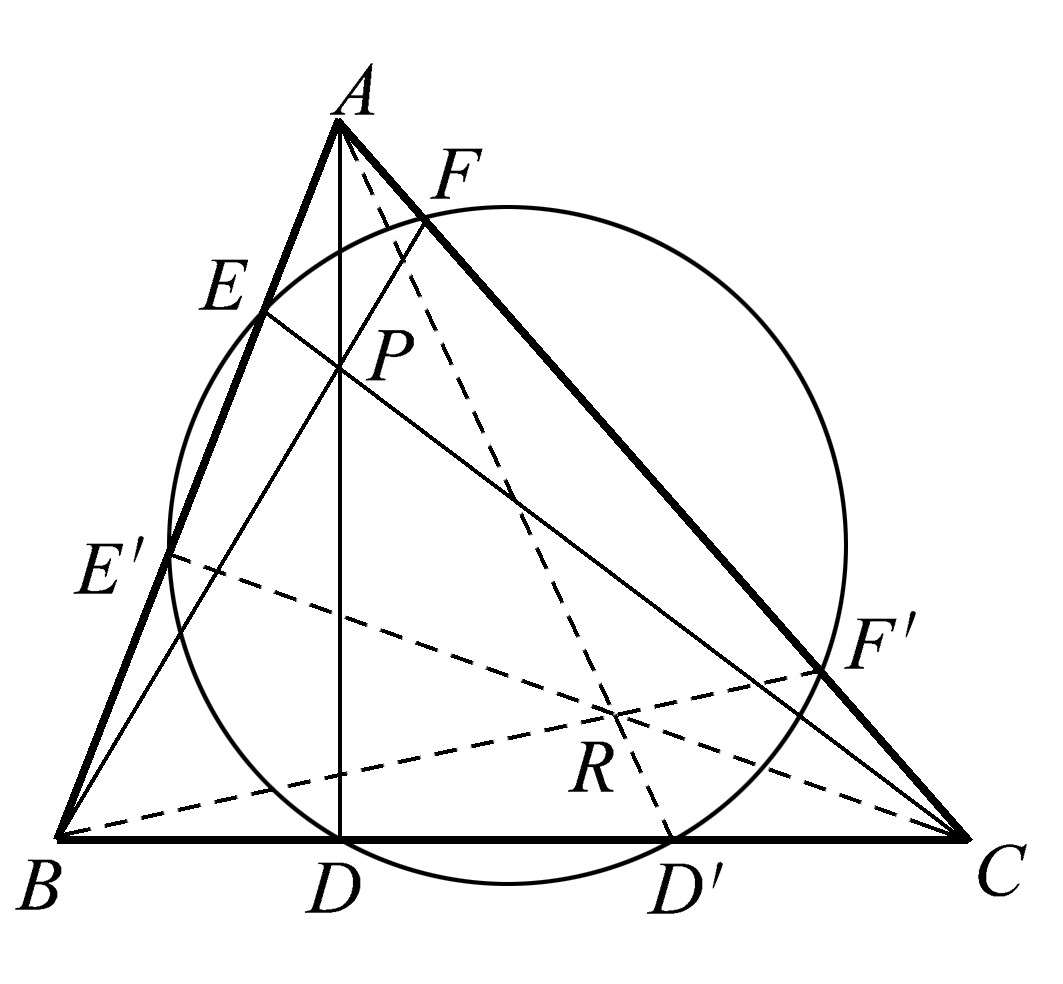
图1.44
类似地,我们现在在三角形 ABC 中选择一个点 P ,如图1.45所示,从点 P 向三角形的三边作垂线 PD 、 PE 、 PF 。我们知道任意三个非共线点确定一个唯一的圆,因此我们作出由点 D 、 E 、 F 确定的那个圆。
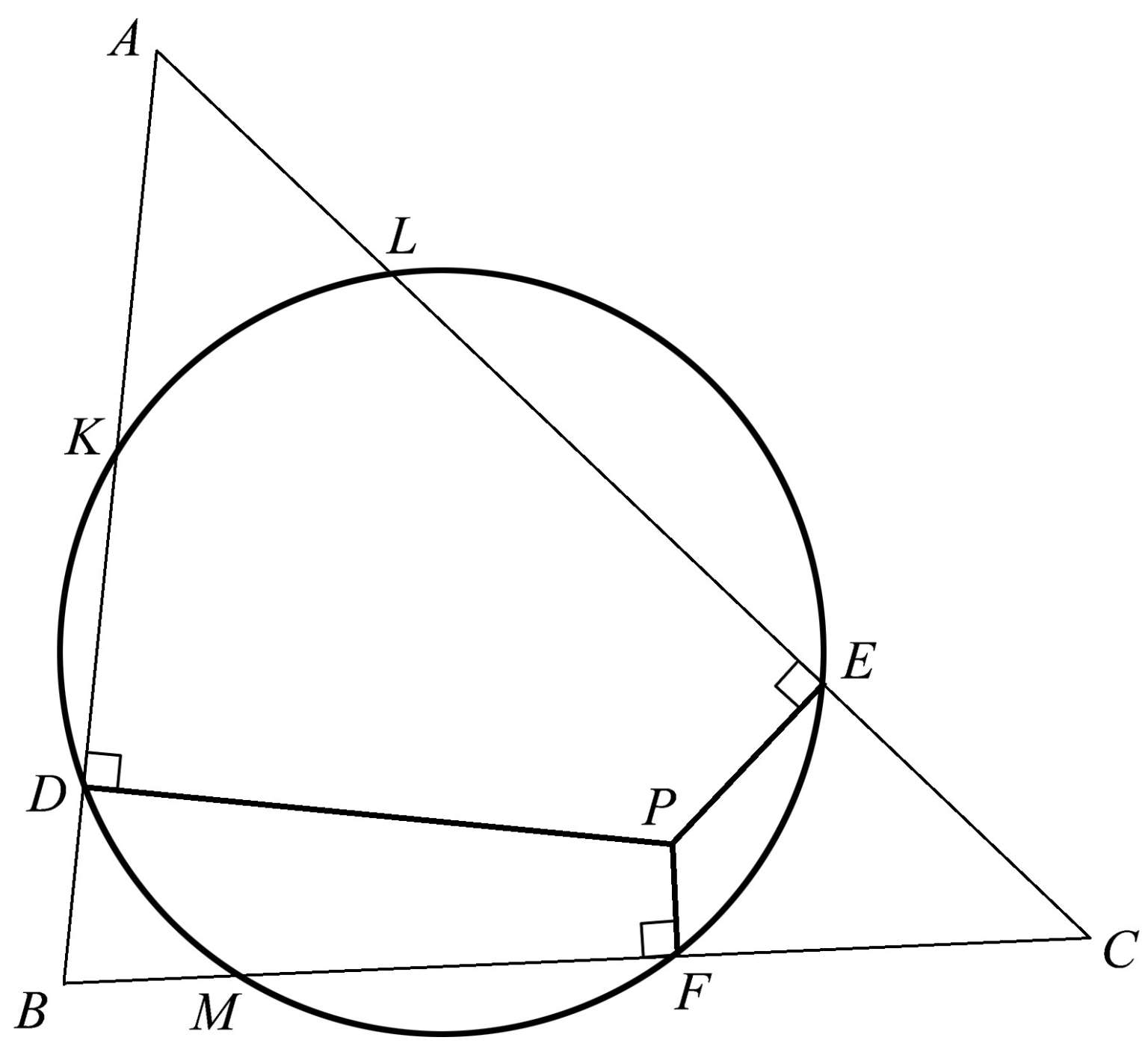
图1.45
请注意,该圆还与三角形相交于另外三个点 K 、 L 、 M ,如图1.46所示。然后我们在点 K 、 L 、 M 处作三角形 ABC 各边的垂线,你可以看出,这些垂线是共点的。请记住,我们是从一个随机选择的点 P 开始的,然后让三个垂足确定的那个圆又决定了另外三个似乎与前三个点无关的点。但是,你瞧,这三个新的点引出的三条垂线同样具有共点性。
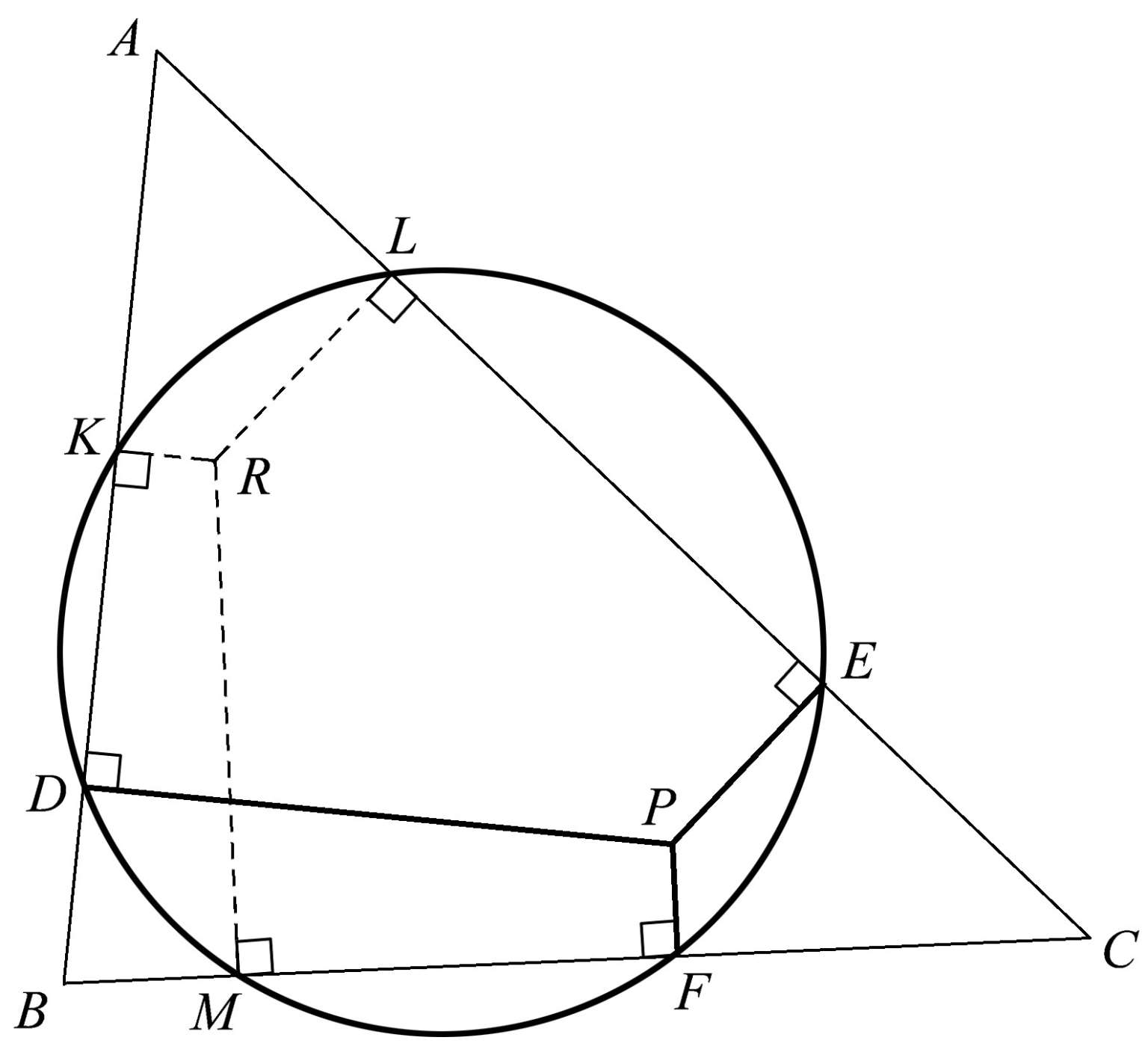
图1.46
我们已经讨论过一个既不内切也不外接于三角形的圆。现在我们来讨论其他情况,考虑一个外接于一个三角形的圆,以及一个内切于同一个三角形的圆。这将得到一些意想不到的共点性。在图1.47中,圆心为 O 的圆内切于三角形 ABC ,与各边的切点为 T 、 U 、 V 。圆心为 I 的圆外接于三角形 ABC ,其各边的垂直平分线(它们确定了外接圆的圆心)与该圆相交于点 K 、 L 、 J 。

图1.47
将最后确定的点 K 、 L 、 J 与内切圆上的切点( T 、 U 、 V )相连,就得到了三条共点线,如图1.48所示。
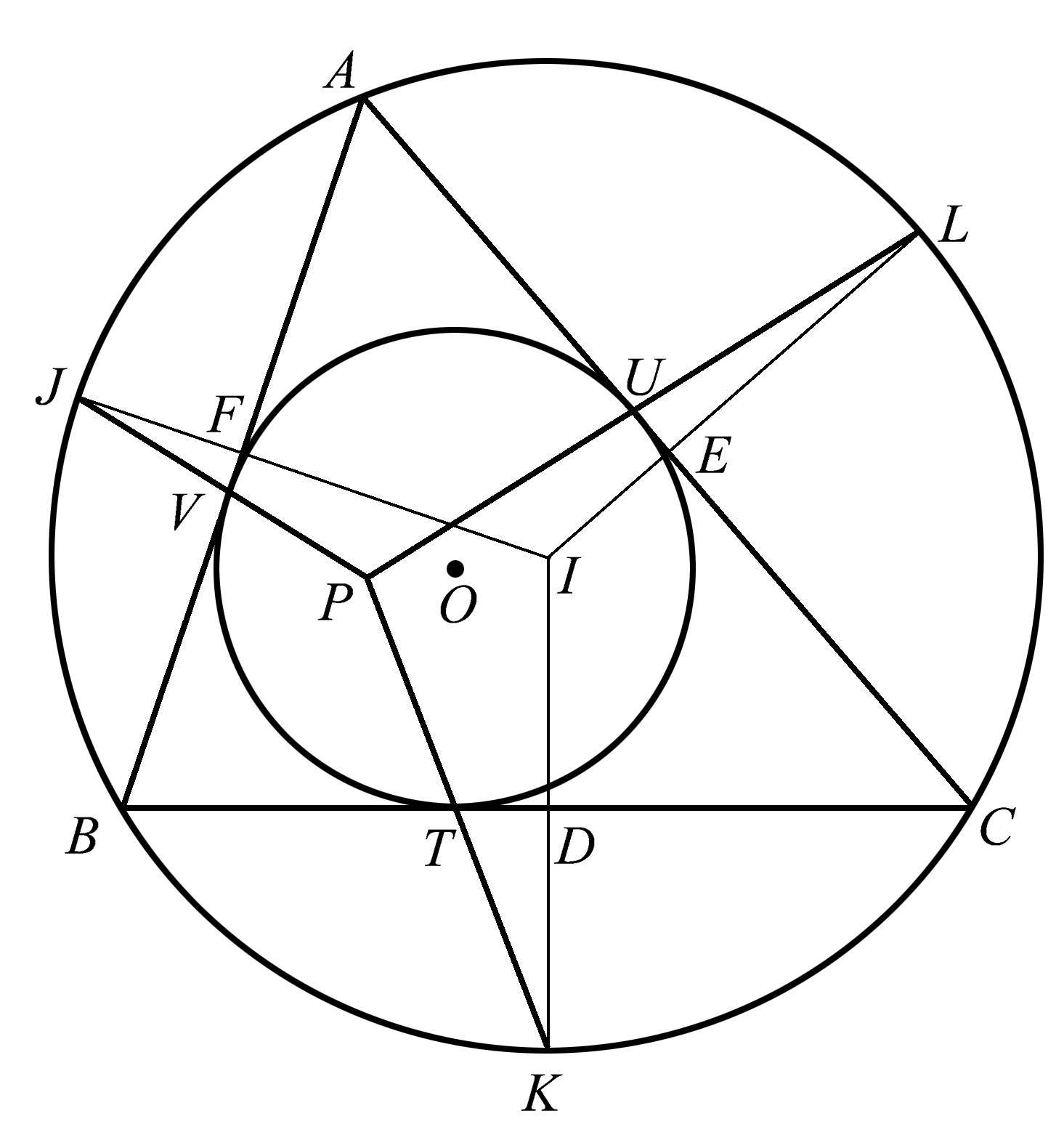
图1.48
你可能注意到,图1.49中的点 P 、 O 、 I 看起来是共线的,也就是说,这三个点都位于同一条直线上。事实上,我们可以证明确实如此。花点时间去欣赏这些共点性和共线性,虽然它们往往被忽视,却令人着迷。我们将在下一章讨论共线性。但由于点 P 、 O 、 I 显然在一条直线上,因此我们就提前提一下。
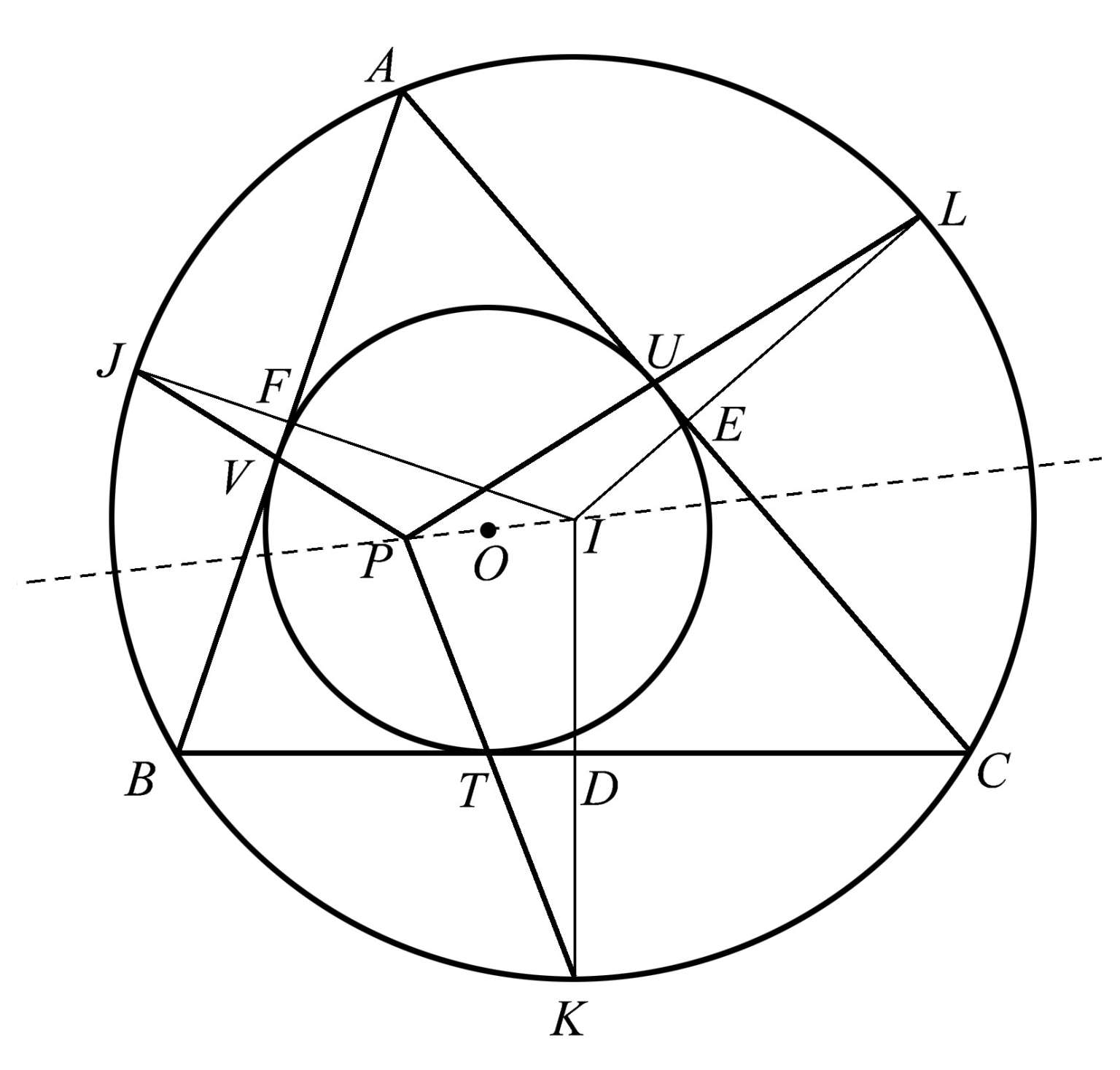
图1.49
我们现在将内切圆的概念延伸到三角形以外,考虑与三角形外接圆相切并与三角形一边相切的那些圆。图1.50显示了这样的一种构形。最简单的构造方法是作各边的垂直平分线(它们当然共点于外接圆的圆心),然后确定两个切点之间的中点。一旦你有了这些中点,你就有了这些圆的圆心以及它们各自的半径,从而可以作出这三个圆。
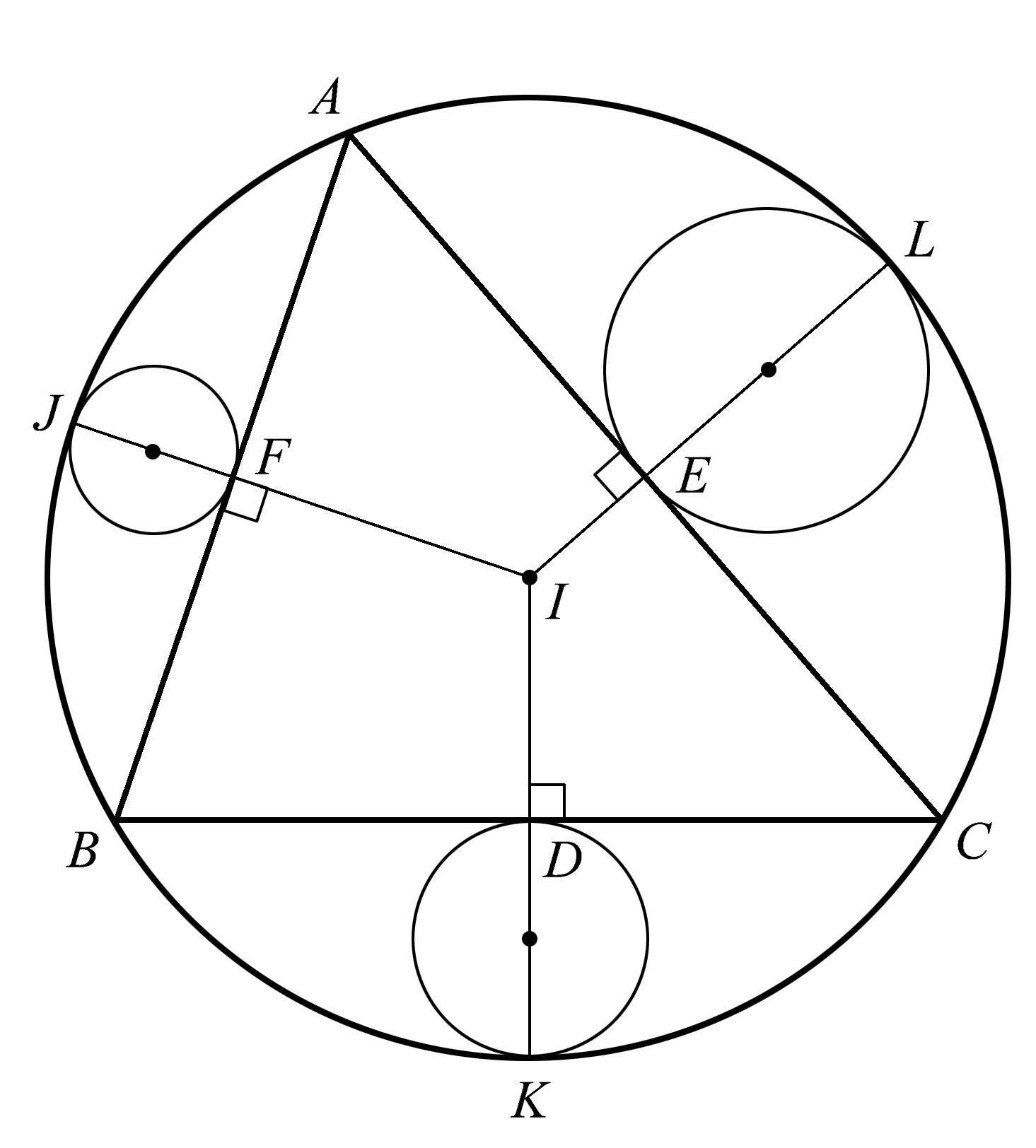
图1.50
通过将各对相切圆的切点与三角形的相对顶点连接起来,可以获得神奇的共点性。如图1.51所示,其中直线 AK 、 BL 、 CJ 共点于点 P 。请记住,我们是从一个任意画出的三角形开始的,这就是这个结果如此精彩的原因。
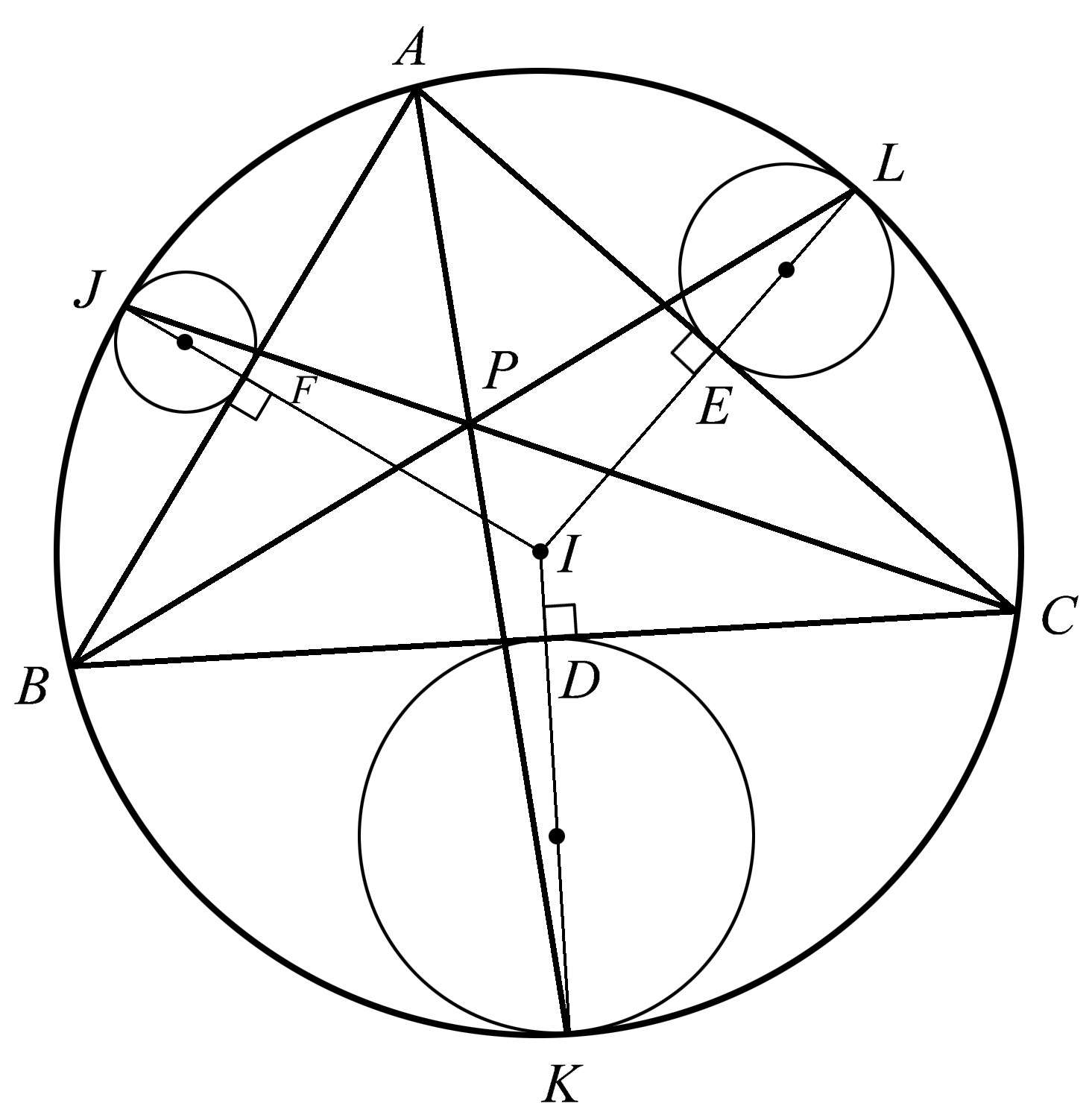
图1.51
在我们探讨下一个神奇的共点性之前,我们必须首先认识到,连接三角形三条边的中点(如图1.52所示),可以将三角形分成四个全等三角形。此外,如果你仔细看这个图,你还会发现其中有三个平行四边形: AEDF 、 DFEC 、 BFED 。
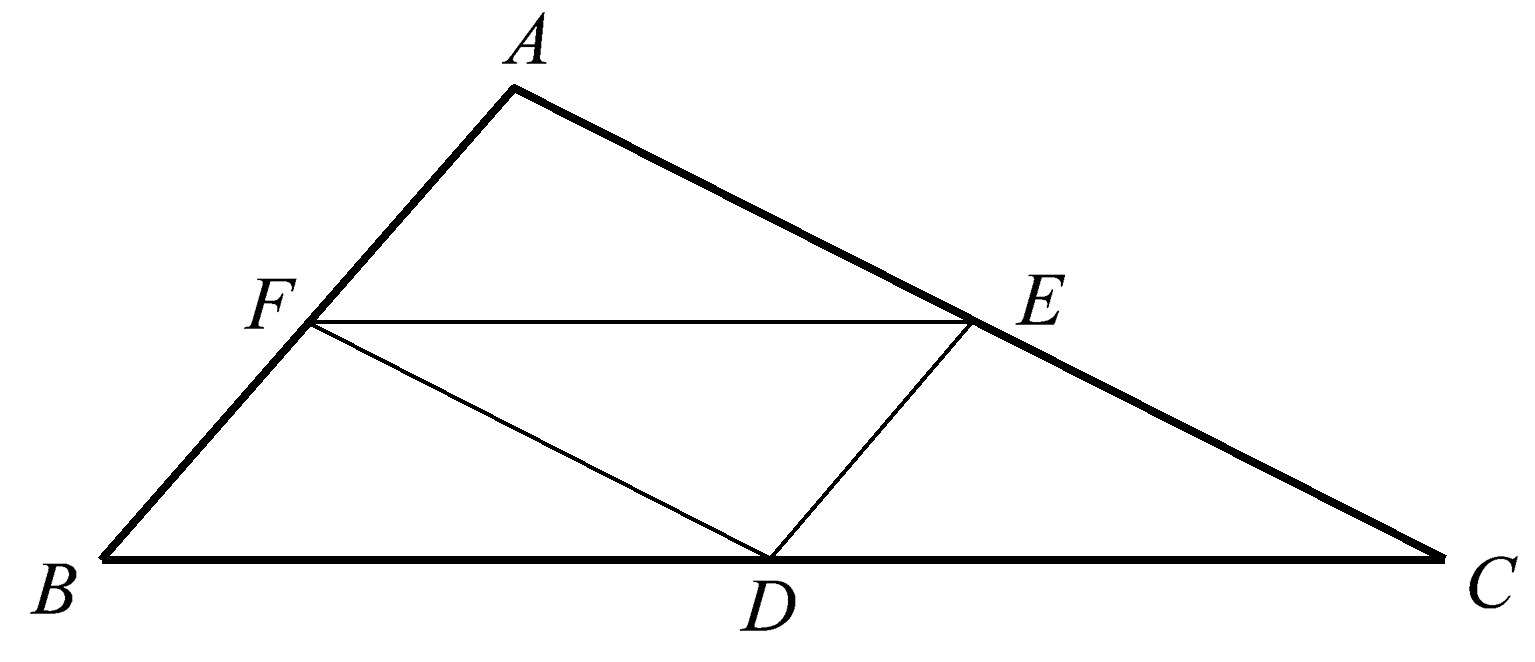
图1.52
如图1.53所示,在每个三角形中作一个内切圆,再将每个圆的圆心与中心的那个三角形的远端顶点连接起来,便可以确立另一个共点性,即 QD 、 ER 、 FS 相交于点 P ,这是另一个神奇的共点性的例子,它显示了几何之美。

图1.53
在这个构形中,将大三角形 ABC 各顶点与其近邻的小圆圆心相连,也能确定一个共点性,如图1.54所示。可以看到,图中 AQ 、 BR 、 CS 相交于点 P 。

图1.54
我们可以再进一步,考虑 AQ 、 BR 、 CS 与三角形 DEF 的最近边的交点 J 、 L 、 K ,如图1.55所示。令人惊讶的是,连接三角形 DEF 各顶点与点 J 、 K 、 L 的三条直线相交于点 P 。我们再次在这个构形中发现了共点性。志存高远的读者可以在其中寻找更多的共点性。
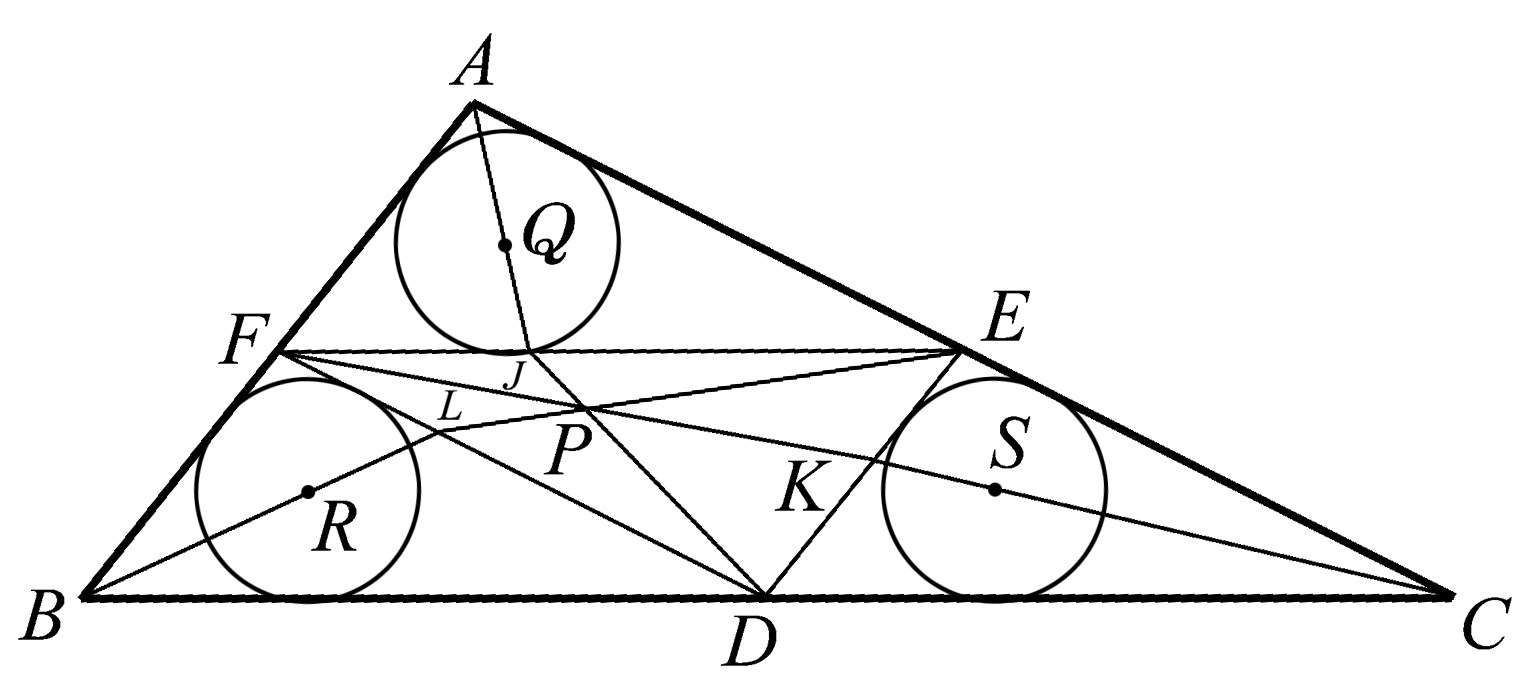
图1.55
接下来,我们研究的范围既包括一个三角形的内部,也包括它的外部。圆心为 P 、 Q 、 O 的三个圆分别与三角形 ABC 的一边及其他两边的延长线相切。这样的圆称为旁切圆,而在三角形内与各边相切的圆称为内切圆。图1.56清楚地标明了这些圆与三边的切点。圆心为 P 的圆与三角形的三边相切于点 H 、 F 、 G 。圆心为 Q 的圆与三角形的三条边相切于点 R 、 E 、 N 。圆心为 O 的圆与三角形的三条边相切于点 J 、 D 、 M 。这一构形产生了许多共点线:
AD 、 BE 、 CF 共点于点 X 。
PC 、 AO 、 QB 共点于点 Y 。
此外还有许多共线点,例如 P 、 A 、 Q ; P 、 B 、 O ; Q 、 C 、 O 。
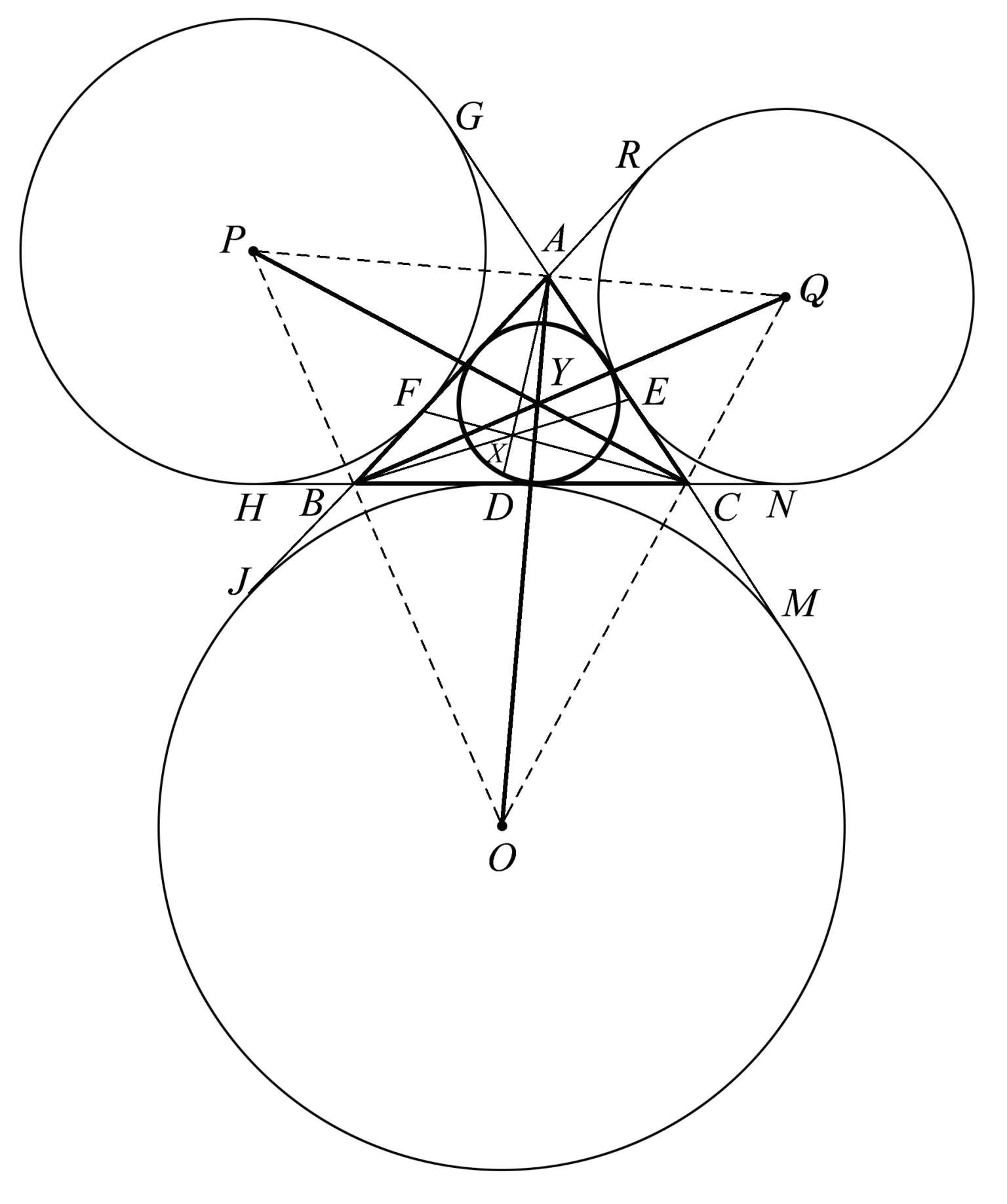
图1.56
感兴趣的读者还可以在这个神奇的图中找出其他共线性或共点性。
接下来,我们考虑三个不同大小的圆,除了同时与两个圆相切的那些切线之外,它们之间没有其他联系,如图1.57所示。将这些公切线的三个交点 R 、 T 、 S 与其相对的圆心连接起来,我们再次发现了一个惊人的共点性。请注意,这些圆是随机放置的。这就使得这种共点性更加惊人!
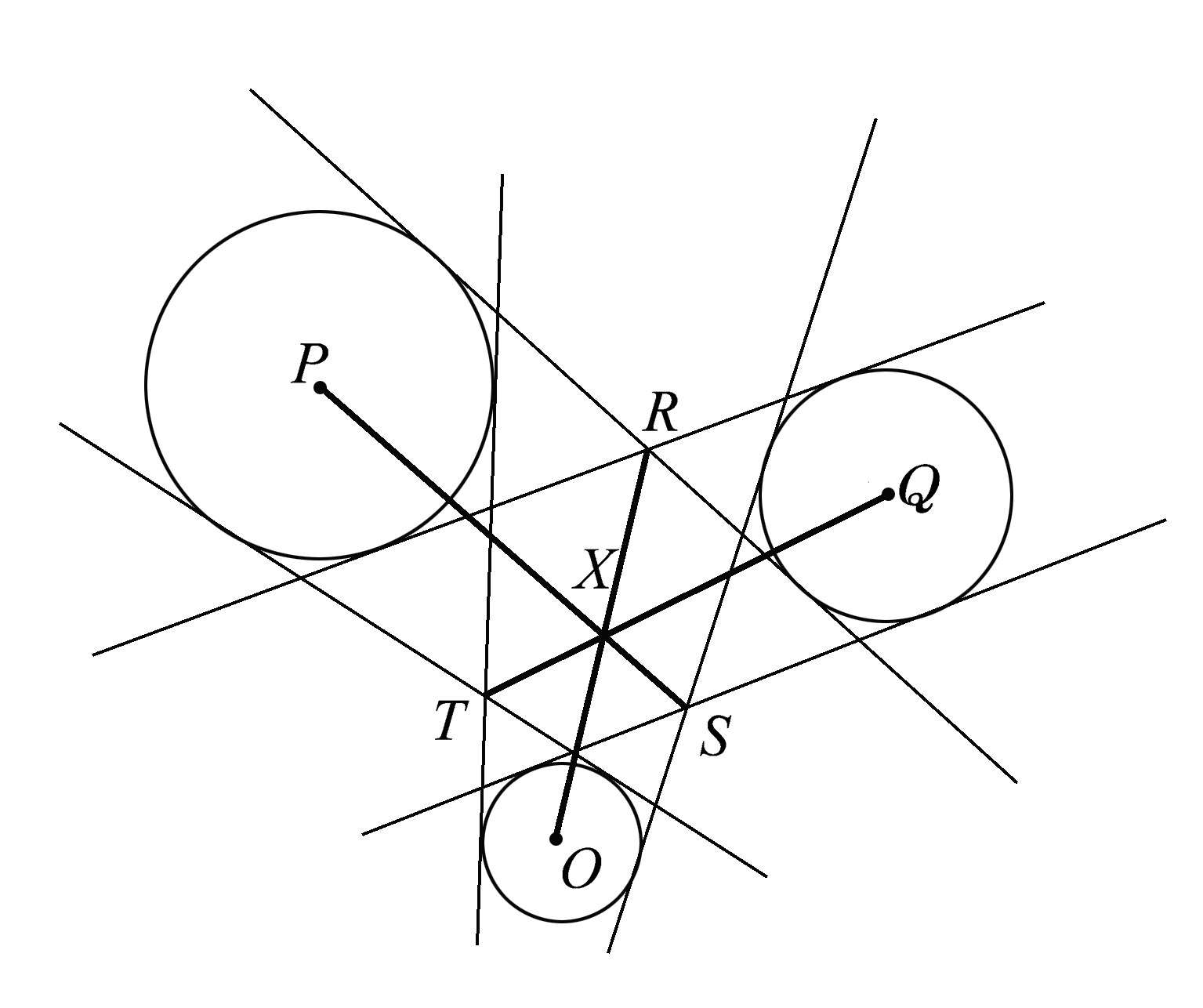
图1.57
一个著名的关系——以任意三角形的三条边为底边向外构造三个等边三角形。拿破仑·波拿巴(Napoleon Bonaparte,1769—1821)也是一位数学爱好者,人们认为是他发现了这一关系。如图1.58所示,从原始三角形的每个顶点到其对边上的等边三角形的远端顶点的连线是共点的。请注意,三角形 ABC 可以是任何形状,这种关系永远成立。此外,这三条共点线段的长度相等: AE = BD = CF 。

图1.58
此外,当连接这三个等边三角形的中心 P 、 Q 、 R 时,就形成了另一个等边三角形,如图1.59所示。这一构形通常被称为拿破仑三角形。

图1.59
这个拿破仑三角形还有一些其他性质。三个等边三角形的外接圆共点于点 O ,而点 O 就是最初的三条直线 AE 、 BD 、 CF 的公共点,如图1.60所示。
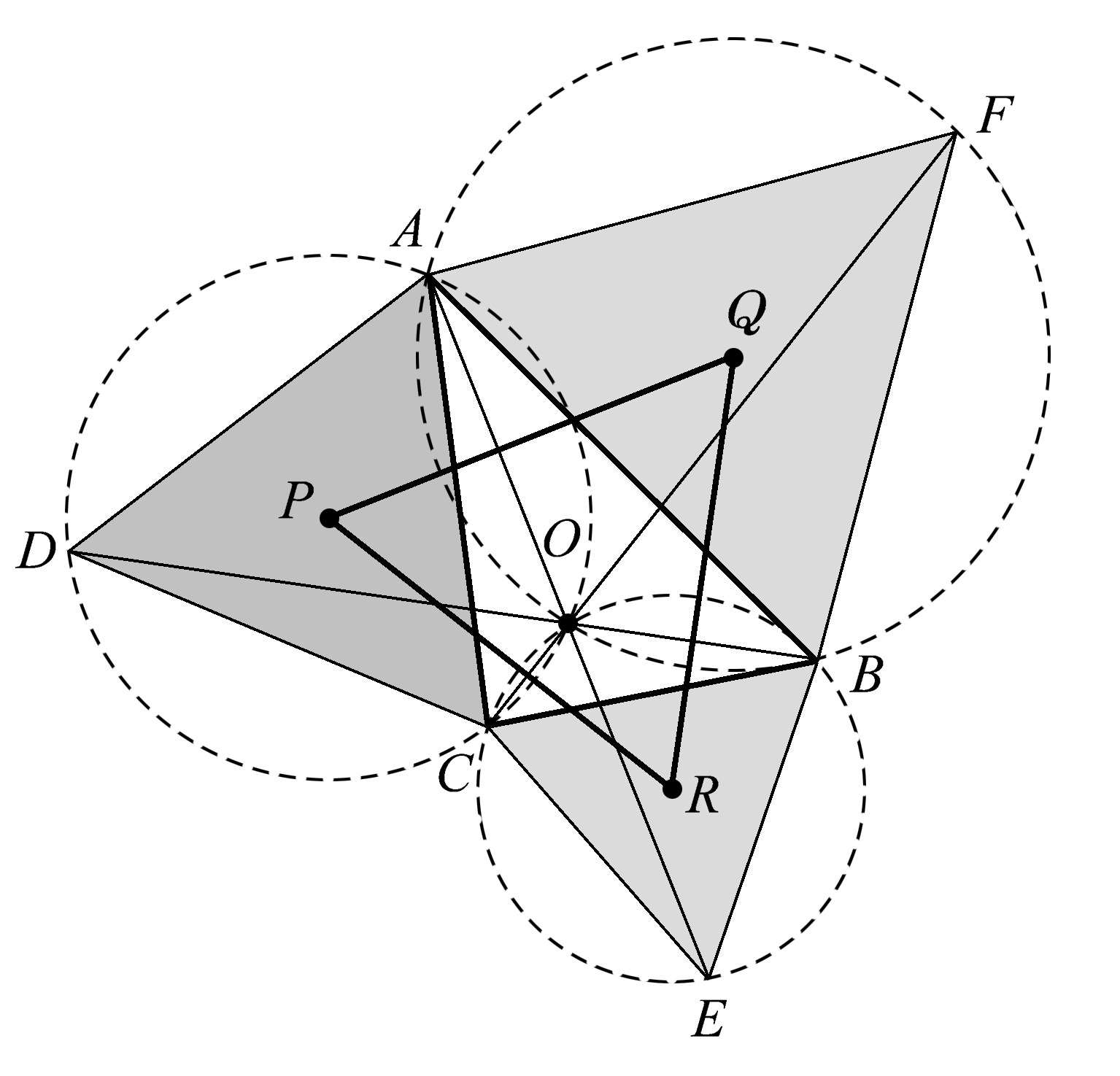
图1.60
我们继续在这个神奇的几何构形中探索更多的美。点 O 被称为三角形 ABC 的等角点,因为∠ AOB = ∠ BOC = ∠ COA ,如图1.61所示。
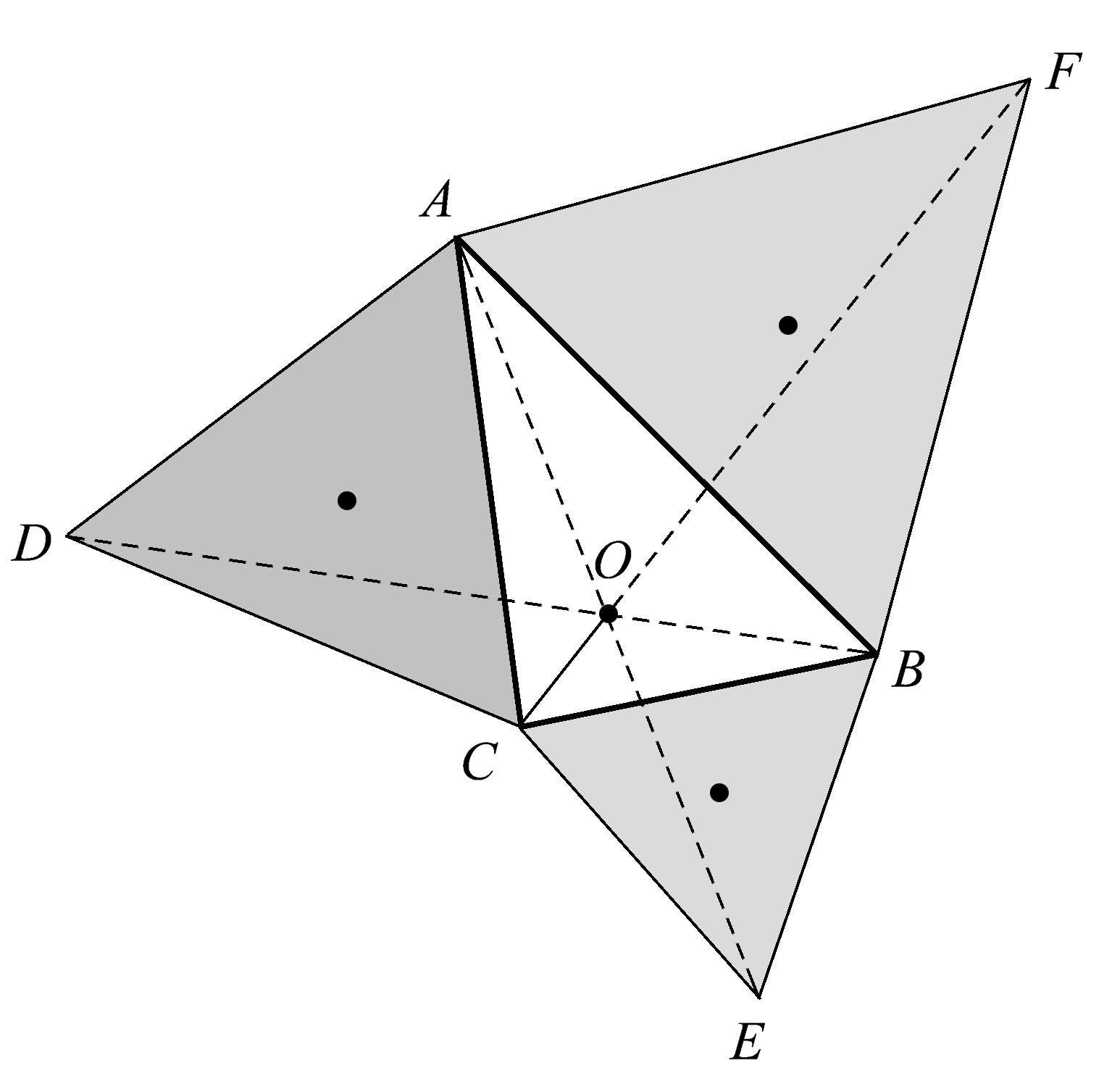
图1.61
在拿破仑三角形中,还有一个令人惊讶的等边三角形。我们以线段 AD 和 DC 为边,作一个平行四边形,这样就得到了平行四边形 ADCK 。瞧!我们得到的三角形 AKF 又是一个等边三角形,如图1.62所示。

图1.62
我们已经讨论过在一个三角形的每条边上作等边三角形和圆的情形。接下来我们用一种不同寻常的方式构造一个三角形,它可以贴合一个给定三角形的任意一条边。我们将采用一种称为镜射的方法来实现,如图1.63所示,我们作三角形 ABC 关于直线 AC 的镜像,得到三角形 ADC 。可以从 B 点作垂直于 AC 的直线,垂足为点 G ,然后在 BG 的延长线上取点 D ,使得 GD = BG 。三角形 ADC 便是三角形 ABC 关于直线 AC 的镜像。
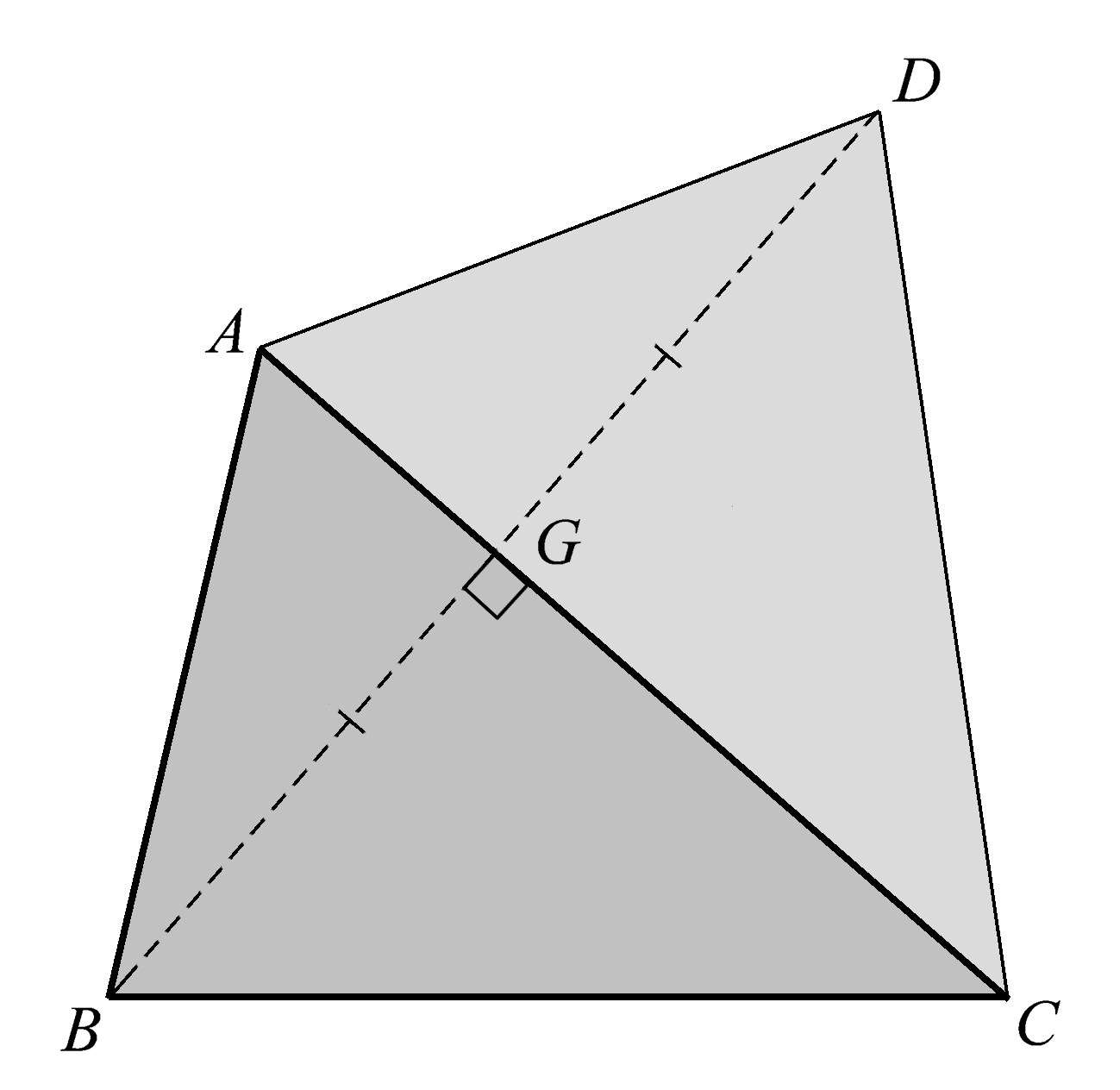
图1.63
我们接下来再进行两次类似的操作:将三角形 ABC 关于 AB 边镜射,得到三角形 ABE ;将三角形 ABC 关于 BC 边镜射,得到三角形 FBC ,如图1.64所示。
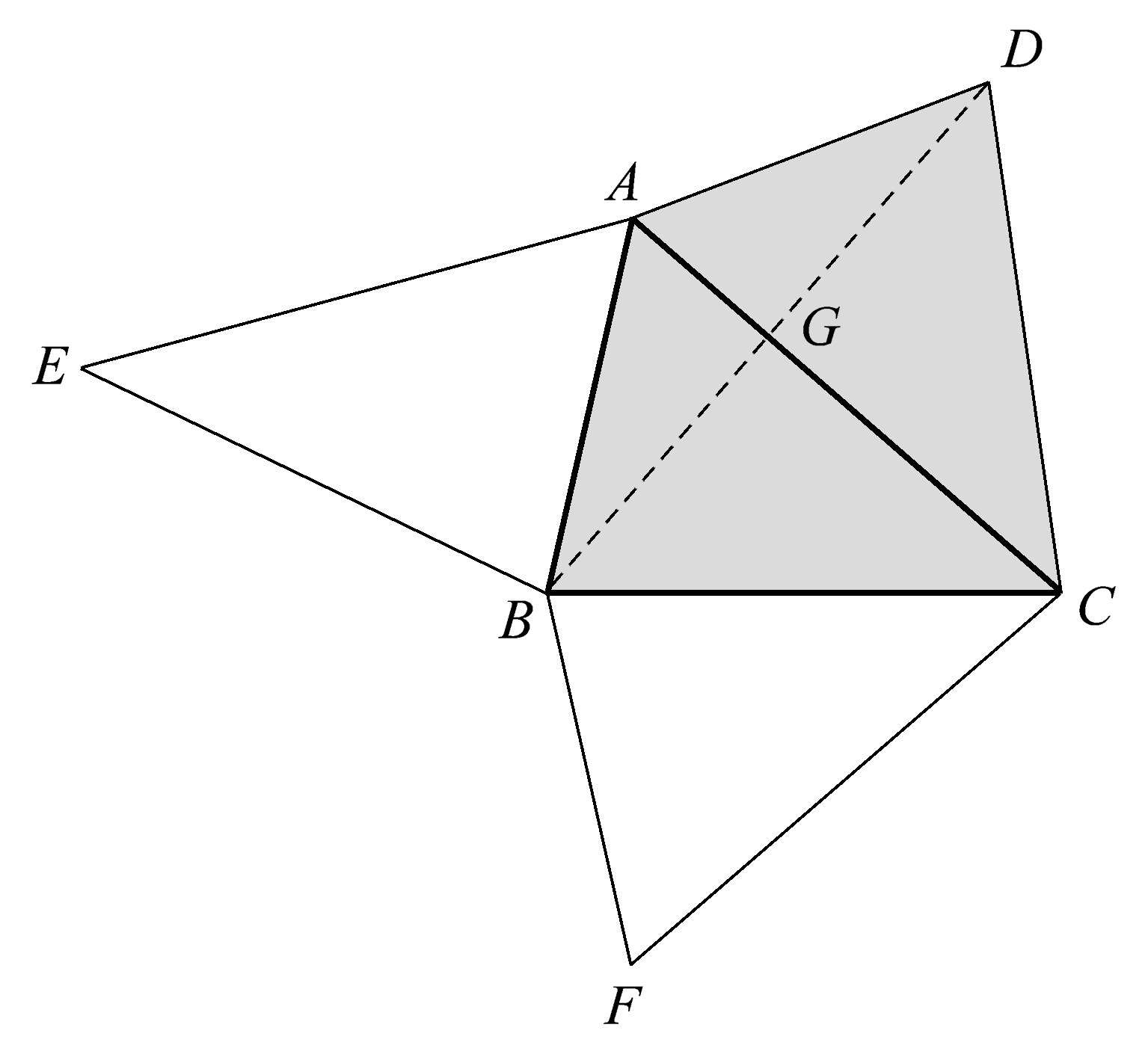
图1.64
现在我们有了三个新的三角形,每个三角形都与原来的三角形 ABC 全等,我们再作它们各自的外接圆,如图1.65所示。出乎意料的是,这三个圆是共点的。换句话说,它们有一个公共交点 P 。
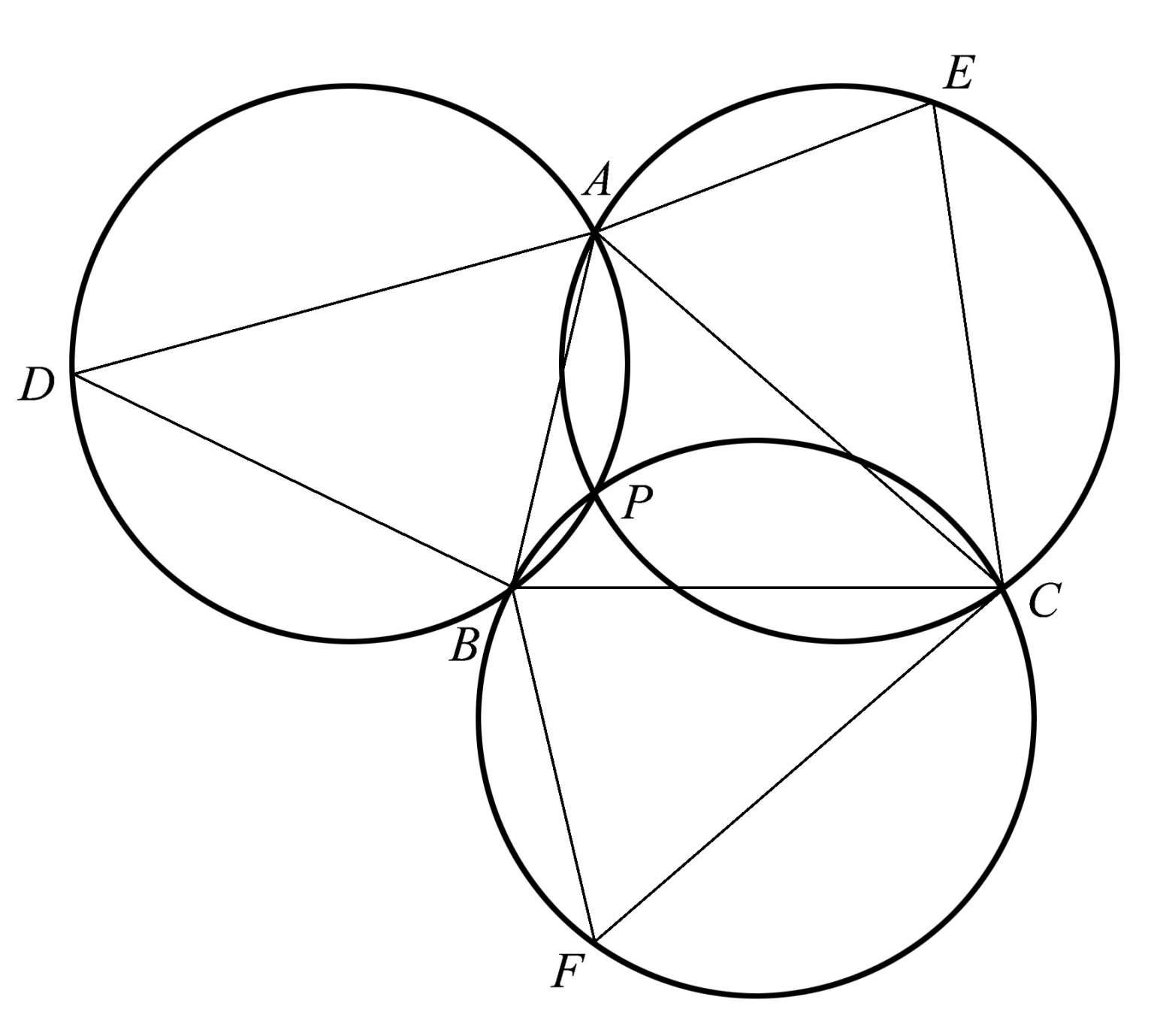
图1.65
如果你意犹未尽,我们还可以找到另一个公共点,这一次又是共点线。如图1.66所示,将每个圆的圆心与原始三角形 ABC 的远端顶点连接起来,三条共点线就出现了。我们观察到,直线 AS 、 BQ 、 CR 共点于点 O 。
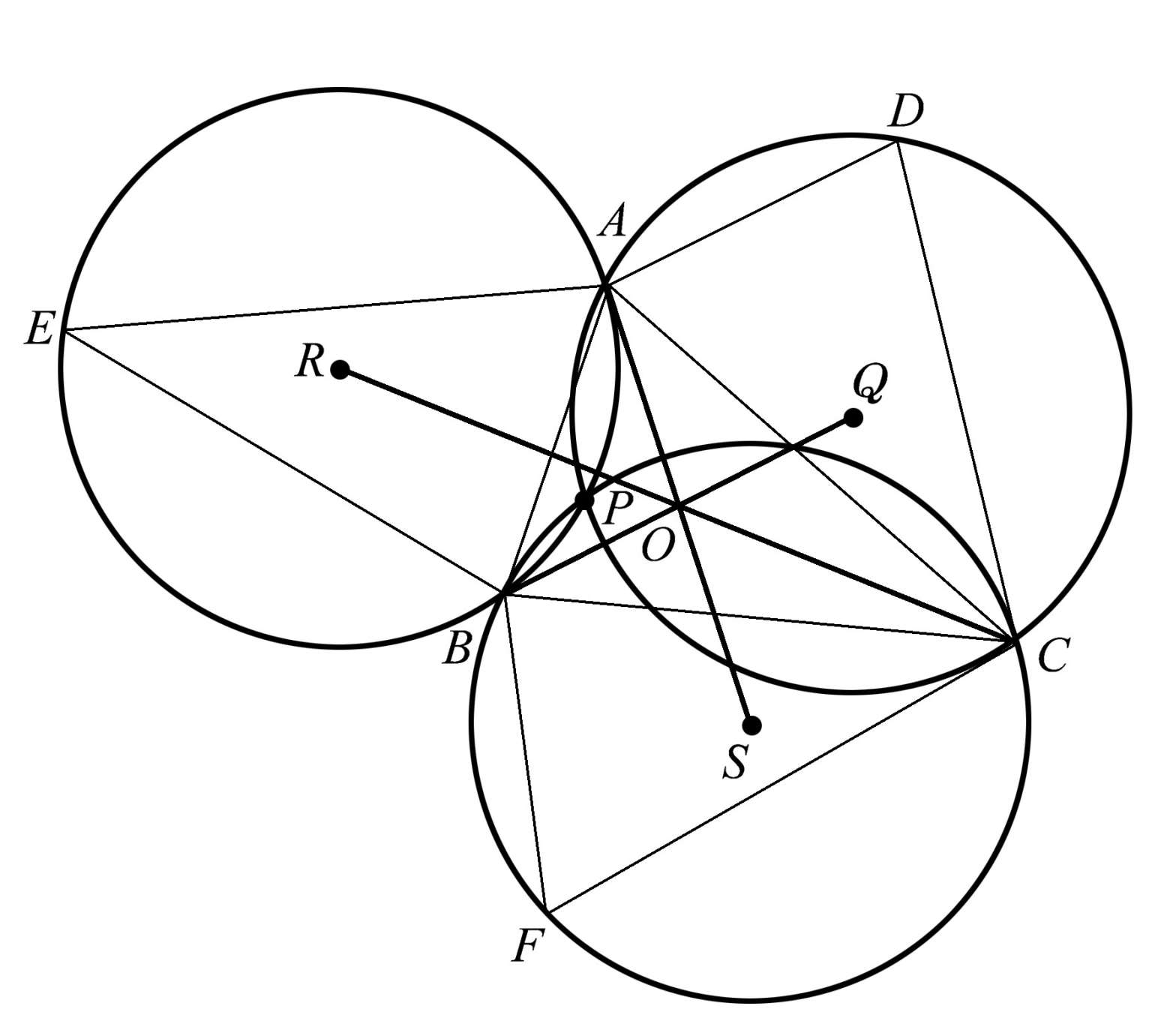
图1.66
让我们回到拿破仑三角形上来,且运用我们新掌握的技巧——用一个三角形的一条边镜射出另一个三角形。如图1.67所示,将等边三角形关于各条边作镜像。请注意,将这些镜射出的三角形(虚线)的中心点相连,就又得到一个等边三角形 P′R′Q′ 。
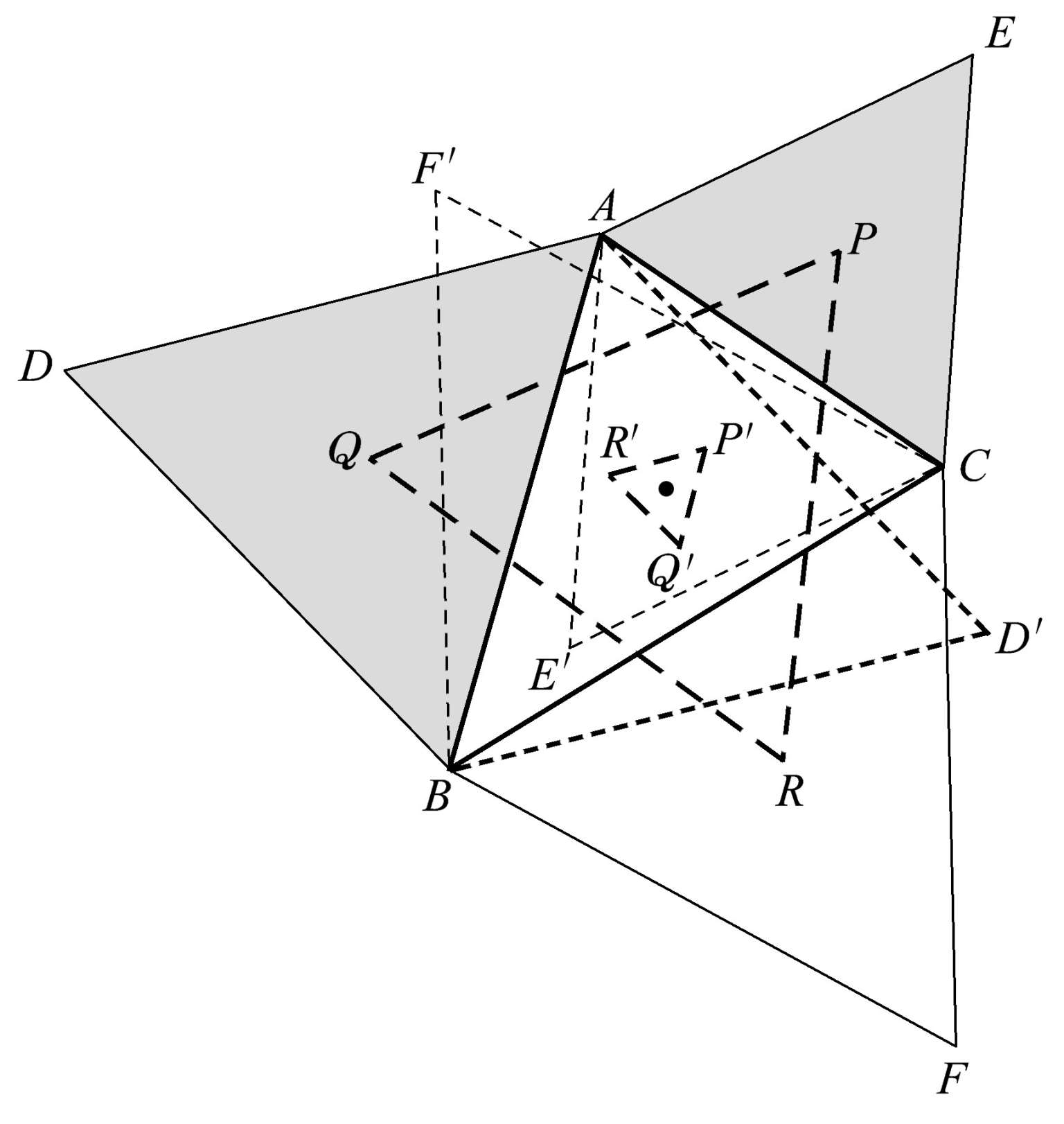
图1.67
连接三角形各边的中点,将其分为四个全等三角形(我们在图1.52中已经遇到过),就可以得到一组有趣的共点圆。三个“外围”三角形的外接圆相交于点 P ,如图1.68所示。
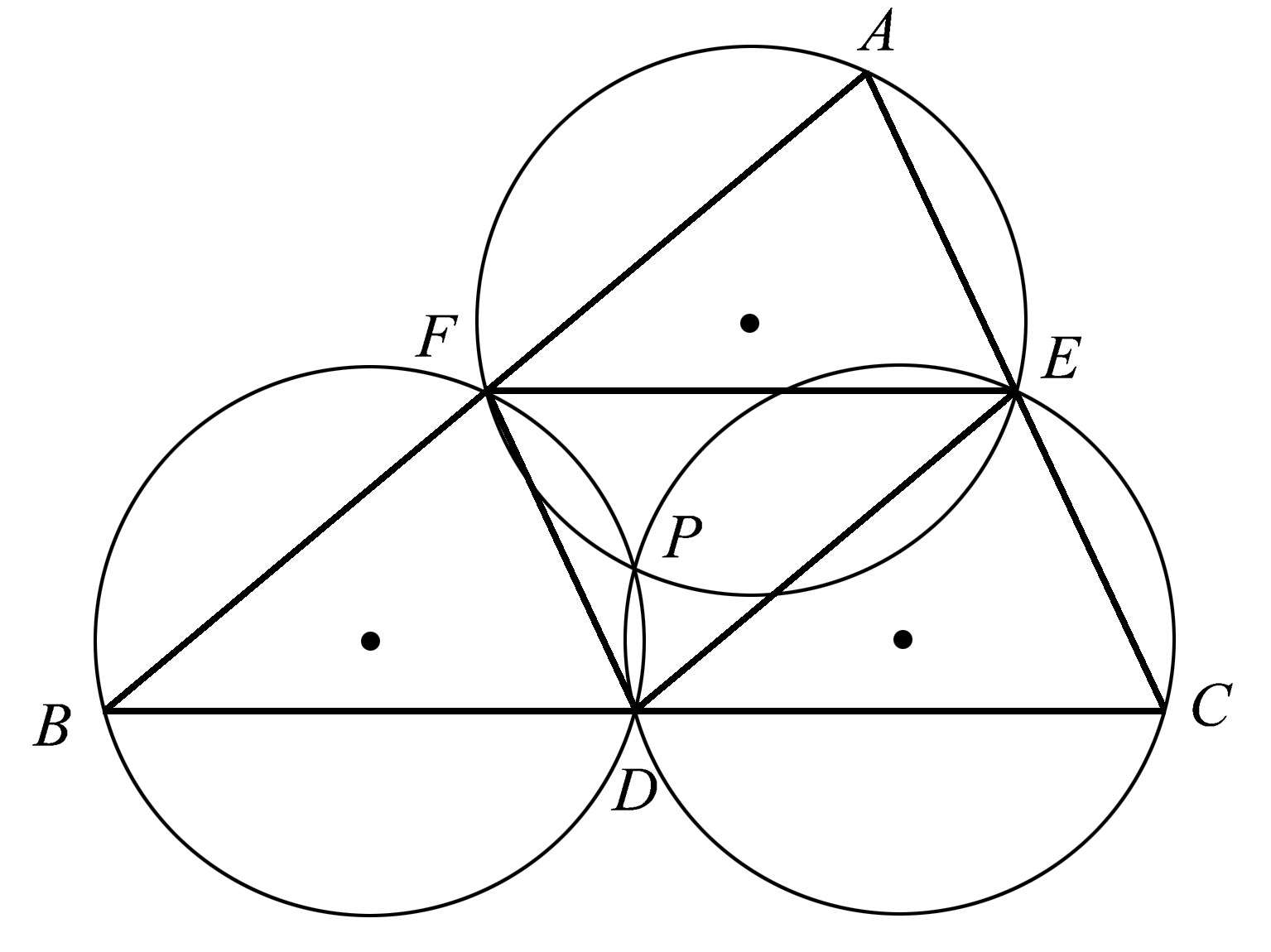
图1.68
这三个共点圆的另一个奇妙之处在于,把大三角形的各个顶点与其外接圆的圆心相连时,这三条线也是共点的。令人惊奇的是,这三条线的公共点与三个圆的公共点是同一点 P 。如图1.69所示。
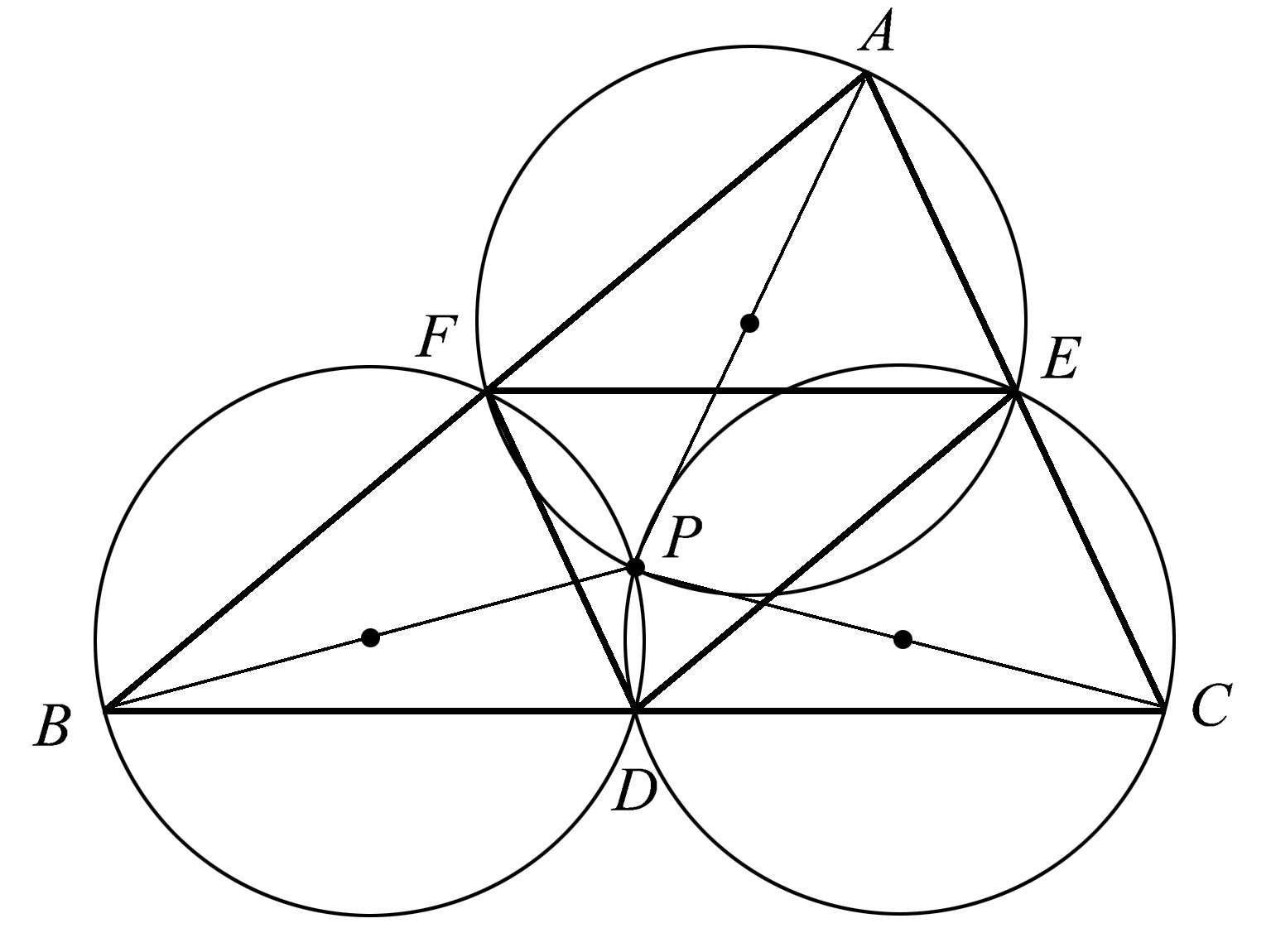
图1.69
将图1.69进一步推广,在三角形 ABC 的每一边上任取一点,由其中两点与三角形的一个顶点可确定一个圆,依此方法作出三个圆,如图1.70所示。请注意,这三个圆相交于一个公共点 P 。这一点被称为三角形的密克尔点,是以法国数学家密克尔(Auguste Miquel,1816—1851)的名字命名的,他首先发现了这一奇妙的关系。
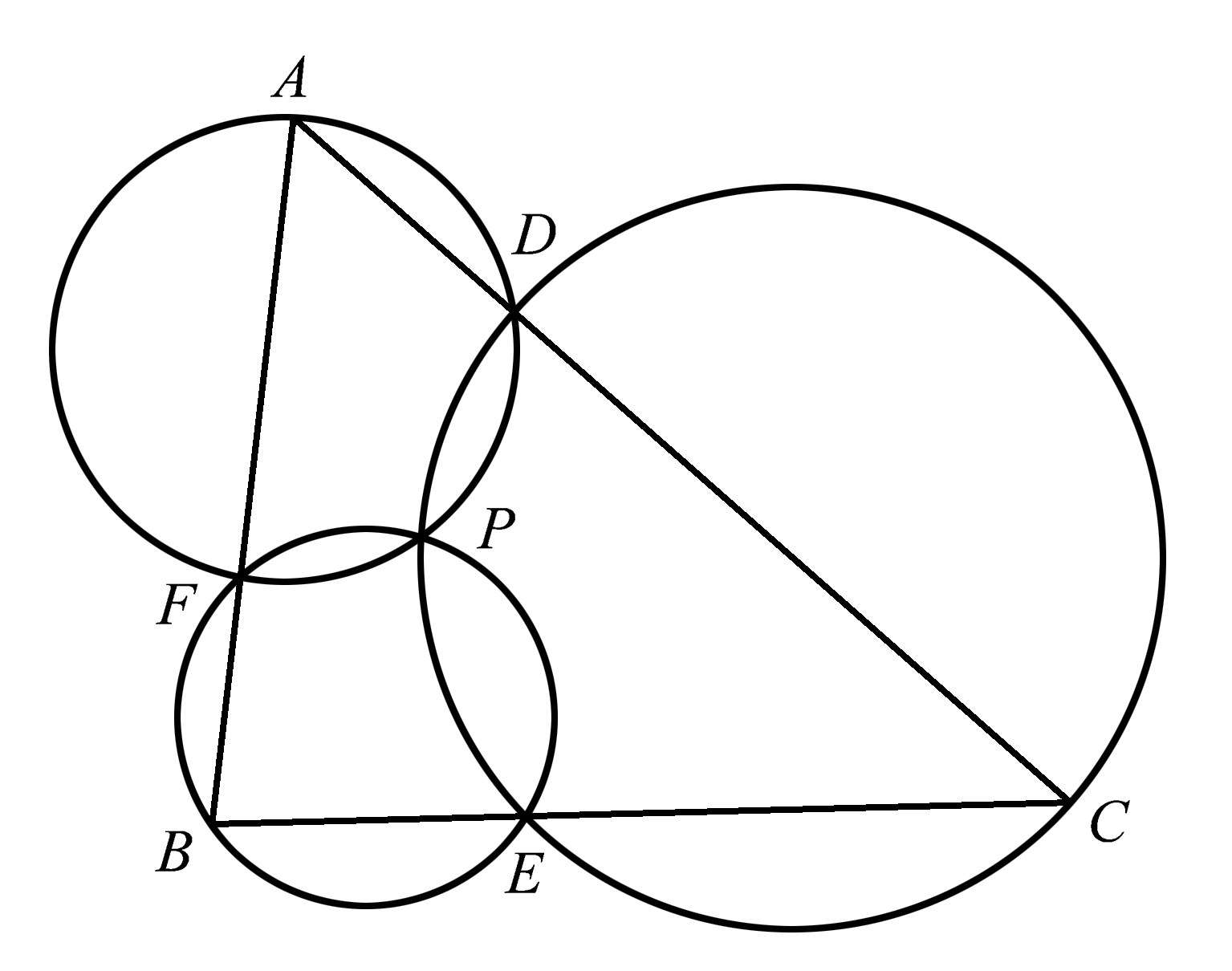
图1.70
关于密克尔点,还有一些有趣的特性。例如,把密克尔点与这些圆上的其他交点(在原始三角形的各边上)连接起来,这些线段与各边的夹角相等,即∠ AFP = ∠ CDP= ∠ BEP ,如图1.71所示。回想一下,我们是从任意三角形开始的,因此这个例子具有通用性,这种关系特别值得关注。
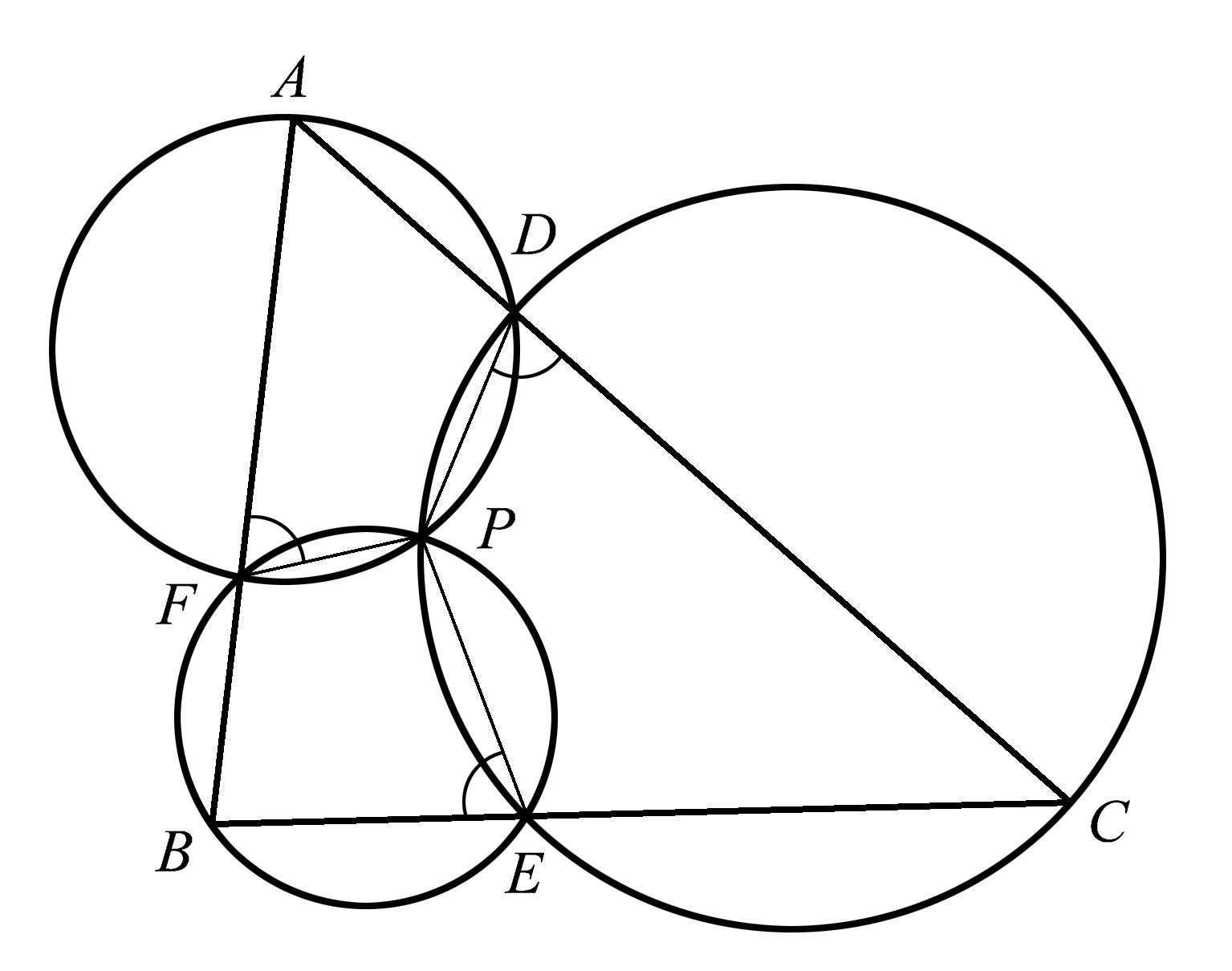
图1.71
请注意,对于某些三角形,例如钝角三角形,这三个圆的公共点 P 可能在三角形之外,如图1.72所示。那些锐角三角形的性质对于钝角三角形也成立。
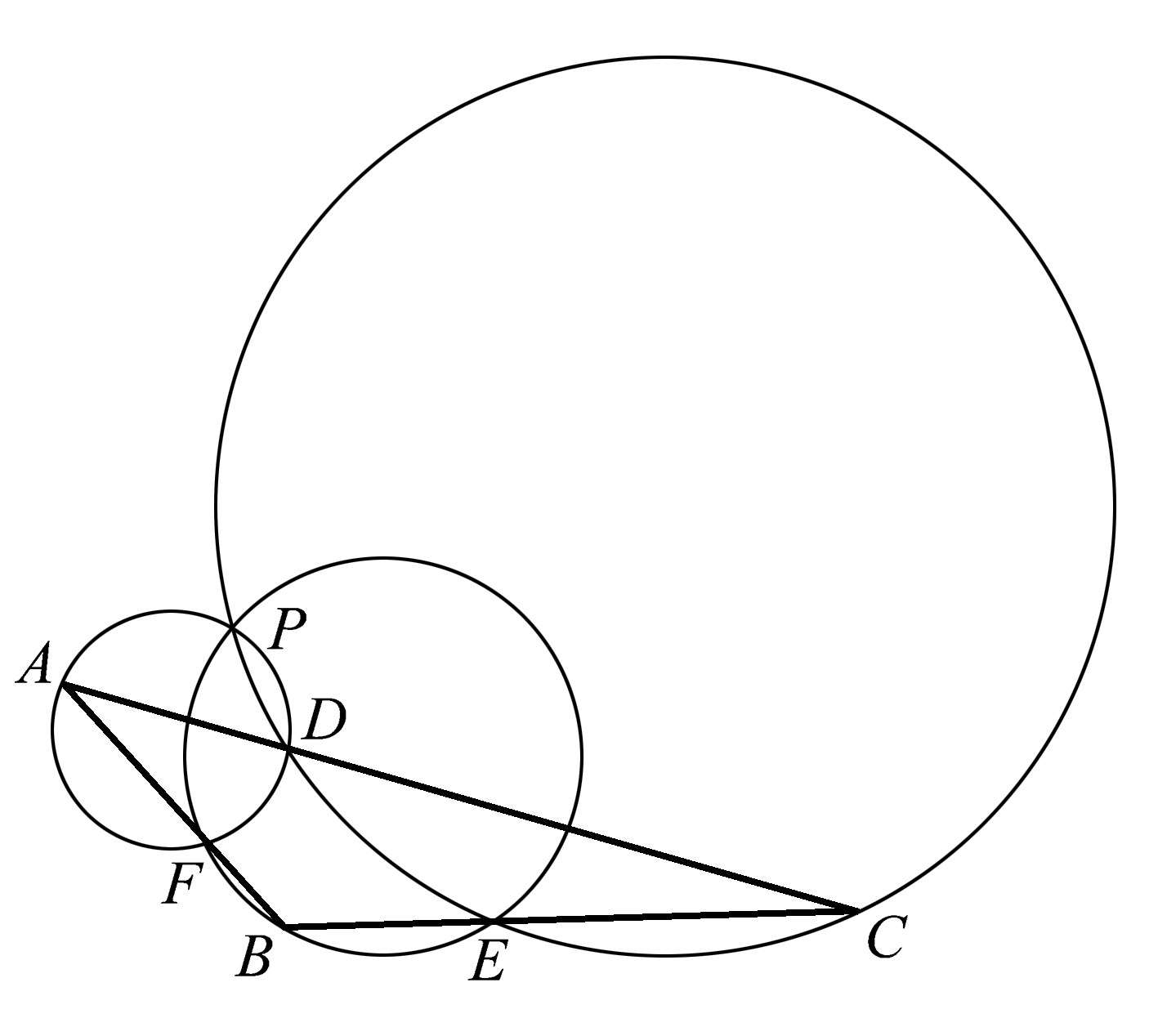
图1.72
此外,如果把密克尔构形中三个圆的圆心连接起来,就会惊奇地发现此时得到了一个与原来的三角形相似的三角形。也就是说,在图1.73中,三角形 ABC 与三角形 RSQ 相似,因为它们的三个对应角是相等的,这在图中已标明。当然,这也适用于钝角三角形。

图1.73
我们可以将这个密克尔构形再推进一步。考虑另一个任意三角形,它的每个顶点都在一个密克尔圆上,并且每条边都通过圆上的三个交点之一。这个三角形相似于原始三角形。如图1.74所示,作三角形 ABC 的一个密克尔构形,然后作三角形 GHK ,使其三个顶点分别在三个圆上,三条边分别过交点 E 、 D 、 F 。这样我们就得到了一个与三角形 ABC 相似的三角形 GKH 。
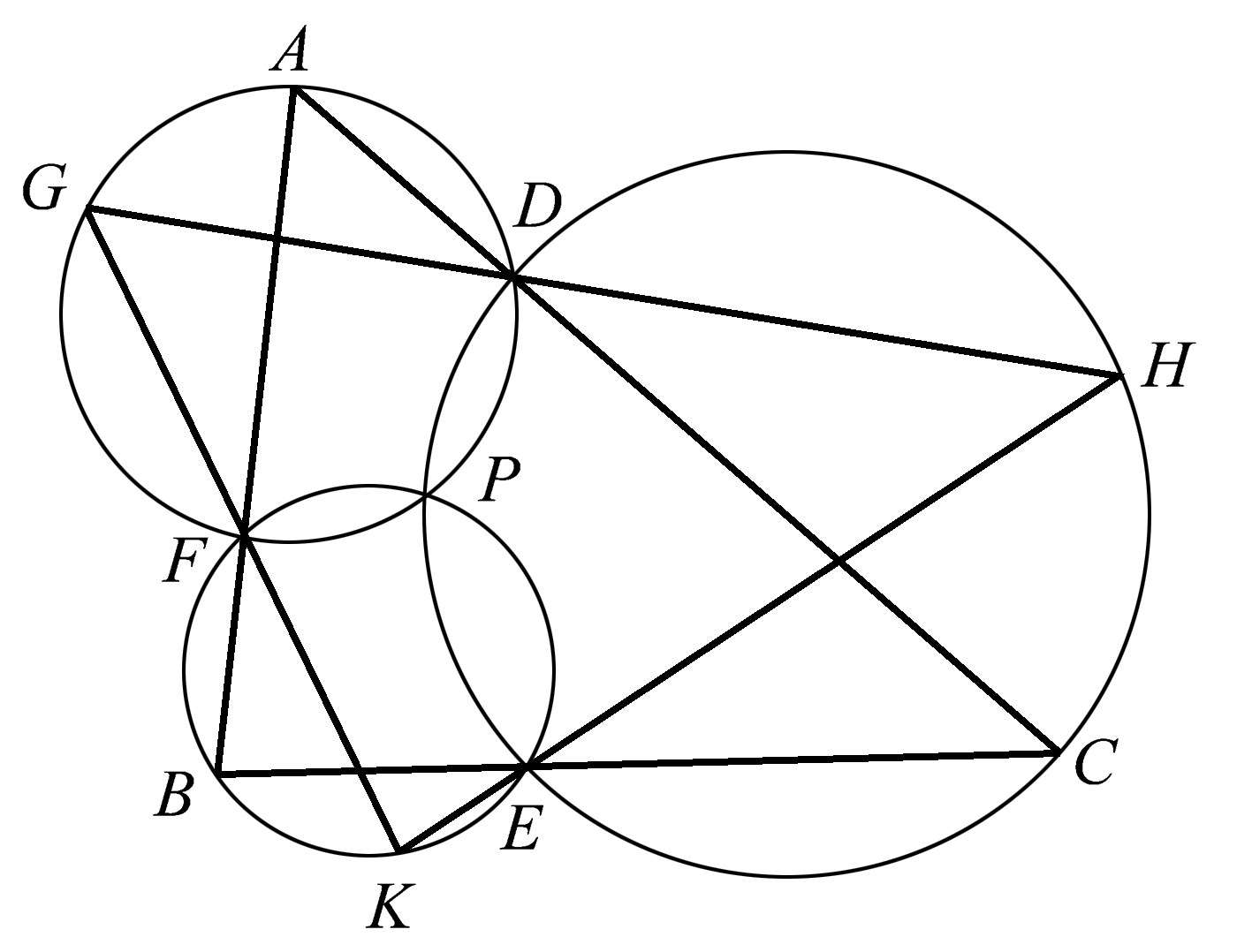
图1.74
值得注意的是,如果将三角形各边上的三点 E 、 D 、 F 中的两点移到三角形两边的延长线上,密克尔定理同样成立。如图1.75所示,此时点 F 和 E 不在三角形 ABC 的边上,而是在其延长线上。我们按照作密克尔圆的方法作三个圆,请注意,它们也共点于点 P 。当然,上述所有性质都将成立。此刻,你可能想知道密克尔定理是否还有更多应用。请继续往下看!
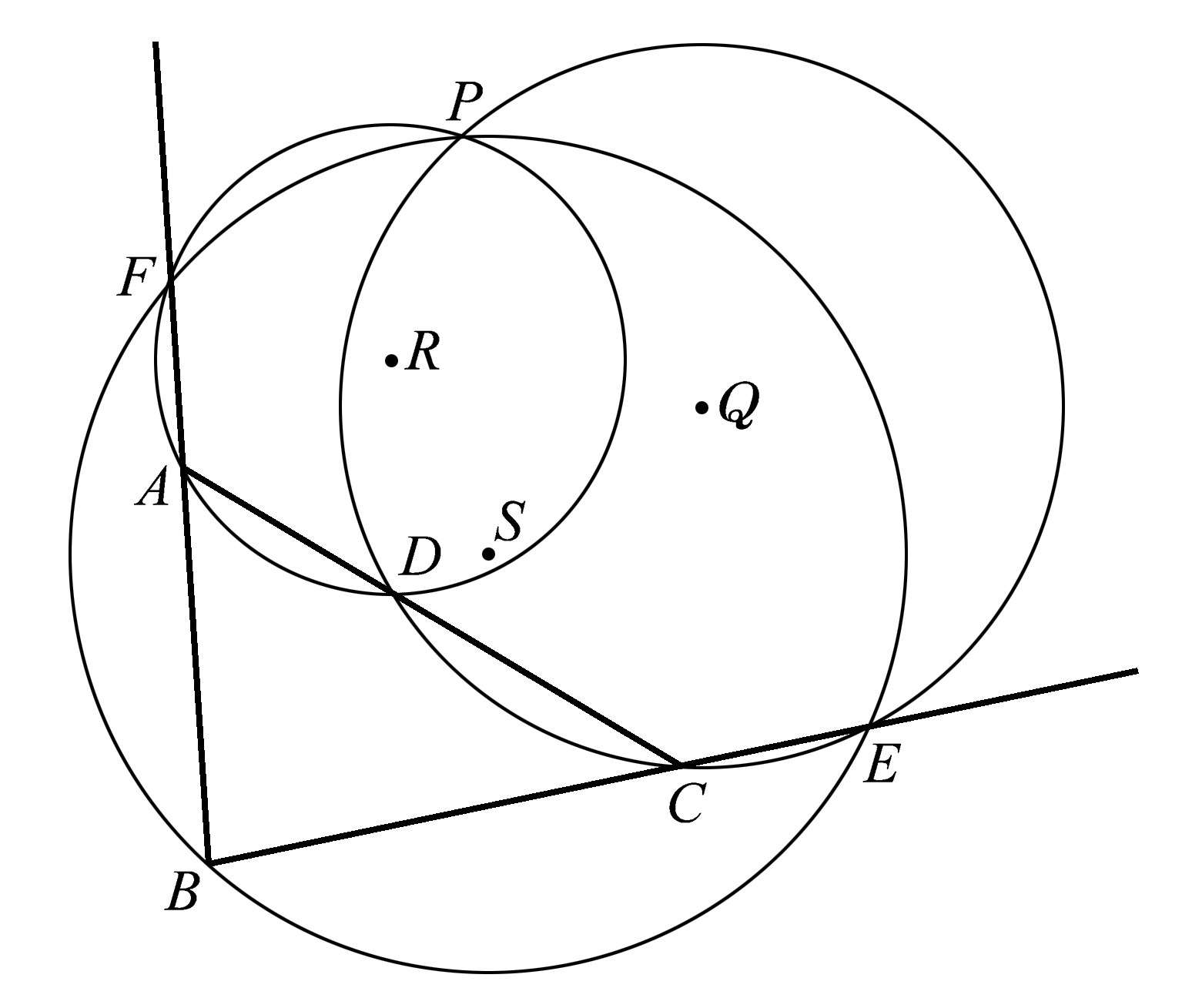
图1.75
我们甚至可以将密克尔定理和共点圆应用于一个四边形。如果我们延长一个四边形的各边,直到相对的边相交(假设它们不平行),那么由此得到的构形称为完全四边形( complete quadrilateral )。与此同时,我们还得到四个三角形,我们在每个三角形上作密克尔圆。神奇的是,我们发现上述所有圆都共点于点 P 。在图1.76中,请注意观察四个三角形△ ABC 、△ ADE 、△ BFE 、△ CDF ,它们的四个外接圆相交于点 P 。
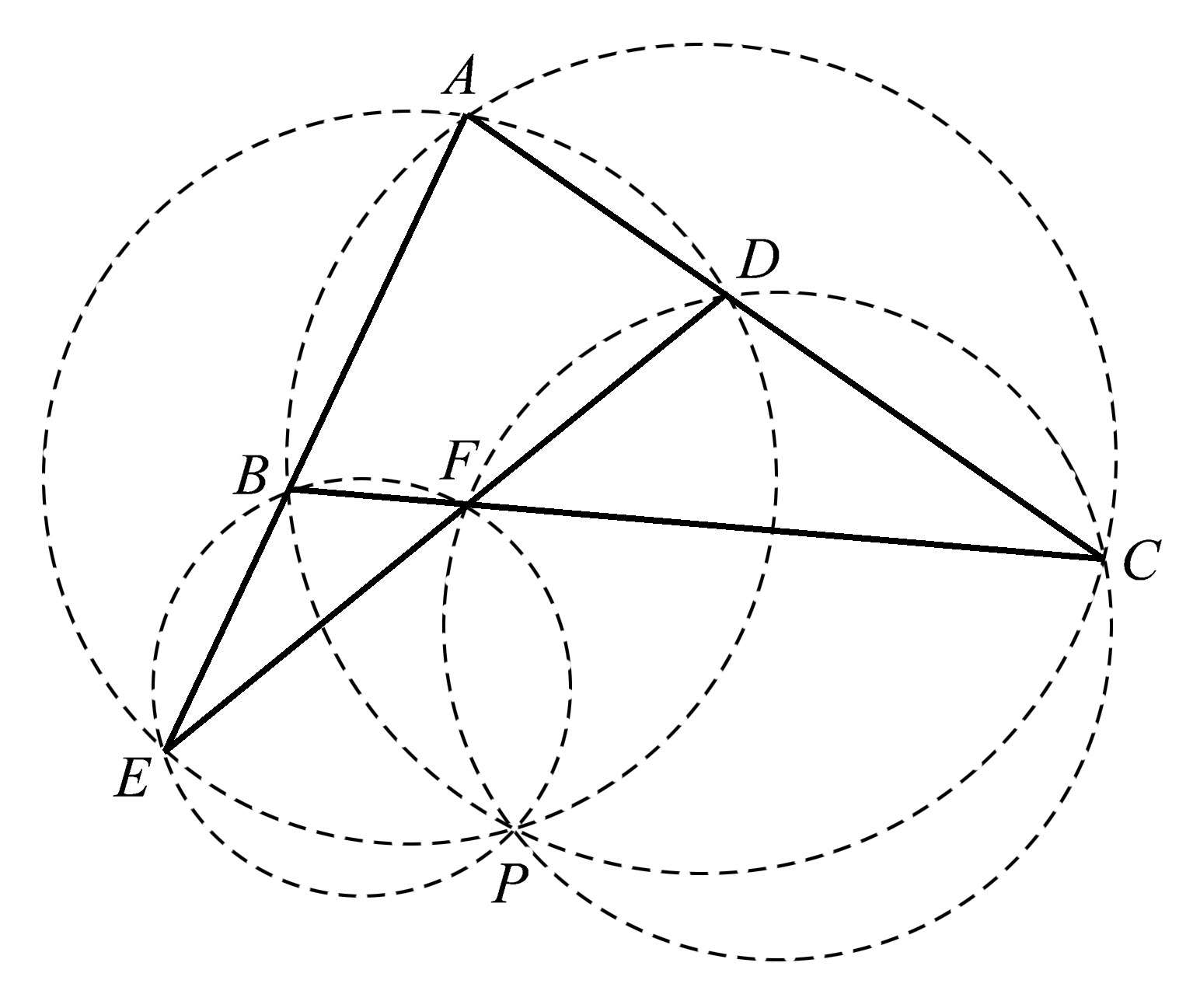
图1.76
不要以为如果没有三角形,三个圆就不能形成共点。如图1.77所示,我们有三个随机的圆,它们都内切于大圆,我们将这些圆的交点标为 D 、 E 、 G 、 F 。当我们分别将各个圆的圆心与其余两个圆的远端交点连接起来时,就会发现它们共点于点 P ,即 DQ 、 ER , FS 是三条共点线。
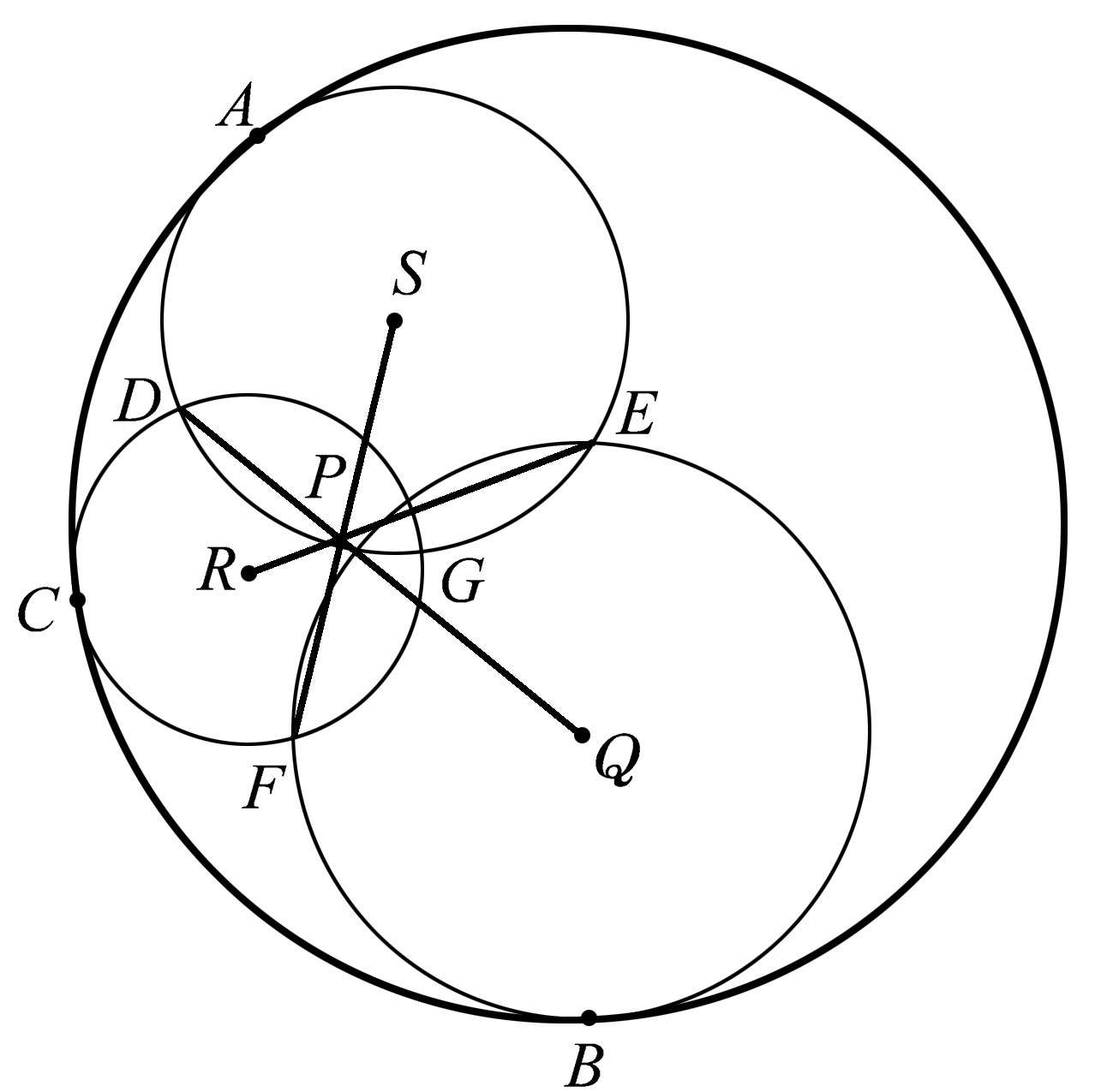
图1.77
现在让我们暂时放下圆,集中讨论直线图形。在这里,一个相当简单的作图会衍生出一个十分意想不到的共点性。从任意矩形 ABCD 开始(如图1.78所示),画平行于 AD 的 EJ ,交 AB 、 DC 于点 E 、 J 。同样,再画平行于 AB 的 FK ,交 AD 、 BC 于点 F 和 K 。现在,最意想不到的结果出现了:作矩形 ADJE 的对角线,然后作矩形 FDCK 的对角线。当我们继续作矩形 ERKB 的对角线并延长时,可以发现这三条对角线共点于点 P 。这个结论对于任何矩形都适用。如图1.78、1.79、1.80所示,这三个不同的矩形都得出同样的结论。
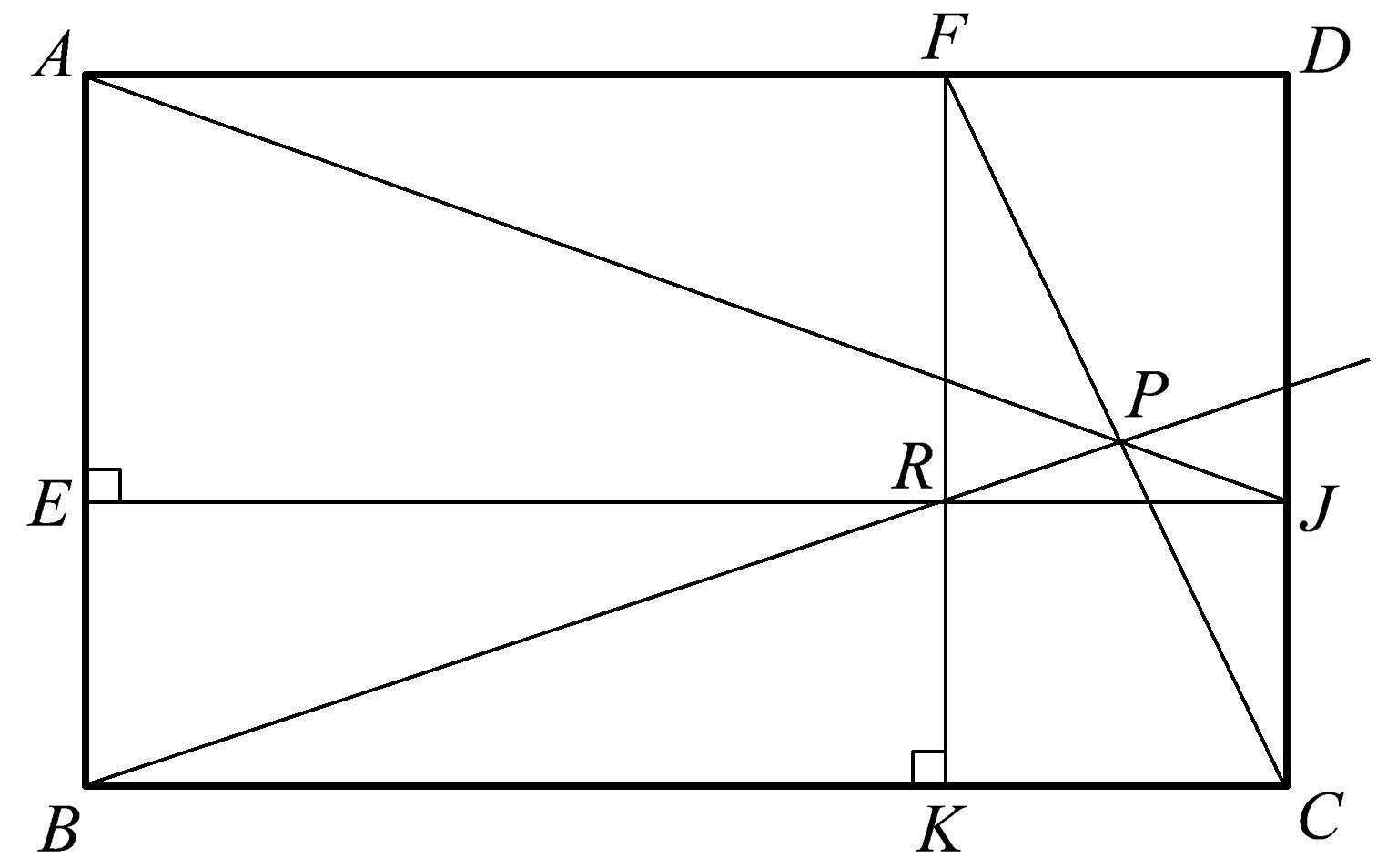
图1.78
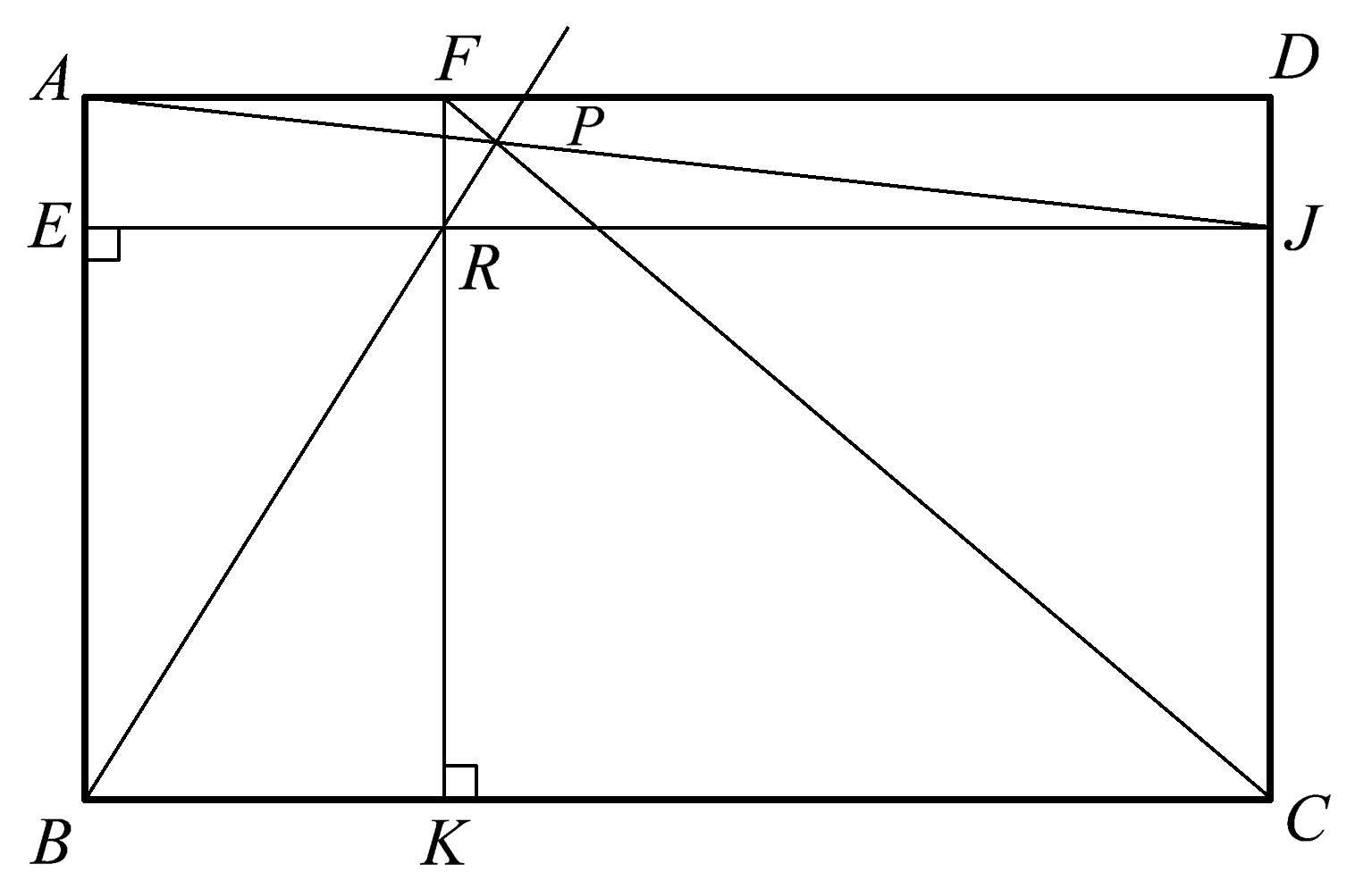
图1.79

图1.80
如果我们随机选取任意三角形(如图1.81所示的三角形 ABC ),并在其两条边(图中的 AB 边和 BC 边)的外侧作正方形,就会得到一个神奇的共点。我们从其中一个正方形的远端顶点向三角形 ABC 的最远边作一条垂线,即图中的 DK , DK 垂直于 BC 。然后我们对另一个正方形进行同样操作:作 FL 垂直于 AB 。这两条垂线相交于点 P 。出人意料的是,当我们从点 B 作 AC 边上的高时,我们发现此高与前两条垂线是共点的。

图1.81
我们作进一步扩展:在现有的两个正方形外侧分别添加一个与之全等的正方形,如图1.82所示。连接新正方形和三角形的两对远端顶点得到的两条线 TC 、 VA 与从点 B 所作的三角形 ABC 的高 BG 是共点的。

图1.82
假设三角形 ABC 是一个直角三角形,顶点 B 处为直角。我们将再次连接三角形和正方形的两对远端顶点,如图1.83中的线段 DC 和 AF 所示。令人惊讶的是,它们与从点 B 到斜边 AC 的高相交于点 P 。我们再次得到了三条共点线——相当神奇!
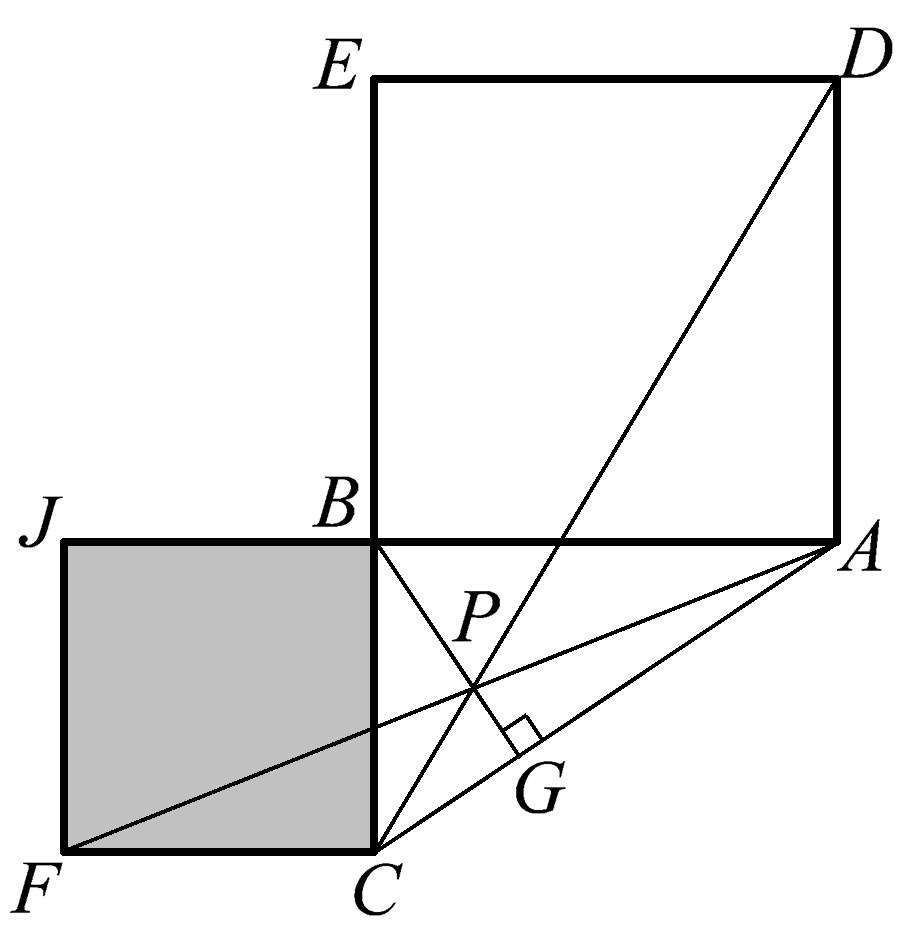
图1.83
这一次,我们在三角形 DEF 的每条边外侧各作一个正方形,再延长这三个正方形的外侧边,构成三角形 ABC ,如图1.84所示。当我们连接 AD 、 BE 、 CF 并延长时,我们发现它们共点于点 P 。
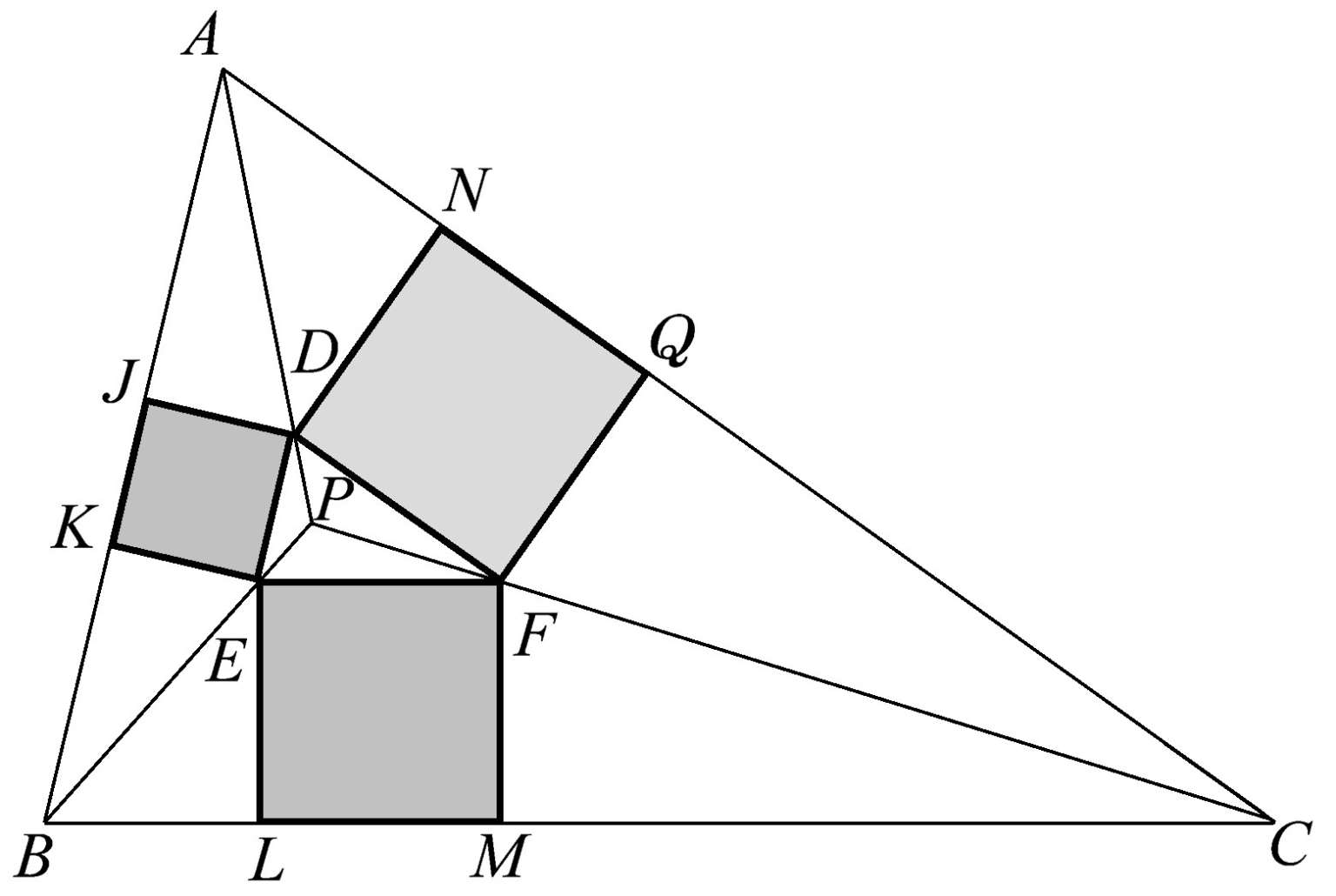
图1.84
在三角形的外侧作正方形,我们还可以发现许多共点性。在图1.85中,三角形 ABC 是任意的锐角三角形,每个正方形的对角线交点就是其中心,把每个正方形的中心和距其最远的三角形顶点连接起来,我们发现 AS 、 BQ 、 CR 这三条直线是共点的。请记住,与前述那些例子一样,这个共点性与三角形的形状无关。这就是我们想要展示的几何之美。

图1.85
我们可以用一些颇具创意的方法来发现更多的共点性。图1.86展示了四条直线交于一点的一个特殊构形。其中 AF 和 CE 分别是三角形 ABC 的两个顶点 A 、 C 与其对边外侧的正方形远端顶点 F 、 E 的连线。 DG 是上述两个正方形的两个远端顶点 D 、 G 的连线。 BQ 是三角形的第三个顶点 B 与其对边外侧正方形的中心 Q 的连线,以上四条线共点于点 P 。这是一个很难被发现的共点性,而这正是我们欣赏它的原因。
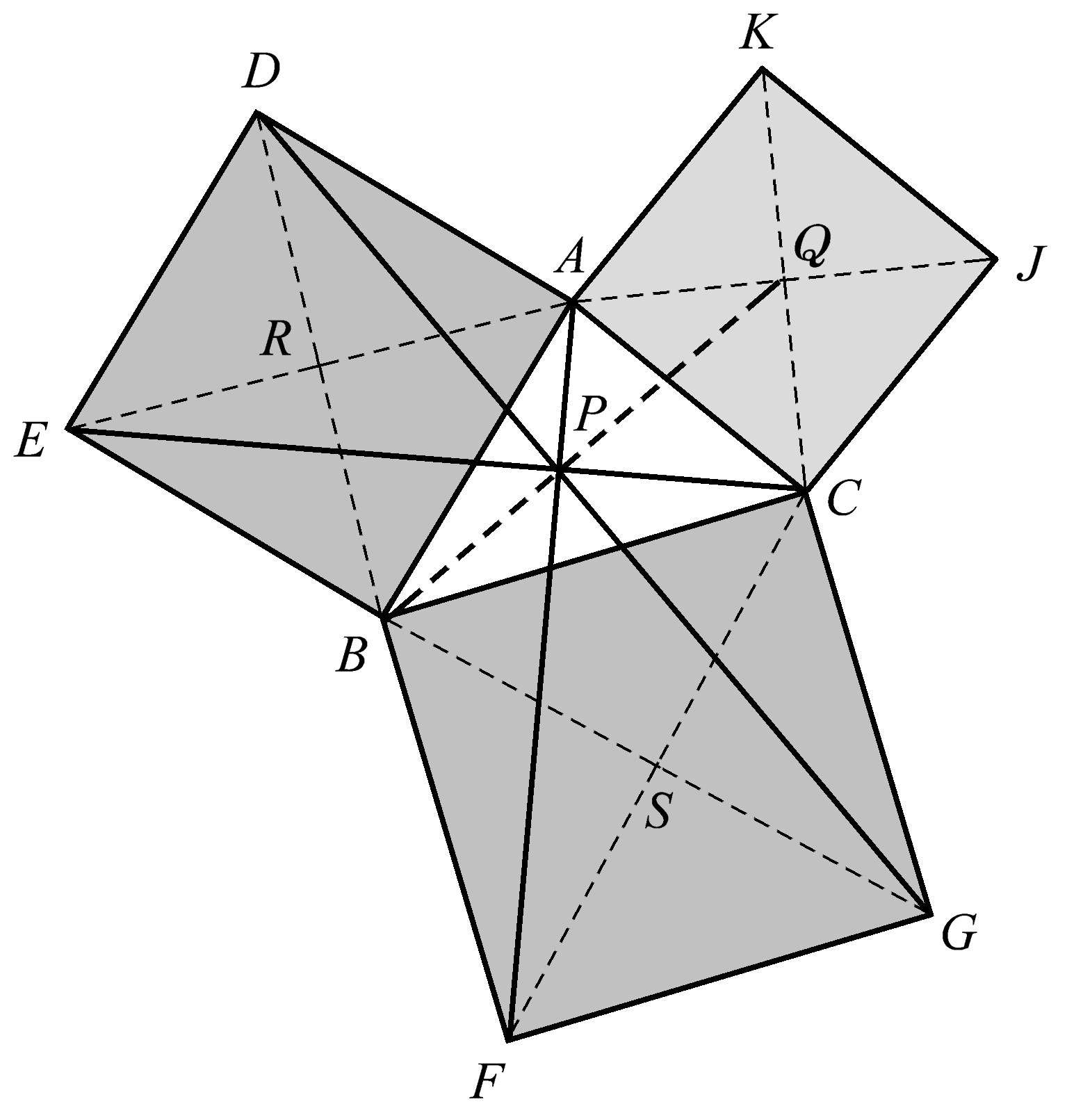
图1.86
有时我们可以在一个构形的局部发现共点性。如图1.87所示,在这里我们可以忽略正方形 BCGF ,仅考虑其余两个正方形。我们发现线段 EJ 、 BK 、 DC 共点于点 P 。显然,我们还可以忽略另一个正方形,然后用其余两个正方形重复这个操作。这正是其美妙之所在。

图1.87
在一个任意三角形每条边的外侧各作一个正方形,这个构形中还藏着许多的共点性。图1.88显示的虽然不是共点性,但也是一种不寻常的情况。将两个正方形的中心相连,得到线 RQ ,再将这两个正方形的公共顶点 A 与第三个正方形的中心 S 相连线,我们发现这两条线段不仅互相垂直,而且长度相等,即 RQ ⊥ AS , RQ = AS 。同样奇妙的是,这个规律对任何三角形都适用。
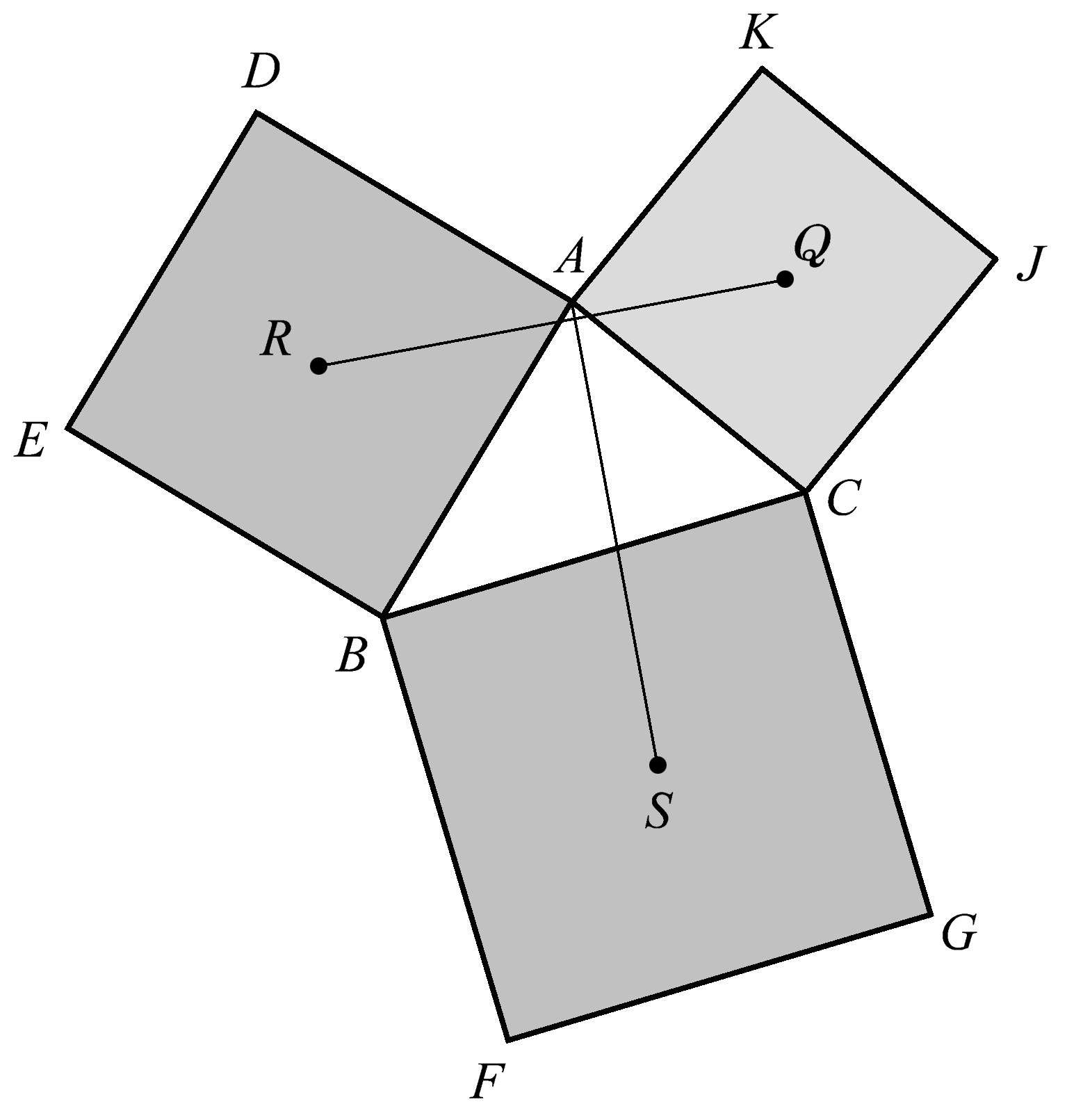
图1.88
图1.89展示了这个构形的又一个共点性。图中, EC 和 JB 与从顶点 A 到边 FG 的垂线共点。
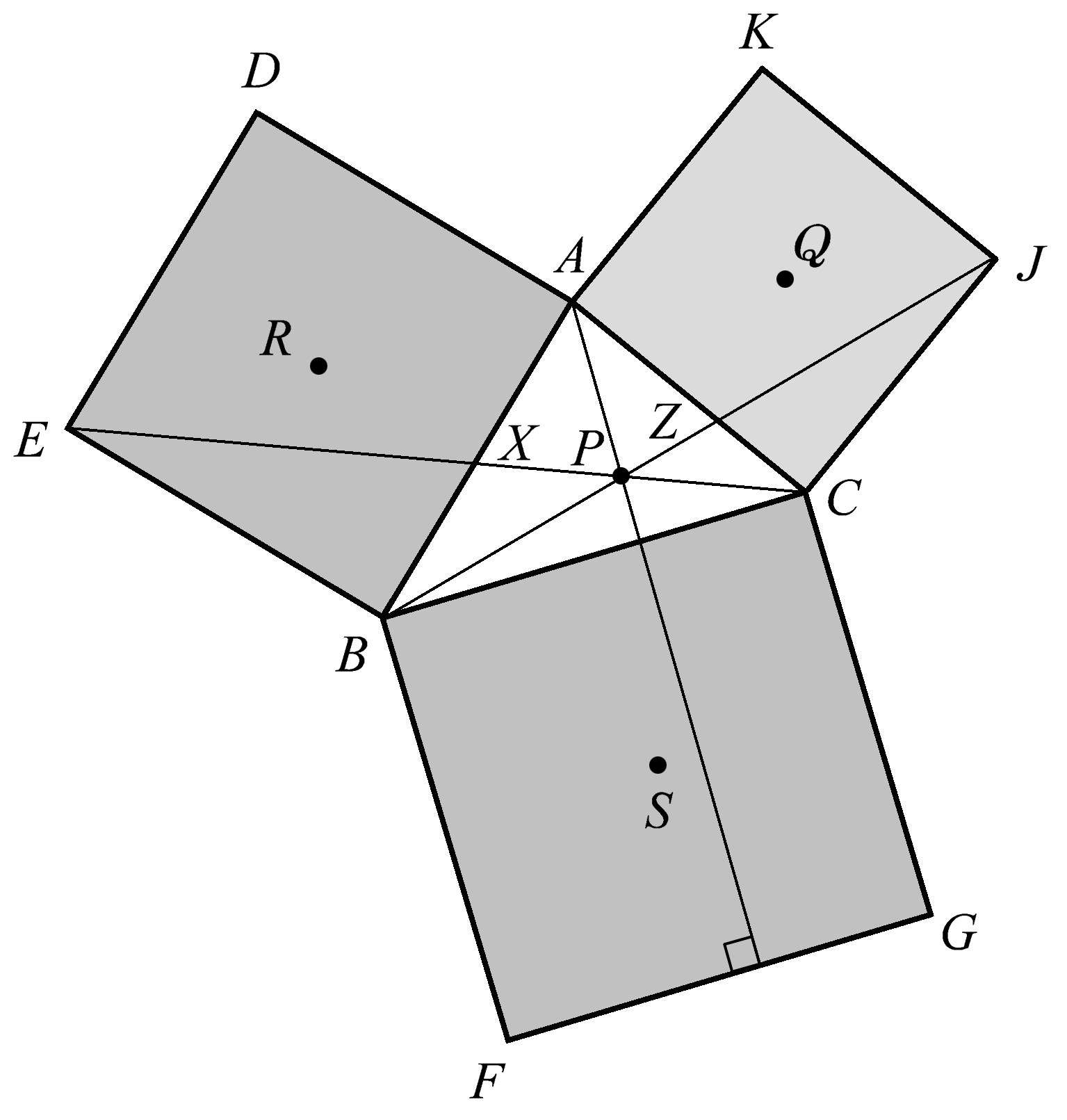
图1.89
现在,为了得到更多的结果,我们在图1.89中的相邻两个正方形之间作平行四边形。这样我们就得到了以下平行四边形: AKXD 、 CJZG 、 BFWE 。通过作对角线来确定每个平行四边形的中心,当我们将平行四边形的中心与远端正方形中心相连时,我们再次惊讶地发现,所得到的 NQ 、 MS 、 RT 共点于点 P ,如图1.90所示。
我们还可以从图1.90中再找到另一个共点性。这一次我们把每个正方形的中心与其对面的平行四边形的远端顶点相连,所得到的 XS 、 WQ 、 ZR 也共点于点 P ,如图1.91所示。
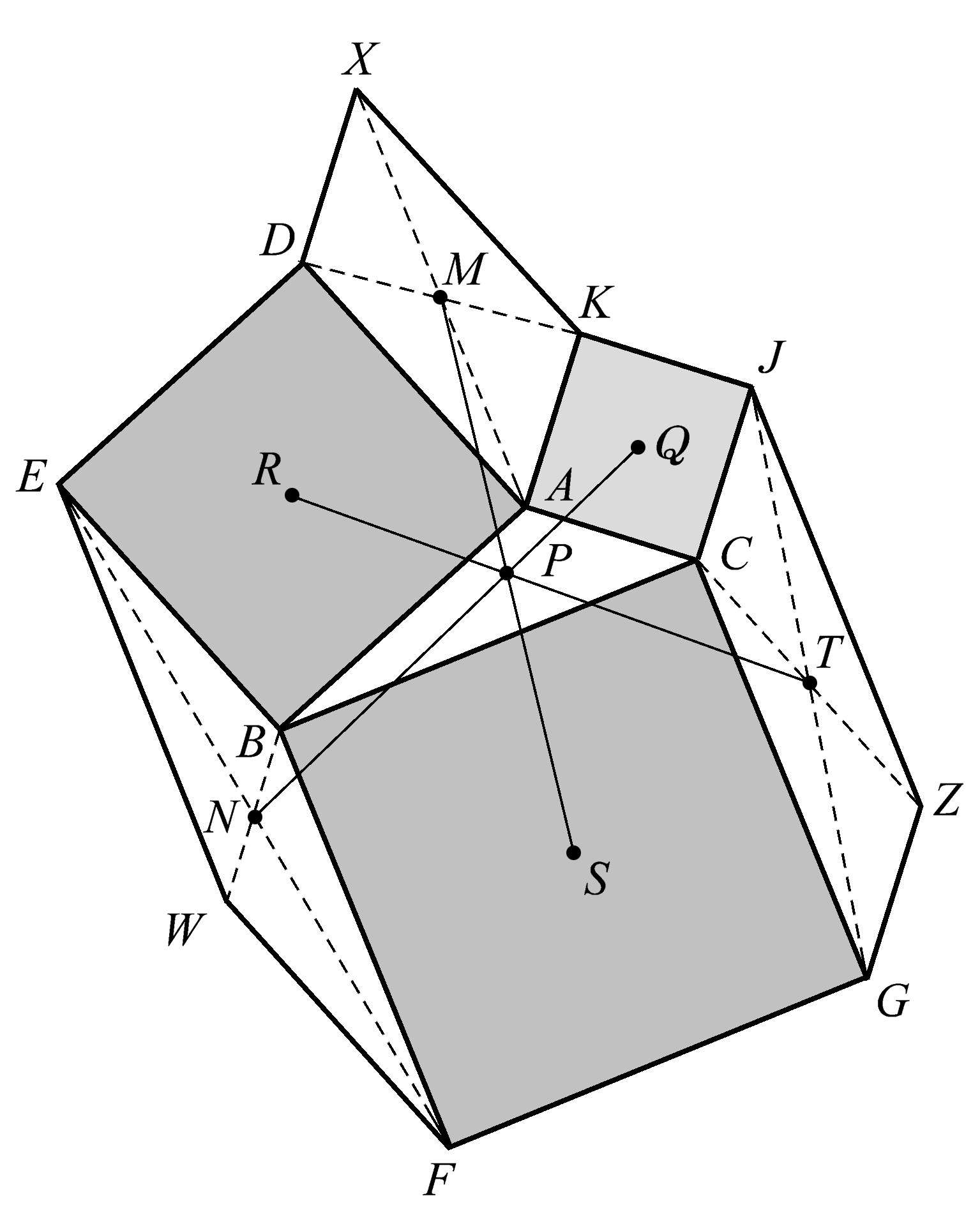
图1.90
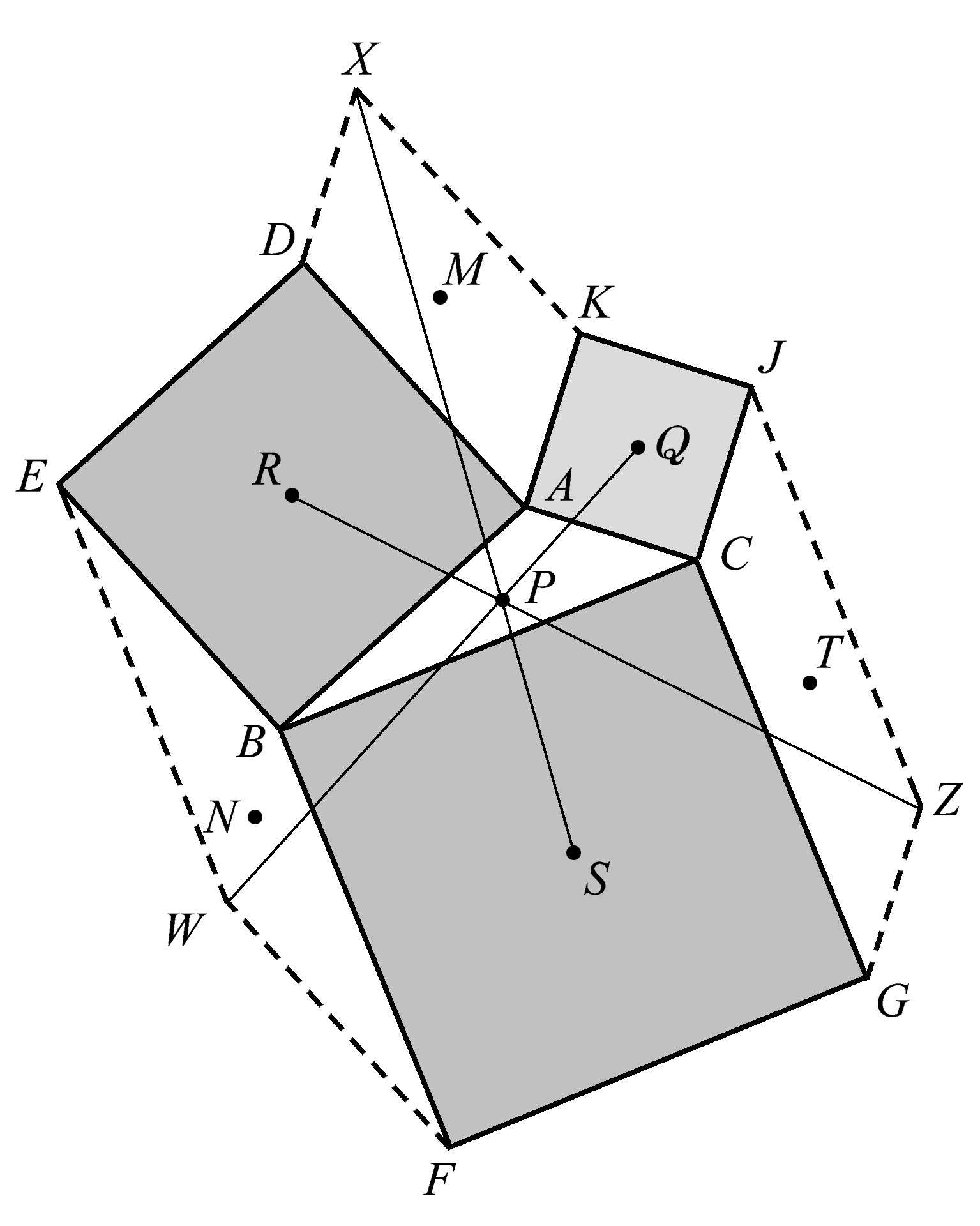
图1.91
在这个构形中还可以找到一个共点性(如图1.92)。将这些正方形的远边 ED 、 KJ 、 FG 的中点 U 、 V 、 Y 分别与其对面平行四边形的远端顶点相连,则 UZ 、 XY 、 VW 也是共点的。
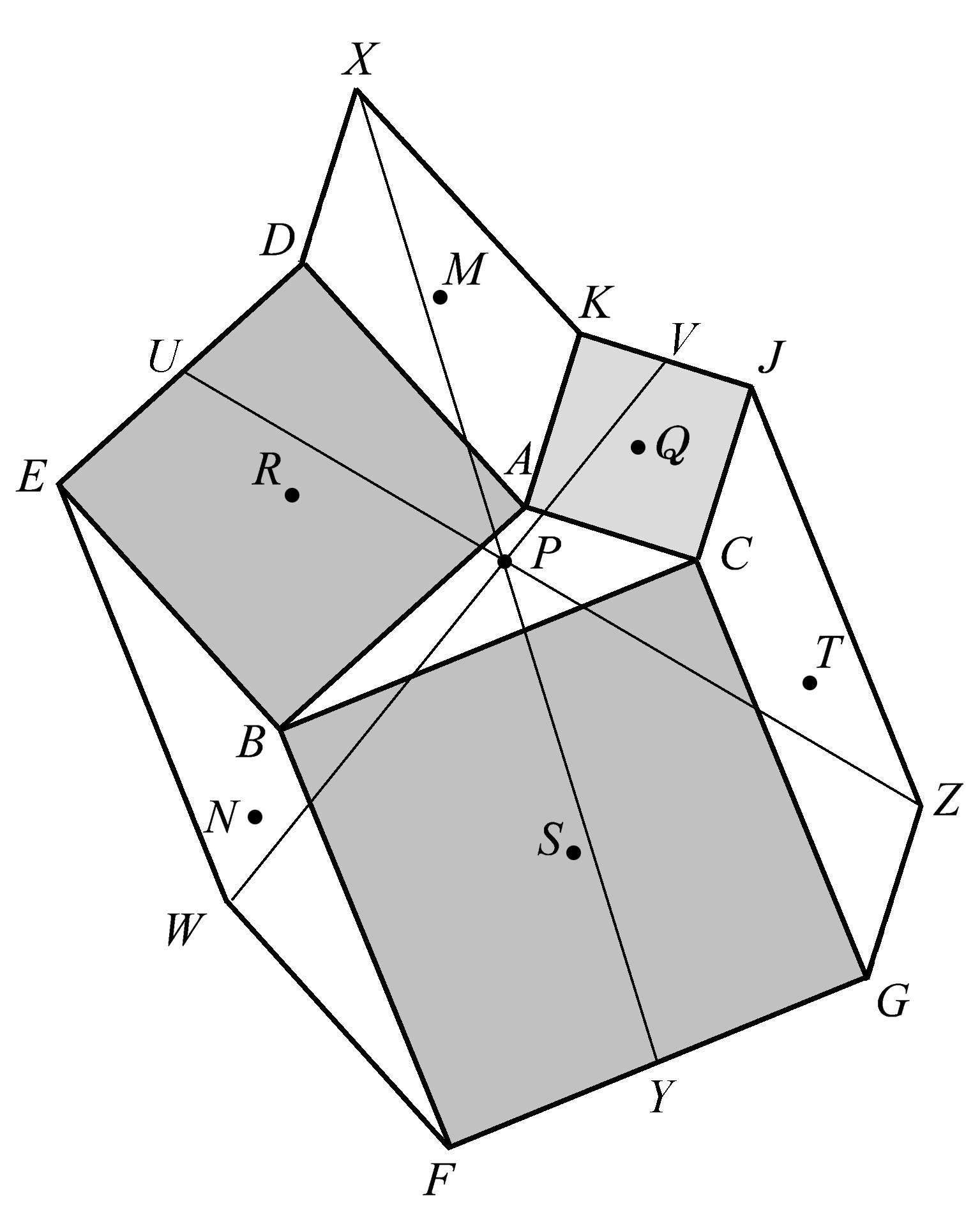
图1.92
在这个构形中,我们还可以找出更多的共点性。这次我们把三角形的各边中点与其对面平行四边形的中心相连,如图1.93所示,则 ML 、 TH 、 NI 共点于点 P 。
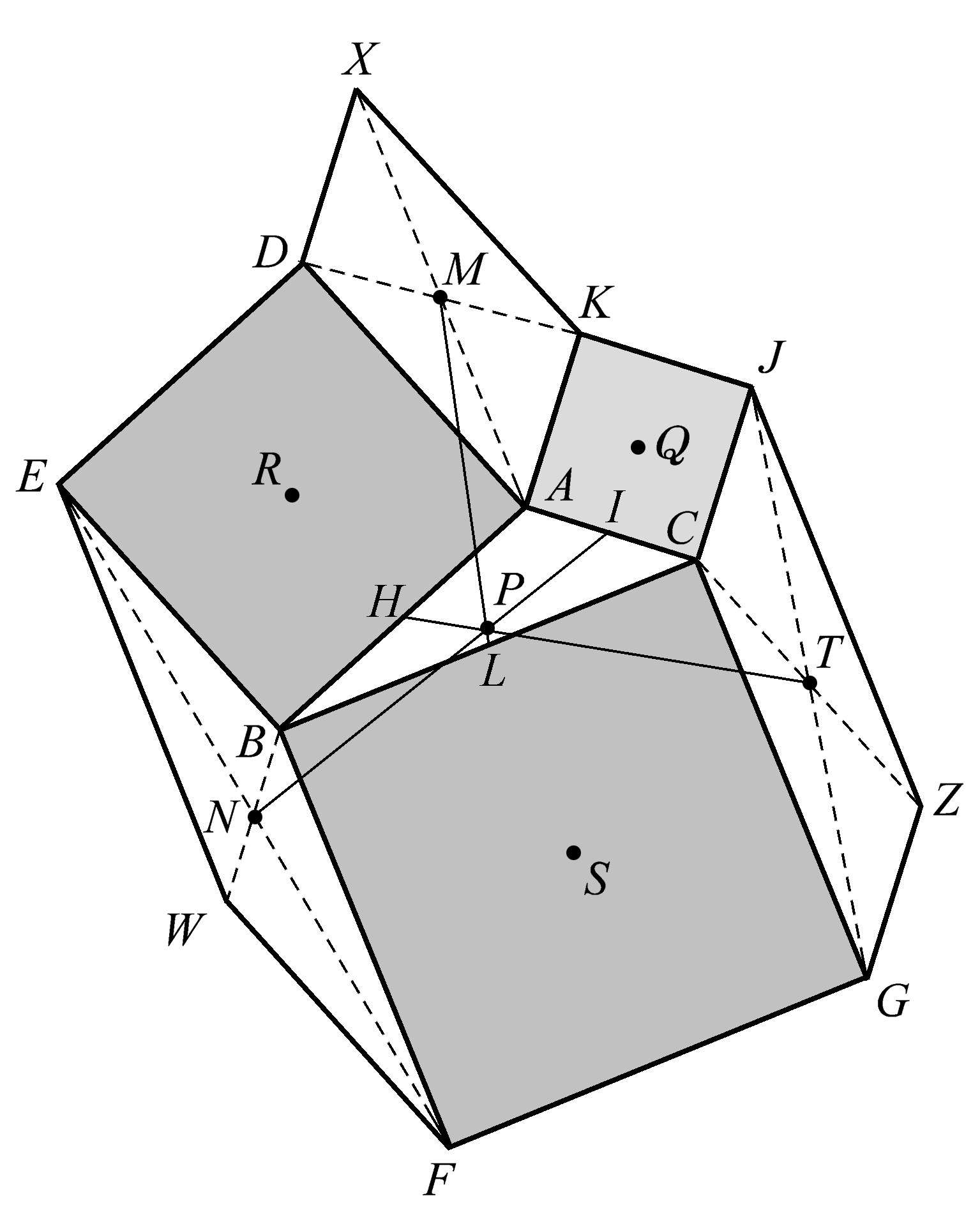
图1.93
同样基于这个构形,我们从三角形 ABC 的每个顶点向以它为顶点的那个平行四边形的对角线作一条高,又能得到一组共点线。延长 NB 、 TC 、 MA ,它们相交于点 P ,如图1.94所示。
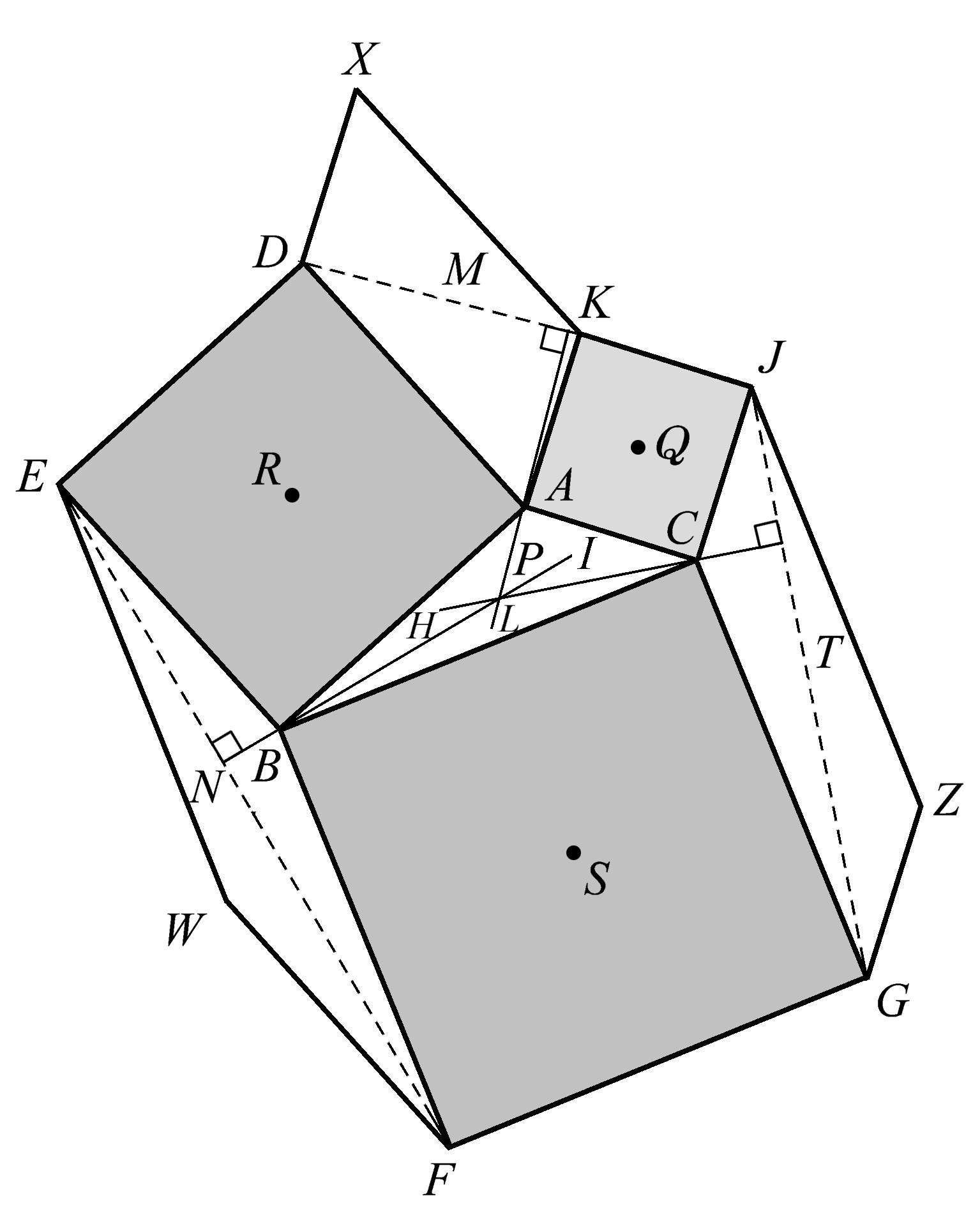
图1.94
作平行四边形对角线的垂直平分线,我们就会得到更多的共点线,如图1.95所示, HM 、 IT 、 LN 三线共点,其中 M 、 N 、 T 是相应的对角线中点。
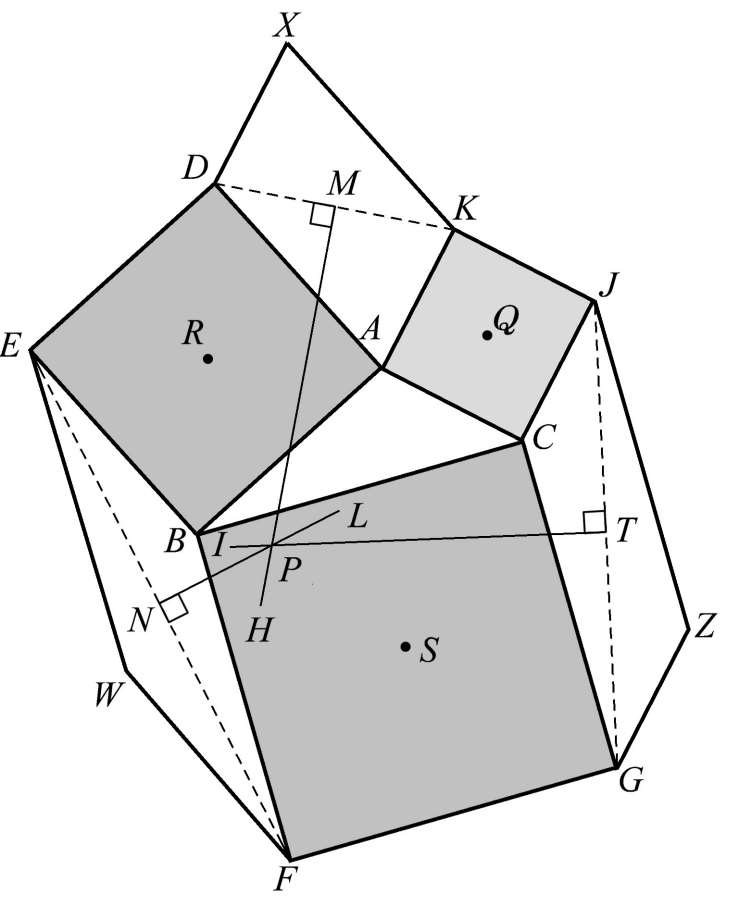
图1.95
在此构形中,除了各种共点性之外,还存在一些相等关系。我们在这里只举一例:在图1.96中,我们注意到 AW =AZ 。其余的留待诸位去发现。祝你好运!
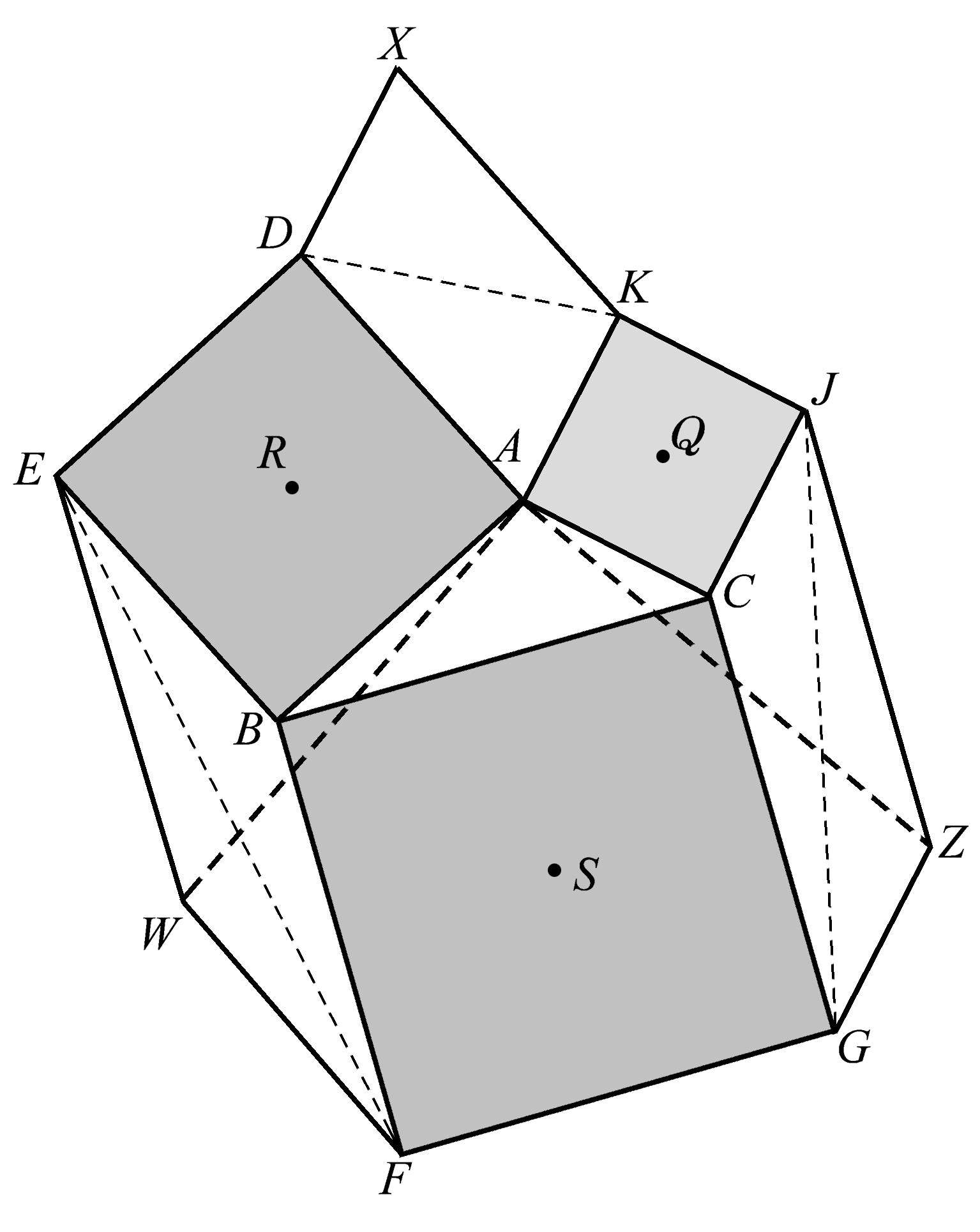
图1.96
我们现在探究在任意四边形 TLUV 外侧作正方形,如图1.97所示。首先,连接相对的两个正方形的中心,得到的 YZ 与 XW 相交于点 P 。奇怪的是,当我们将连接这些正方形相邻顶点的四条线段的中点(点 J 是 AH 的中点,点 K 是 GF 的中点,点 N 是 DE 的中点,点 M 是 BC 的中点)相连时,我们发现 MK 与 NJ 也相交于点 P 。因此,我们得到 YZ 、 XW 、 JN 、 MK 四条线共点于点 P 。

图1.97
我们已经将正方形放在三角形的外侧,然后又将其放在四边形的外侧,现在,把几个正方形围绕一个点排列。如图1.98所示,三个正方形有一个公共点 P 。我们将相邻正方形的相邻顶点用三条线段 AK 、 GF 、 CD 连接起来,再将这三条线段的中点与其对面正方形的中心相连。令人惊讶的是,无论这些正方形的大小和位置如何,只要它们有一个共同的顶点, YM 、 XQ 、 NZ 就总是共点(相交于点 R )。这无疑是一个宝贵的案例!
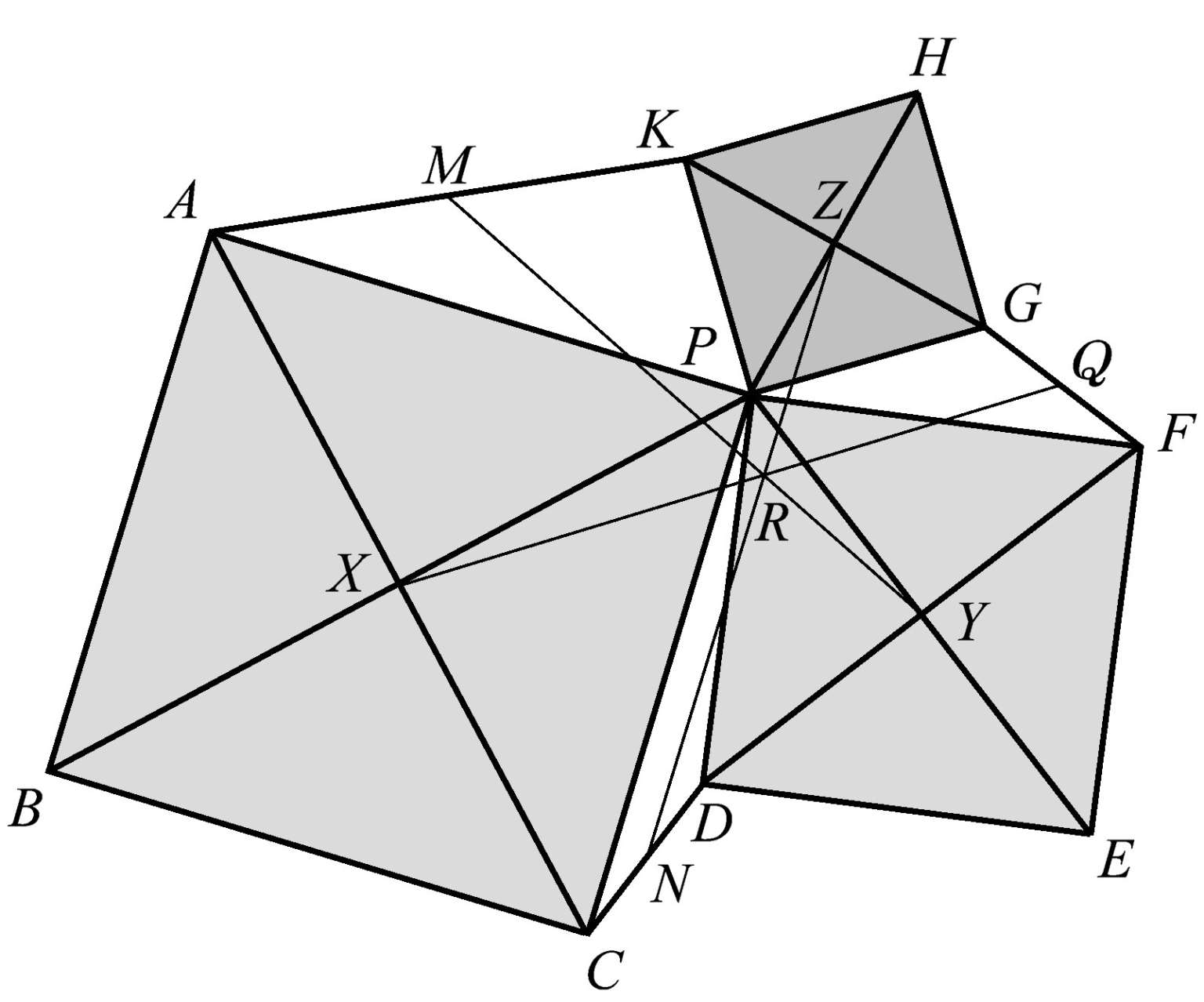
图1.98
假如两个正方形有一个公共顶点,那么我们也能找到一些共点线。在图1.99中,两个大小不同、随机放置的正方形有一个公共顶点 A 。当我们连接 BE 、 CF 、 DG 时,就会发现它们共点于点 P 。与之前的诸多例子一样,无论这两个正方形如何放置都不会影响这一共点性。
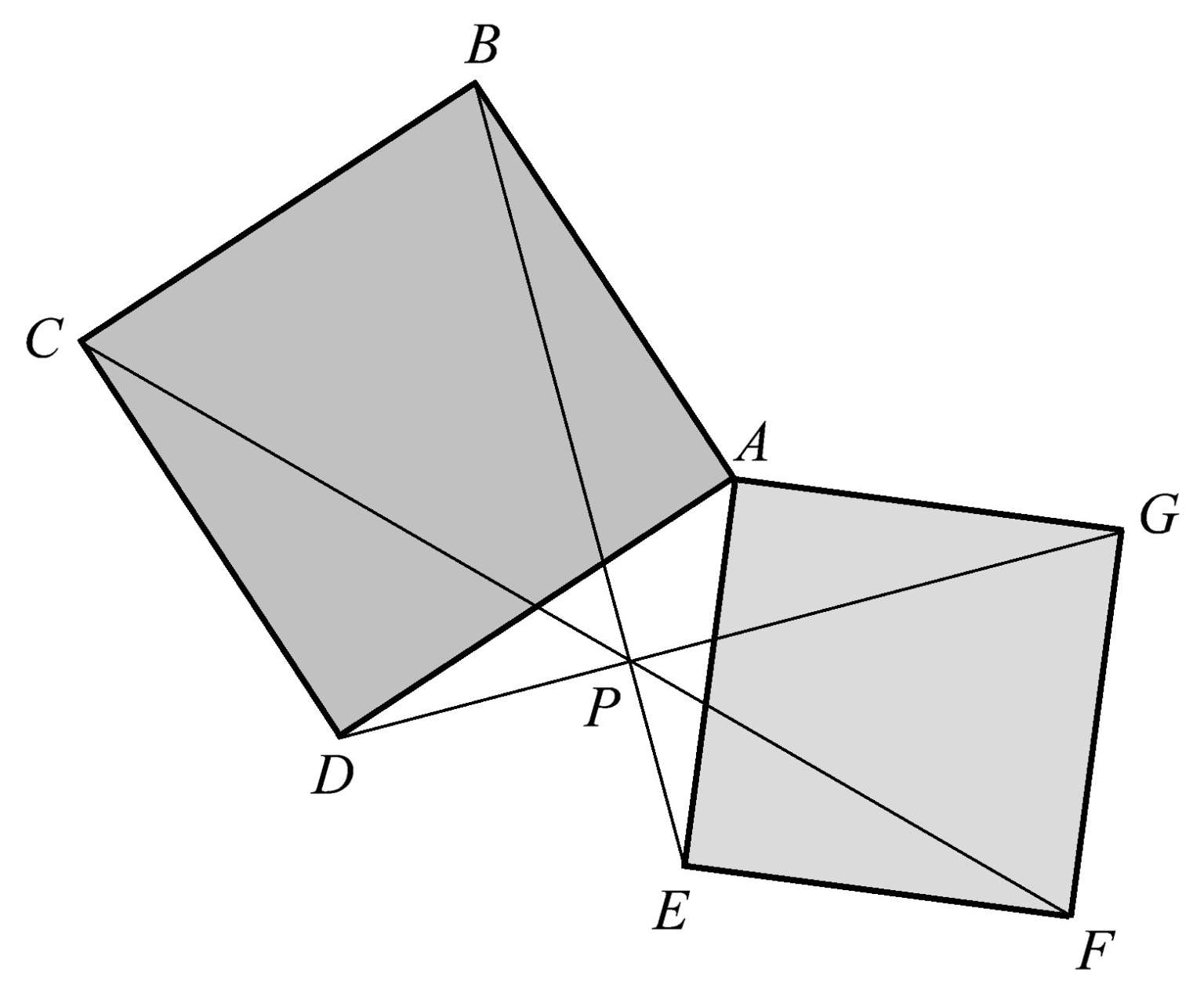
图1.99
为了体现这两个正方形的位置不会影响共点性,我们作图1.100。两个正方形的大小和位置都发生了变化,而共点性仍然保持不变。
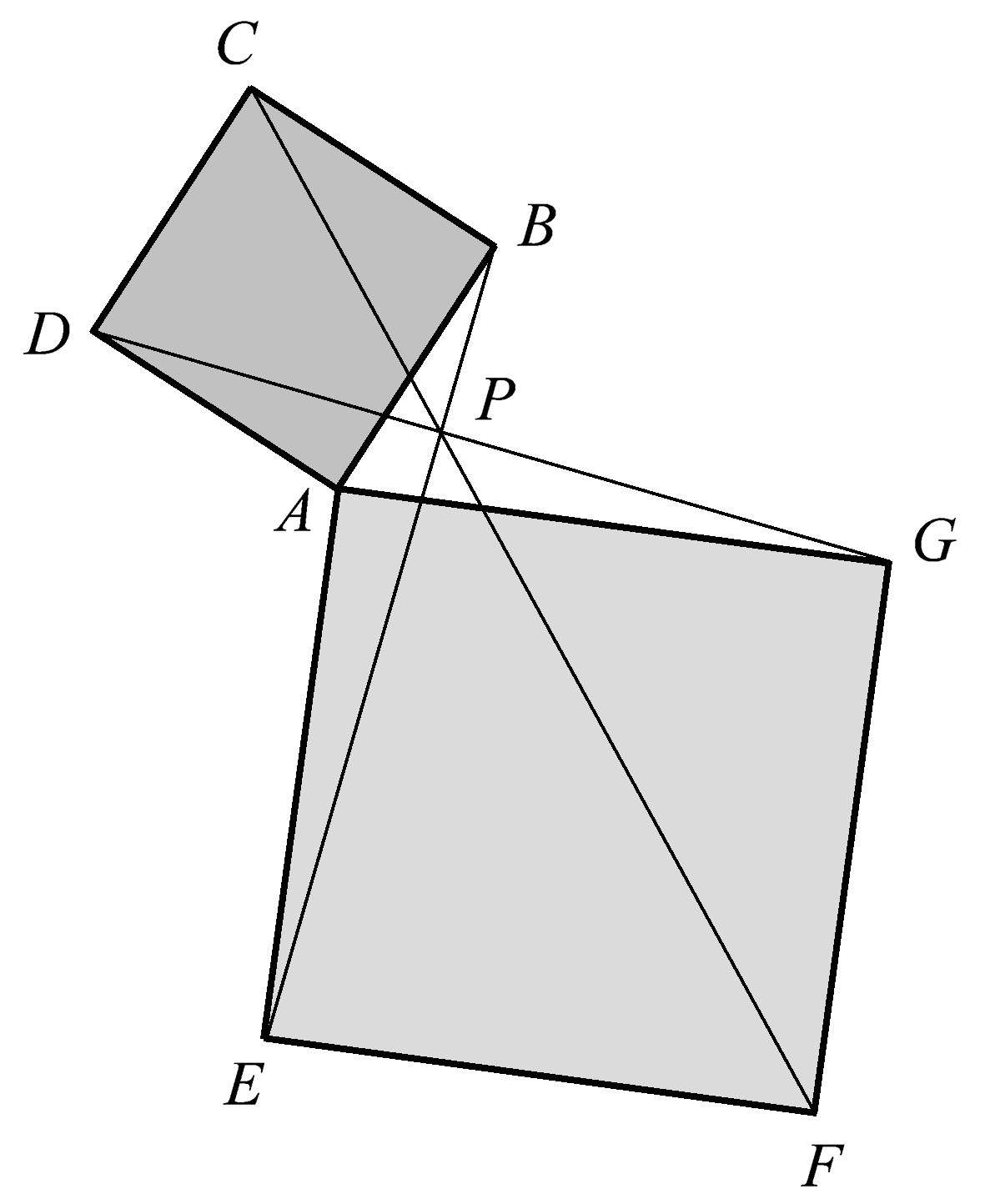
图1.100
此外,还可以将多边形放在三角形的各边上。例如,图1.101中, P 为三角形 ABC 内的任意一个点,将点 P 与三个顶点相连,并构建平行四边形,如图所示。当我们将三角形 ABC 的每个顶点连接到以其对边为对角线的那个平行四边形的远端顶点时,可以发现 AF 、 BE 、 CD 共点于点 R 。除了这个已经很令人惊叹的共点性之外,对于求知欲极强的读者,我们再多提供一点信息: AF 2 + BE 2 + CD 2 = ( AB 2 + BC 2 +AC 2 ) + ( AP 2 + BP 2 + CP 2 )。
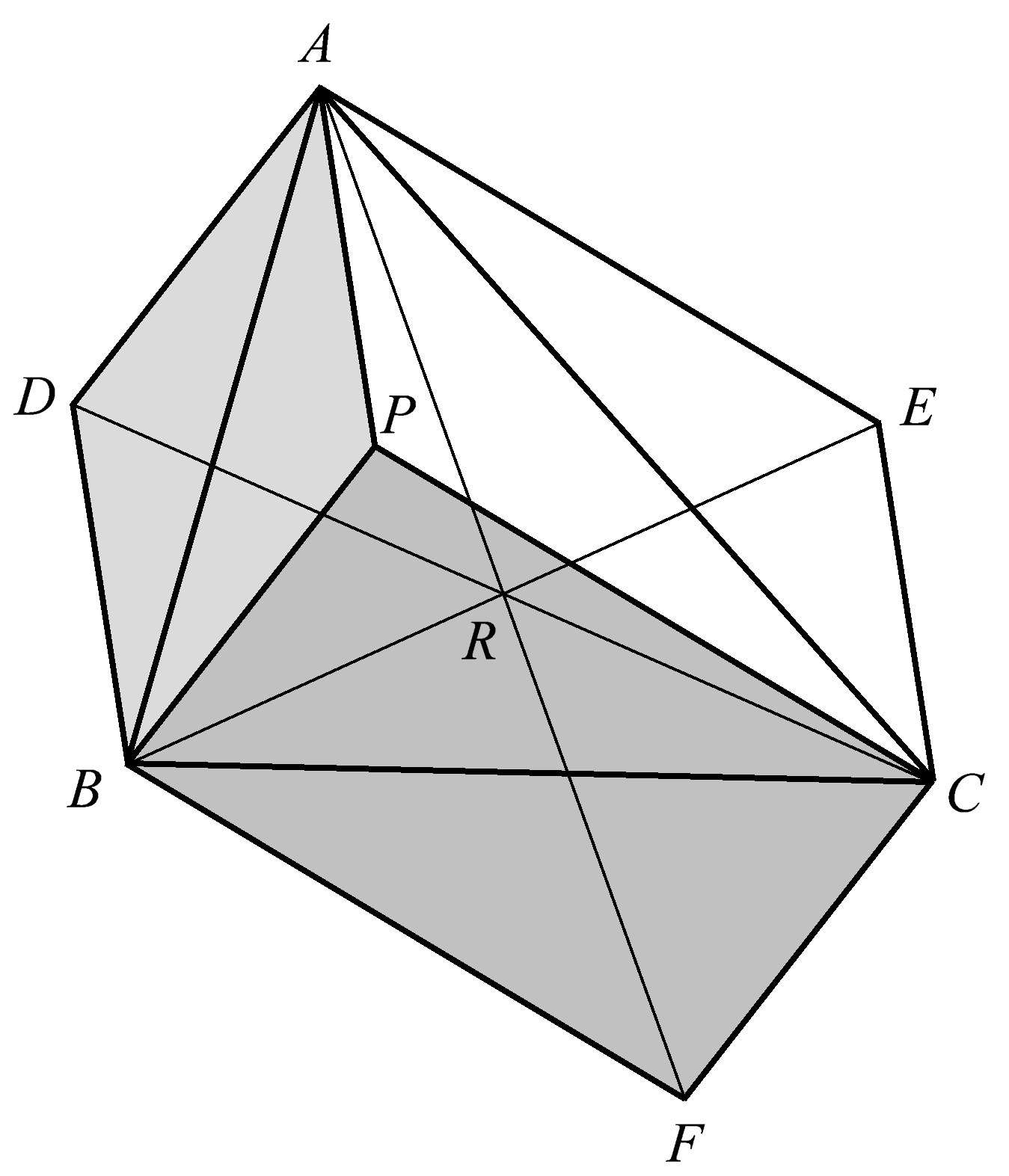
图1.101
我们可以任意放置两个正五边形,只要确保它们有一个公共顶点,就可以发现一些惊人的共点性。在图1.102中,两个正五边形的公共顶点是 X 。当我们将它们的对应顶点相连时,得到的 AE 、 BF 、 CG 、 DH 共点于点 P 。点 P 的位置可能在任何地方,这取决于五边形的大小和位置。

图1.102
用六边形来代替五边形,并重复这个方案,我们仍然能找到相应的共点性。在图1.103中,有两个六边形,它们有一个公共顶点 N ,除此之外它们是随意放置的,且大小不同。连接对应的顶点,可以发现 AF 、 BG 、 CH 、 DJ 、 EK 这五条直线共点于点 P 。
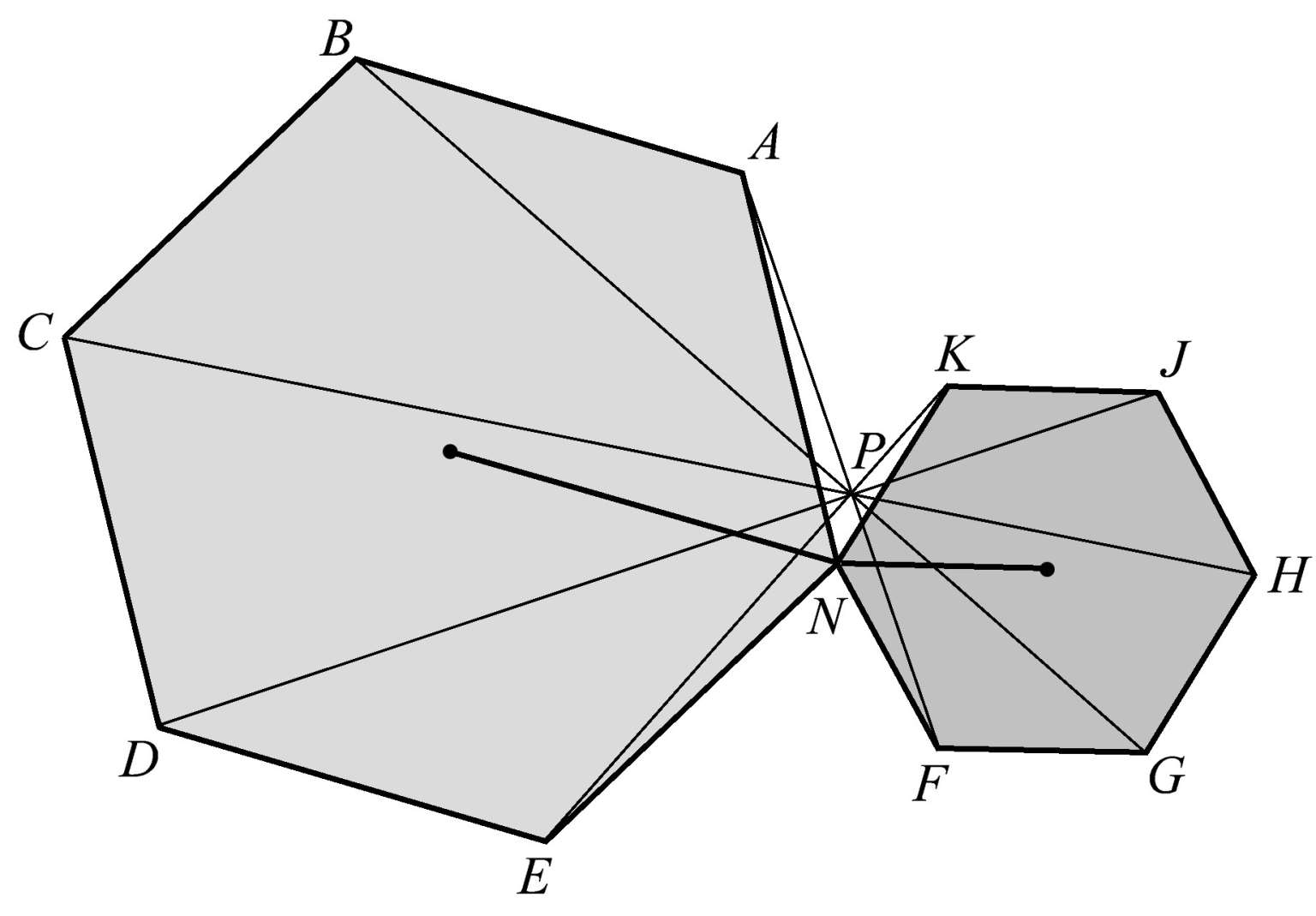
图1.103
我们来寻找更多的共点性,如图1.104所示,正方形 DEFG 位于三角形 ABC 的内部,且正方形的两条边平行于三角形的高 AH 。当我们作直线 BFJ 和 CGK 时,再次发现了一个意想不到的共点性,这两条线与高 AH 共点于点 P 。同样,关键在于三角形和正方形的位置,而不是它们的大小。多么美妙啊!
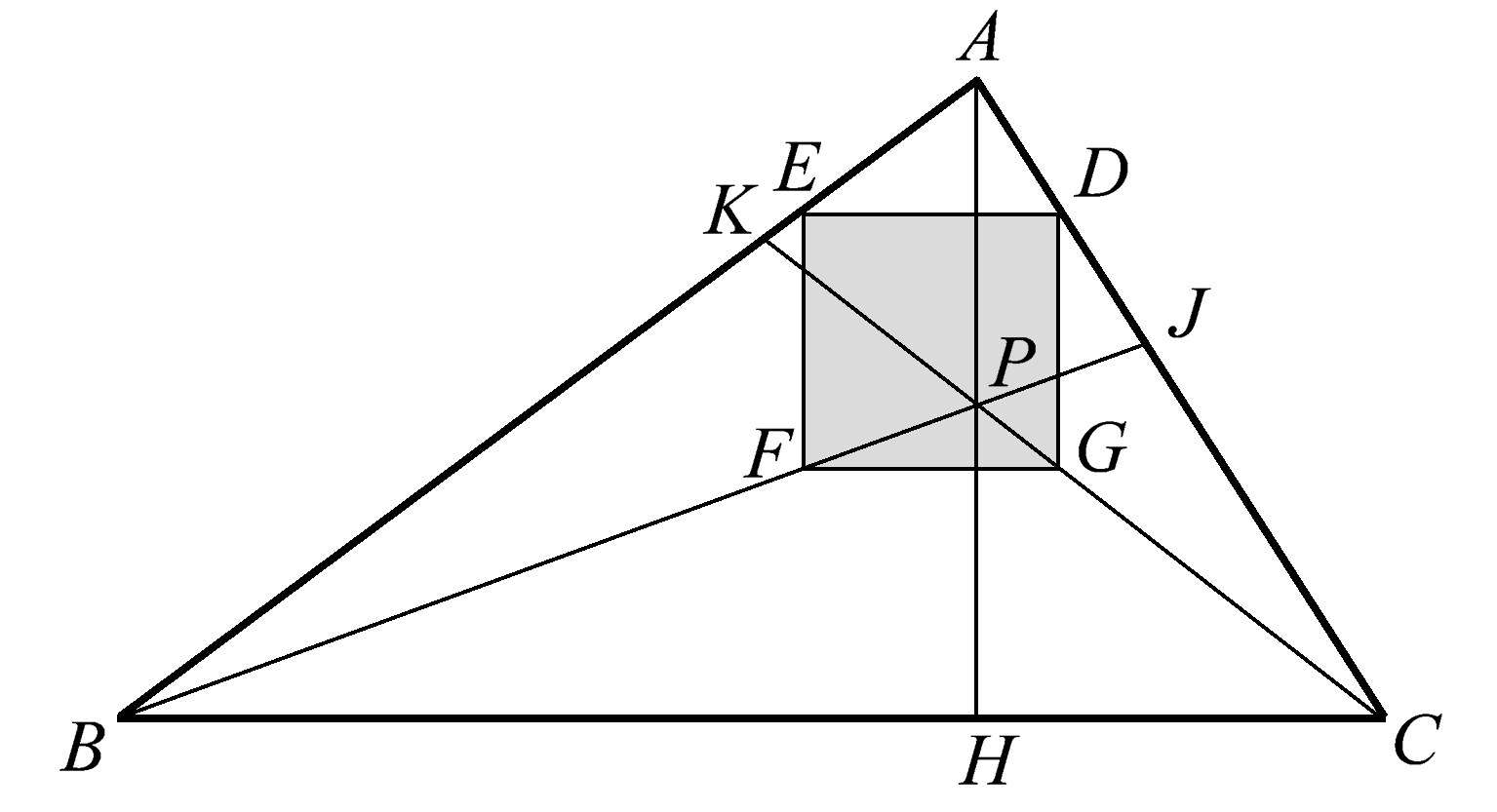
图1.104
对于那些习惯于处理相似三角形的人来说,有一个案例相当特别。考虑两个非全等的相似三角形,小的位于大的里面,并且两者的对应边平行,如图1.105所示,三角形 ABC 的各边与三角形 DEF 的相应各边平行。我们可以清楚地看到,连接对应顶点的各直线共点于点 P 。

图1.105
另一种嵌套三角形的方法是:从大三角形的每个顶点向距该顶点最近的小三角形的边作垂线。你会再次发现这些垂线是共点的。
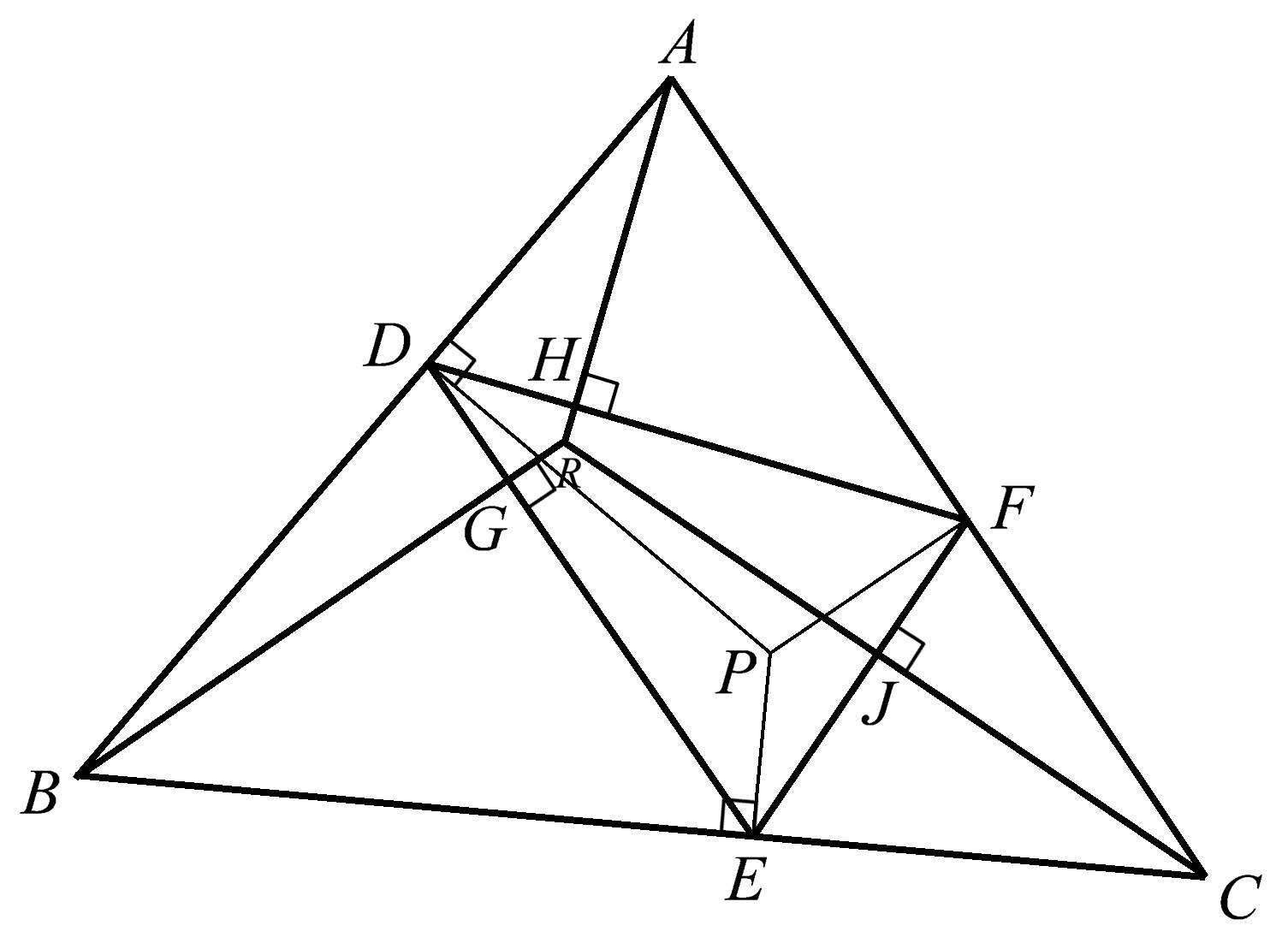
图1.106
如图1.106所示,其中三角形 DEF 的每个顶点都位于三角形 ABC 的边上,从大三角形的顶点 A 、 B 、 C 分别向边 DF 、 DE 、 EF 作垂线,垂足分别为点 H 、 G 、 J 。这三条垂线 AH 、 BG 、 CJ 共点于点 R 。
如果这还不够令人印象深刻,我们可以更进一步展示此构形的另一个共点性。过点 D 、 E 、 F 作三角形 ABC 各边的垂线,这三条垂线将共点于点 P (图1.106)。
我们的下一个例子将展示两个内接于同一个圆的三角形是如何通过它们的角平分线和高建立联系的。图1.107显示了三角形 ABC 及其外接圆 O 。我们作三角形 ABC 的各个内角的角平分线,与外接圆相交于点 D 、 E 、 F 。结果表明,这些角平分线的交点 I 也是三角形 DEF 的垂心。换言之,点 I 也是三角形 DEF 的高 DX 、 EY 、 FZ 的交点。因此,我们可以说,这两个三角形通过角平分线和高而建立了联系。
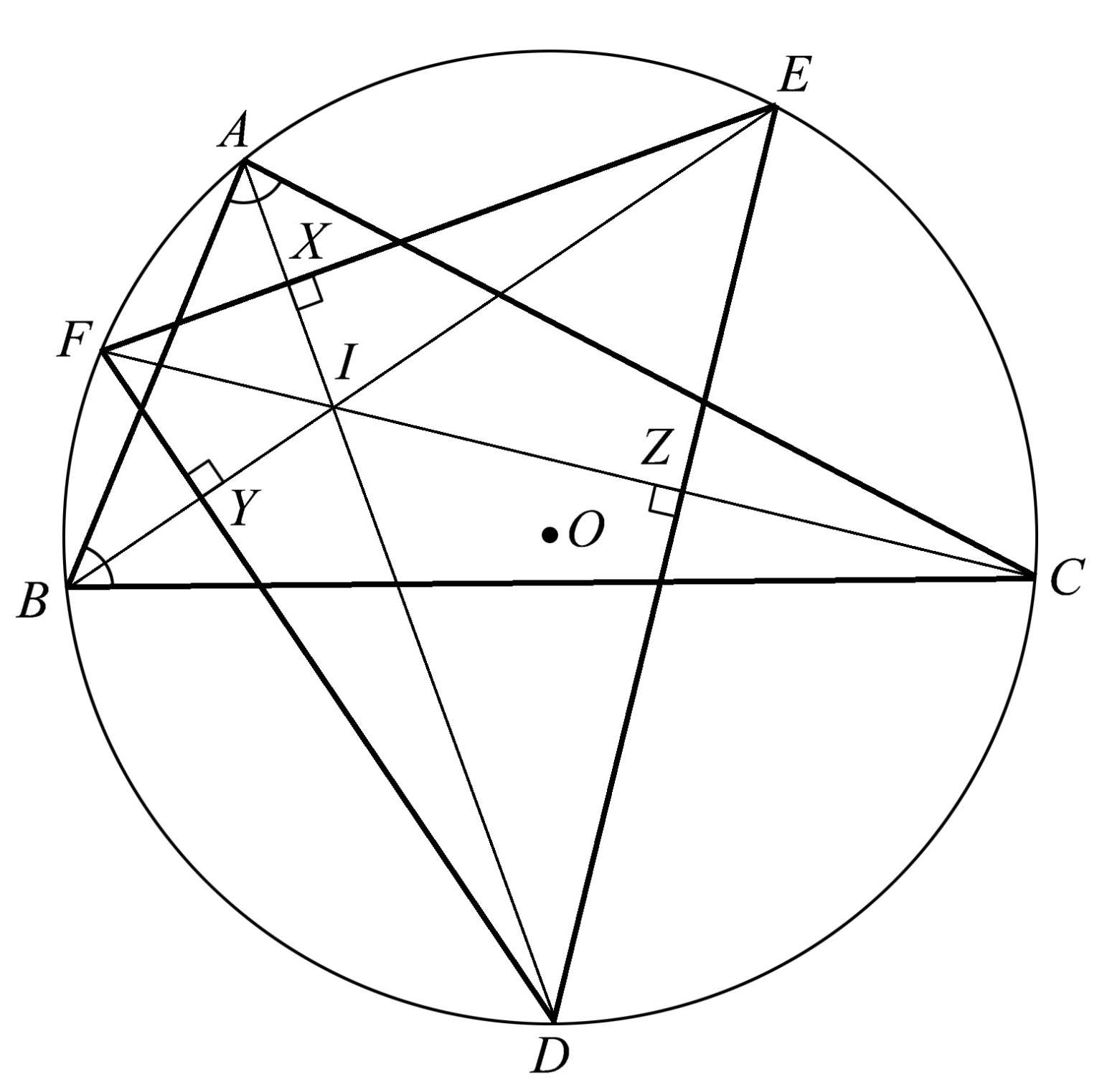
图1.107
下一个构形虽然有些复杂,但它再次以一种让人意想不到的方式显示出共点性。我们从三角形 ABC 及其内切圆 O 开始,如图1.108所示。首先,我们作圆 O 的任意一条直径,并从三角形 ABC 的每个顶点出发,作该直径的垂线,与这条直径分别相交于点 D 、 E 、 F 。然后我们从 D 、 E 、 F 这三个点出发作另一组垂线,它们分别垂直于三角形的三条边 BC 、 AC 、 AB ,垂足分别为 P 、 Q 、 R 。神奇的是,我们发现 EQ 、 FR 、 DP 共点于点 X 。这一构形再次展现了几何之美,而实现这种美的起点有时却很不起眼。

图1.108
下一个共点性的发现同样复杂。我们从三角形 ABC 开始,如图1.109所示,首先在三角形内部选择任意点 P ,然后过点 P 作一条直线 l ,与三角形各边分别相交于点 X 、 Y 、 Z 。现在使 AP 、 BP 、 CP 的延长线分别与三角形 ABC 的外接圆相交于点 R 、 S 、 T 。出乎意料的是,直线 RX 、 SZ 、 TY 共点于点 Q 。这个复杂的构形展示了如何从一个共点性构建出另一个看起来完全不相关的共点性。
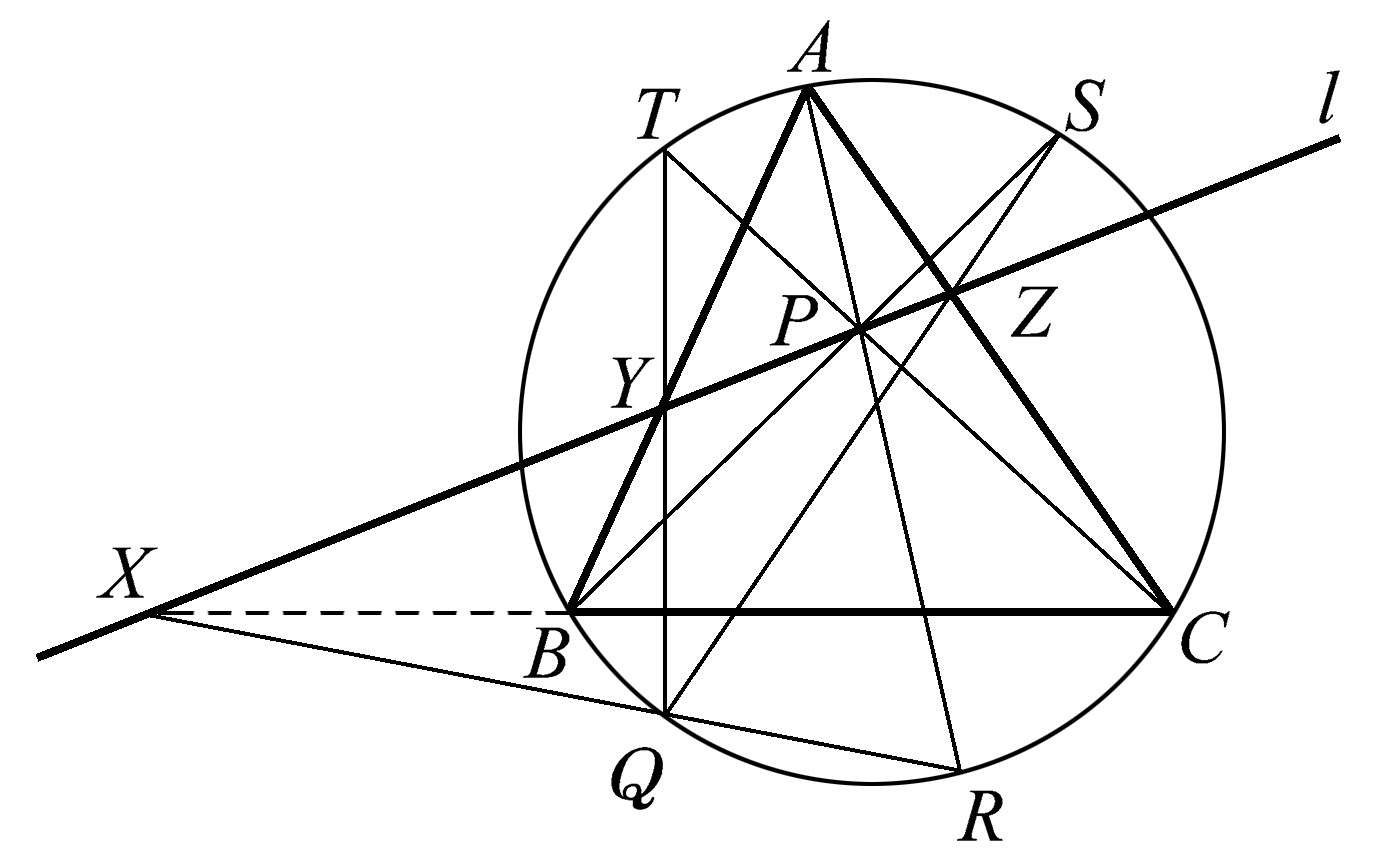
图1.109
现在让我们看一些多边形的共点性。在图1.110中,我们看到一个六边形外接于一个圆。如果这是一个正六边形,那么它的各条对角线肯定是共点的。但是图中的六边形是一个不规则的六边形,唯一的条件是它外接于一个圆,这意味着这个圆与六边形的六条边都相切。出乎意料的是,在这种情况下,我们再次发现六边形的各条对角线共点于点 P 。
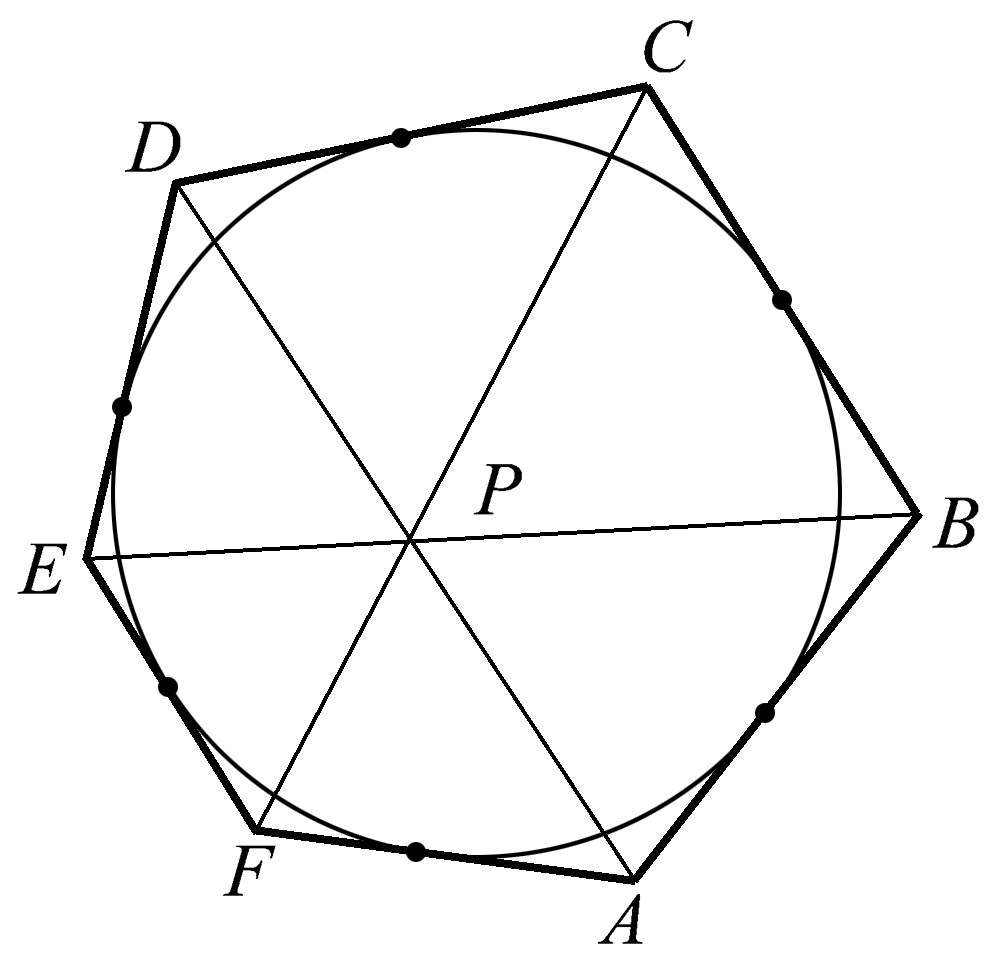
图1.110
1806年,21岁的法国学生布里昂雄(Charles Julian Brianchon,1783—1864)发现了这一不寻常的关系,他后来成为一名数学教授。此外,这一关系不仅适用于圆,也适用于椭圆。也就是说,如果一个六边形外接于一个椭圆,结果也一样:连接相对顶点的各条对角线是共点的,如图1.111所示。
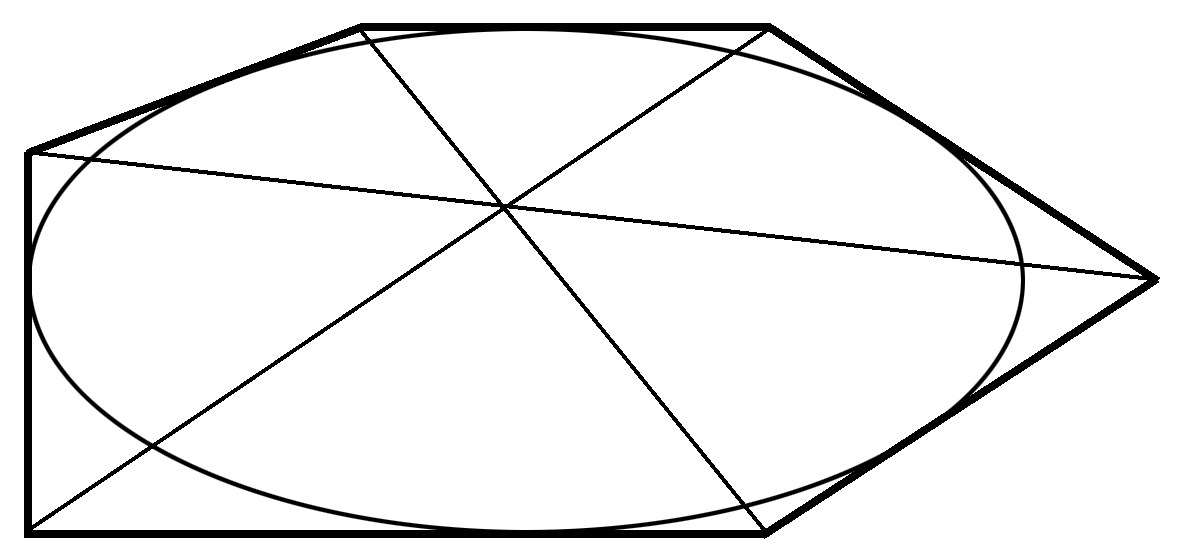
图1.111
既然我们还在讨论多边形,让我们来考虑一个外接于一个圆的不规则五边形,如图1.112所示。图中,两条对角线 AD 和 BE 相交于点 P 。而连接顶点 C 和其对边的切点 F 的直线与上述两条线共点于点 P 。这种情况和六边形的情况有一种非常微妙的关系。我们把它留给志存高远的读者去发现。
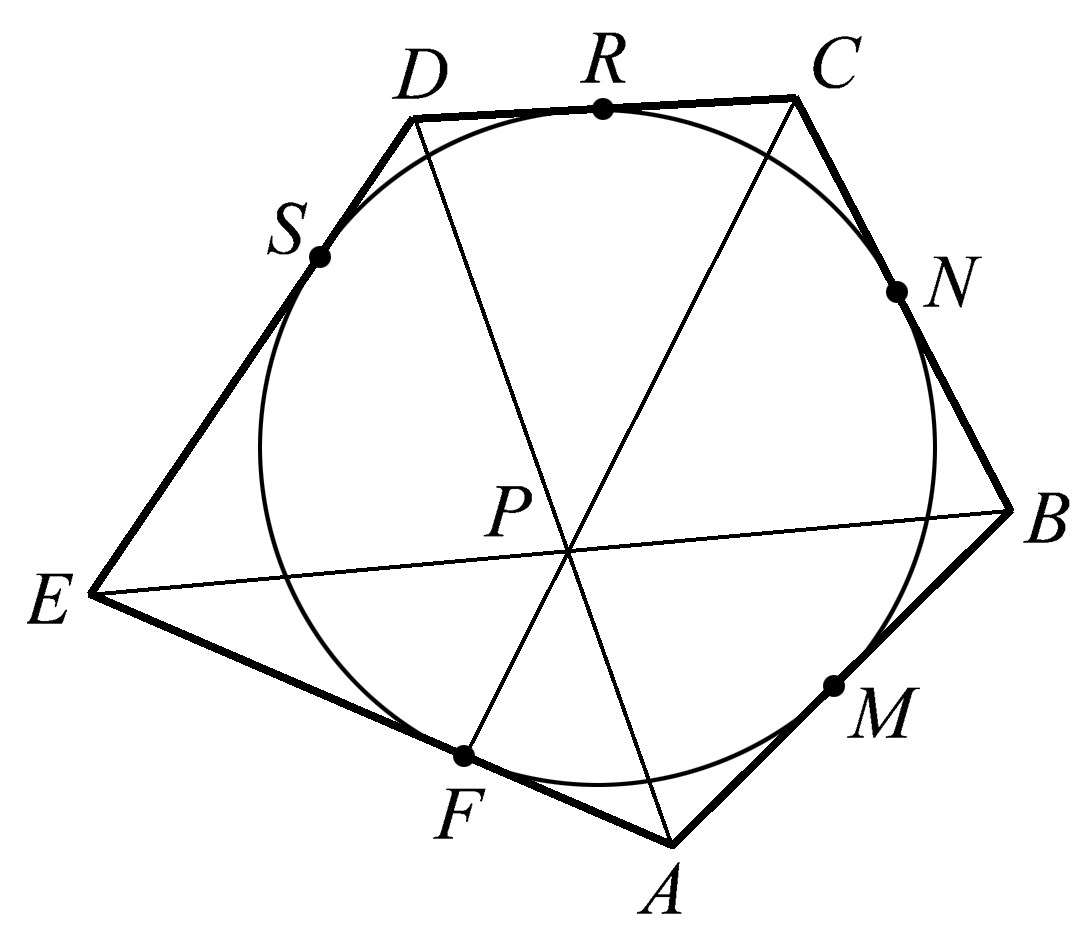
图1.112
在多边形上可以找到更多的共点性。作为一种消遣,也作为对跃跃欲试的读者的一个挑战,我们首先考虑一个正十八边形(即各边相等、各角也相等的多边形),如图1.113所示。接下来的几个图形中出现了许多神奇的共点性供大家欣赏。我们在这里描述其中的一些例子,其他的留待读者去发现。先从图1.113开始,4条线关于对角线 AK 对称,且与 AK 共点于点 P 。
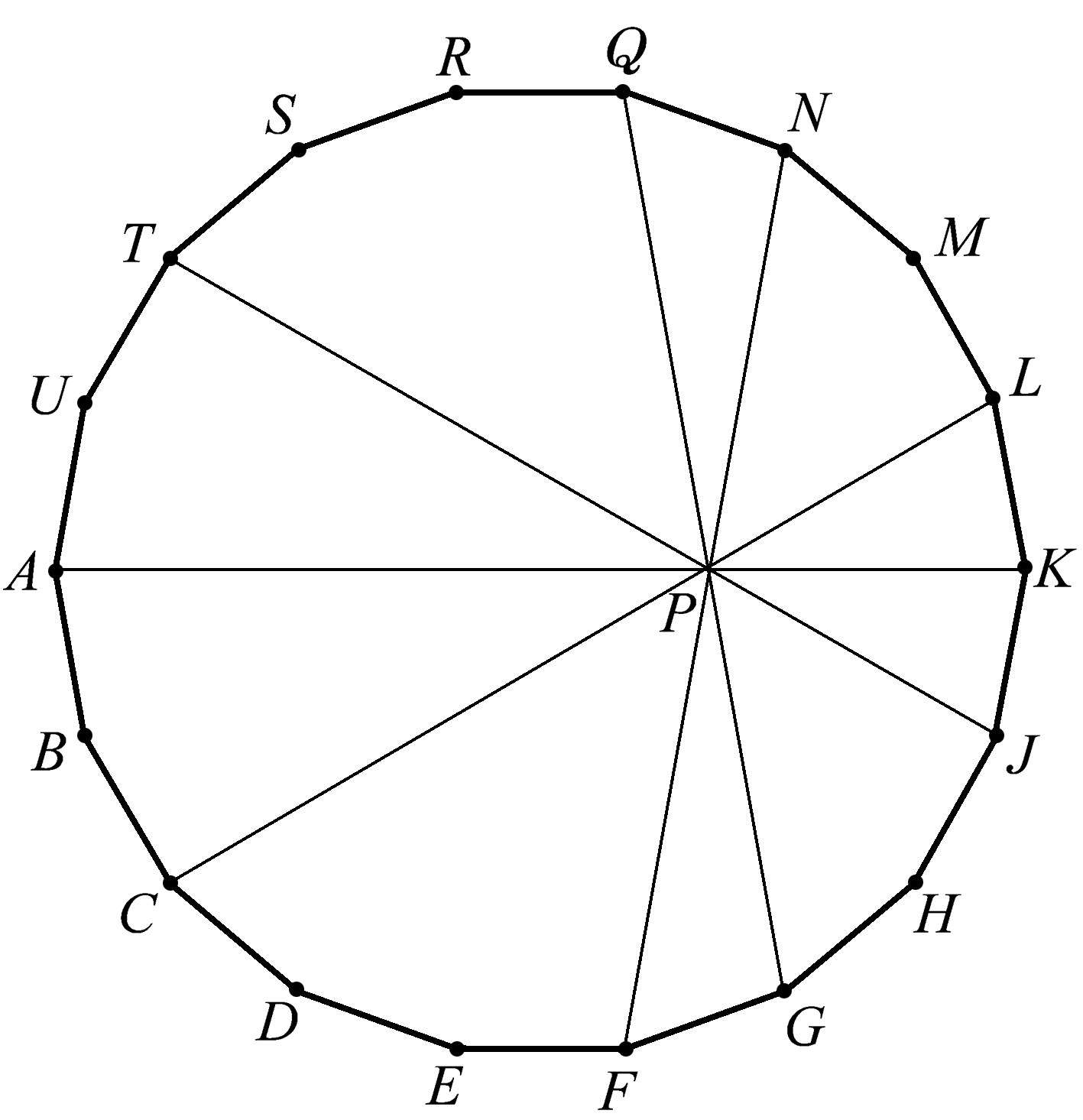
图1.113
在图1.114所示的正十八边形中,也有4条对角线关于中心对角线 AK 对称,且与 AK 共点于点 P 。

图1.114
图1.115到图1.118显示了在正十八边形中的另外几组共点线。
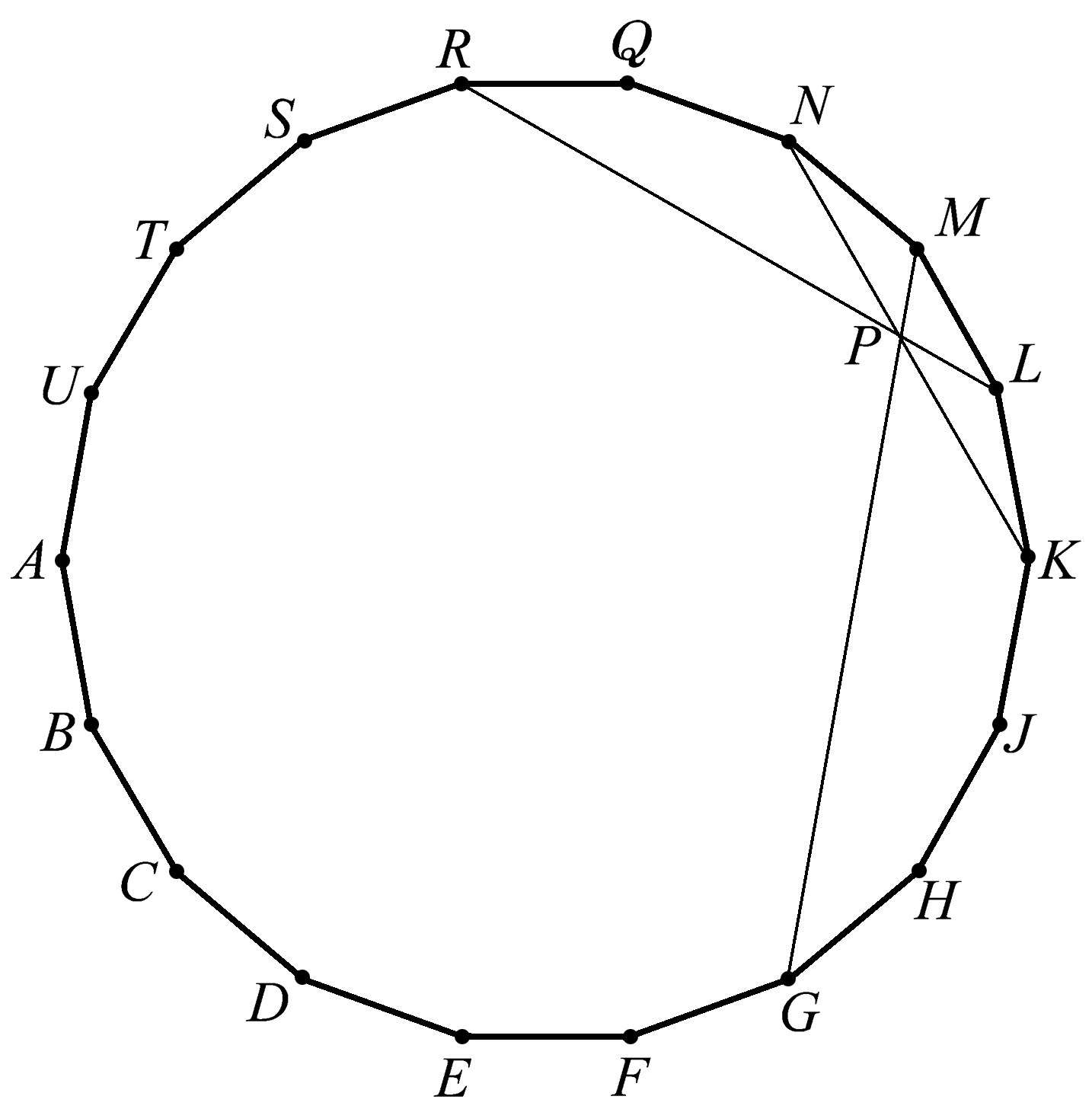
图1.115

图1.116
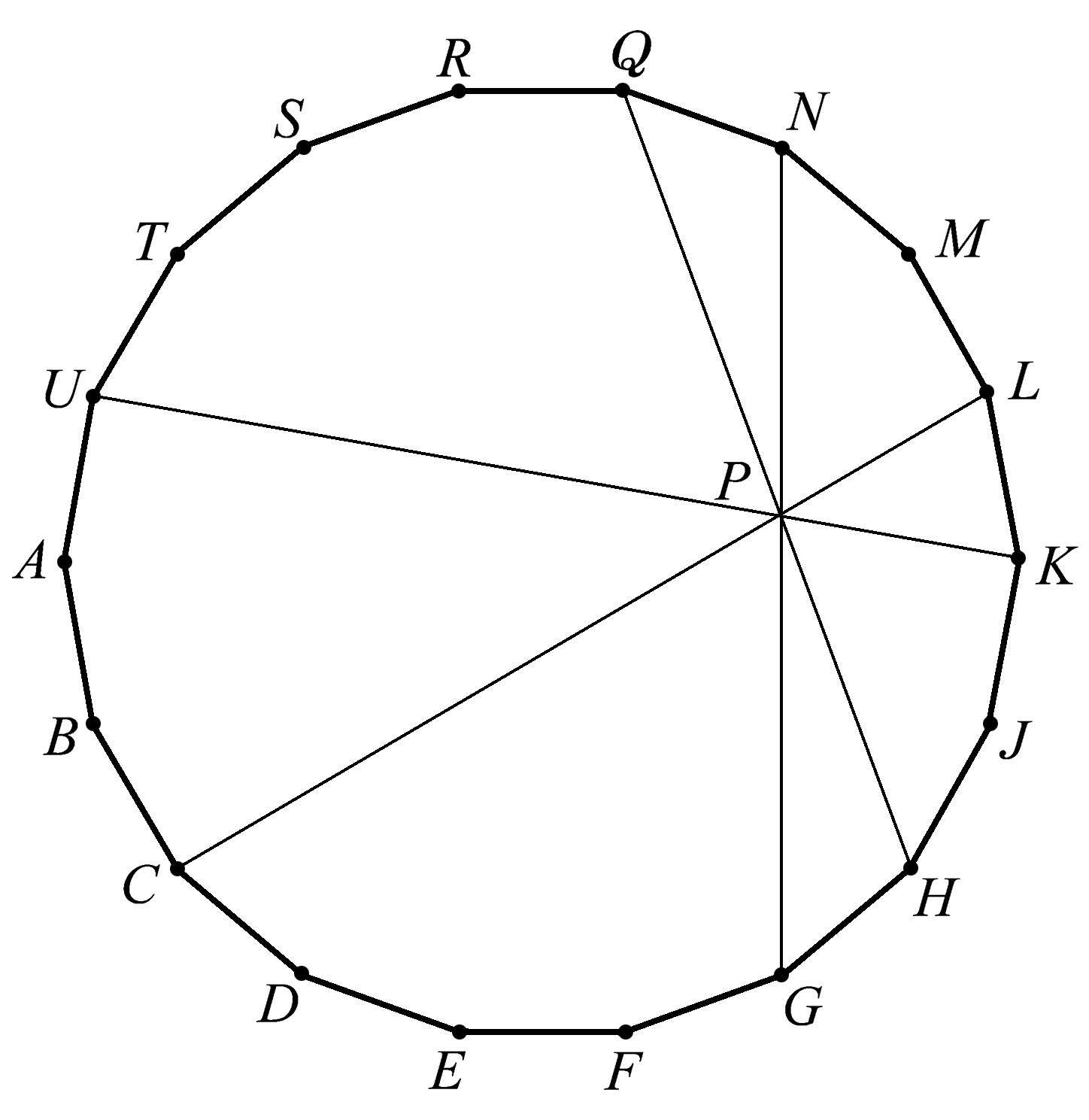
图1.117
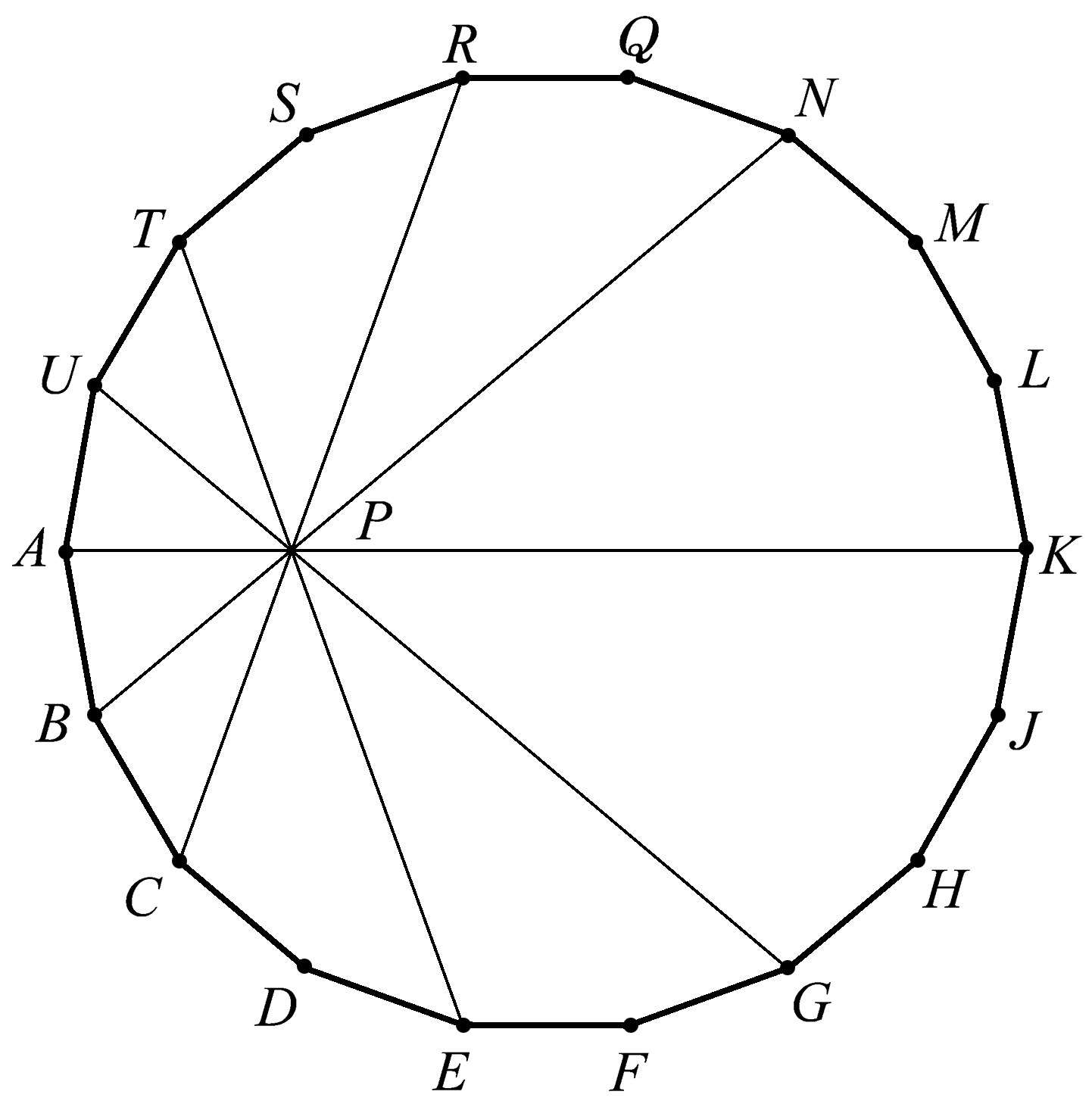
图1.118
在开始探索这些共点性之前,我们再探讨一个例子。在图1.118中,有5条线,它们共点于点 P 。请注意,在这些例子中,线段之间存在某种对称性。
我们现在已经完成了直线共点性的探讨,接下来将讨论类似的内容:三个点或更多点共线,即位于同一条直线上的点。