




虽然人类对有些文化根类别上的超常刺激做出反应,偏爱度却并非单调地随着刺激的一个连续的强化而增加。在所有对我们已知是被检测过了的类别中,存在被偏爱超过其他更极端者的中间值或值域。例如,在关于动机的研究中,这一原理被很好地建立了起来。施罗德(Schroder)与同事们(1967)记录了在中等复杂水平上情感回报与信息处理的最大化。他们建构了一个一般模型,试图预测这些峰值,作为信息内容、回报以及计算困难与情感压力的负面效应的最大总和。
相同的原理在认知研究中被独立地引证了。人们倾向于分解信息为相对少数的类别。正如前面提到,米勒(1956a)提出,该数目就是神话与民间传说的“魔力七”,加或减二。回顾那时的文学,他展示出,在没有特殊训练与辅助而有小错误的情况下,区别纯粹的声调、味道、大小、颜色与温度的能力,事实上是通常被限制在这个范围之内的。最近以来,彭德塞(Pendse)(1978)证明,在通信系统中,类别的最佳数目,一般是一个信号—噪声比的函数。一个信号在一条嘈杂的通道中被传递的次数越大,信号任一采样可被分解而成的类别的最佳数目就越小。如果此数学推导关系在生物进化期间被遵守,那么大脑本身的设计就有可能被预见到相当精确地具体指定普通的、直觉的分类中所采用的复杂程度。这一假说可部分地通过下列由数学模型所生成的预测来检验:左脑半球,其必须用言语表达且因此比右半球更广泛地再传递信息,将会在有着少量类别的处理系统中表现得更好。当类别数被增加,优势将会转向右半球。这一预测被彭德塞的实验研究证实了。
样式区别与偏爱的情感成分,在美学的实验研究中变得至高无上。在关于多边形(正方形对八边形对六角星,以此类推)的研究中,艾森克(Eysenck)(1968)发现,受偏爱的图形具有下列品质:较不熟悉、对称、非直角,以及有许多不平行的边。拉舍夫斯基(Rashevsky)(1960)走得如此之远,以至于设计出一个神经学模型来说明此类数据。他得到一种紧密的匹配,于该假设被做出之时,即,愉快中枢为在重复但不同一的系列中许多多余要素的总激发所最大地刺激。
早期美学实验中用到的多边形,在复杂度上有所限制,结果数据只揭示出在复杂性尺度较低一端美学反应的相关性。斯梅茨(Smets)随后的研究(1973),使用着间接但更能精确测量的阿尔法脑波阻滞反应作为一种唤起的信号,指出当竞争图案被制作得更复杂时,中间最大量的存在(见图3.9)。
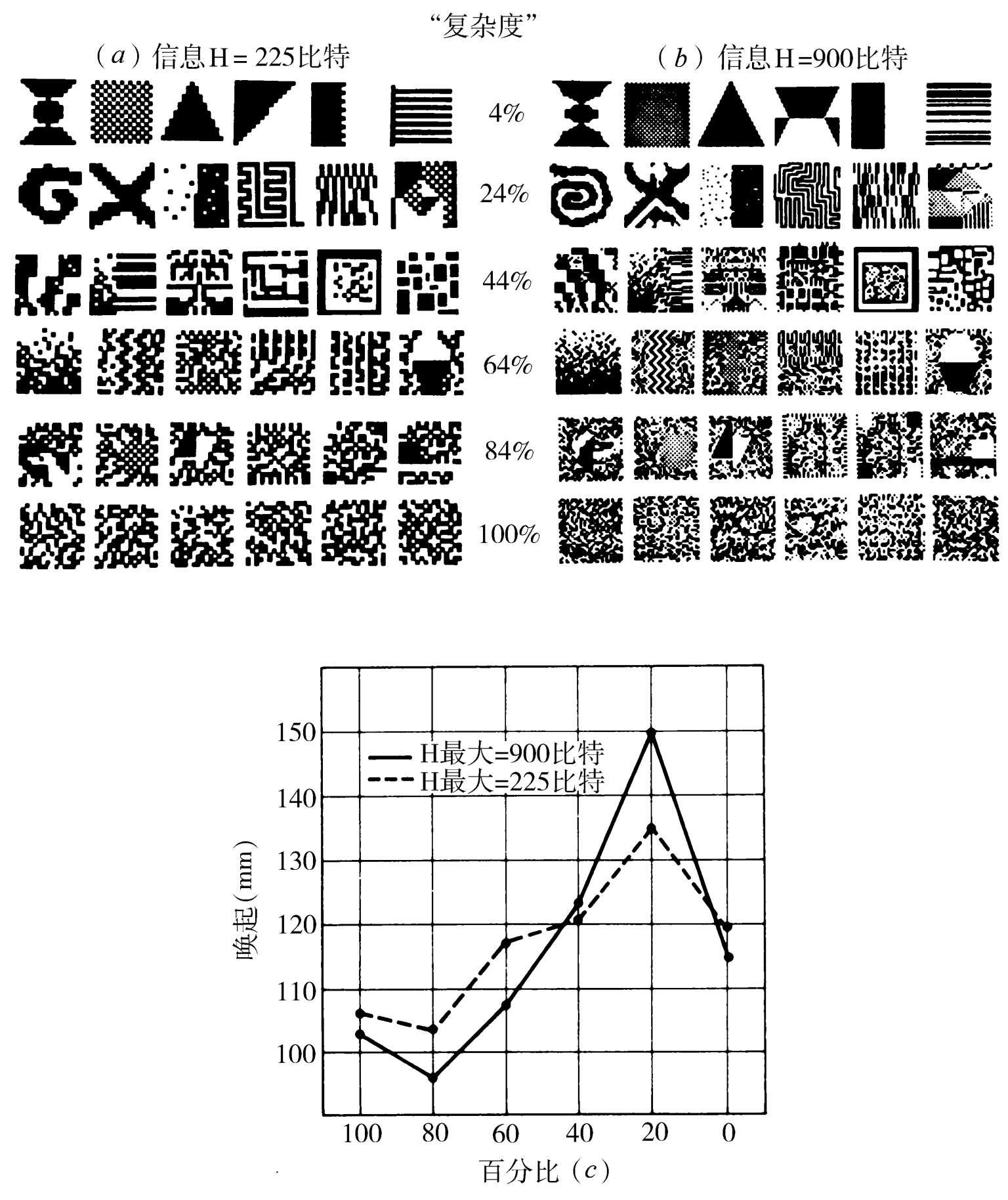
图3.9 视觉样式上达到中等复杂度水平的最大唤起。在这一实例中,复杂度是由元素数目上不同的两个系列中冗余度的百分比来测量的(一个系列生成225比特,另一个是900比特的不确定度)。唤起测量的是跟随图形的出现,脑电图的阿尔法波被阻滞(去同步)的时间;给出的数字是与多导记录仪记录一致的相应距离。下面图表中的各点给出67个人的平均反应。(依照Young,1978;来自Smets,1973)
有趣的是,对中等复杂度图案的偏好,可追溯到最早的婴儿期。赫申孙(Hershenson)与同事们(1965)向新生儿展示一系列随机构造的图形,根据它们是否包含5个、10个或20个拐弯而分类。婴儿们最一致地凝视在有10个拐弯的系列上(见图3.10)。其后,模式挑选更精确的后成规则,牵涉复杂度作为一个关键变量,为范茨及其合作者们的视觉发育实验所揭露(见表3.1)。
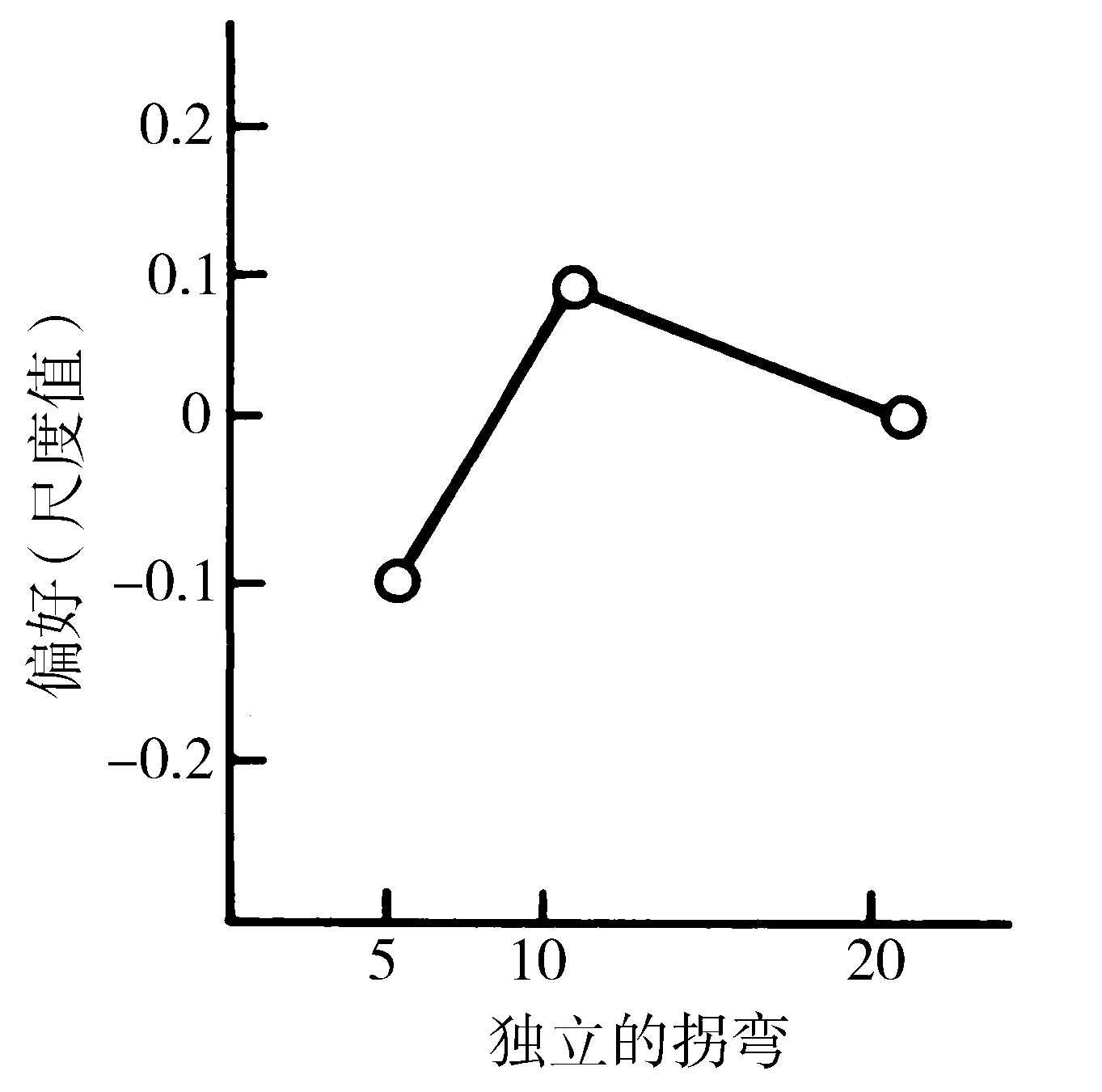
图3.10 复杂度挑选中的一个后成规则。给出的偏好测量被展示随机生成图形系列的新生婴儿眼睛注视的相对时长。图形中的复杂度由沿其边缘的拐弯的数来测量。(修改自Hershensonetal. ,1965)
统治复杂度挑选、问题解决以及美学的发育的后成规则的知识,仍然是粗浅的。伯利内(Berlyne)(1971)与博茨(Bortz)(1978)总结出,在现有知识的基础上,唤起曲线与主观美学判断之间,简单的联系无法被做出。不可能的是,美学判断上的偏好曲线,会是代表着唤起曲线那样的单峰形态。而看起来还是有可能的是,强大的间接联系确实存在,并且使文化进化受到了有意义的影响。进一步说,复杂度的平均最佳水平,以及种群内水平频率分布的更高阶矩,可初步诠释为智人的物种特有特征。当用其他智能动物物种,尤其是旧世界的猴与猿类来进行可比较挑选实验时,它们将被更加清楚地理解。