




1)化工过程的多稳态特征
描述化工过程的动态方程,即状态变量对于时间的常微分方程组,通常具有多个稳态解。稳态解是指动态系统中使得系统变化率为零的操作点。根据稳态点在扰动后是否能够回复到之前稳态操作点的动态特性,可以将稳态操作点划分为稳定的稳态操作点和不稳定的稳态操作点。Seider等强调了化工过程设计中对系统非线性特性分析的重要性。袁其朋等研究了固定化酵母粒子中生产乙醇的定态分岔行为,找到了该过程的多个稳态解。Balakotaiah等用分岔理论分析了在简单全混釜的多稳态特性。Razon等在综述了化工反应系统中的多态及不稳定特性的基础上,在研究中也观察到在简单连续搅拌釜反应器中存在多稳态解和周期振荡现象。Monnigmann等提出了针对强非线性过程提高系统稳定性的优化设计方法,并将该方法用于醋酸乙烯酯聚合过程、甲苯加氢脱烷基化过程以及混合悬浮混合排料(MSMPR)结晶过程。Meel等在研究多目标优化的设计方法中也指出在反应系统中存在多稳态解的现象。Marquardt等提出了非线性动态过程构建方法(CNLD),并将该方法用于色氨酸合成过程。Lemoine-Nava等利用非线性分岔分析方法分别对苯乙烯自由基聚合反应器进行了分析,对控制系统的设计给出指导建议,同时也对聚亚安酯釜式反应器的开环系统进行了研究,讨论了系统的多稳态特性。Katariya等通过分岔分析确定合成甲基叔戊基醚(TAME)的反应精馏过程中存在多稳态,指出进料状态和Damkohler数的变化是产生多稳态的原因。Mancusi等进行了工业合成氨反应器的多稳态研究,揭示了合成氨反应器在一次操作中压力减小造成持续震荡进而引发事故的机理。除了定性地判断化工过程稳态操作点的稳定性之外,还需要对多个稳定的稳态操作点定量描述它们的稳定性。针对这个问题,从稳定的稳态操作点遇到扰动后的动态响应特性来定量描述:稳定的稳态操作点能够承受的最大扰动范围,稳定的稳态点在扰动后回复到之前操作点的速率。
2)稳态操作点的稳定性表征
通常情况下,对于化工过程中稳定的稳态操作点,在遇到小的扰动之后,随着时间的推移能够回复到扰动之前的稳态操作点。但是,随着扰动逐渐增大,当增大到某一个特定值后,稳定的稳态点就无法再回复到扰动之前的稳态操作点。因此,研究化工过程稳定的稳态解能够承受的扰动范围,提出抗扰动能力指数,定量表征稳定的稳态解对于扰动的承受能力,可以为进一步设计本质安全化的化工过程提供依据。
除了能够承受的最大扰动范围不同外,稳定的稳态点在遇到扰动后,回复到扰动之前的稳态点的速率也不相同。即使距离很近的两个稳定的稳态操作点,在扰动下的回复速率差别也很大,即回复到扰动之前的稳态操作点所需要的时间差别很大。因此,在化工过程设计中,优先考虑扰动后回复速率较快的操作点作为设计方案中选择的操作点。
在化工过程设计中,为了精确地比较不同稳定的稳态点的稳定性,需要量化表征稳定的稳态操点在上述两方面的特性。对于已有的多个稳定的稳态操作点,量化表征后的稳定性指数可以为多目标优化设计提供基础。
对于化工过程的动态系统方程:
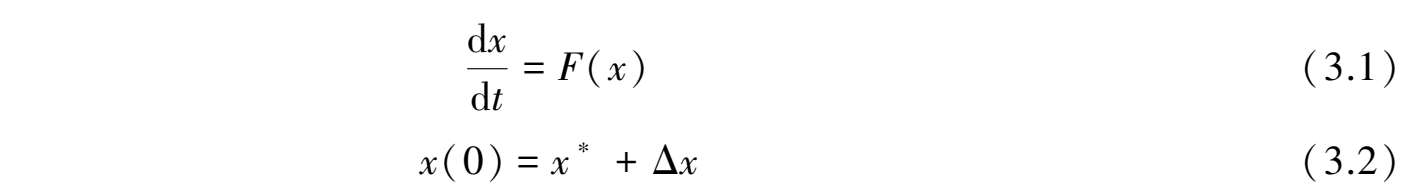
式中 x * ——系统稳定的稳态解;
Δ x ——系统遇到的扰动。
稳定稳态点所能承受的最大扰动范围( RI )的量化表征的一种构造方法为:
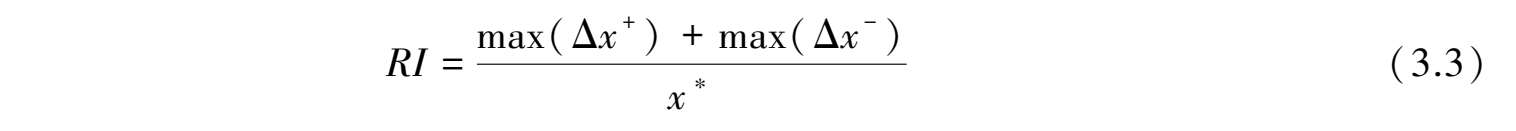
式中 Δ x + ≤ x * ,Δ x -≤ x * ,Δ x + 和Δ x - ——分别是系统所能够承受的正向扰动和系统所能够承受的负向扰动。
用 SI 表示稳定稳态点在扰动后回复原来操作点速率的大小,一种构造 SI 的表达式如下:
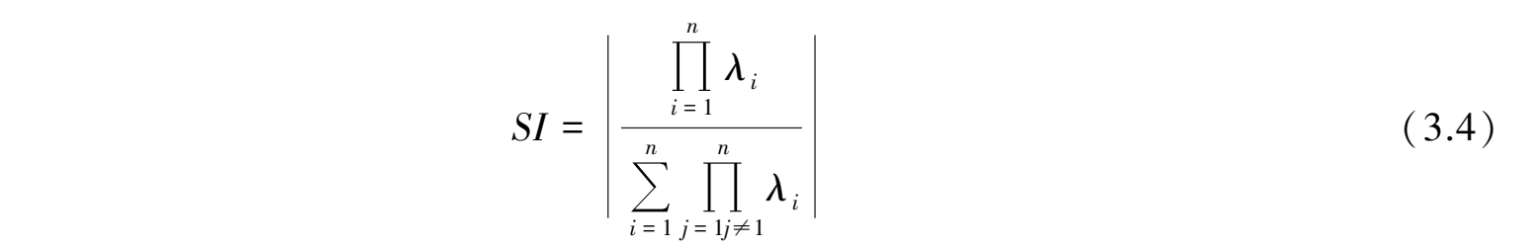
式中 λ i ——动态方程组雅可比矩阵在稳定的稳态操作点处的特征值。
将 RI 和 SI 归一化,定义稳定性指标为 QI ,构造 QI 的表达式如下:
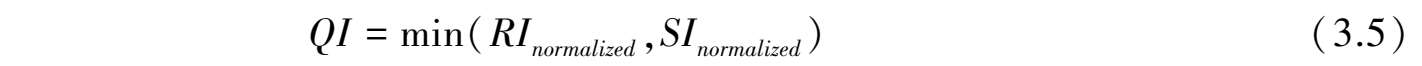
通过设计的 QI ,可以量化表征不同稳定的稳态点的稳定性,从而为多目标优化提供依据。
综合考虑经济性和稳定性两方面的因素,需要进行多目标优化设计。确定化工过程动态系统中稳定的稳态点的稳定性的表征方法之后,相应的优化设计具体步骤如下:
①求解动态系统的所有稳态解。
②判断系统稳态解的稳定性,划分出稳定稳态解区域和非稳定稳态解区域。
③对于稳定的稳态解区域内的操作点,计算 RI , RI 越大,能够承受的扰动范围越大。
④对于稳定的稳态解区域内的操作点,计算 SI , SI 越大,遇到扰动后收敛速率越大。
⑤将 RI 和 SI 归一化,计算稳定稳态解对应的 QI 。
⑥基于 QI 建立多目标优化方程,求解计算优化方案。
在化工过程设计中,通过对操作点稳定性的量化表征,在化工过程设计阶段充分考虑系统的稳定性,选择能够承受较大范围扰动,同时在遇到扰动之后能够迅速回复的稳定的操作点作为优化设计方案。
化工过程中存在复杂的非线性动态特性,除了多稳态现象之外,在特定的操作条件下系统还会自发产生持续的振荡现象,振荡现象在连续发酵过程中报道较多。
微生物发酵过程是复杂的生化反应过程,常产生多稳态、自发持续振荡等现象。应用数学方法对此类问题建模并分析其解的渐近性态,探讨发酵过程的优化控制等问题一直都是人们关注的研究方向。从文献统计来看,关注较多的是以微生物连续发酵生产1,3-丙二醇体系和运动发酵单胞菌连续发酵生产乙醇的体系中的振荡现象。
1)肺炎克雷伯菌连续发酵生产1,3-丙二醇
1,3-丙二醇(1,3-PD)是一种重要的化工原料,是合成许多具有优良特性的聚合物的单体。相对于化学合成法,微生物发酵生产1,3-丙二醇具有原料可再生、操作简便、反应条件温和、副产物较少和环境污染小等优点。1,3-丙二醇发酵体系中存在Hopf奇异点,在奇异点附近会产生周期性的振荡,对应为极限环,如图3.1所示。
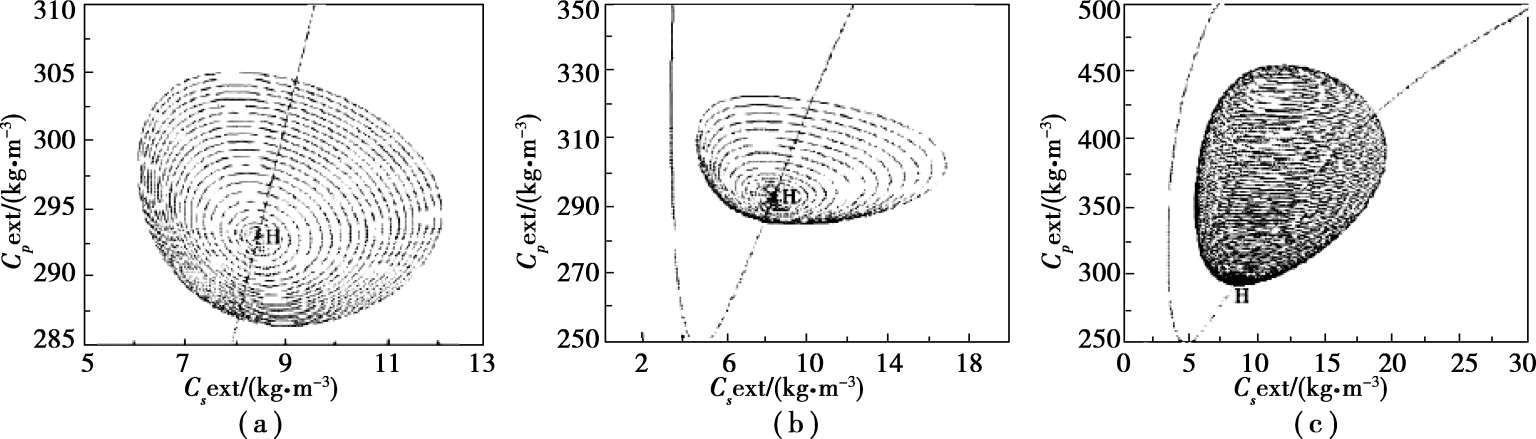
图3.1 Hopf奇异点附近引发的极限环(a)Limit cycles(part Ⅰ);(b)Limit cycles(partⅡ);(c)Limit cycles
在该体系中,随着操作条件的变化,Hopf奇异点的位置也发生改变,在由两个主要操作参数组成的操作平面内,Hopf奇异点的分布如图3.2所示。
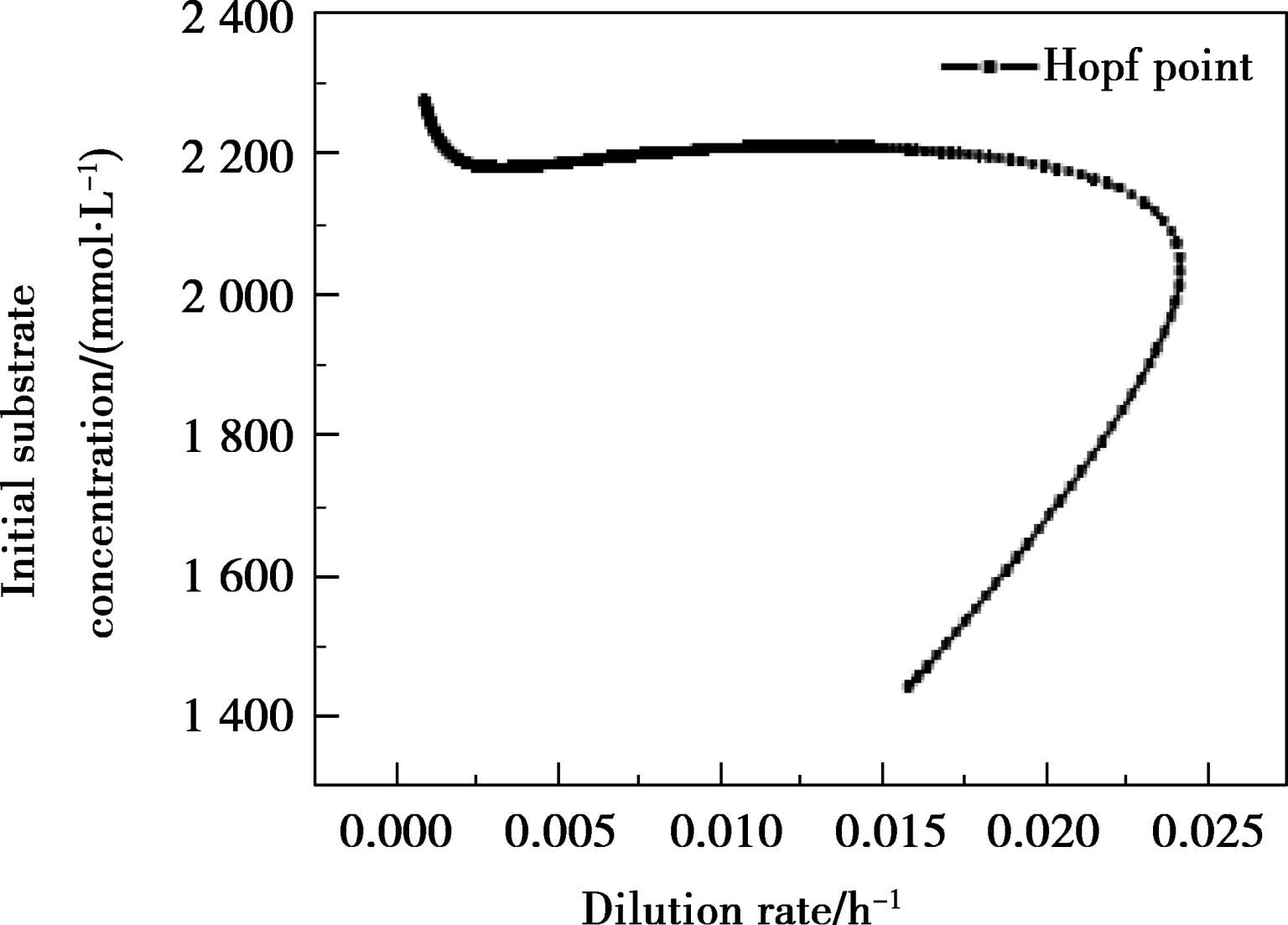
图3.2 操作参数域上的Hopf奇异点
对于操作参数域上的奇异点,在优化设计过程中,需要考虑操作点与奇异点的距离,这里定义如下的指标来定量描述操作参数距离奇异点区域的距离。
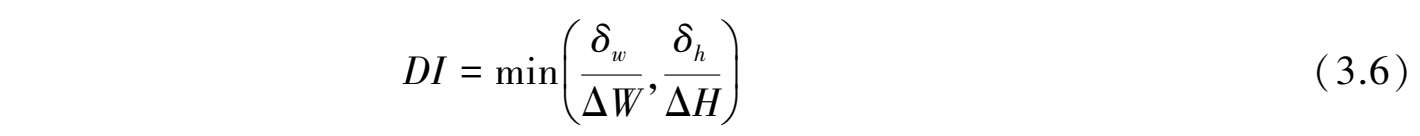
其中,Δ W 和Δ H 分别表示奇异点区域的宽度和高度; δ w和 δ h分别表示操作点距离奇异点曲线的水平距离与竖直距离,因此, DI 描述了操作点距离奇异点曲线的相对最小距离,具体内容如图3.3所示。使用量化表征的操作点与奇异点区域的距离,优化计算最佳的操作参数。当阈值为0.5 时,即允许的 DI 最小为0.5 时,优化结果如图3.4所示。
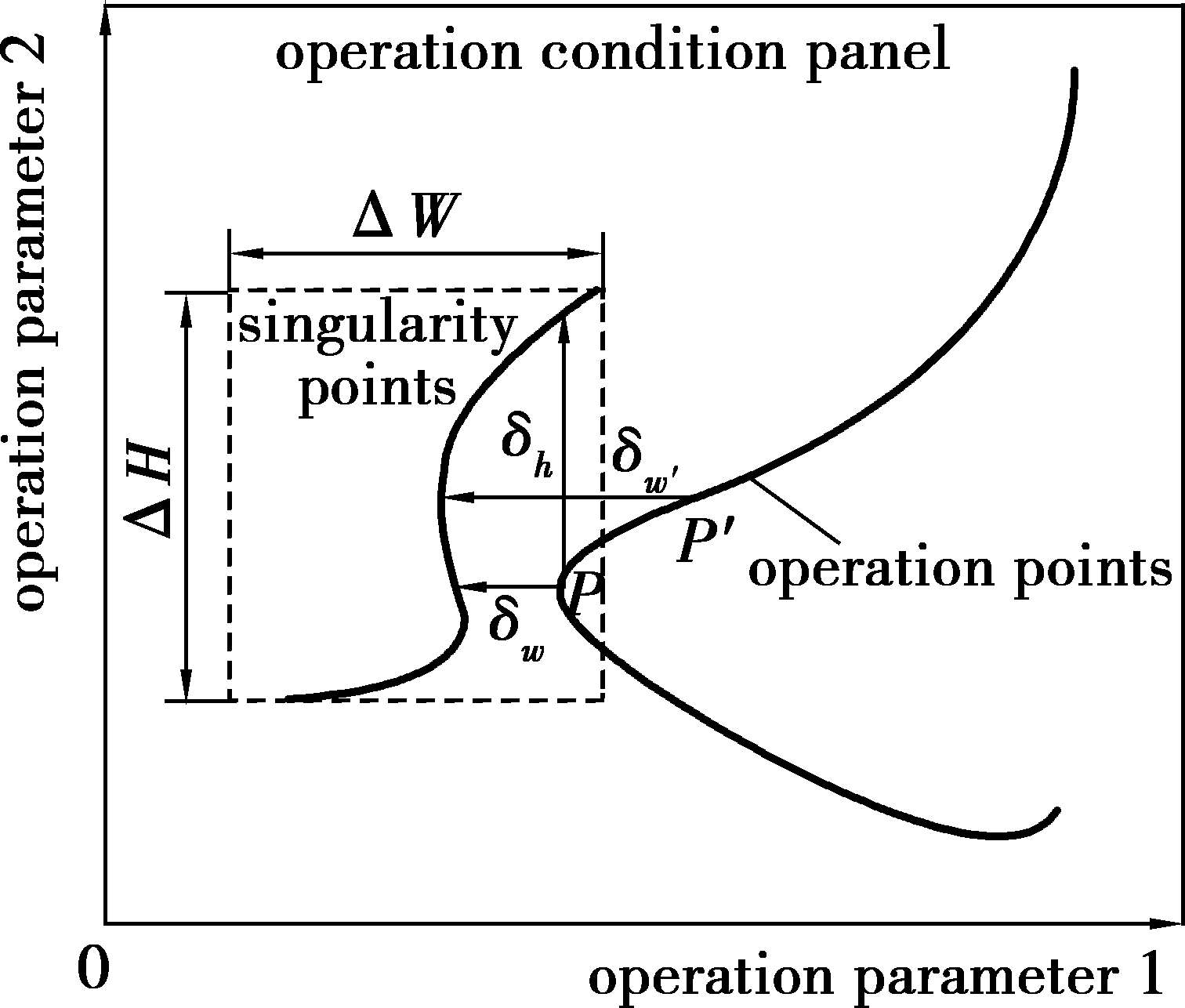
图3.3 定量描述操作参数与奇异点区域的指标
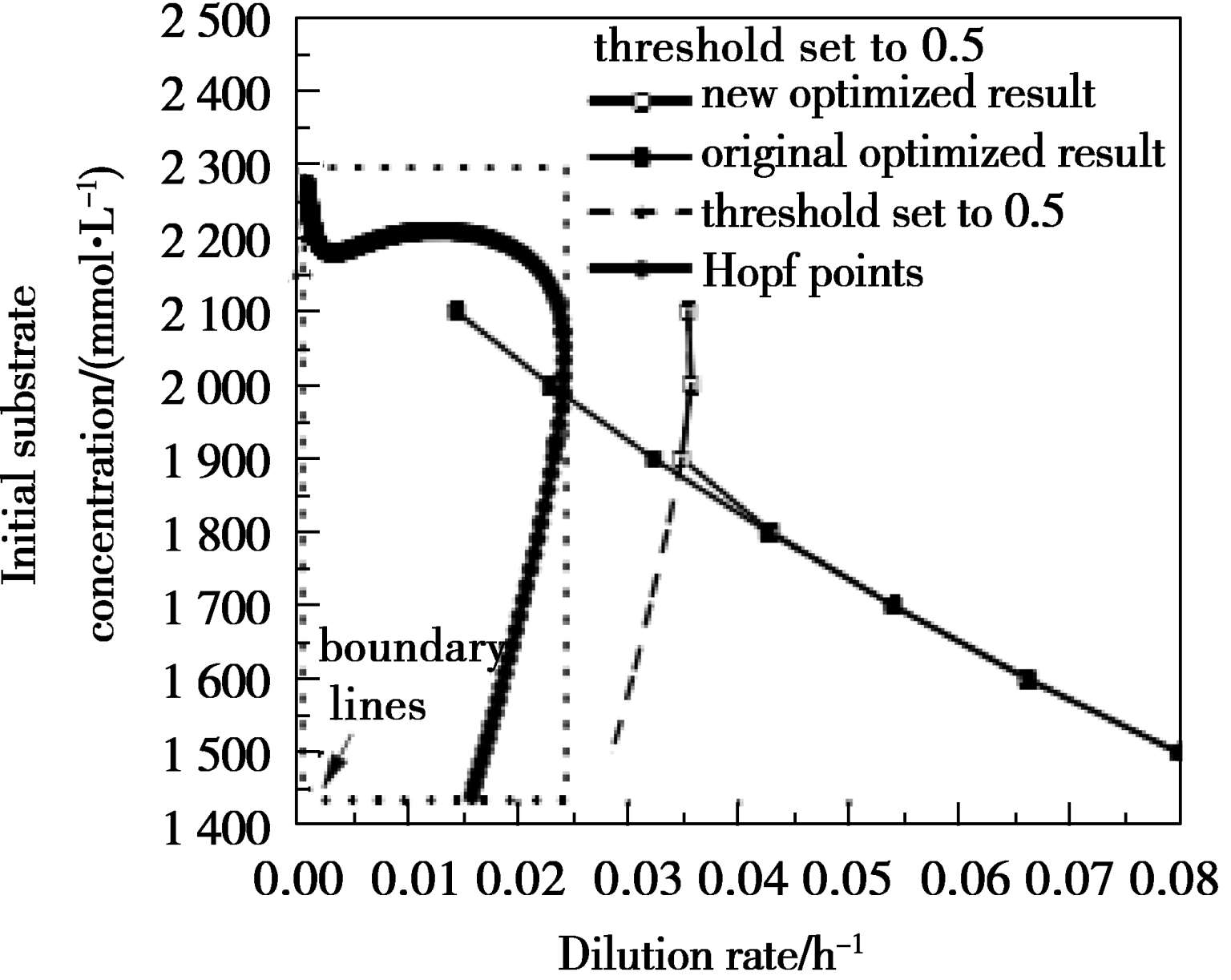
图3.4 DI ≥0.5 时的优化结果
从图3.4 的结果中可以看到,在考虑奇异点区域的约束之后,优化结果可以有效避开可能引发振荡的奇异点区域。通过在设计阶段考虑体系中可能存在的振荡现象,有效避免在这些区域内选择操作点,对于提高体系的稳定性,提高产品的质量具有重要意义。
2)运动发酵单胞菌连续生产乙醇
除了生产1,3-丙二醇的体系外,运动发酵单胞菌连续生产乙醇体系中的振荡现象也是研究较多的对象。
运动发酵单胞菌连续发酵生产生物乙醇。有文献报道,与稳态操作相比,振荡行为难以预测和控制,影响产物收率,因此,需要加以回避或使之弱化。运动发酵单胞菌发酵过程中存在奇异点,在奇异点附近产生的极限环如图3.5所示。周期性变化的振荡现象对于操作过程的平稳以及产品质量的提高都不利,因此,需要在设计阶段采取适当措施规避振荡现象。
在单个操作参数与产物浓度组成的平面上,随着参数的改变,体系中的Hopf奇异点位置发生相应改变,具体如图3.6所示。
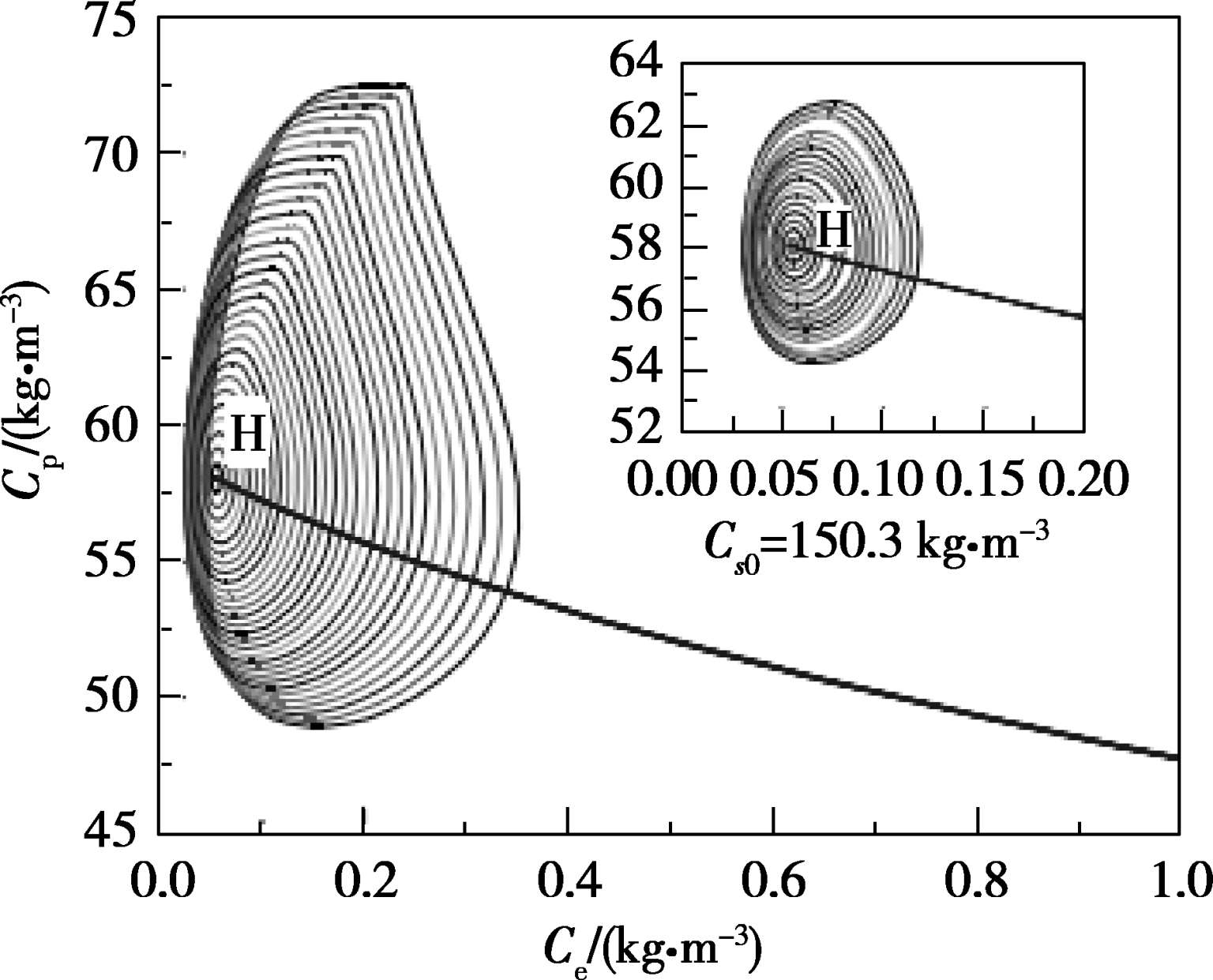
图3.5 奇异点附近产生的极限环
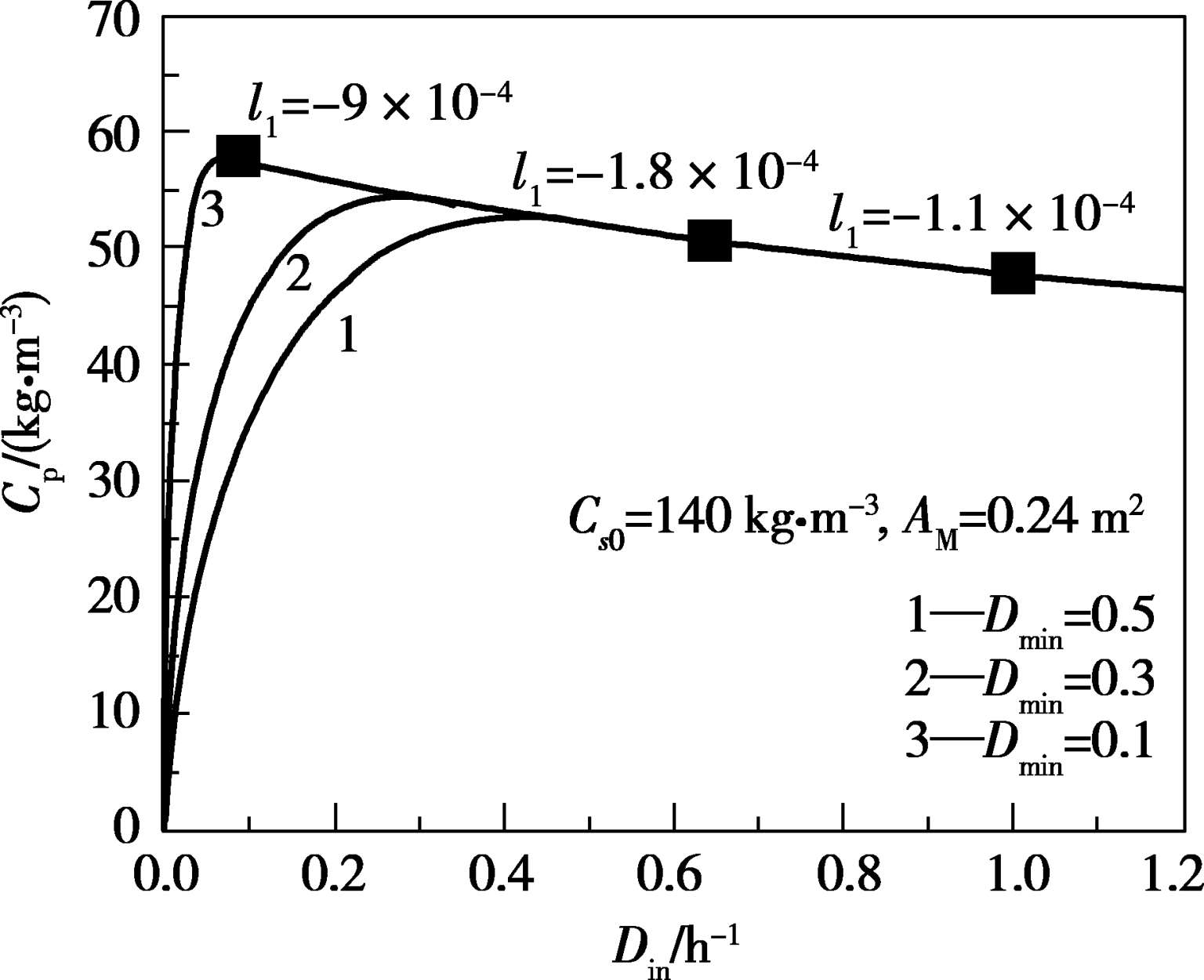
图3.6 不同操作参数情况下体系中的Hopf奇异点
由两个操作参数组成的操作参数域上,体系的Hopf奇异点的分布如图3.7所示。由图可知,在大范围的操作参数域内,都存在奇异点。为了避免从操作点引发的振荡现象,需要与奇异点区域保持一定的距离。此时,对操作点进行优化,得到的结果如图3.8所示。
化工过程的本质安全化设计是一个复杂的工程问题。将操作点的稳定性作为化工过程本质安全化设计的一个重要考虑因素,量化表征稳定的稳态点的稳定性,通过多目标优化,最后找到能够承受较大扰动范围,同时遇到扰动能够快速回复的化工过程操作点。特别针对可能存在的振荡现象,提出相应的奇异操作点的规避方法。通过对两个连续发酵过程的研究,表明了这种方法对于规避可能产生振荡现象的操作点的有效性。
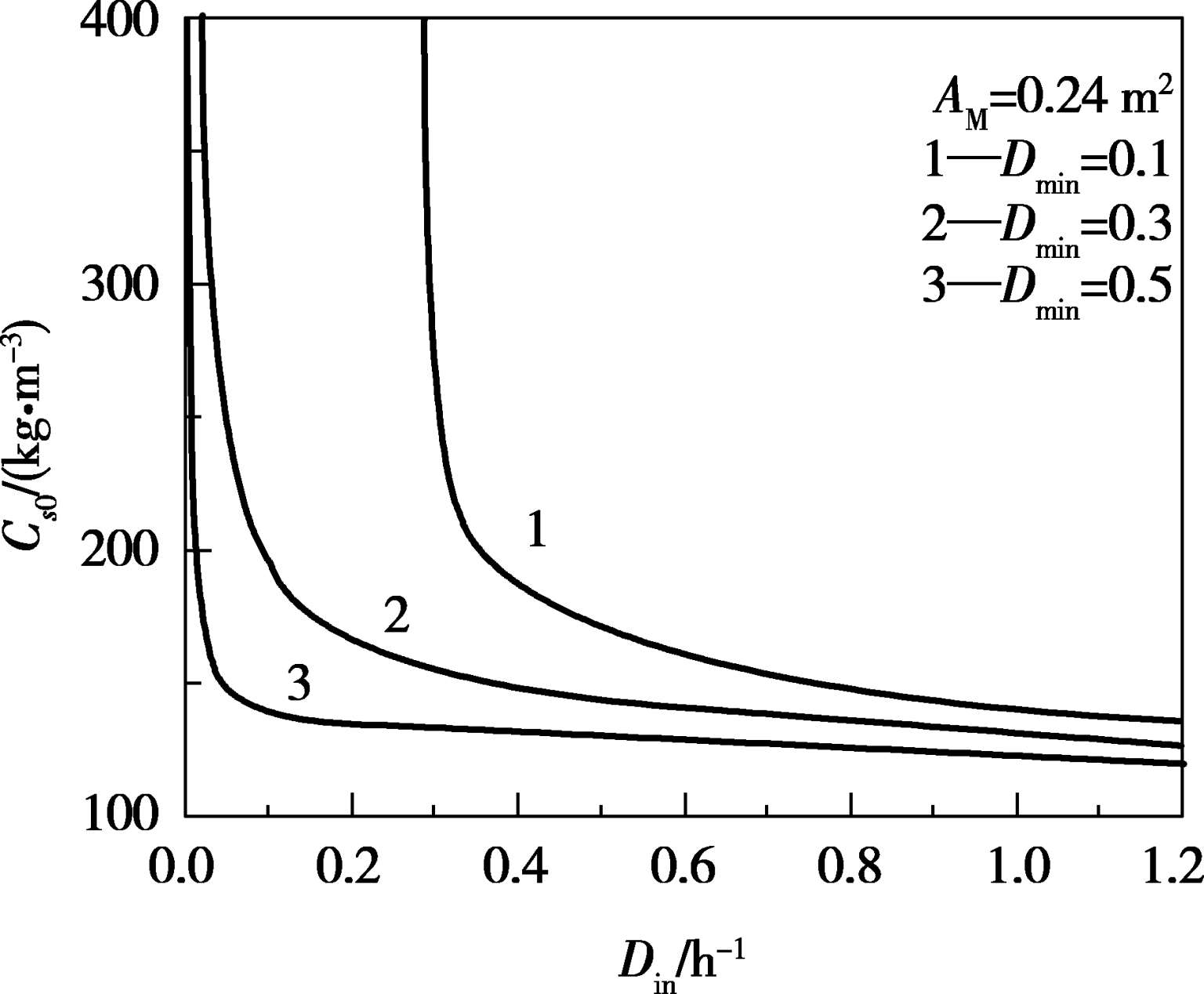
图3.7 操作参数域内的奇异点组成的曲线
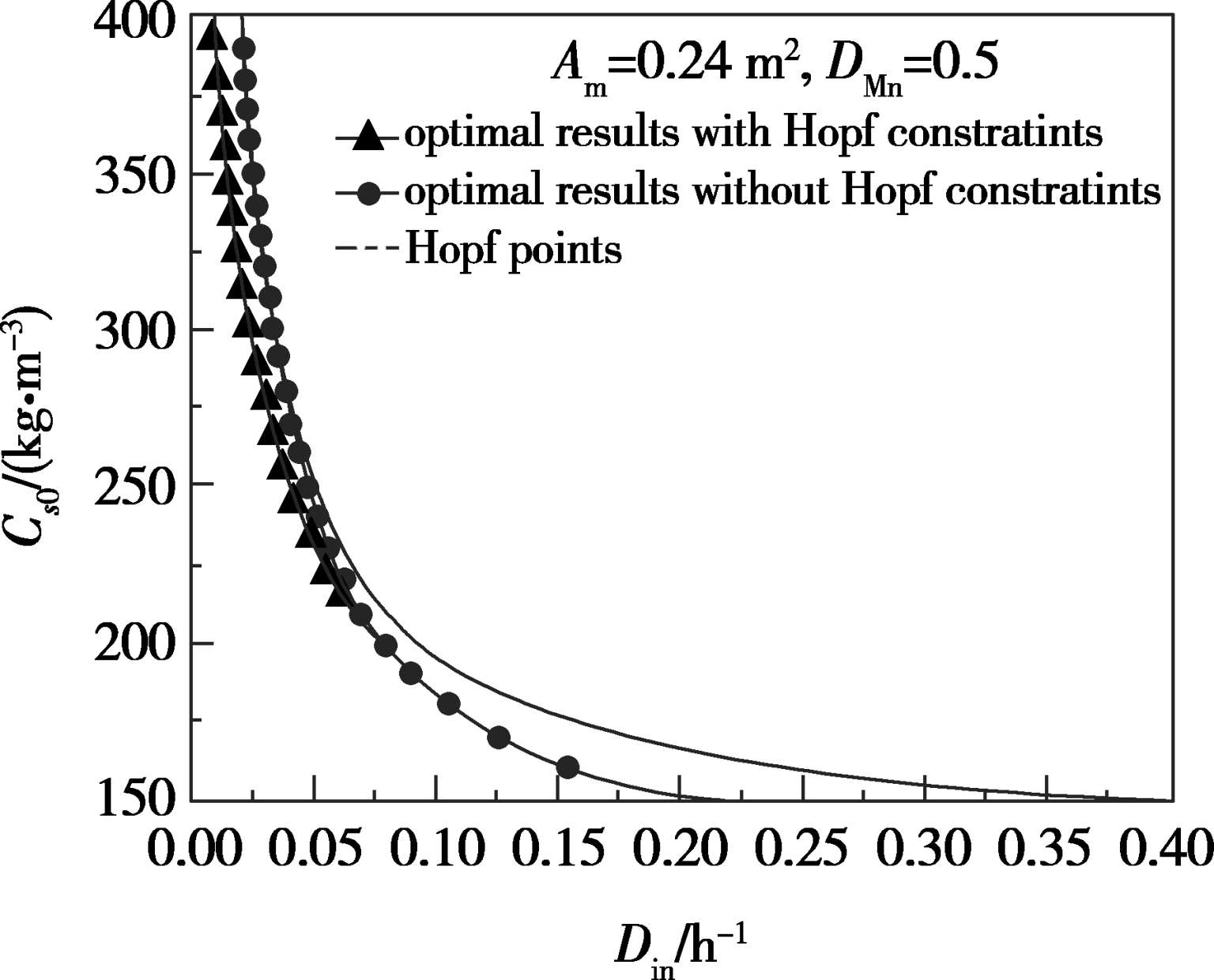
图3.8 优化计算结果
综上所述,通过使用本质安全化的化工过程设计方法,可以设计出本质上具有在不确定因素扰动下仍能维持稳定运行特性的化工过程,进而从源头上降低生产中事故发生的概率,提高化工过程的安全性。