




土方工程的施工,首先必须计算土方工程量。对于场地平整施工,挖填土方量计算出来后,需进行土方平衡调配,然后选择土方施工机械,拟定施工方案,组织土方工程施工。
场地平整施工,一般应安排在基坑(槽)、管沟开挖以前进行。这样,能使大型土方机械有较大的工作面,以充分发挥其工作效能,也可以减少与其他工作的相互干扰。
在场地平整之前,应首先确定场地平整设计标高,然后计算挖方和填方的土方工程量。
(一)场地设计标高的确定
对于较大面积的场地平整(如工业厂房和住宅区场地、车站、机场、运动场等),正确地选择设计标高是十分重要的。选择场地设计标高时,应尽可能满足下列要求:
(1)场地以内的挖方和填方应达到相互平衡,以降低土方运输费用;
(2)尽量利用地形(不考虑泄水坡度时),以减少挖方数量;
(3)符合生产工艺和运输的要求;
(4)考虑最高洪水位的影响。
确定场地设计标高的方法,有“挖填土方量平衡法”和“最佳设计平面法”。后者是采用最小二乘法原理,计算出最佳设计平面。所谓最佳设计平面,是指场地各方格角点的挖、填高度的平方和为最小,按照这样的设计平面,既能满足土方工程量为最小,也能保证挖填土方量相等,但是此法的计算较为繁琐。
挖填土方量平衡法,概念直观,计算简便,精度能满足工程要求。
采用挖填土方量平衡法确定场地设计标高,计算步骤和方法如下:
1.初步计算场地设计标高
如图1-2-1 ( a )所示,将地形图上场地的范围划分为若干方格。每个方格的角点标高,可根据地形图上该角点相邻两等高线的标高,用插入法求得。在无地形图的情况下,可在地面用木桩打好方格网,然后用仪器直接测出各角点标高。
从工程经济效益的角度来说,合理的设计标高,应该使得场地内的土方,在场地平整前和平整后相等而达到挖方和填方的平衡(图1-2-1 b )。即:
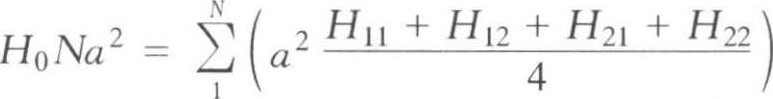
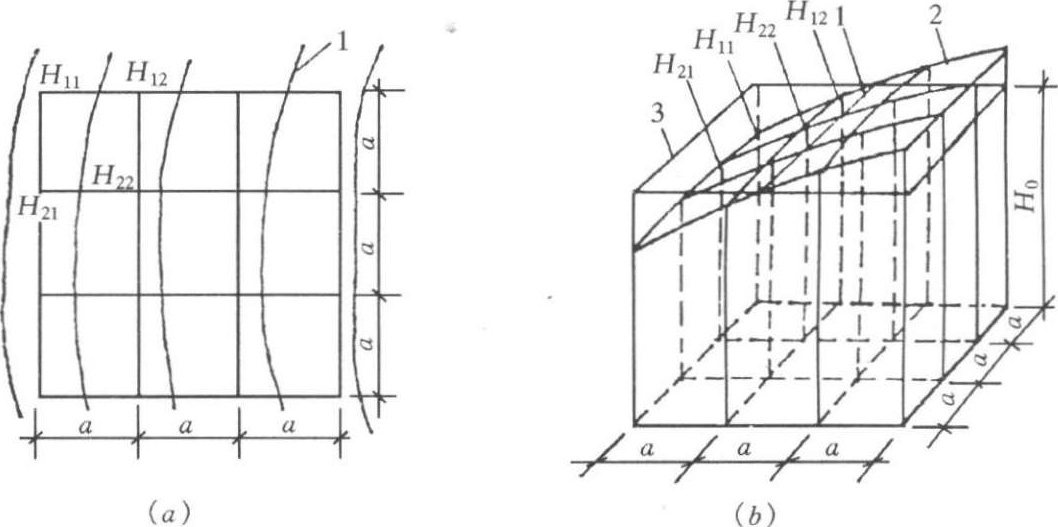
图1-2-1 场地设计标高计算简图
( a )地形图上划分方格;( b )设计标高示意图
1—等高线;2—自然地面;3—设计标高平面;
4—自然地面与设计标高平面的交线(零线)
所以
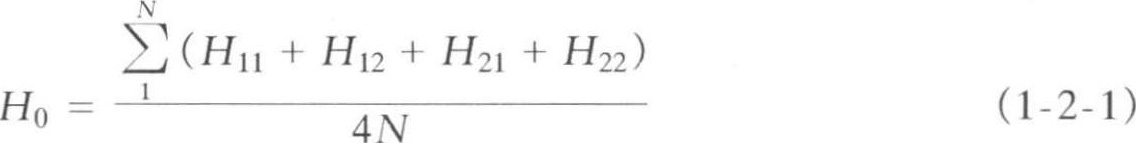
式中 H 0 ——所求的场地设计标高(m);
a ——方格边长(m);
N ——方格数;
H 11 、……、 H 22 ——任一方格四个角点的标高。
从图1-2-1 ( b )中可看出, H 11 是一个方格所具有的角点标高, H 12 和 H 21 均是两个方格共同具有的角点标高,而 H 22 则是四个方格共同具有的角点标高。如果将所有方格的四个角点标高相加,那么,类似 H 11 这样的角点标高加1次,类似 H 12 和 H 21 的标高要加2次,而类似 H 22 的标高要加4次。因此,上式可改写成如下的形式:
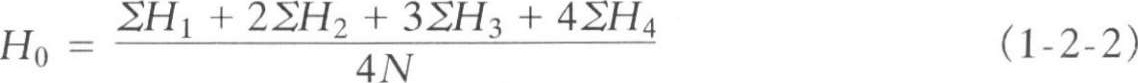
式中 H 1 ——一个方格所有的角点标高(m);
H 2 ——二个方格共有的角点标高(m);
H 3 ——三个方格共有的角点标高(m);
H 4 ——四个方格共有的角点标高(m)。
2.计算设计标高的调整值
式(1-2-1)所计算的设计标高,是一纯理论数值,实际上,还需考虑以下因素调整 H 0 值。
(1)由于土具有可松性,需相应地提高 H 0 值。其提高值可用下式计算:

式中Δ H 0 ——考虑土的可松性而提高的场地设计标高值(m);
V w ——设计标高调整前的总挖方量(m 3 );
F T ——设计标高调整前的填方区总面积(m 2 );
F w ——设计标高调整前的挖方区总面积(m 2 );
K ' s ——土的最后可松性系数。
(2)由于设计标高以上各种填方工程需要用土量而影响设计标高的降低,或者由于设计标高以下各种挖方工程的挖土量而影响设计标高的提高。
(3)由于边坡挖填土方量不等(特别是地形变化大时)而影响设计标高的增减。
(4)根据经济比较结果,而将部分挖方就近弃土于场地之外,或将部分填方就近取土于场地之外而引起挖填土方量的变化需增减设计标高。
3.考虑泄水坡度而计算设计标高的施工值
如果按照式(1-2-2)计算出的设计标高进行场地平整,那么,整个场地表面将处于同一个水平面,但实际上由于泄水要求,场地表面都需作成一定的泄水坡度。因此,还需按照场地泄水坡度的要求(单向泄水或双向泄水),计算出场地内各方格角点设计标高的实际施工值。
(1)单向泄水时各角点设计标高的求法
以采用式(1-2-3)计算出的 H ' 0 并考虑相应因素作调整后的场地设计标高值 H ' 0 ,作为场地中心线的标高(图1-2-2),则场地内任一点的设计标高为:

式中 H 0 ——场地内任意一点的设计标高(m);
H ' 0 ——计算设计标高调整值(m);
i ——场地泄水坡度(不小于 2‰);
l ——该点至 H ' 0 的水平距离;
±——该点比 H ' 0 高取“+ ”号,反之取“-”号。
例如欲求 H 52 角点的设计标高,则:
H 52 = H ' 0 - il = H ' 0 -1.5 ai
(2)双向泄水时各角点设计标高的求法
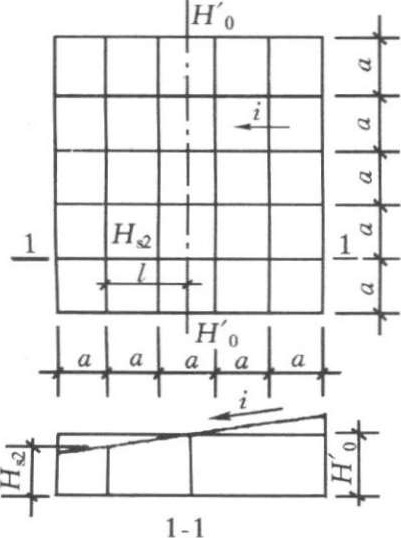
图1-2-2 单向泄水坡度的场地
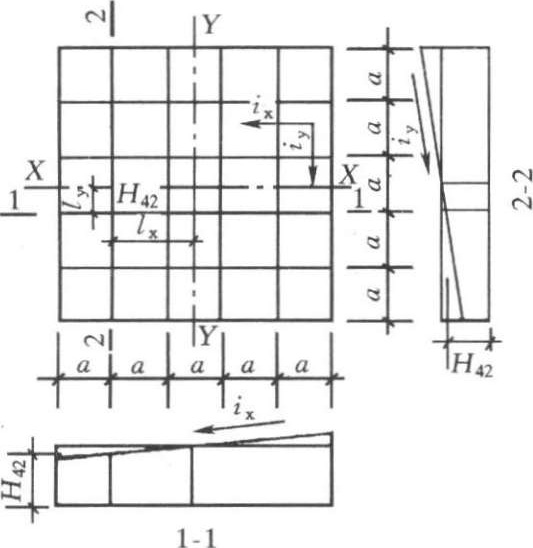
图1-2-3 双向泄水坡度的场地
其原理与前相同。如图1-2-3所示, H ' 0 为场地中心点标高,场地内任意一点的设计标高为:

式中 l x 、 l y ——该点于 x - x 、 y - y 方向距场地中心线的水平距离;
i x 、 i y ——该点于 x - x 、 y - y 方向的泄水坡度。
其余符号所表示的内容同前。
例如欲求 H 42 角点的设计标高,则
H 42 = H ' 0 - i x l x - i y l y = H ' 0 -1.5 ai x -0.5 ai y
【 例 】某建筑场地的地形图和方格网( a =20m)布置如图 1-2-4 所示。该场地系粉质粘土,地面设计泄水坡度为 i x =3‰, i y =2‰。土建设计、生产工艺设计和最高洪水位等方面均无特殊要求,试确定场地设计标高。
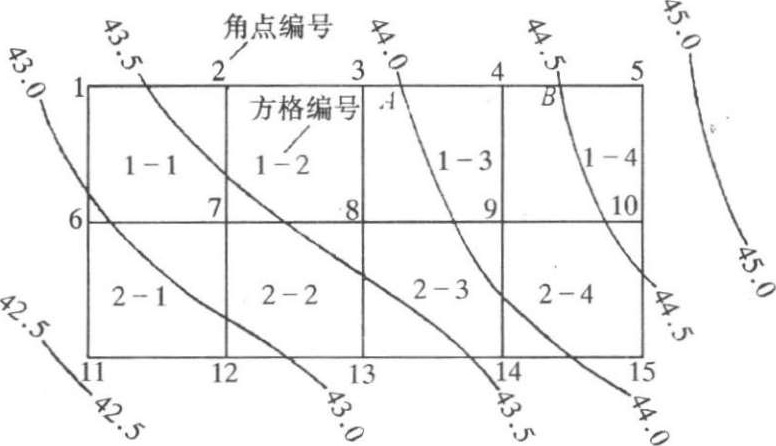
图1-2-4 某建筑场地地形图和方格网布置
【 解 】
①计算角点的自然地面标高
根据地形图上标设的等高线,用插入法求出各方格角点的自然地面标高。
采用插入法时,是假定两等高线之间的地面高低是呈直线变化的。如角点4的地面标高( H 4 ),从图1-2-4中可看出,是处于与两等高线相交的 AB 直线上。由图1-2-5,根据相似三角形特性,可写出:
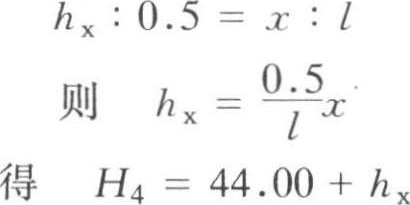
在地形图上,只要量出 x (角点4至44.0 等高线的水平距离)和 l (44.0 等高线和44.5等高线与 AB 直线相交的水平距离)的长度,便可算出 H 4 的数值。但是,这种计算是繁琐的,所以,通常是采用图解法来求得各角点的自然地面标高。如图1-2-6所示,用一张透明纸,上面画出六根等距离的平行线(线条尽量画细些,以免影响读数的准确),把该透明纸放到标有方格网的地形图上,将六根平行线的最外两根分别对准点 A 与点 B ,这时六根等距离的平行线将 A 、 B 之间的0.5m的高差分成五等分,于是便可直接读得角点4的地面标高 H 4 =44.34。其余各角点的标高均可类此求出。
用图解法求得的各角点标高见图1-2-7。
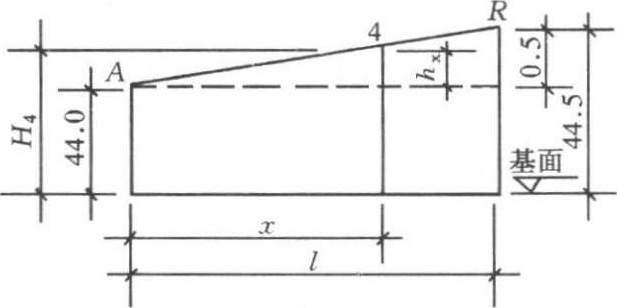
图1-2-5 插入法计算标高简图
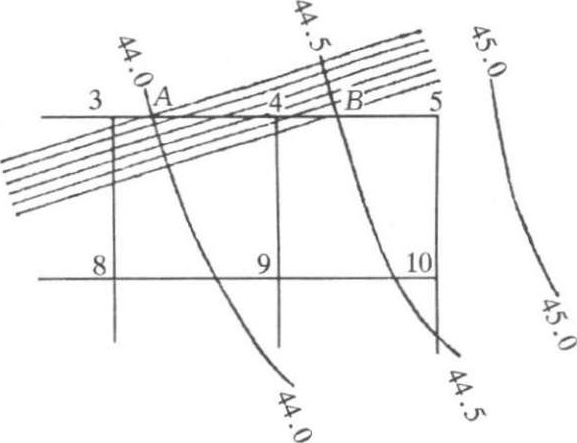
图1-2-6 插入法的图解法

图1-2-7 场地方格网及地面标高
②计算场地设计标高 H 0
∑ H 1 =43.24 + 44.80 + 44.17 + 42.58 =174.79(m)
2∑ H 2 =2 ×(43.67 + 43.94 + 44.34 + 44.67 + 43.67 + 43.23 + 42.90 + 42.94)
=698.72(m)
4∑ H 4 =4 ×(43.35 + 43.76 + 44.17)=525.12(m)
由式(2-2-1),得:
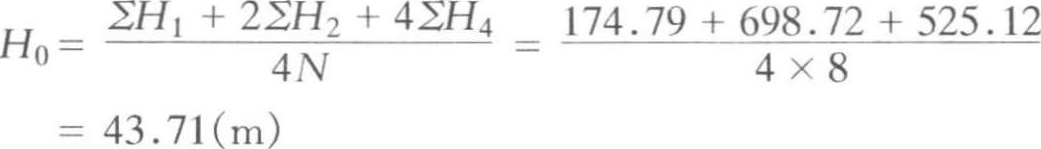
③按照要求的泄水坡度计算各方格角点的设计标高
以场地中心点即角点8为 H 0 (图1-2-7),其余各角点的设计标高为:
H 1 = H 0 -40 ×3‰+ 20 ×2‰=43.71 -0.12 + 0.04 =43.63(m)
H 2 = H 1 + 20 ×3‰=43.63 + 0.06 =43.69(m)
H 6 = H 0 -40 ×3‰±0 =43.71 -0.12 =43.59(m)
H 7 = H 6 + 20 ×3‰=43.59 + 0.06 =43.65(m)
H 11 = H 0 -40 ×3‰-20 ×2‰=43.71 -0.12 -0.04 =43.55(m)
H 12 = H 11 + 20 ×3‰=43.55 + 0.06 =43.61(m)
其余各角点设计标高均可类此求出,详见图1-2-7中的设计标高诸值。
(二)场地土方工程量计算
场地土方量的计算方法,通常有方格网法和断面法两种。方格网法适用于地形较为平坦、面积较大的场地,断面法则多用于地形起伏变化较大或地形狭长的地带。
1.方格网法
方格网法是采用方格网控制整个场地而计算土方量。方格边长取决于地形变化的复杂程度,一般取10m、20m、30m或40m。土方量计算的步骤是:根据每个方格角点的自然地面标高和实际采用的设计标高,算出相应的角点挖填高度(称施工高度),然后计算每一方格的土方量(大规模场地土方量计算,可使用专门的土方工程量计算表),并算出场地边坡的土方量,相加后,即可得到整个场地的挖、填土方总量。
场地各方格的土方量,一般可分为下述三种不同类型进行计算。
(1)方格四个角点全部为填或全部为挖(图1-2-8),其土方量为:
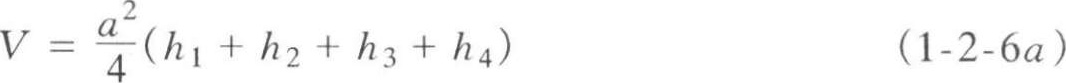
式中 V ——填方或挖方体积(m 3 );
h 1 、 h 2 、 h 3 、 h 4 ——方格角点填挖高度,采用绝对值(m);
a ——方格边长。
若 a =20m, h 以cm为单位代入,则上式可写为:

(2)方格的相邻两角点为挖方,另两角点为填方(图 2-2-9),其挖方部分的土方量为:
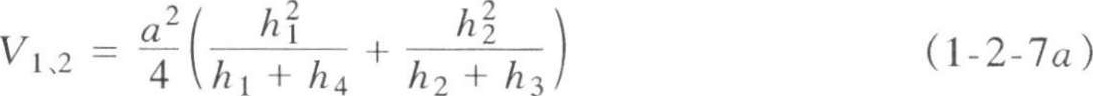
填方部分的土方量为:
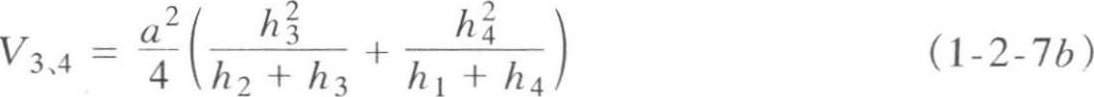
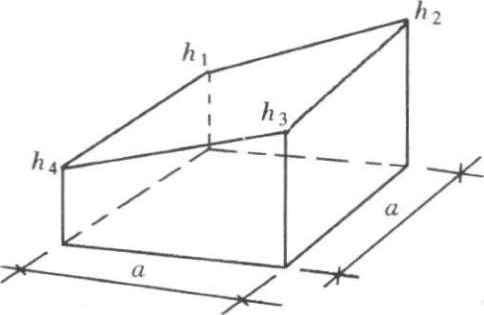
图1-2-8 全挖或全填的方格
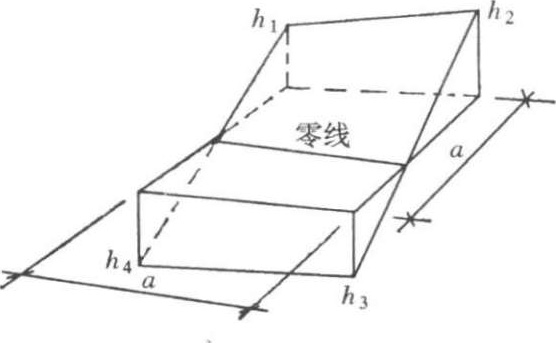
图1-2-9 两挖或两填的方格
(3)方格的三个角点为挖,另一个角点为填(或相反)(图1-2-10),其填方部分的土方量为:
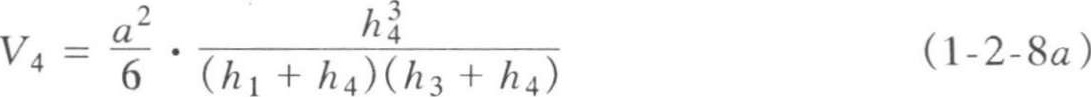
挖方部分的土方量为:
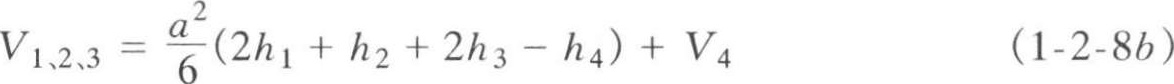
使用上述方格网法计算时应注意:
①使用式(1-2-7)时, h 1 、 h 2 需同在零线的一侧(图1-2-9), h 3 、 h 4 同在零线的另一侧,且 h 1 、 h 2 、 h 3 、 h 4 须依次排序;
②使用式(1-2-8)时,填(或挖)方的一个角点为 h 4 ,其余挖(或填)方的三个角点为 h 1 、 h 2 、 h 3 ,且 h 1 、 h 2 、 h 3 、 h 4 须依次排序。
2.断面法
沿场地的纵向或相应方向取若干个相互平行的断面(可利用地形图定出或实地测量定出),将所取的每个断面(包括边坡)划分成若干个三角形和梯形,如图1-2-11所示。对于某一断面,其中三角形和梯形的面积为:
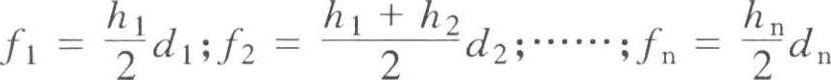
该断面面积为:
F i = f 1 + f 2 + ……+ f n
若
d 1 = d 2 =……= d n = d
则
F i = d ( h 1 + h 2 + ……+ h n )
各个断面面积求出后,即可计算土方体积。设各断面面积分别为 F 1 、 F 2 、……、 F n ,相邻两断面之间的距离依次为 l 1 、 l 2 、……、 l n ,则所求土方体积为:

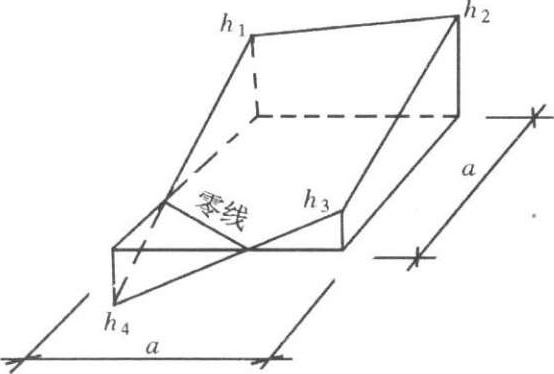
图1-2-10 三挖一填(或相反)的方格
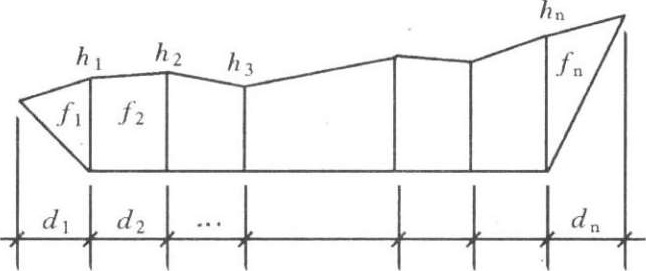
图1-2-11 断面法计算图
如图 1-2-12 所示,是用断面法求面积的一种简便方法,叫“累高法”。此法不需用公式计算,只要将所取的断面绘于普通坐标纸上( d 取等值),用透明纸尺从 h 1 开始,依次量出(用大头针向上拨动透明纸尺)各点标高( h 1 、 h 2 ……),累计得出各点标高之和,然后将此值与 d 相乘,即可得出所求断面面积。
【 例 】某工程场地方格网如图 1-2-7所示,方格边长 20m×20m。试计算挖、填土方工程量。
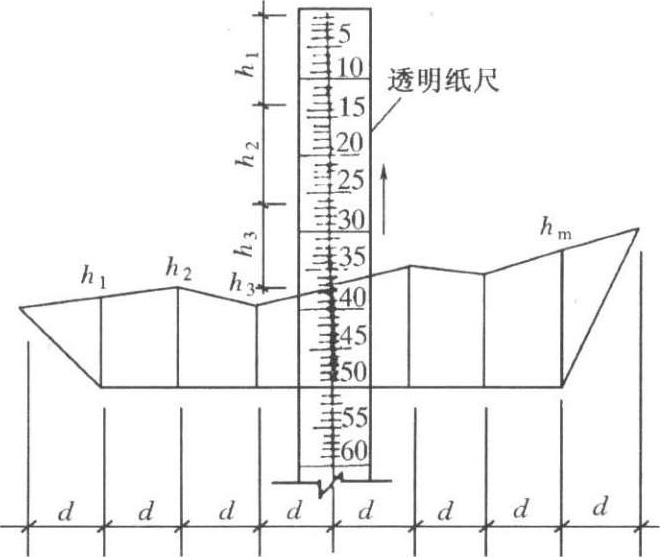
图1-2-12 用累高法求断面面积
【 解 】
①计算各角点的施工高度
各角点的挖方或填方高度,称之为施工高度。习惯上以“+ ”号表示填方,以“-”号表示挖方。施工高度的计算式为:
施工高度( h )=设计标高-自然地面标高
h 1 =43.63 -43.24 =+ 0.39m
h 2 =43.69 -43.67 =+ 0.02m
h 3 =43.75 -43.94 =-0.19m
……
各角点施工高度,见图1-2-7中的施工高度诸值。
②标出“零线”
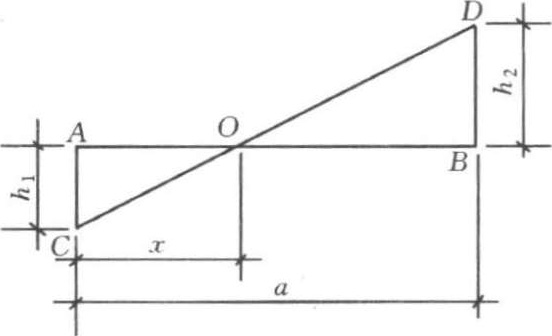
图1-2-13 求零点的图解法
零线即施工高度为零的线,也就是挖方区和填方区的分界线。零线确定的方法是:先求出有关方格某边线(此边线的特点是一端为挖,另一端为填)上的“零点”(不挖不填的点),将相邻的零点连接起来,即为零线(图 1-2-7)。
确定零点的简便方法是图解法。如图 1-2-13所示,用与方格网相应的比例画出直线 AB ,令其等于方格边长 a ,通过 A 、 B ,用另一较大的比例分别绘出 h 1 和 h 2 ( h 1 为填方角点的施工高度, h 2 为挖方角点的施工高度),连接 C 、 D ,其直线交 AB 于 O , O 即为零点。各有关方格边线上的零点图解,如图1-2-14所示。
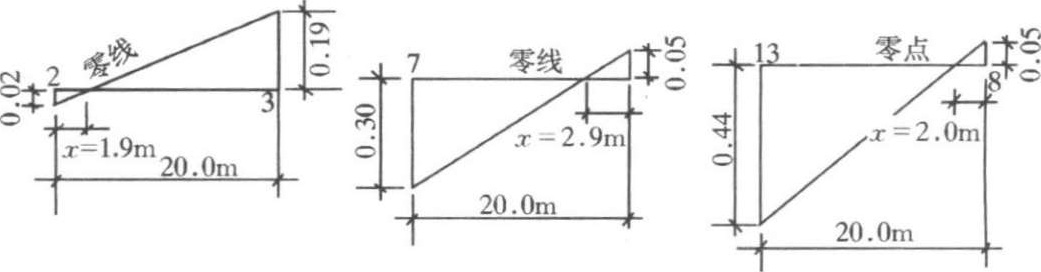
图1-2-14 有关方格边线上的零点图解
③计算土方工程量
第一种类型,即全挖或全填的方格,用式(1-2-6 b )计算,其土方量为:
V 1 -1 = h 1 + h 2 + h 3 + h 4 =39 + 2 + 30 + 65 =(+)136m 3
V 2 -1 =65 + 30 + 71 + 97 =(+)263m 3
V 1 -3 =19 + 53 + 40 + 5 =(-)117m 3
V 1 -4 =53 + 93 + 84 + 40 =(-)270m 3
第二种类型的方格,用式(1-2-7)计算( a 用20m, h 以cm为单位代入),其土方工程量为:
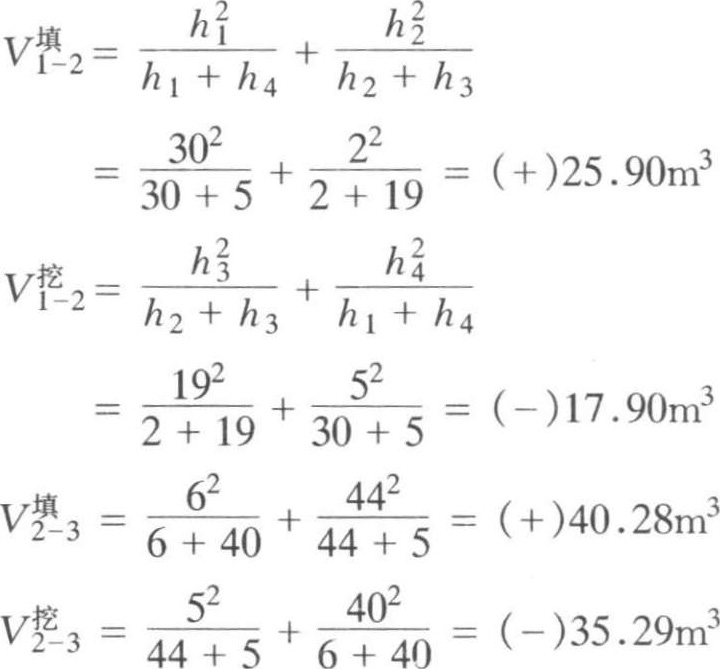
第三种类型的方格,用式(1-2-8)计算,( a 用20m, h 以cm为单位代入),其土方工程量为:
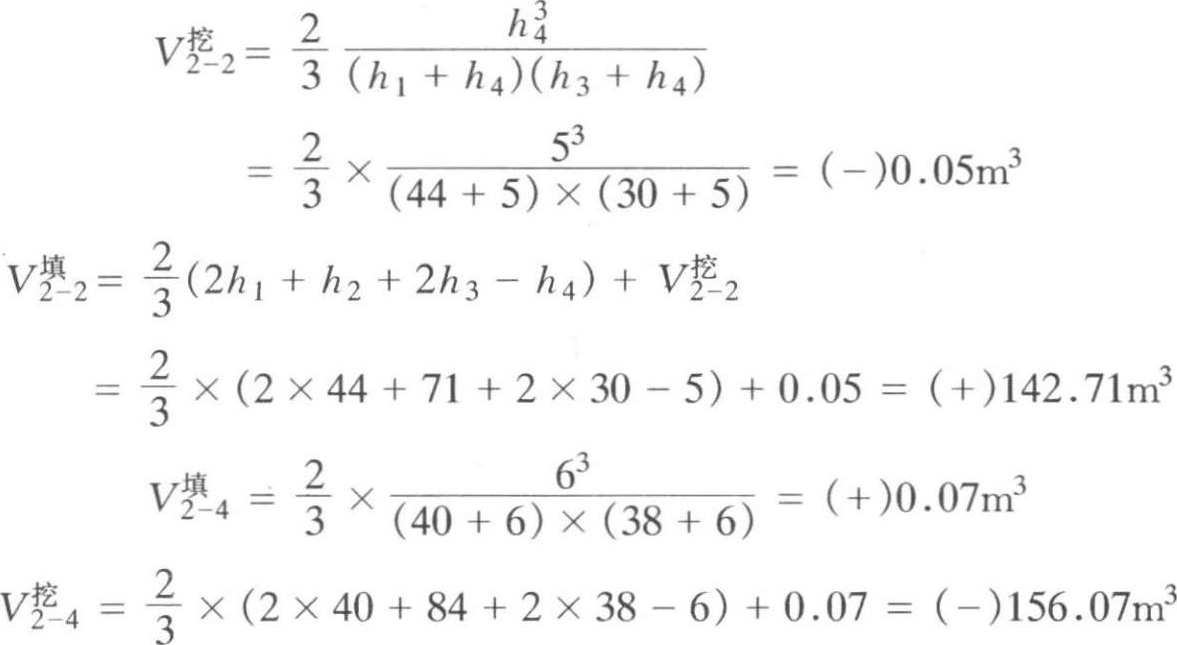
将计算出的土方量填入相应的方格中,如图1-2-7所示。
(三)边坡土方量计算
为了维持土体的稳定,场地的边沿均需作成相应的边坡。图 1-2-15 是一场地边坡的平面示意图。从图中可知,边坡的土方量可以划分为两种几何形体进行计算,一种为三角棱锥体(如体积①~③,⑤~⑪),另一种为三角棱柱体(如体积④)。
1.三角棱锥体边坡体积
如图1-2-15中的①所示,其体积为:

式中 l 1 ——边坡①的长度(m);
F 1 ——边坡①的端部面积(m 2 ),按下式计算:
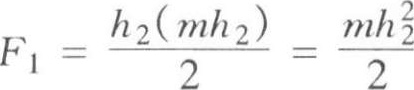
h 2 ——角点的挖土高度(m);
m ——边坡的坡度系数。
2.三角棱柱体边坡体积
如图1-2-15中的④所示,其体积为:
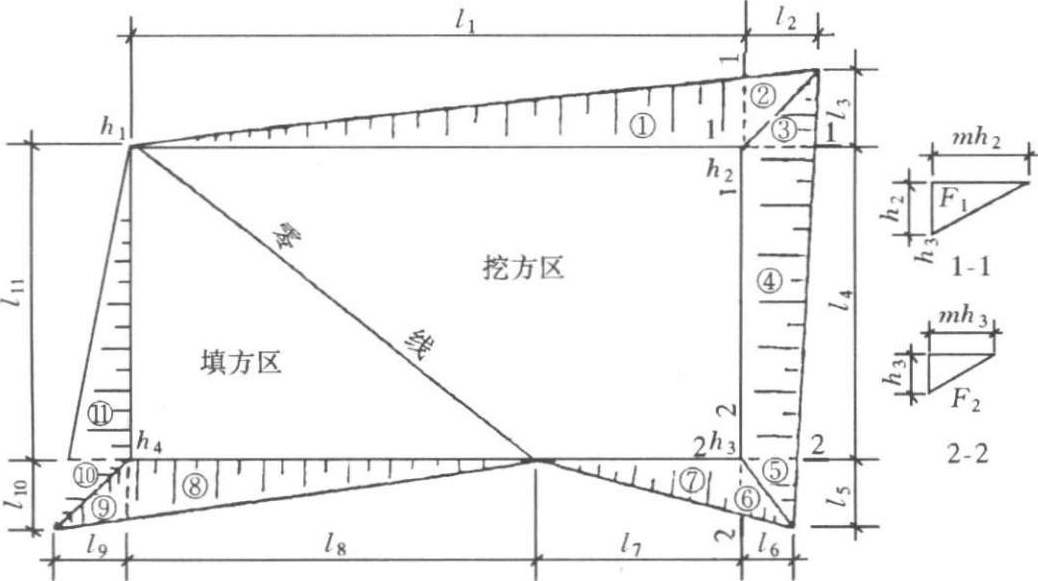
图1-2-15 场地边坡平面图

当两端部面积相差很大的情况下,则可采用式(1-2-12 a )计算其体积。
【 例 】某场地平整工程,如图1-2-16所示。长80m、宽40m,土质为粉质粘土,取挖方边坡坡度为 1∶1.25 ,填方边坡坡度为 1∶1.50。试求边坡挖、填土方量。
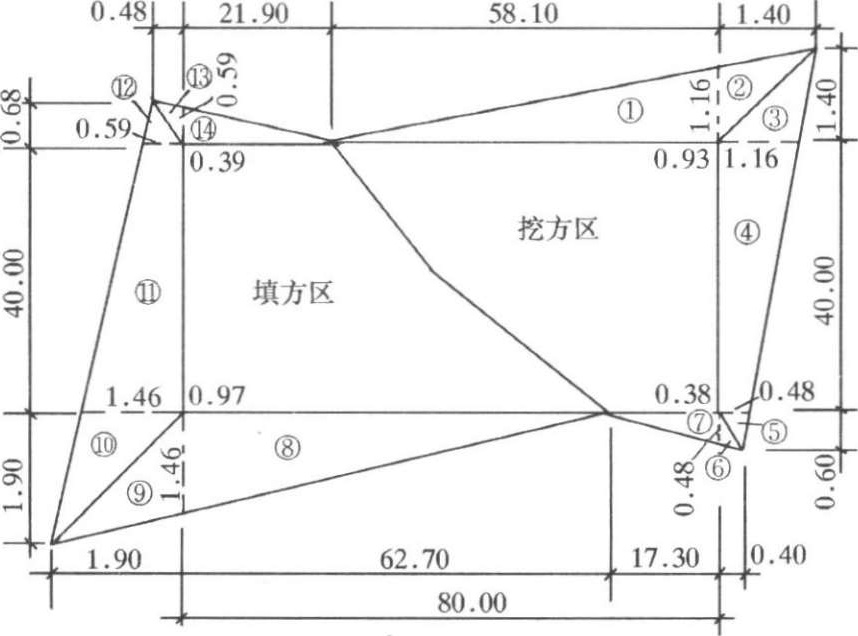
图1-2-16 场地边坡平面轮廓尺寸图
(图中比例:场地1 ∶1000;边坡1∶100)
【 解 】先求边坡角点5、15、1、11 的挖、填方宽度:
角点5 (图1-2-7,下同)挖方宽度 0.93 ×1.25 =1.16m
角点 15 挖方宽度 0.38 ×1.25=0.4 8 m
角点 1 填方宽度 0.39 ×1.50 =0.59m
角点 11 填方宽度 0.97 ×1.50=1.4 6 m
按照计算出的场地轮廓四个角点的边坡宽度,绘出边坡平面轮廓尺寸,如图 1-2-16 所示。边坡土方量,可划分为三角棱锥体和三角棱柱体两种类型,按式(1-2-10)、式(1-2-11)计算。挖方区边坡土方量:
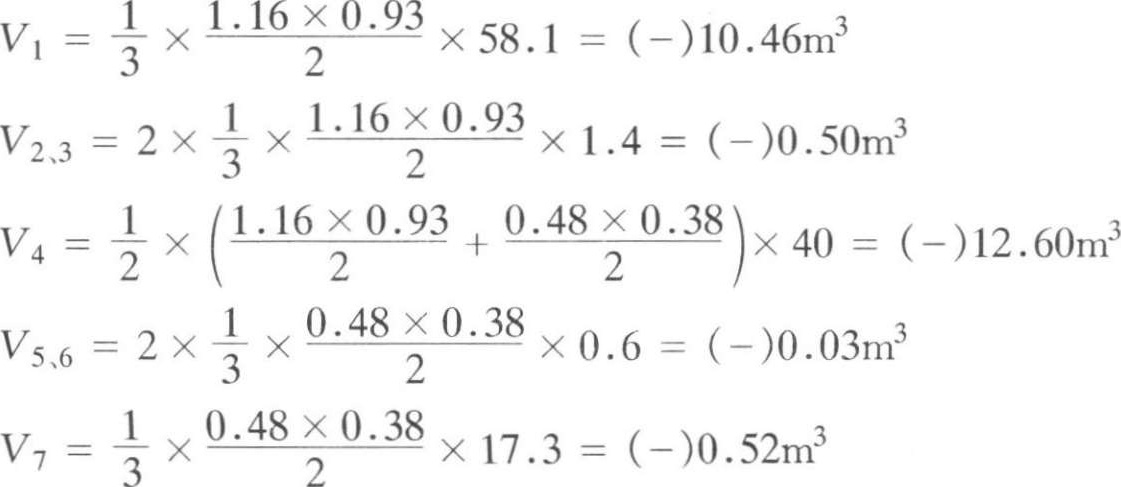
挖方区边坡土方量合计:
V 挖 =-(10.46+0.50+12.60+0.03+0.52)=(-)24.11m 3
填方区边坡土方量(算式从略):
V 8 =+14.80m 3
V 9 、10 =+0.90m 3
V 11 =+ 16.5m 3
V 12 、13 =+ 0.04m 3
V 14 =+ 0.80m 3
填方区边坡土方量合计:
V 填 =+14.80+0.90+16.50+0.04+0.80=(+)33.04m 3
基坑土方量可按立体几何中的拟柱体(由两个平行平面做上下底的一种多面体)体积(图 1-2-17)公式计算。即

或
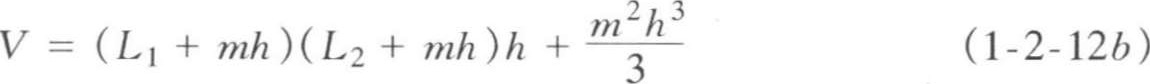
式中 F 1 、 F 2 ——基坑上下底面积(m 2 );
F 0 ——基坑中部面积(m 2 );
h ——基坑开挖深度(m);
L 1 、 L 2 ——基坑上、下口的长边尺寸(m);
m ——基坑边坡坡度系数。
基槽(图1-2-18)和路堤土方量,可以沿着其长度方向分段,用下式逐段计算。即

式中 V i ——第 i 段土方量(m 3 );
F 1 、 F 2 ——第 i 段两端的面积(m 2 );
F 0 ——第 i 段中部面积(m 2 );
L i ——第 i 段长度(m)。
将各段土方量相加,即可得总土方量。即:

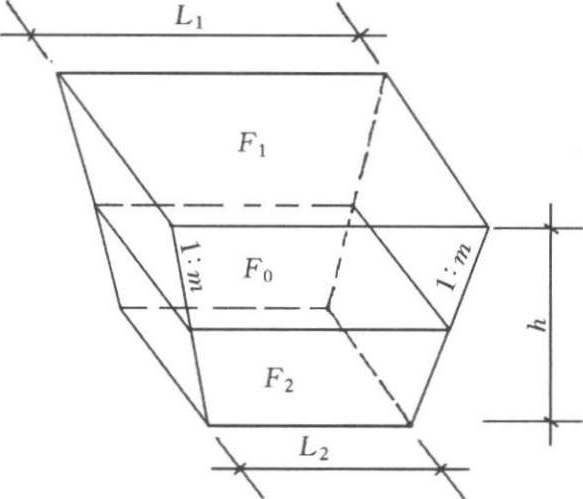
图1-2-17 基坑土方量计算图
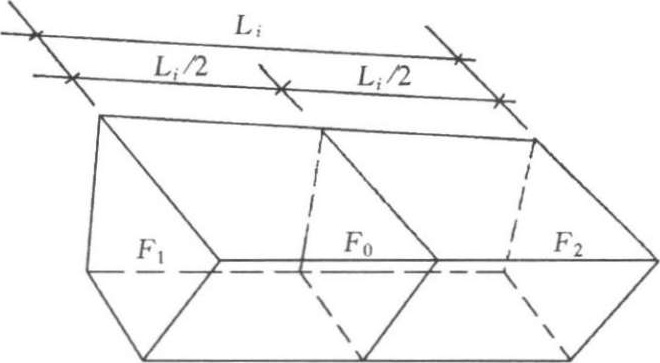
图1-2-18 基槽土方量计算图