




对离散型随机变量进行完整的描述,需要指定随机变量的可能取值以及与每个取值的概率.
例 3.2.1 某公司为调查汽车销量情况,现抽取 100 天的汽车销售量(表 3.2),其中 X 表示每天销售的汽车台数.由相对频率法,得到随机变量 X 的概率分布,即 X 的可能取值为0,1,2,这些取值相应的概率分别为 0.2,0.6,0.2.它完整地描述了随机变量 X 的分布信息,称为离散型随机变量 X 的概率分布.
表 3.2
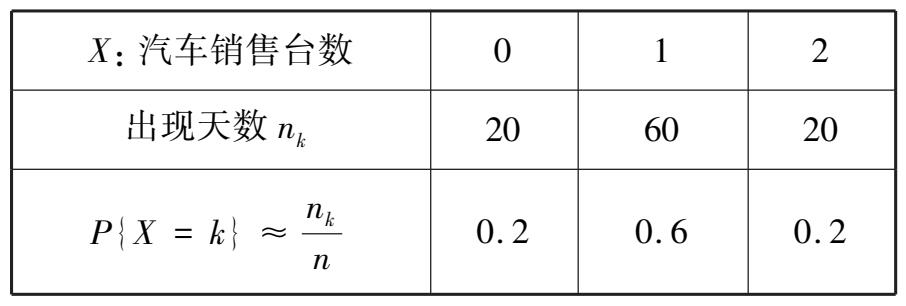
定义 3.2.1 若随机变量 X 所有可能取值是有限个或无限可列个,即 X = x k ( k = 1,2,…),则称随机变量 X 为 离散型随机变量 (Discrete Random Variable,简记为D. R. V).称
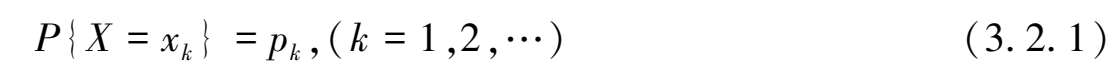
为离散型随机变量 X 的 概率分布 或 分布律 .分布律常用表 3.3 表示.
表 3.3

由概率的定义, p k 满足以下两个性质:
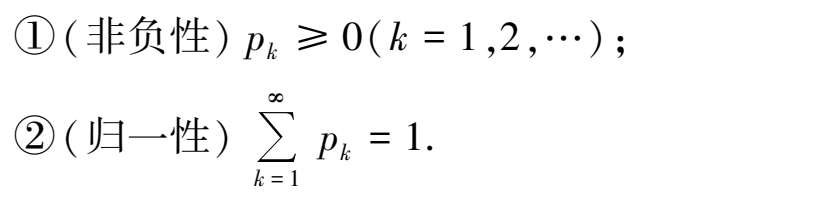
反之,任意一个具有以上两个性质的数列{ p k }( k = 1,2,…),一定可以作为某个离散型随机变量的分布律.为了直观地表达分布律,作分布律图,如图 3.3 所示,其中 x k 处垂直于 x 轴的线段高度为 p k ,它表示 X 取 x k 的概率值.
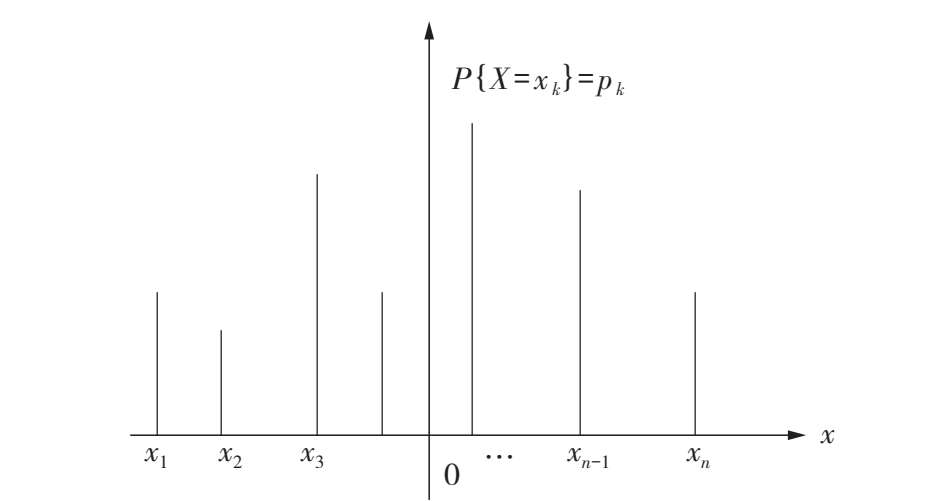
图 3.3
随机事件{ X = x n } = { ω X ( ω ) = x n },且互不相容.如果 X ( e 1 ,…, e k ) = x n ,则 P { X = x n } = P { e 1 ,…, e k }.
例 3.2.2 某投资者计划投资某大型股票基金或政府长期债券基金.理财顾问认为未来的经济形势可能有 4 种情形:衰退、缓慢增长、稳定增长、快速增长,预期概率分别为:
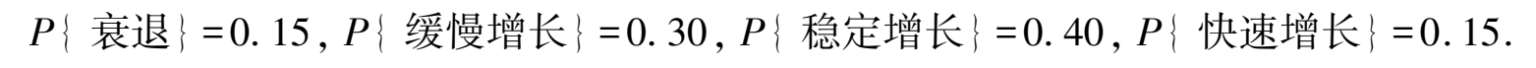
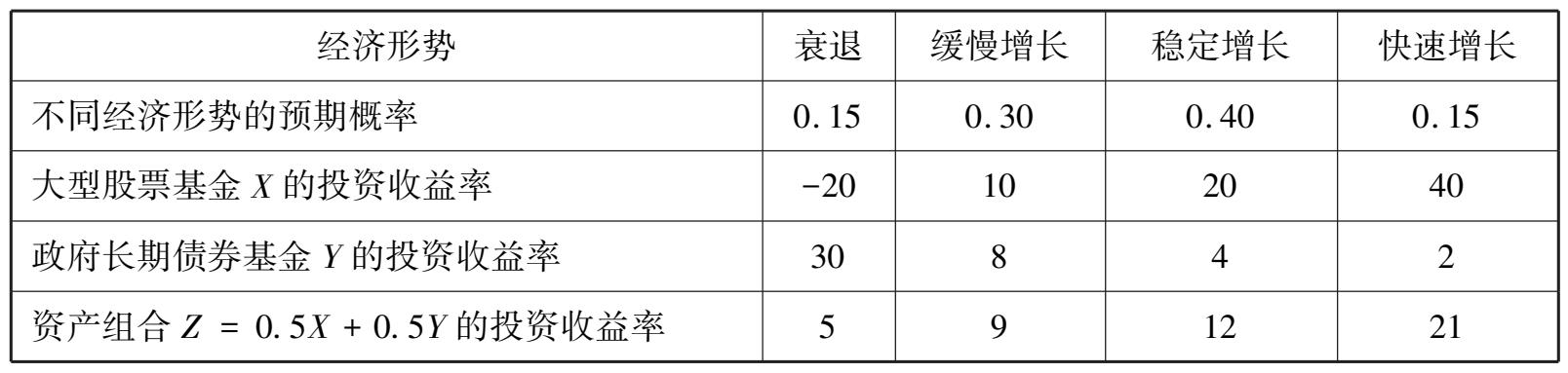
为在收益和风险之间寻求平衡,理财顾问建议投资者把大型股票基金和政府长期债券各购买一半.该投资者根据不同经济形势下的实际收益情况,制订表 3.4,其中,随机变量 X 表示大型股票基金的投资收益率,随机变量 Y 表示政府长期债券基金的投资收益率,随机变量 Z 表示资产组合 0.5 X + 0.5 Y 的投资收益率.该表给出了离散型随机变量 X , Y , Z 的概率分布.
表 3.4 收益率
单位:%
有些离散型随机变量的概率分布比较容易得到,而且许多不同研究领域的随机变量具有相同的特点.根据试验的类型将随机变量进行分类,推导出每种类型的概率分布,并借助数学软件简化计算.第 4 章将详细给出不同类型随机变量的概率分布及其性质.
设离散型随机变量 X 的分布律见表 3.3.由分布函数的定义可知
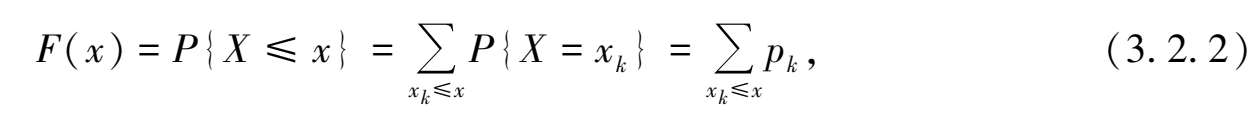
此处的和式
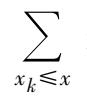 表示对所有满足
x
k
≤
x
的
k
求和,形象地讲就是对那些满足
x
k
≤
x
所对应的
p
k
累加.
表示对所有满足
x
k
≤
x
的
k
求和,形象地讲就是对那些满足
x
k
≤
x
所对应的
p
k
累加.
例 3.2.3 根据例 3.2.1 中随机变量 X 的分布律,计算以下结果:
(1)求事件{ X ≤ 0},{ X < 2},{-2 ≤ X ≤ 6}的概率.
(2)求随机变量 X 的分布函数,并用图形表示.
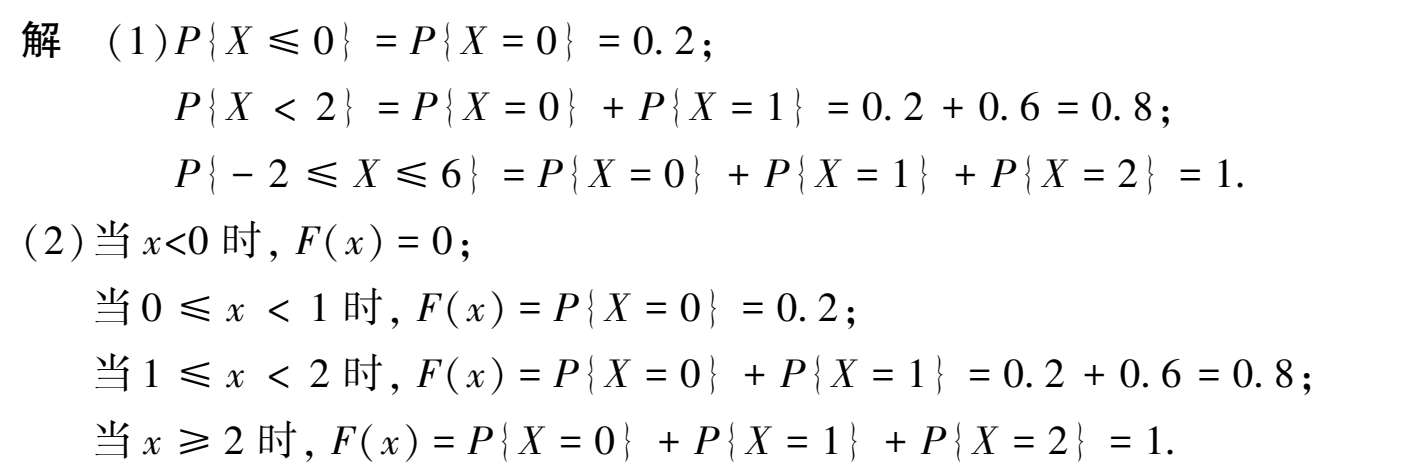
综上所述,
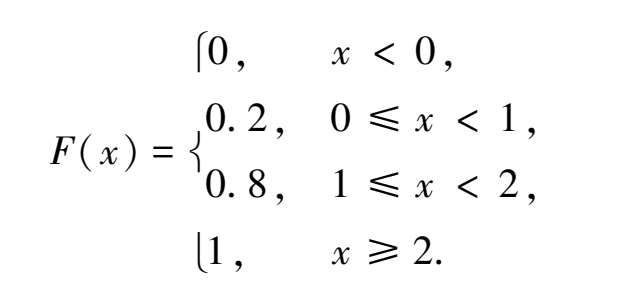
分布函数 F ( x )的图形如图 3.4 所示,它是一条阶梯状右连续曲线,在 x = 0,1,2 处有跳跃,其跳跃高度分别为 0.2,0.6,0.2,这条曲线从左至右依次从 F ( x ) = 0 逐步升级到 F ( x ) = 1.
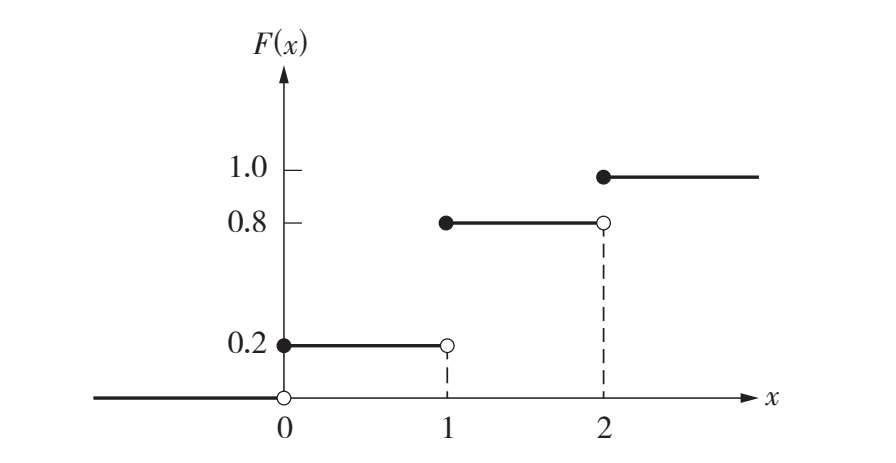
图 3.4
定义一个随机变量及其概率分布的最大好处是,一旦掌握其概率分布,决策者对各种感兴趣事件的概率计算就变得相对简单.设离散型随机变量 X 的分布律见表 3.3,可归纳出 X 的以下性质.
①随机变量 X 落在实数轴上任何区间[ a , b ]上的概率都表示为
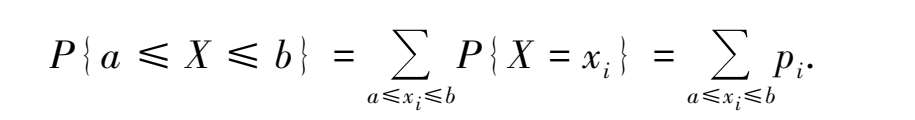
②用式(3.2.2)可求出随机变量 X 的分布函数 F ( x ),它是一个右连续函数.从图像上看,分布函数 F ( x )表示一条阶梯状右连续曲线,在 X = x k ( k = 1,2,…)处有跳跃,跳跃的高度恰为 p k = P { X = x k },从左至右,由水平直线 F ( x ) = 0 分别按阶高 p 1 , p 2 ,…升至水平直线 F ( x ) = 1.
③若已知离散型随机变量 X 的分布函数 F ( x ),则 X 的分布律也可由分布函数所确定,
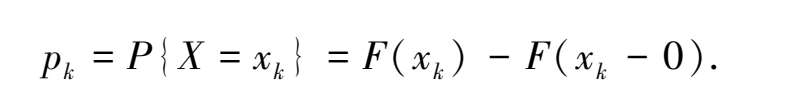
设 X 是离散型随机变量, Y = g ( X )是 X 的函数.则 Y = g ( X )也是离散型随机变量,其概率分布由 X 的概率分布所确定.
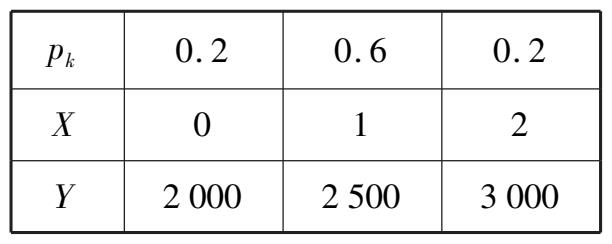
例 3.2.4 在例 3.2.1 中,若员工每个月的工资采用底薪加提成的方式:底薪 2 500 元,保底销量为一台,在此基础上每增加一台得到提成 500 元.工资用随机变量 Y 表示,则 Y 是销售额 X 的函数, Y = 2 500 + 500( X - 1)是一个新的随机变量.求 Y 的概率分布.
解 代入销售额 X 的概率分布,可得工资 Y 的概率分布,见表 3.5.
表 3.5
例 3.2.5 设随机变量 X 分布律见表 3.6,求随机变量函数 Y = ( X - 1) 2 的分布律.
表 3.6

解 随机变量 X 和 Y 的对应关系见表 3.7.
表 3.7

求 Y 取每个值的概率.
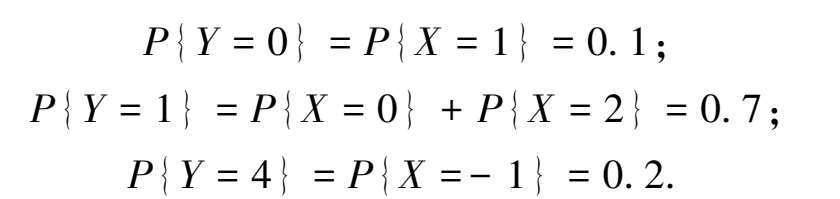
随机变量函数 Y 的分布律见表 3.8.
表 3.8
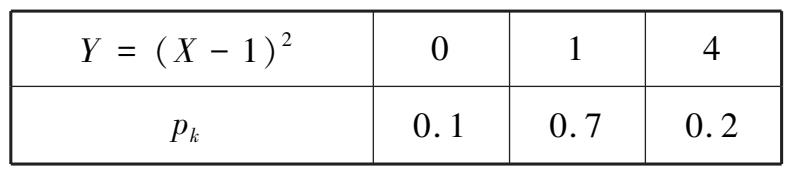
例 3.2.4 和例 3.2.5 中的问题归结为,已知离散型随机变量 X 的概率分布,求随机变量函数 Y = f ( X )的概率分布.具体方法是,分别求出随机变量 X 每一个值对应的 Y 值,取值不相同的项概率不变,取值相同项的概率做加法.