




首先,我发现,如果问题只涉及三条、四条或五条线段,那么,所求的点可以用初等几何学的知识来解决,即仅使用圆规、直尺和我前文中解释过的定理,但是五条线段皆平行的情况除外。对于五条线段皆平行的特殊情况,以及给定六条、七条、八条或九条线段的情况,总能利用与立体轨迹
 相关的几何学知识找到所求的点,即利用三种圆锥曲线中的一种,但是九条线段皆平行的情况除外。对于九条线段皆平行的特殊情况,以及给定十条、十一条、十二条或十三条线段的情况,必须利用比上一条圆锥曲线高一级的曲线,才可找到所求的点,但是十三条线段皆平行的情况除外。对于十三条线段皆平行的特殊情况,以及给定十四条、十五条、十六条或十七条线段的情况,必须利用比上一条圆锥曲线高一级的曲线。以此类推。
相关的几何学知识找到所求的点,即利用三种圆锥曲线中的一种,但是九条线段皆平行的情况除外。对于九条线段皆平行的特殊情况,以及给定十条、十一条、十二条或十三条线段的情况,必须利用比上一条圆锥曲线高一级的曲线,才可找到所求的点,但是十三条线段皆平行的情况除外。对于十三条线段皆平行的特殊情况,以及给定十四条、十五条、十六条或十七条线段的情况,必须利用比上一条圆锥曲线高一级的曲线。以此类推。
其次,我发现,当仅给定三条或四条线段时,所求的点不仅会全部落在其中一种圆锥曲线上,而且有时还会落在一个圆周上,甚至是落在一条直线上
 。
。
当给定五条、六条、七条或八条线段时,所求的点落在仅比圆锥曲线高一级的曲线上,我们不难想象出这种满足条件的曲线。当然,所求的点也可能落在一个圆锥截面,一个圆,或一条直线上。当给定九条、十条、十一条或十二条线段时,所求曲线只比前面的曲线高一级,但任何此类曲线都可以满足条件。以此类推至无限。
最后,圆锥曲线之后第一条也是最简单的一条曲线,是由抛物线与直线相交而生成的,下文将描述其相交的方式。
至此,我相信我已经完成了帕普斯所说的古人尚未完成的工作。接着,我将尝试用几句话来证明,因为我不想再耗费过多笔墨。
在图1-5中,令
AB
、
AD
、
EF
、
GH
,…为给定位置的任意多条线段
 ,求点
C
,使得由它引出的线段
CB
、
CD
、
CF
、
CH
,…与给定线段所成的角分别为∠
CBA
、∠
CDA
、∠
CFE
、∠
CHG
,…,且其中几条线段的乘积等于其余线段的乘积,或者,至少这两个乘积成一定比例——这一条件并不会增加问题的难度。
,求点
C
,使得由它引出的线段
CB
、
CD
、
CF
、
CH
,…与给定线段所成的角分别为∠
CBA
、∠
CDA
、∠
CFE
、∠
CHG
,…,且其中几条线段的乘积等于其余线段的乘积,或者,至少这两个乘积成一定比例——这一条件并不会增加问题的难度。
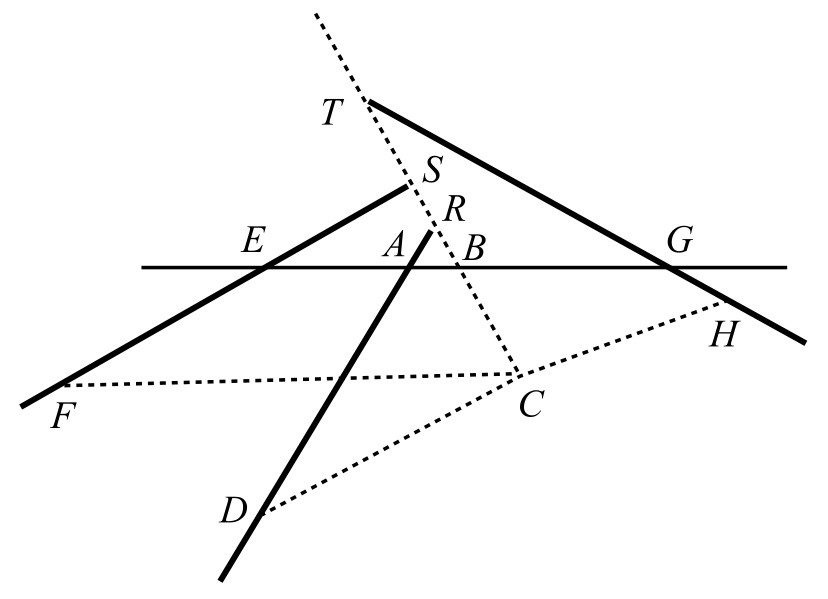
(图1-5)