下载掌阅APP，畅读海量书库
立即打开
1. 电阻的串联
将两个或两个以上的电阻器，一个接一个地依次连接起来，组成无分支的电路，使电流只有一条通道的连接方式叫作电阻的串联。 如图1-6a所示为由三个电阻构成的串联电路。
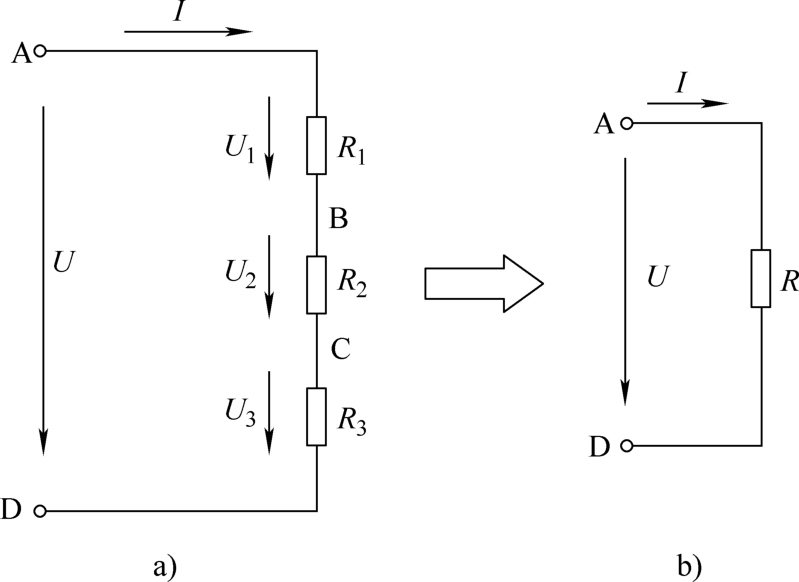
图1-6 电阻的串联及其等效电路
a）串联电路 b）串联电路的等效电路
（1）串联电路的基本特点
1） 串联电路中流过每个电阻的电流都相等 ，即
I = I 1 = I 2 = I 3 =…= I n
2） 串联电路两端的总电压等于各电阻两端的电压 （即各电阻上的电压降） 之和 ，即
U = U 1 + U 2 + U 3 +…+ U n
（2）串联电路的总电阻
在分析串联电路时，为了方便起见，常用一个电阻来表示几个串联电阻，这个电阻称为串联电路的总电阻（又称等效电阻），如图1-6b所示。
用 R 代表串联电路的总电阻， I 代表串联电路的电流，在图1-6中，总电阻应该等于总电压 U 除以电流 I ，即
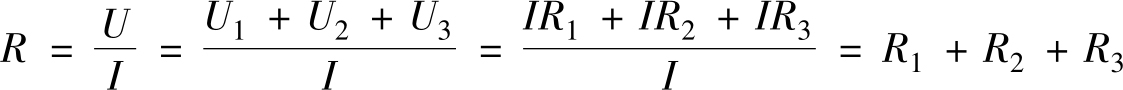
也就是说，串联电路的总电阻等于各个电阻之和。同理，可以推导出
R = R 1 + R 2 + R 3 +…+ R n
2. 电阻的并联
把两个或两个以上的电阻并列连接在两点之间，使每一个电阻两端都承受同一电压的连接方式叫作电阻的并联。 图1-7a所示电路是由三个电阻构成的并联电路。
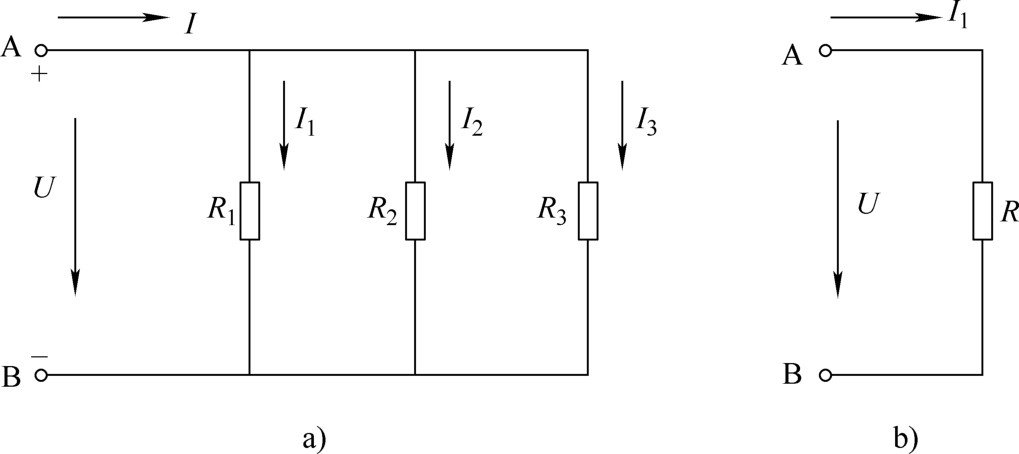
图1-7 电阻的并联及其等效电路
a）并联电路 b）并联电路的等效电路
（1）并联电路的基本特点
1） 并联电路中，各电阻 （或各支路） 两端的电压相等，并且等于电路两端的电压 ，即
U = U 1 = U 2 = U 3 =…= U n
2） 并联电路中的总电流等于各电阻 （或各支路） 中的电流之和 ，即
I = I 1 + I 2 + I 3 +…+ I n
（2）并联电路的总电阻
在分析并联电路时，为了方便起见，常用一个电阻来表示几个并联电阻，这个电阻称为并联电路的总电阻（又称等效电阻），如图1-7b所示。
用 R 代表并联电路的总电阻， U 代表并联电路各支路两端的电压，在图1-7中，根据欧姆定律可得
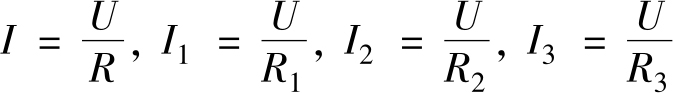
因为
I = I 1 + I 2 + I 3
即
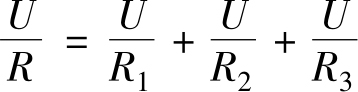
所以
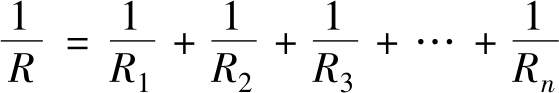
1）当只有两个电阻并联时，可得
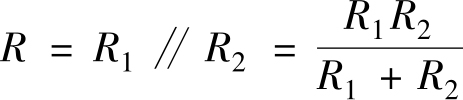
上式中的“∥”是并联符号。
2）若并联的 n 个电阻值都是 R 0 ，则
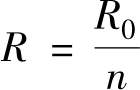
可见，并联电路的总电阻比任何一个并联电阻的阻值都小。