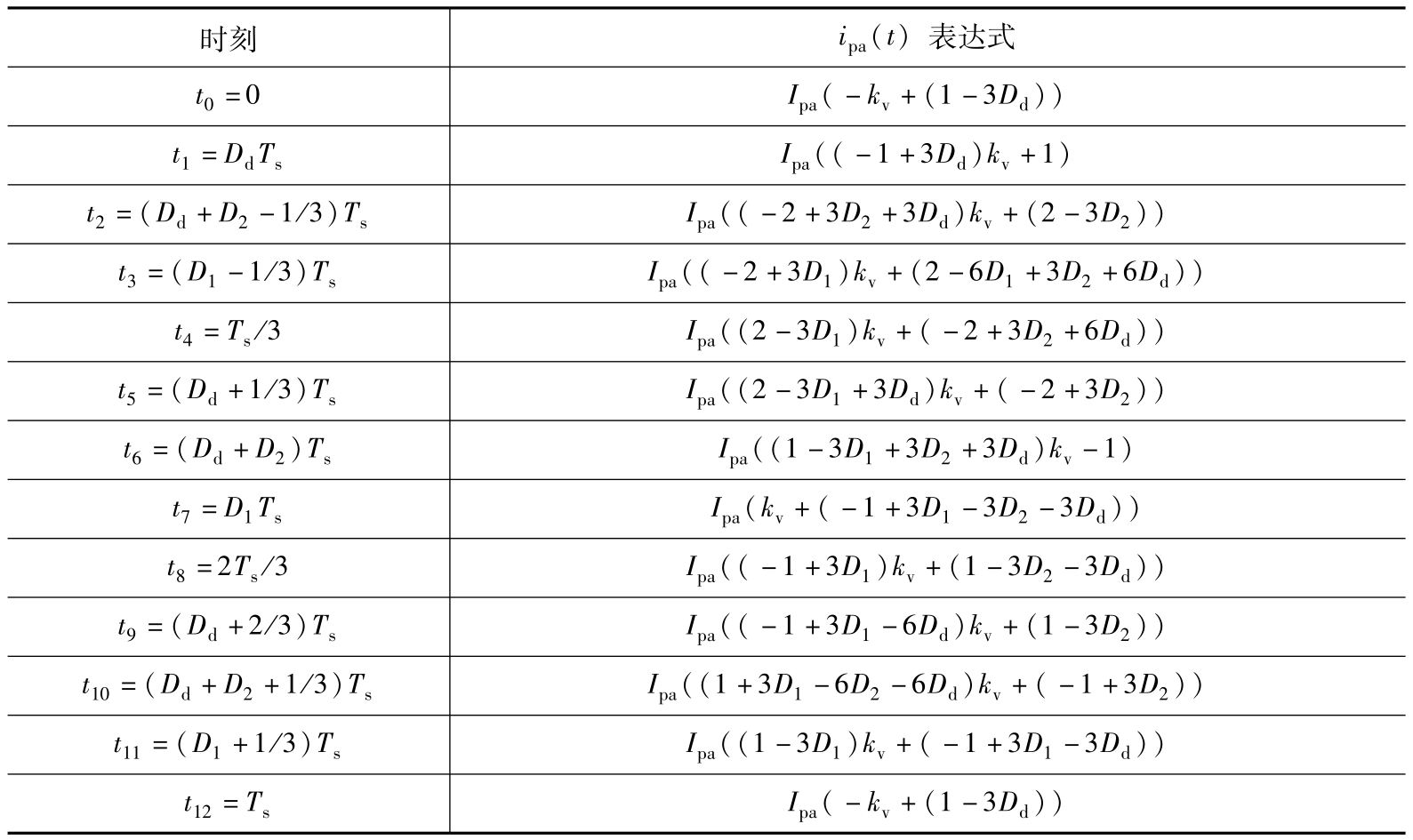
非对称占空比调制策略下,T 2 -DAB变换器中压侧串联式三相桥电路电压波形如图3.4所示。三相半桥中上管Q 1 、Q 3 、Q 5 占空比相同,设为 D 1 ,上下管驱动互补。Q 3 驱动信号的相位较Q 1 滞后120°,Q 5 驱动信号相位较Q 1 超前120°。根据2.1.1节中的式(2.8),串联式三相桥中隔直电容 C da 、 C db 与 C dc 的电压不随开关管占空比的变化而变化,仍分别保持 V M /3、0与 -V M /3,因此B相隔直电容依旧可以省去。由于三相驱动信号互相交错120°,电压 v B′N 与 v C′N 波形与 v A′N 类似,分别滞后和超前120°,下面以 v A′N 为例说明,随着 D 1 取值的变化, v A′N 波形也不同,可以分为3种模态:①当0≤ D 1 <1/3时, v A′N 如图3.4a所示,分别包含2 V 1 、0和 -V 1 三个电平,其中 V 1 = V M /9,以简化后续说明,2 V 1 与 -V 1 电平的持续时间均为 D 1 T s ;②当1/3≤ D 1 <2/3时, v A′N 波形包含2 V 1 、 V 1 、 -V 1 、-2 V 1 四个电平,各电平时间如图3.4b所示;③当2/3≤ D 1 <1时, v A′N 波形如图3.4c所示,分别包含 V 1 、0和-2 V 1 三个电平。
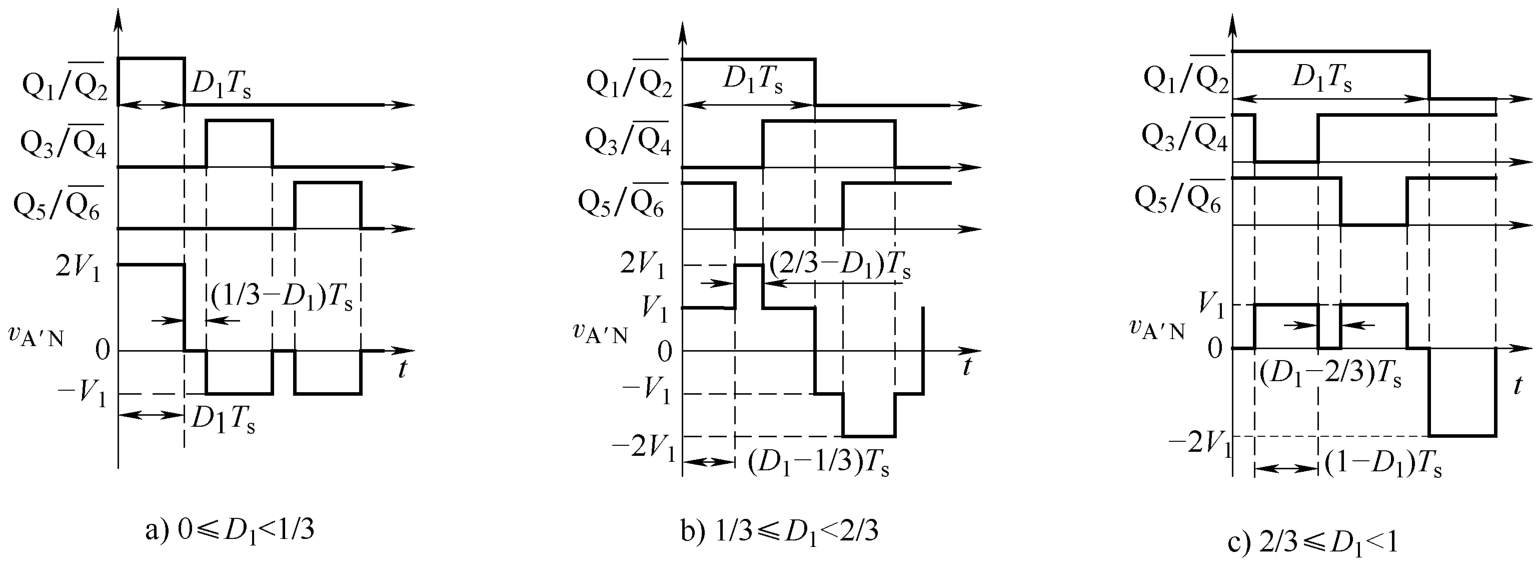
图3.4 非对称占空比调制策略下串联式三相桥电压波形
对于T 2 -DAB变换器的低压侧三相桥,其非对称占空比调制下的交流电压 v an ~ v cn 波形与串联式三相桥中的 v A′N ~ v C′N 相同,也随着其上管S 1 、S 3 、S 5 的占空比 D 2 的变化分为三种情况:0≤ D 2 <1/3、1/3≤ D 2 <2/3和2/3≤ D 2 <1,如图3.5所示,其中 V 2 = V L /3以简化后续说明与推导。
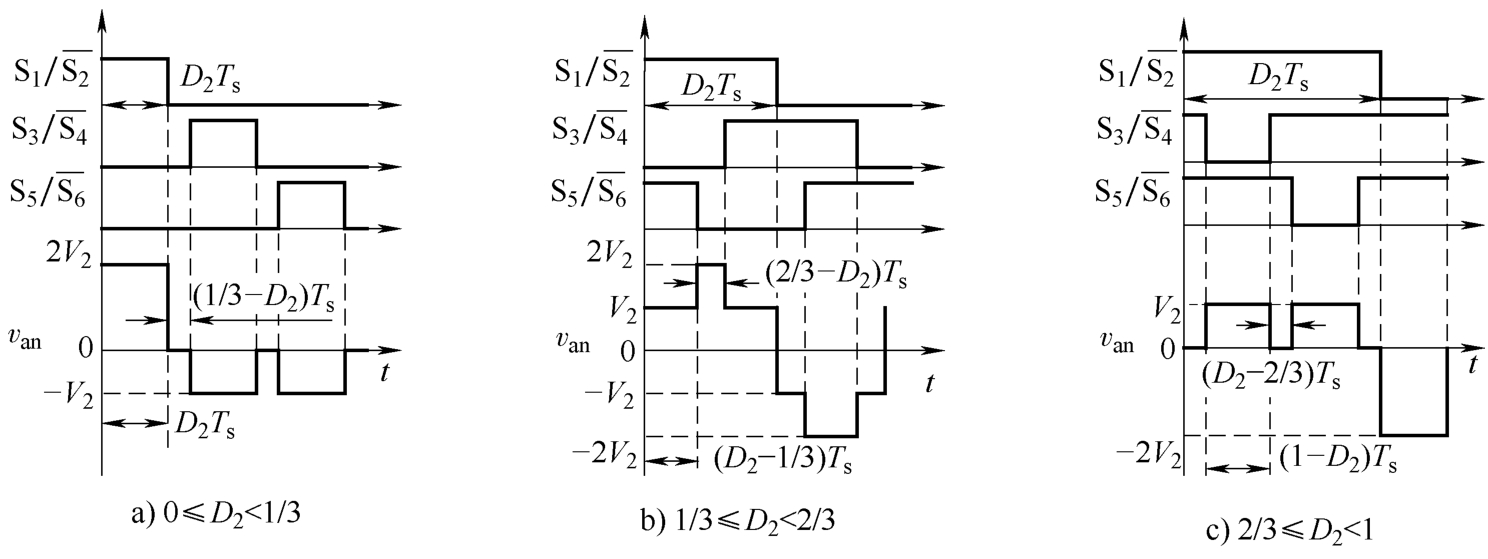
图3.5 非对称占空比调制策略下并联式三相桥电压波形
在中、低压侧三相桥非对称占空比调制的基础上,采用移相控制调节传输功率控制端口电压,可得非对称占空比移相混合控制策略。该混合控制策略下的T 2 -DAB变换器典型工作波形如图3.6所示,通过调节占空比 D 1 与 D 2 ,可调节开关管的开通电流[如图3.6中 i pa ( t 0 )],从而实现ZVS开通,减少开关损耗。另一方面,对于DAB变换器,较大开通电流将使得回流功率增大,从而增大电流应力,导致较高的开关管导通损耗与变压器绕组损耗。因此需要根据不同的端口电压与传输功率,对占空比 D 1 、 D 2 以及移相角进行优化,同时保证实现ZVS开通与减小电流应力,从而提升变换效率。此处,为便于后续分析,将开关管S 1 驱动信号滞后开关管Q 1 的时间定义为移相时间 D d T s , D d 则为移相占空比。
为优化控制变量,需要对变换器进行数学建模,目前主要有两种建模方法:时域分析建模(Time-Domain Analysis,TDA)方法与谐波分析建模(Harmonic Component Analysis,HCA)方法。在TDA方法中,首先要对变换器工作模态进行时域分析,分别建立不同工作模态中关键电压、电流的数学模型,在此基础上建立目标函数与约束条件进行优化。在HCA方法中,一般需将开关管开关函数以傅里叶级数形式表示,在此基础上推导关键电压、电流的傅里叶级数表达式,从而建立目标函数与约束条件并进行优化。HCA方法避免了TDA方法中复杂的模态分析过程,但是其精确性依赖于所分析的谐波最高次数,在现有文献中一般最高取三次谐波分析,以降低计算量。然而,在轻载与电压不匹配情况下,由于谐波含量大幅上升,基于三次谐波分析的HCA建模准确度大幅下降,从而导致错误优化结果。因此,为了保证优化结果的精确性,本章采用TDA方法对T 2 -DAB变换器进行建模。
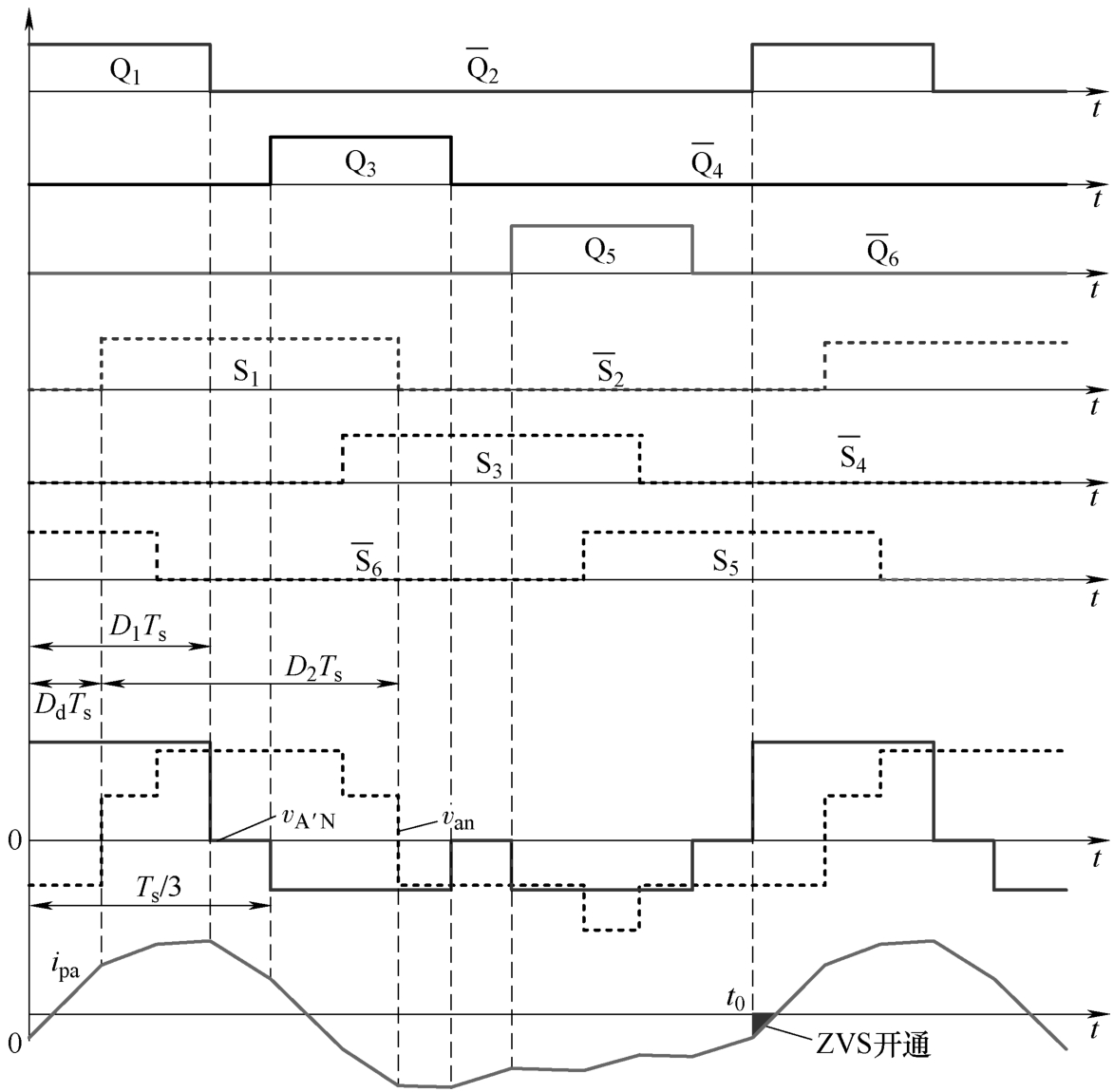
图3.6 非对称占空比移相混合控制下T 2 -DAB变换器典型工作波形
基于3.2.1节分析,非对称占空比调制下的中、低压侧三相桥各具有三种工作模态,因此 D 1 与 D 2 的组合共有9种情况。不失一般性地,以1/3< D 1 <2/3、1/3< D 2 <2/3情况为例进行建模分析。如图3.7a所示,当 D 1 -D 2 >0、 D 1 + D 2 ≤1时, v A′N 的 V 1 与-2 V 1 电平阶段的持续时间[即( D 1 -1/3) T s ],长于 v an 的 V 2 与-2 V 2 电平阶段的持续时间[即( D 2 -1/3) T s ],但短于其2 V 2 与 -V 2 阶段持续时间[即(2/3 -D 2 ) T s ]。以此方法可将1/3< D 1 <2/3、1/3< D 2 <2/3工况分为4种类型:① D 1 -D 2 >0, D 1 + D 2 ≤1;② D 1 -D 2 ≤0, D 1 + D 2 ≤1;③ D 1 -D 2 ≤0, D 1 + D 2 >1;④ D 1 -D 2 >0, D 1 + D 2 >1,其交流电压 v A′N 与 v an 波形分别如图3.7所示。
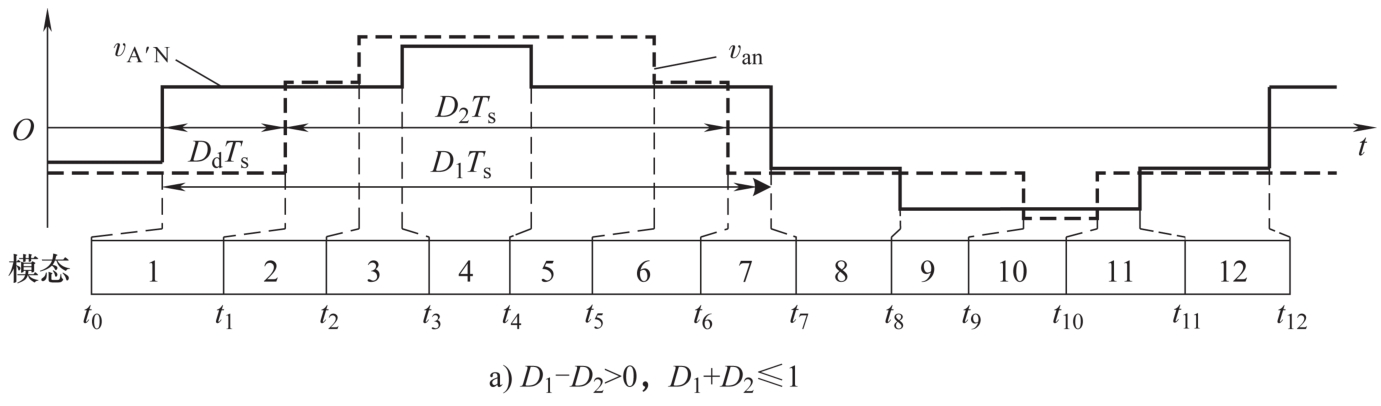
图3.7 不同 D 1 与 D 2 情况下的电压 v A′N 与 v an 波形
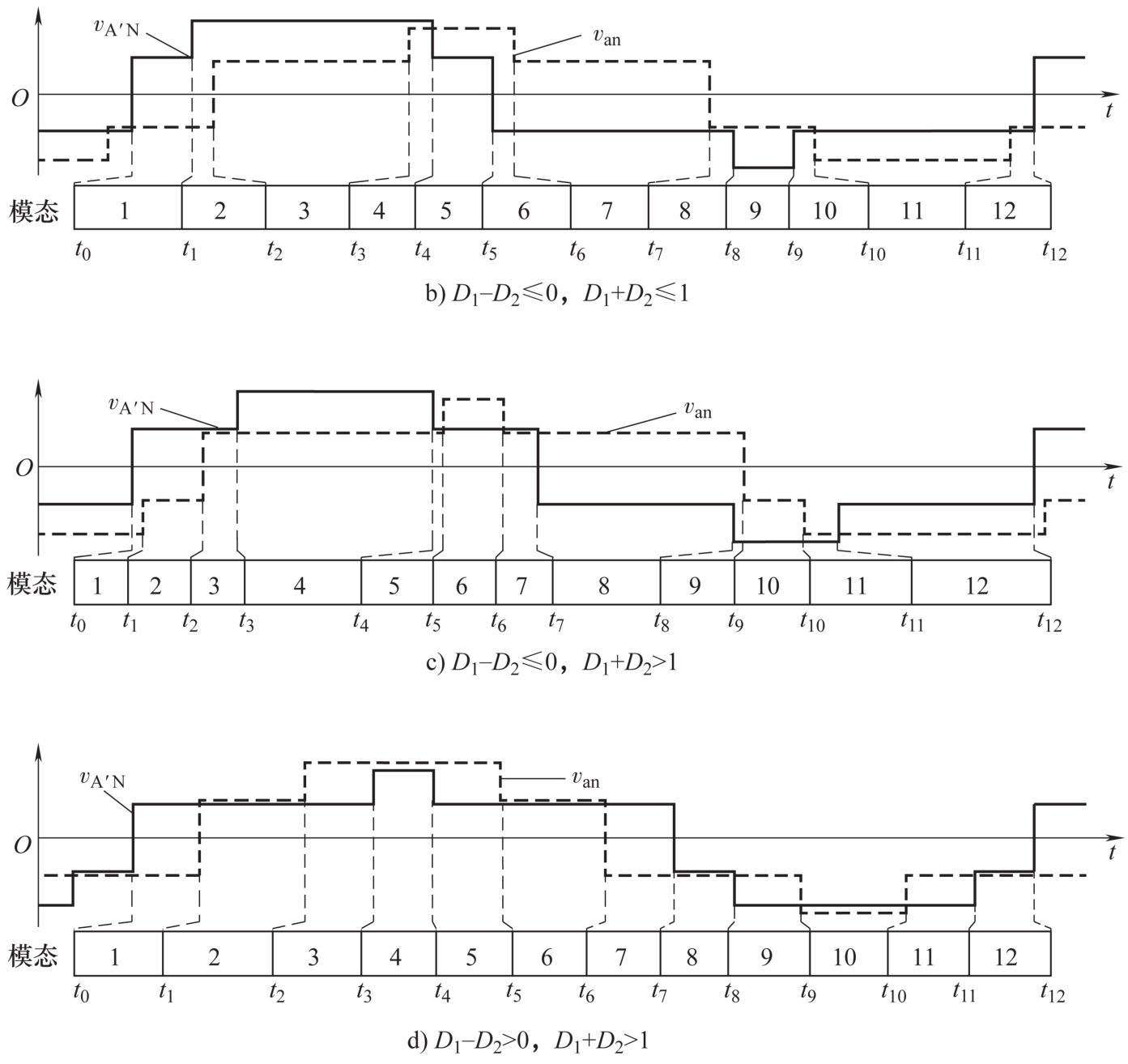
图3.7 不同 D 1 与 D 2 情况下的电压 v A′N 与 v an 波形(续)
其他8种情况中也可按上述方法分为4种类型,其情况分布如图3.8所示,下以其中的情况5a为例分析不同移相占空比 D d 下的工作模态,该情况下, D 1 与 D 2 满足:1/3< D 1 <2/3、1/3< D 2 <2/3、 D 1 -D 2 >0且 D 1 + D 2 ≤1。当移相占空比 D d 由0变化到1时,情况5a又可细分为12种类型,分别如表3.1所示。
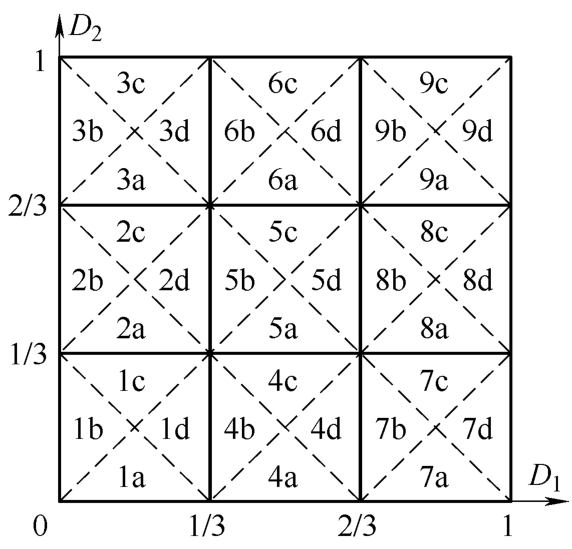
图3.8 不同 D 1 与 D 2 下的工作情况分布
以工作情况5a中的类型1为例(下称作工作情况5a.1),对变换器具体工作模态进行分析,其电压 v A′N 与 v an 如图3.7a所示。该情况可分为12个工作模态,每个模态中电流 i pa 的表达式如表3.2所示。
表3.1 工作情况5a的分类
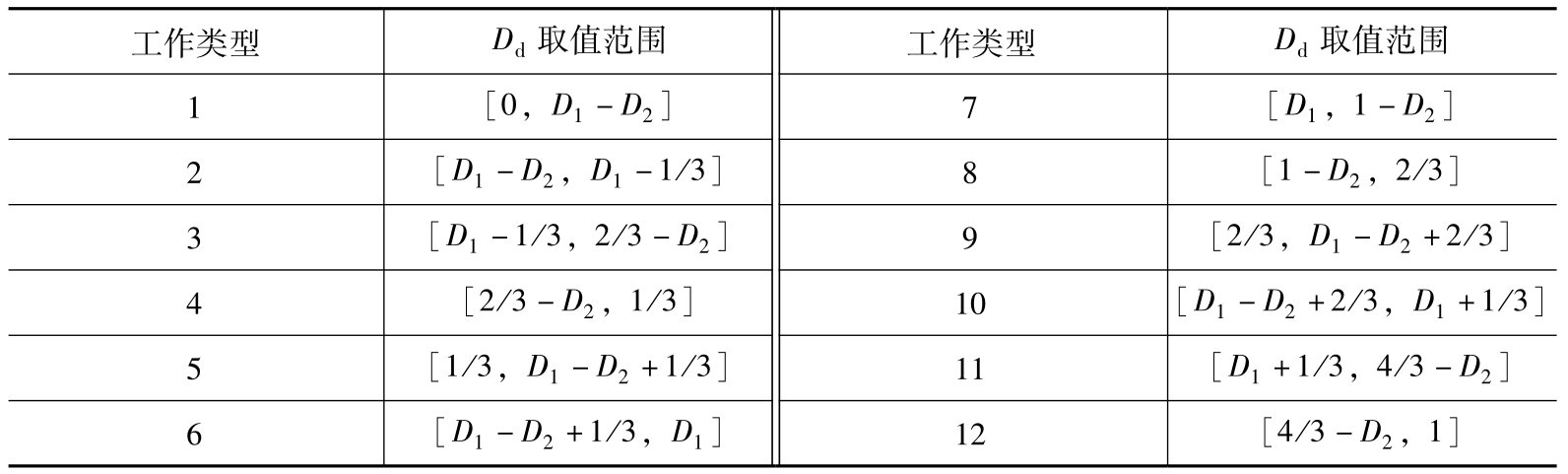
表3.2 工作情况5a.1中电流 i pa 表达式
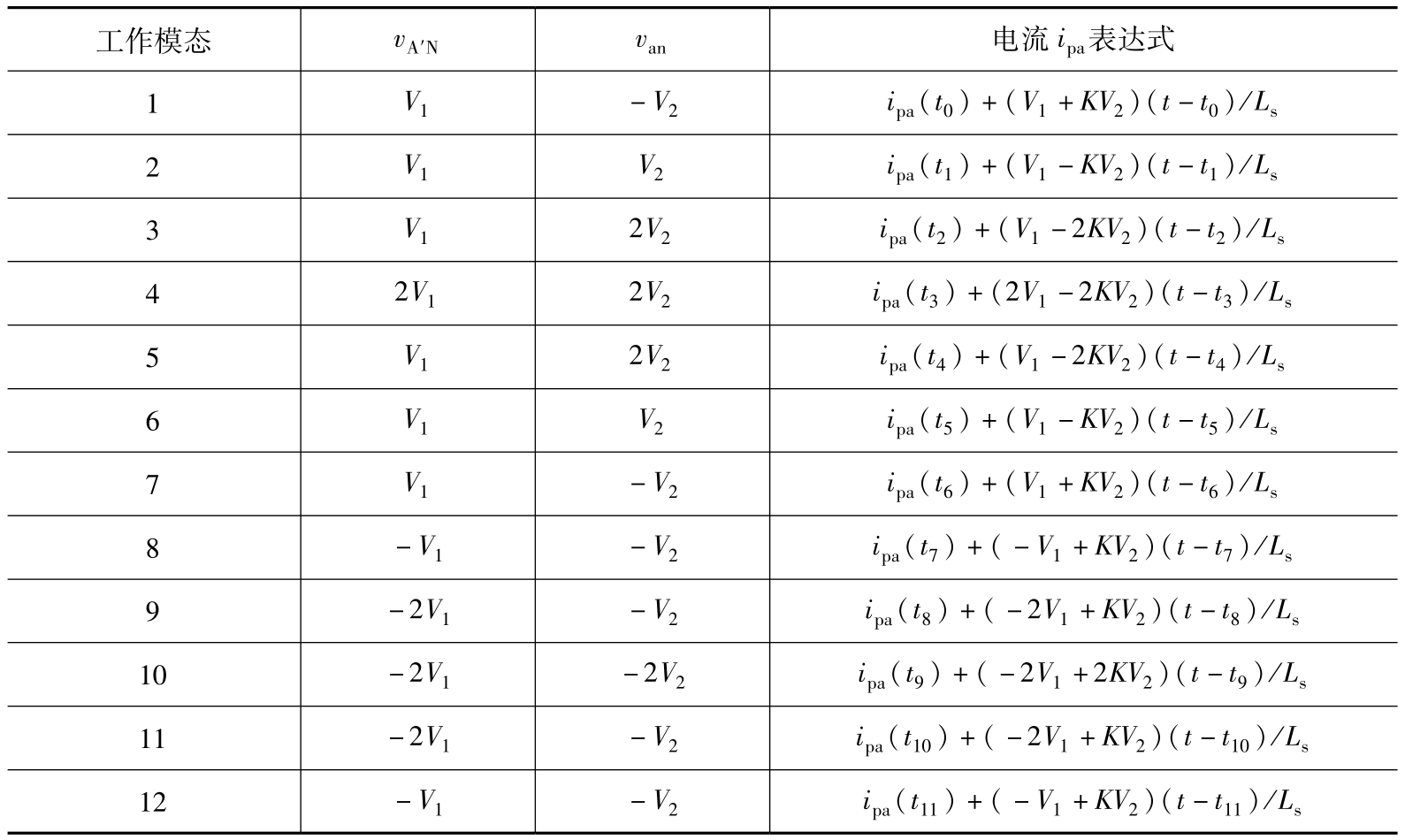
由于三相交错120°工作,电流 i pb 滞后 i pa 以 T s /3,电流 i pc 超前 i pa 以 T s /3,易得电流 i pb 与 i pc 的表达式。根据三相电流 i pa ~ i pc 和等于零,以及三相电流的相位关系,可得式(3.5)。由此可得 t 0 ~ t 12 时刻电流 i pa (t)的值,如表3.3所示,其中, I pa 为 KV 2 T s /(3 L s ); k v 为 V 1 /( KV 2 )。
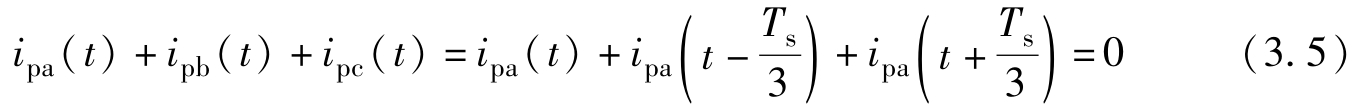
根据表3.2与表3.3,工况5a.1的传输功率 P tot 可以表示为式(3.6)。对于其他工况,可以按相同方法进行建模,得到关键电流与功率表达式,此处不做赘述。
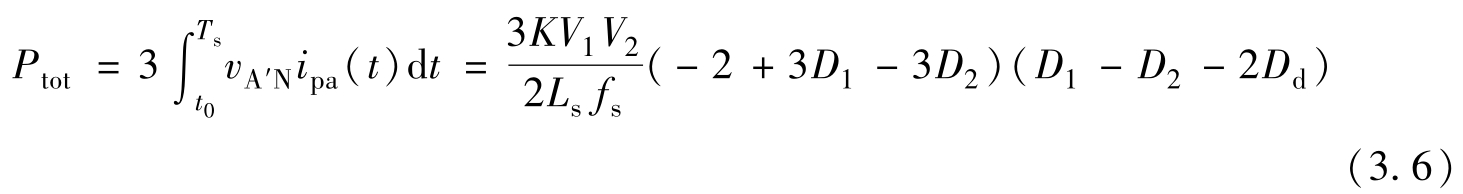
表3.3 工作情况5a.1中各时间节点电流 i pa 值