




城市区域的形态,包括建筑结构、建筑物分布、建筑材料、地表不透水性质和植被覆盖度等,都在不同尺度上深刻地影响着城市边界层过程。这些信息对中尺度数值模式至关重要,直接影响中尺度数值模式的模拟准确度。由美国环境预报中心(NCEP)和美国国家大气研究中心(NCAR)共同研发的WRF模式能够通过陆面模式和城市冠层方案计算出城市区域的各气象要素时空分布,是当前用来模拟城市地区的主流模式。美国早在2009 年便提出了NUDAPT(National Urban Data and Access Portal Tool)计划,该计划旨在为城市冠层方案提供高分辨率城市形态信息,目前已有美国44 个主要城市高分辨率形态参数(Ching et al.,2009;Burian and Ching,2010)。但是目前除美国部分城市外,高分辨率的城市形态参数数据非常匮乏。中国作为最近几十年城市化进程最快的地区,建立中国城市高分辨率城市形态参数数据集对推进中国城市气候研究有着重要的促进作用。然而,有关中国地区城市形态参数的工作开展的较少,类似NUDAPT的全国范围城市形态参数数据集更是空白,因此亟待开展相关的研究。
本数据集所用的基础数据包括中国六十个主要城市的建筑物矢量数据以及全球10 m分辨率地表覆盖数据。建筑物矢量数据提供城市地区建筑物层数、建筑物轮廓数据,地表覆盖数据采用清华大学研发的全球10 m分辨率地表覆盖数据(FROM-GLC10,http:// data. ess.tsinghua. edu. cn/)。目前该数据集分辨率为1 km×1 km(也可以根据需要划分为其他分辨率)。当前WRF城市冠层方案分为两类:单层城市冠层方案(Kusaka et al.,2001)和多层城市冠层方案(Martilli et al.,2009;Salamanca et al.,2010)。本数据集包含常用城市冠层所需参数信息,具体变量参见表3.1.1,三维参数包括Frontal Area Density,Plan Area Density,Roof Area Density以及Distribution of Building Heights,其他参数均为二维参数。本数据集水平分辨率为1 km,垂直分辨率为5 m,垂直方向上共分为15层,最高为75 m(表3.1.1)。
表3.1.1 UCPs参数列表

(续表)
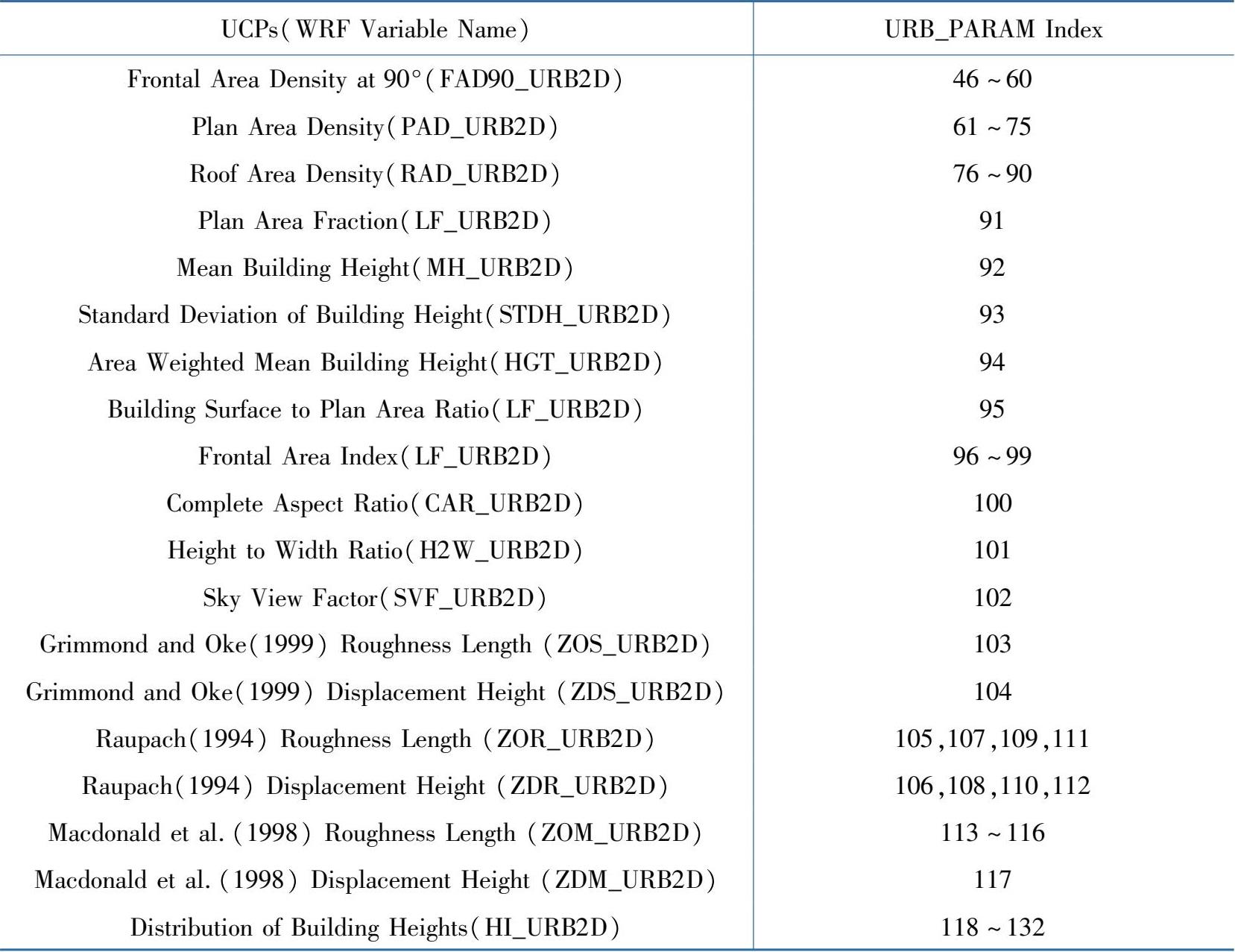
表3.1.1给出了WRF模式中所需要的城市冠层参数,其中参与城市冠层方案计算的主要参数计算方法如下:
网格建筑平均高度及建筑高度标准差计算方法为:
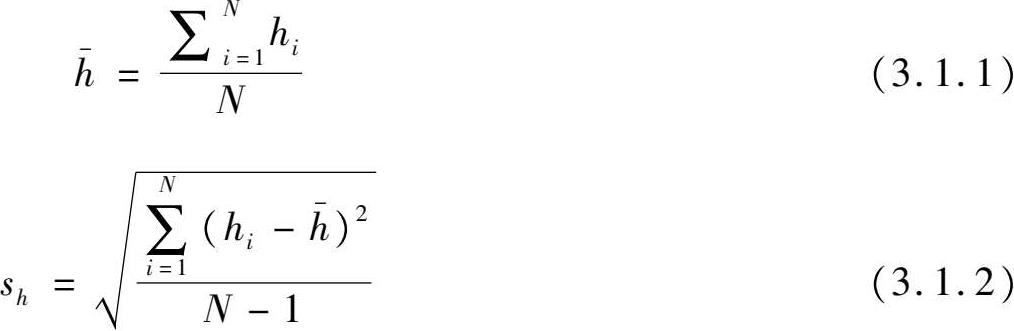
其中h i 代表网格内每栋建筑物高度,N代表网格内建筑物数量。
建筑物水平投影面积比定义为网格内建筑物水平投影面积之和与网格面积之比,计算方法如下:

其中A P 为网格内建筑物水平投影面积之和,A T 为网格面积。
与建筑物水平投影面积比类似,λ b 表示网格内建筑物表面积与网格面积之比,计算公式为:

其中A R 为建筑物水平投影面积,A W 为非水平粗糙元表面积即建筑物墙面面积,A T 为网格面积。
迎风面指数(λ f )定义为特定风向上建筑物投影面积与网格面积之比,并用4 个方向上的迎风面指数代表所有方向上的值,其计算公式如下:

其中4个方向分别为0°,45°,90°和135°,由于建筑物阻挡作用的对称性,这4个方向上的数据可以对应地应用在16个风向上。
中国幅员辽阔,由于地形条件及气候环境等因素的影响,城市人口分布表现出一定的区域特征,地理学上通常用“胡焕庸线”来表现这种差异。“胡焕庸线”即从黑龙江黑河市到云南省腾冲的连线,线东南方国土面积约占40%,居住着超过90%的人口,“胡焕庸线”东南地区城市人口远大于其西北地区。对中国城市形态参数初步分析发现,除了城市人口分布在空间上存在差异外,城市形态在空间上也存在较大的差异性,这种差异可以通过城市形态参数体现出来。中国主要城市高度信息统计量分布情况,由图3.1.1可以看出,中国城市主要分布在“胡焕庸线”东南侧,城市建筑平均高度、中位数高度和高度均方差都呈现出南高北低的格局。城市建筑平均高度和中位数高度可以表征城市建筑物高度总体特征,而建筑高度均方差则代表建筑物高度离散情况,即建筑物高度跨度大小。在60 个城市中,拉萨平均高度、中位数高度和高度均方差都最小,三个统计量分别为6.4,6,2.5 m,表明拉萨建筑物形态较为均一,多为低矮建筑;相反,表征香港高度统计量的数值除高度中位数外均最大(中位数为第二大),分别为23.2,15,24.1 m,表明香港高大建筑物较多,并且建筑物高度跨度较广,低矮建筑和高大建筑都占很大比重。
除了城市建筑物高度统计量信息在空间分布上存在一定的差异性外,其他城市形态参数在空间分布上也有一定的规律性。图3.1.2给出了60个城市建筑水平投影面积比(λ p )、建筑表面积比(λ b )和建筑迎风面指数(λ f )的空间分布情况。西部地区(“胡焕庸线”以西)、海南及东南沿海地区城市建筑水平投影面积比(λ p )大于其他地区,三大城市群中珠三角平均值最大。城市建筑表面积比(λ b )除香港、澳门外,其他城市无明显差异,说明中国城市单位面积上建筑物表面积基本一致,而香港、澳门由于建筑用地紧张,建筑物密集,导致单位面积上建筑表面积较大。对60个城市建筑迎风面指数(λ f )研究发现,中国城市建筑物在4个方向上迎风面指数差异极小,这说明中国城市建筑物形态较为规整,各方向形态一致,故本节用4个方向上平均建筑迎风面指数来表征建筑迎风面特征。除香港、澳门等城市,其他城市建筑迎风面指数差异不大,空间分布较为均匀。
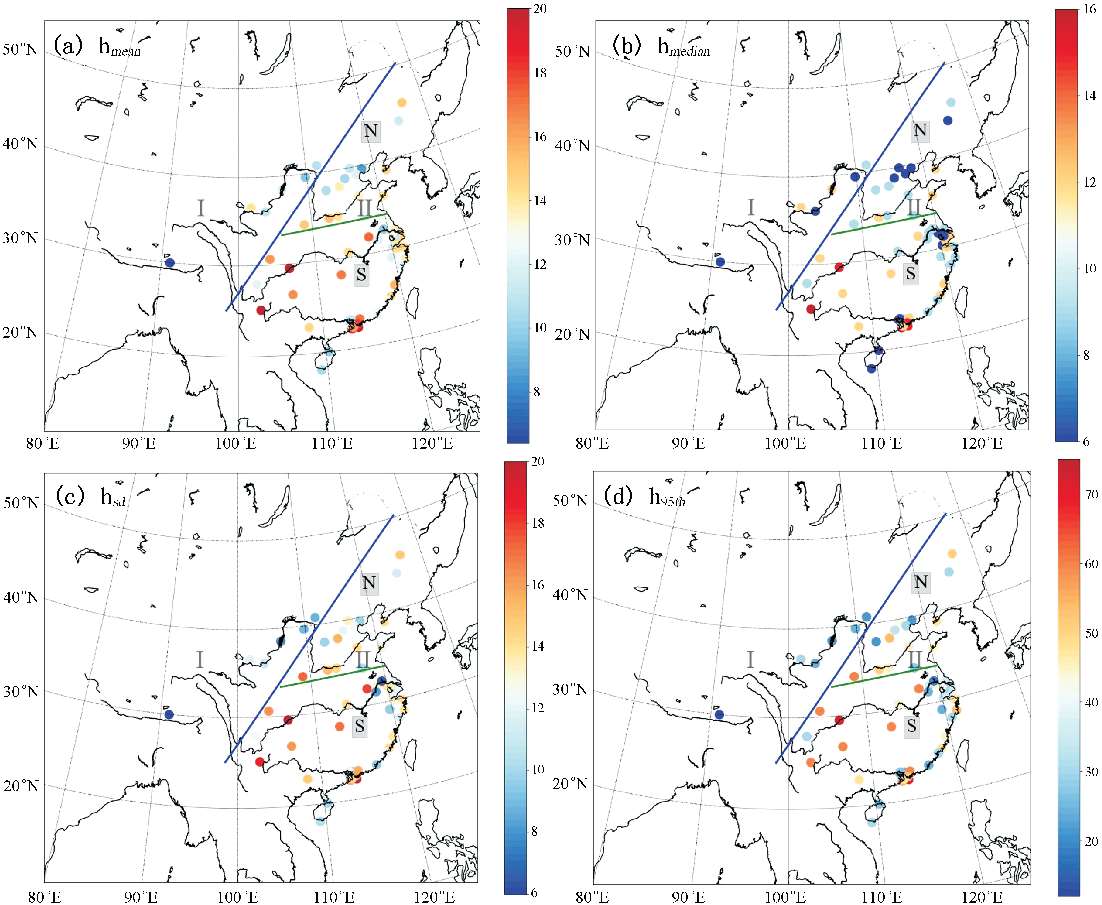
图3.1.1 中国60个城市平均高度、中位数高度、高度均方差、95分位高度空间分布(蓝线为“胡焕庸线”、绿线为秦岭—淮河线,I、II区表示东、西部,S、N表示南、北地区,单位:m)
对各城市建筑物高度分布的分析则表明,中国城市结构形态可以分为两类:单峰结构和双峰结构。图3.1.3给出了两种形态典型的建筑物高度概率密度曲线,由图3.1.3可知,单峰形态城市建筑物高度峰值集中在2层,随后概率随层数减小,高层建筑占比较小;双峰形态城市建筑物高度除了在2层处有一峰值外,在6层处还存在第二个峰值,并且高层建筑占比相对于低层建筑也较小。结合两种城市建筑高度分布形态来看,中国城市建筑物以低层建筑为主,高层建筑占比较少,且城市建筑大部分位于12层以下。根据这种城市建筑高度形态分布,60个城市可分为两类,其中单峰形态城市共有29 个,双峰形态城市共有31 个。图3.1.4 给出了两类城市形态建筑物数量随建筑物层数变化情况,由图3.1.4 可以看出,单双峰形态城市建筑物高度及建筑物数量存在明显差异。单峰形态城市建筑物数量远远大于双峰形态城市,单峰形态城市平均建筑物数量约为10.5万,而双峰形态城市平均建筑物数量约为6.8万,单峰形态城市建筑物数量为双峰形态城市建筑物数量的1.5倍。并且两者差异主要集中在12层以下的建筑占比,对12层以上的建筑占比两者差异不大,也就是说低矮建筑物数量的差异是造成城市有单双峰形态之分的主要原因。
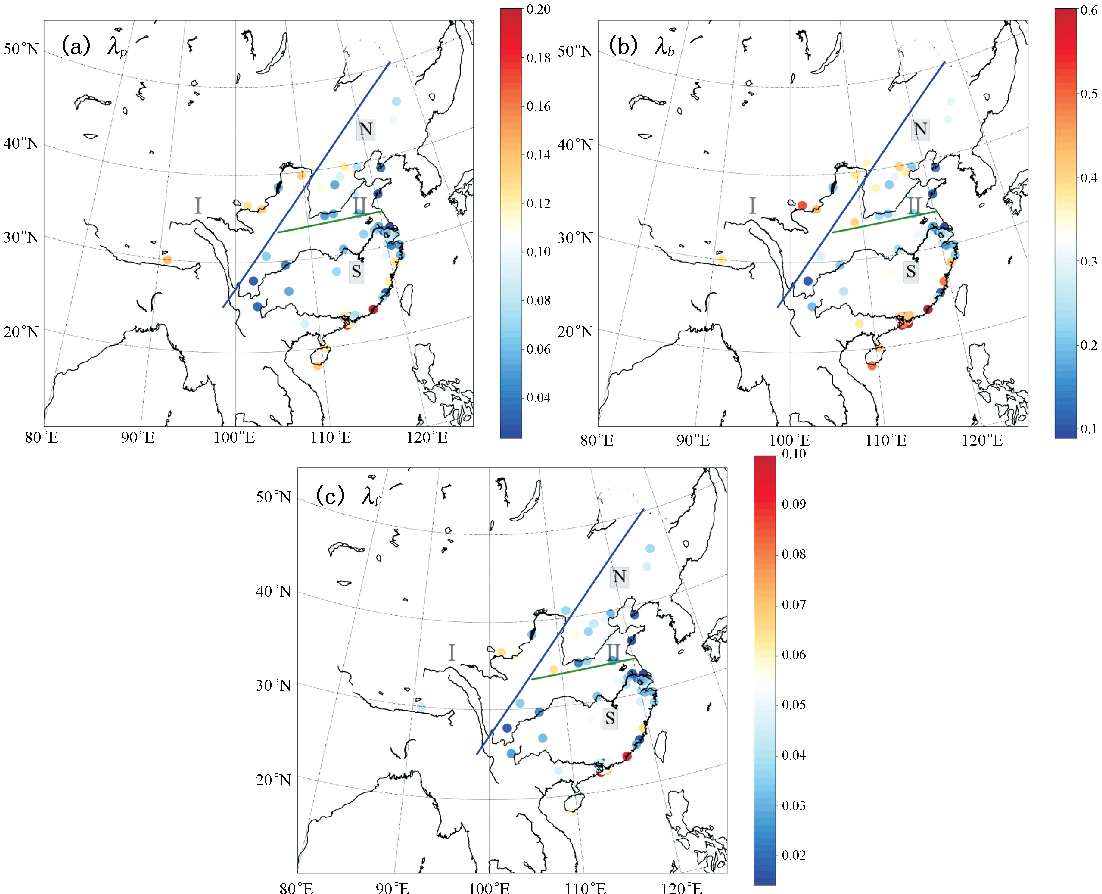
图3.1.2 部分城市形态参数(λ p 、λ b 、λ f )空间分布(蓝线为“胡焕庸线”,绿线为秦岭—淮河线)
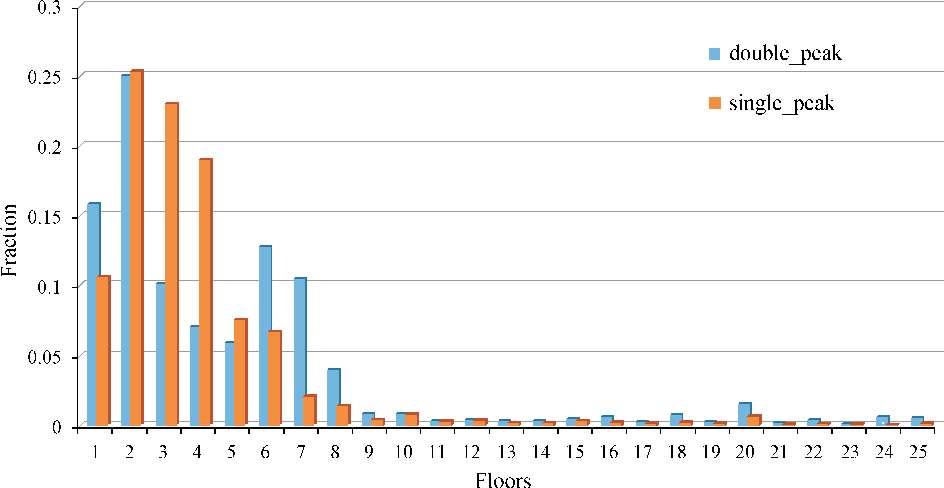
图3.1.3 典型单双峰形态城市建筑物高度概率密度曲线
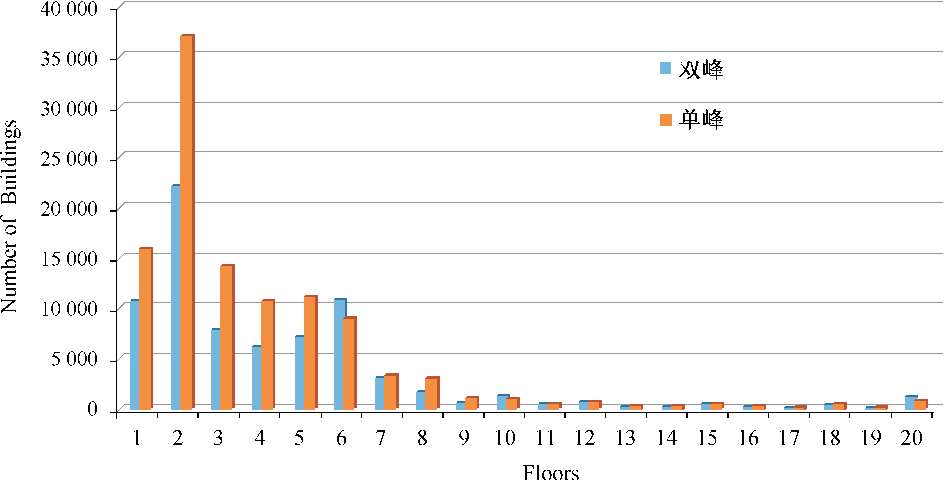
图3.1.4 单双峰形态城市建筑物数量随高度变化统计
图3.1.5给出了60个城市单双峰形态城市空间分布,由图可以看出单双峰形态城市分布具有一定的区域性和不均匀性。总体来看,北方城市形态以双峰为主,南方及东南沿海以单峰为主。从区域分布来看,京津冀和珠三角地区城市以单峰形态为主,长三角地区城市以双峰形态为主,东南沿海城市大多为单峰形态,西南地区则为双峰形态。这种城市形态的差异在城市形态参数上也有较为明显的体现,表3.1.2给出了2种城市结构各城市形态参数对比情况。由表3.1.2可知,单峰形态城市建筑平均高度、中位数高度和水平投影面积加权平均建筑高度都低于双峰形态城市,而单峰形态城市建筑高度均方差大于双峰形态城市。同时,单峰形态城市建筑水平投影面积比(λ p )、建筑表面积比(λ b )和建筑平均迎风面指数(λ f )都要大于双峰城市。
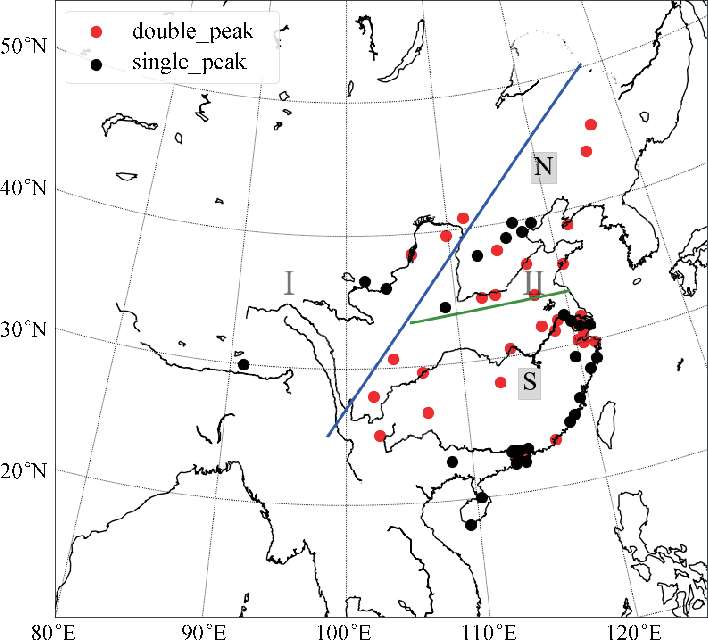
图3.1.5 单双峰形态城市空间分布(红点代表双峰形态城市,黑点代表单峰形态城市,蓝线为“胡焕庸线”,绿线为秦岭—淮河线)
表3.1.2 单双峰结构城市形态参数统计表

WRF模式中不同城市冠层方案对城市建筑物形态做了不同程度的简化,所需要的城市形态参数也不尽相同,为了探究WRF模式对城市冠层参数的敏感性问题,我们对南京的一次晴天过程进行了模拟。本次模拟采用三重嵌套,模拟区域如图3.1.6 所示,模拟时间为2017年8月4日08时—2017年8月8日08时(北京时,下同),其中前24小时为模拟调整时间。模拟区域中心经纬度为118.8 °E和32.06 °N,水平网格距分别为9,3和1 km。本研究共设计了两组实验:采用WRF默认城市形态参数的Default算例,以及采用高分辨率城市形态参数的UCPs算例(表3.1.3),所有算例除城市冠层方案选择不同,其他参数化方案均相同,表3.1.4给出了模式模拟主要参数设置情况。
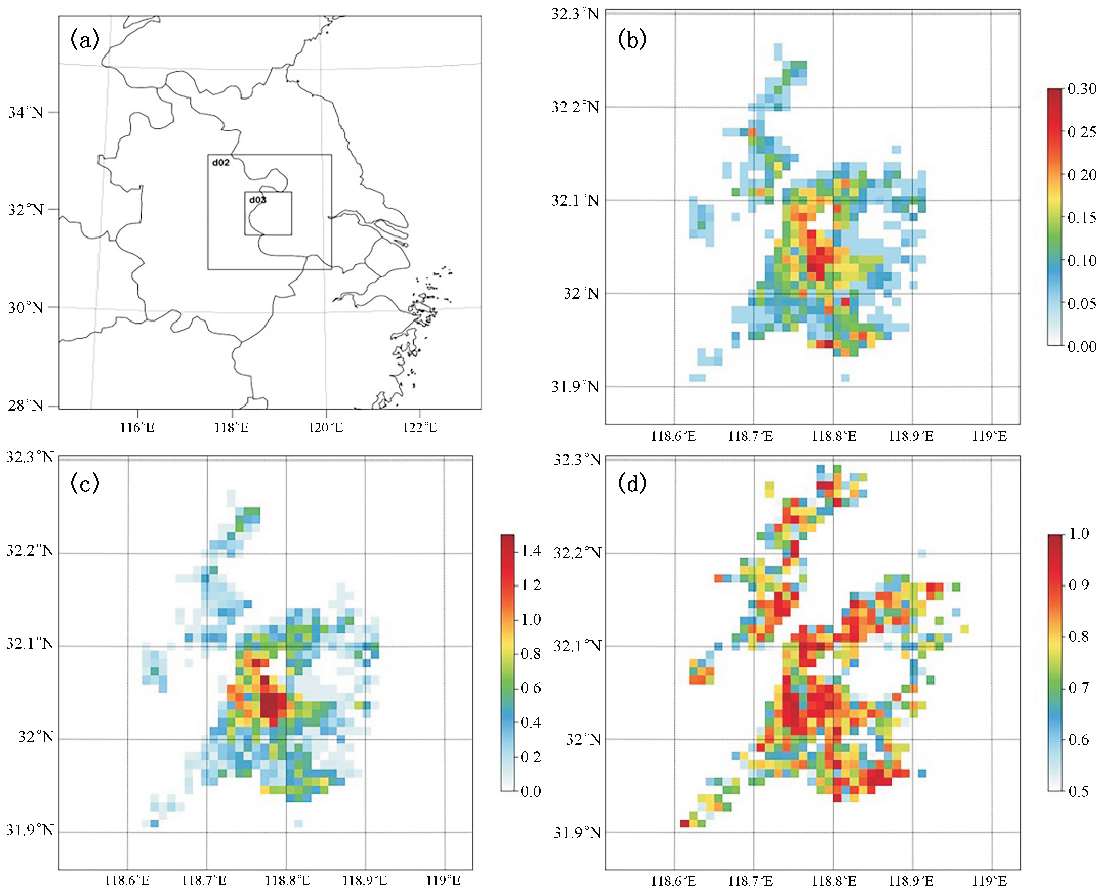
图3.1.6 模拟区域分布及南京部分城市形态参数空间分布
(a)研究区域;(b)建筑平面面积分数;(c)建筑表面积与平面面积之比;(d)不透水表面覆盖率
表3.1.3 Default算例与UCP算例介绍
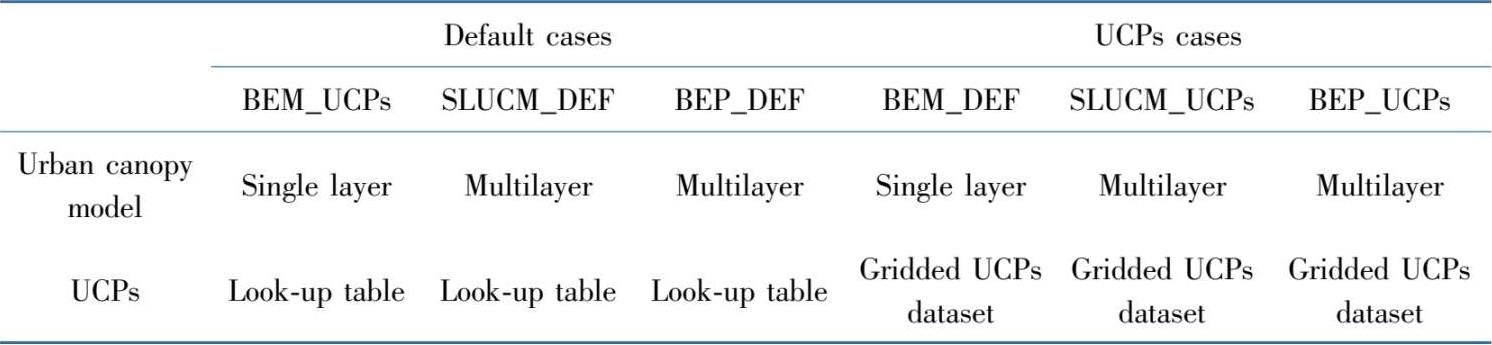
表3.1.4 模式主要模拟参数设置

图3.1.7给出了南京建筑物高度分布概率空间分布。由图3.1.6(b),(c)可以看出λ p 和λ b 分布有较强的一致性,极大值都位于市中心,表明市中心建筑表面积最多,并且由图3.1.7(a),( g )可以认为市中心建筑表面积主要贡献来源于低矮建筑。南京市中心建筑物数量远远大于其他区域,10 m以下建筑物占比超过50%,南京市中心建筑物密度明显高于其他区域。南京20 m以上建筑主要分布在城市外围区域(图3.1.7(d)~(f)),这也就解释了为什么建筑物投影面积加权高度(Haw)在市中心和城市外围区域均有较大数值(图3.1.7(h))。
城市建筑全面积在城市能量平衡过程中有重要影响,城市不透水面覆盖度一定时,单层城市冠层方案建筑全面积主要受建筑平均高度影响,多层城市冠层方案则主要受建筑物高度概率分布影响。WRF单层城市冠层方案(SLUCM)对建筑物高度进行了归一化处理,街渠宽度(街道宽度与建筑宽度之和)为1,街宽、楼宽以及建筑物高度处理为各自占街渠宽度的占比。图3.1.8给出了UCPs算例与Default算例之间建筑表面积差值水平分布,SLUCM用建筑物归一高度之差表示,BEP与BEP+BEM则直接用建筑物全面积之差。为了进一步探究WRF城市冠层方案对城市形态参数的敏感性问题,本节选取UCPs与Default算例建筑表面积差异较大的两个区域,区域1UCPs算例建筑高度与建筑全面积均大于Default算例,区域2则相反。
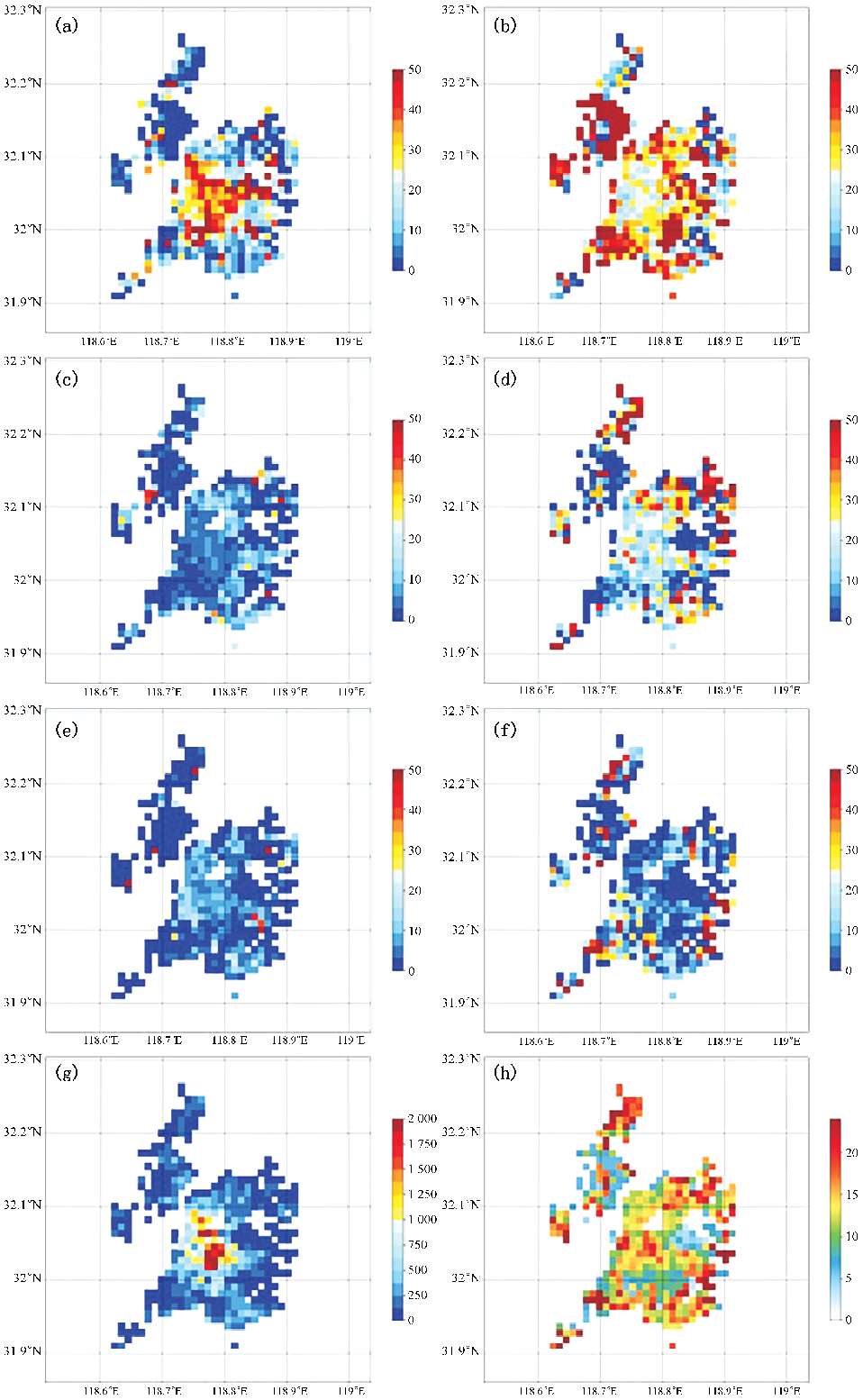
图3.1.7 南京建筑物高度分布概率空间分布
(a-f)高度< 10 m,(10-15]m,(15-20]m,(20-25]m,(25~30]m,> 30 m建筑物个数百分比;(g)建筑物单位空间个数;(h)Haw空间分布(m)
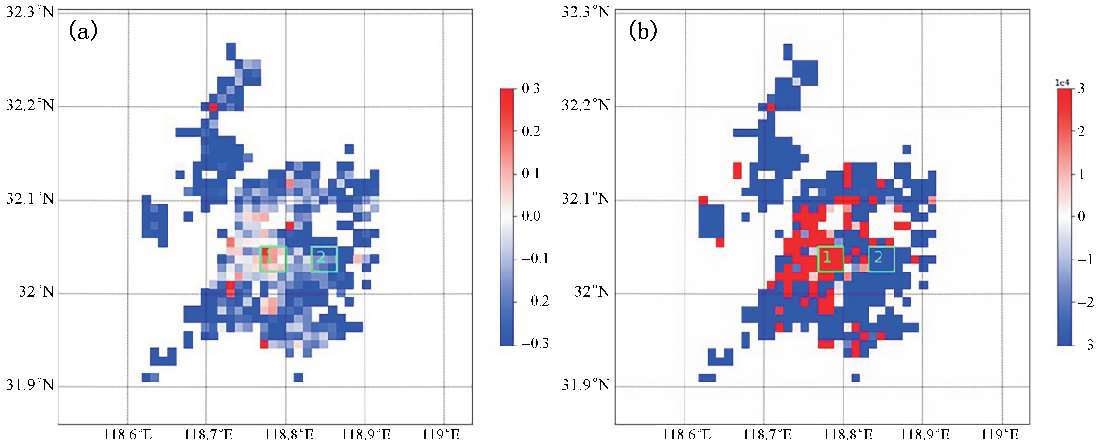
图3.1.8(a)南京平均建筑物归一高度(无量纲量)差值水平分布(UCPs-default);(b)南京建筑全面积差值水平分布(UCPs-default)
图3.1.9给出了2017年7月31日08时—8月1日08时市中心2 m温度和冠层风速日变化情况,由图3.1.9可见,引入城市形态参数后,WRF对2 m温度和冠层风速的模拟效果有显著提升,WRF对城市形态参数较为敏感。城市形态参数对2 m温度的影响主要体现在白天,而对冠层平均风速的影响则是全天。以区域1 为例,default算例模拟出的2 m温度略低于观测值,特别是BEP_DEF和BEM_DEF方案,对2 m温度的低估更多;引入城市形态参数后,三种城市冠层方案对2 m温度的模拟都有提升,基本与观测值相同,其中BEM_UCPs算例2 m温度模拟值与观测值最为接近。这是因为UCPs算例在区域1 建筑表面积要大于default算例,建筑表面吸收更多的太阳辐射,使城市增温,区域2 则相反,致使UCPs算例模拟出更低的2 m温度。从三种方案2 m温度的模拟效果来看,城市形态参数对多层城市冠层方案2 m温度的模拟效果提升要大于单层城市冠层方案,SLUCM温度对UCPs相对不敏感。从冠层风速来看,SLUCM_UCPs算例对风速的模拟与观测值最为接近,并且城市形态参数对单层城市冠层方案风速模拟提升最大,这可能是因为SLUCM_UCPs直接调用了表征城市建筑迎风面积的迎风面指数,对城市风场的模拟影响最为直接,提升了WRF模式对风速的模拟能力。
城市形态对辐射过程的影响主要有三点:辐射截陷、阴影遮蔽和建筑储热,三者存在复杂的竞争关系,总的作用效果与城市具体形态有关。建筑物高度和建筑物密度是决定三者竞争关系的关键因素,同时也是影响城市风场的决定性因素。WRF模式默认参数对城市形态的描述存在偏差,而这些偏差对城市地区辐射过程及动力过程有所影响。引入高分辨率的城市冠层参数后,WRF模式对城市形态的描述更为准确,从而更为合理地进行各个物理过程的计算,尤其是城市区域辐射过程和建筑物对动力过程的影响。总体来说,WRF模式引入高分辨率UCPs后,WRF模式对城市地区模拟效果有所提升,这种提升主要体现在对城市地区风速的模拟和城市温度的模拟上。
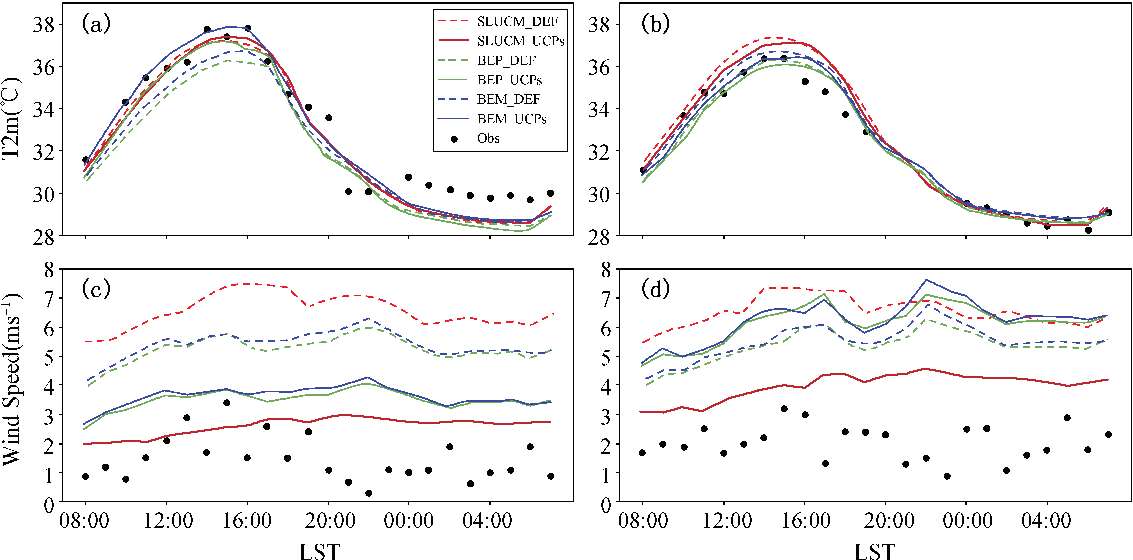
图3.1.9 2017年7月31日08时—2017年8月1日08时平均2 m温度、平均冠层风速日变化曲线(区域1:(a),(c);区域2:(b),(d);观测数据选取各自区域内典型城市站点)