




等离子体的基本行为不仅取决于等离子体与外场的相互作用,也与等离子体质点之间的相互作用有关,本质上是一种集体效应,必须用统计物理学方法来处理。由于数学上的困难,通常在条件许可情况下,往往用近似理论来讨论等离子体问题。本节简述用等离子体单粒子模型所给出的结果。
用等离子体的单粒子模型处理问题时,实际上作了四个假定:①忽略了粒子间的相互作用;②不计带电粒子运动所产生的电磁场,且假定
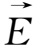 、
、
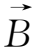 为已知外场;③仅考虑非相对论情形;④忽略带电粒子由于辐射而产生的辐射阻尼。单粒子模型适用于描述稀薄等离子体(对于稀薄等离子体可近似忽略粒子间的相互作用),同时单粒子模型给予我们一种直观的概念,它是我们研究和了解等离子体集体效应的基础。
为已知外场;③仅考虑非相对论情形;④忽略带电粒子由于辐射而产生的辐射阻尼。单粒子模型适用于描述稀薄等离子体(对于稀薄等离子体可近似忽略粒子间的相互作用),同时单粒子模型给予我们一种直观的概念,它是我们研究和了解等离子体集体效应的基础。
在满足以上四个假定的前提下,复杂的运动方程组简化为一个矢量方程:
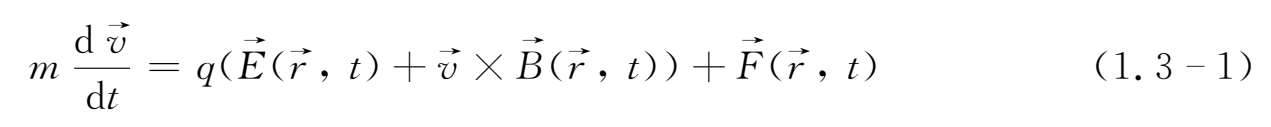
式中
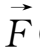 (
(
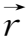 ,t)为除电磁场力以外的外力,其他符号具有通常意义。
,t)为除电磁场力以外的外力,其他符号具有通常意义。
下面将从运动方程(1.3-1)式出发,对
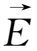 、
、
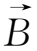 、
、
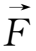 的各种可能情况,由简单到复杂,分别讨论单个带电粒子的运动规律。
的各种可能情况,由简单到复杂,分别讨论单个带电粒子的运动规律。
即在(1.3-1)式中取
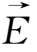 =0,
=0,
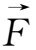 =0,
=0,
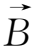 =B
=B
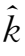 =常矢量。于是运动方程(1.3-1)式具有下列形式:
=常矢量。于是运动方程(1.3-1)式具有下列形式:

其分量形式为
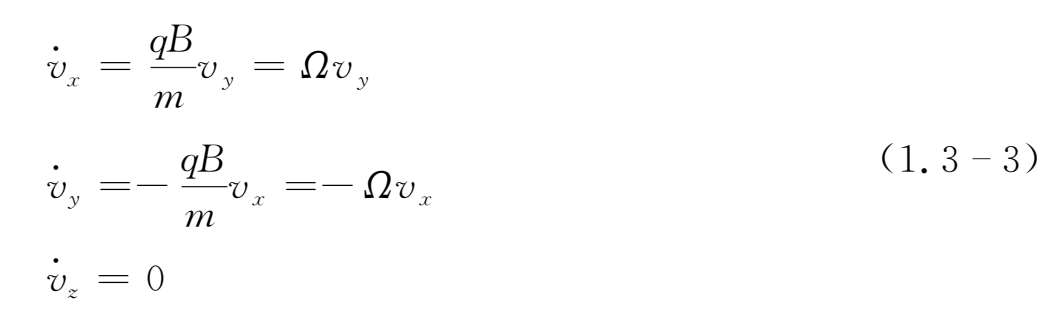
则

式中Ω=
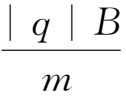 称作拉摩频率或回旋频率。方程(1.3-4)式的解为
称作拉摩频率或回旋频率。方程(1.3-4)式的解为
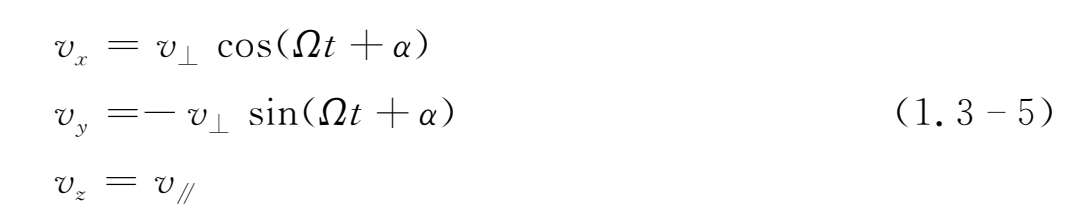
和
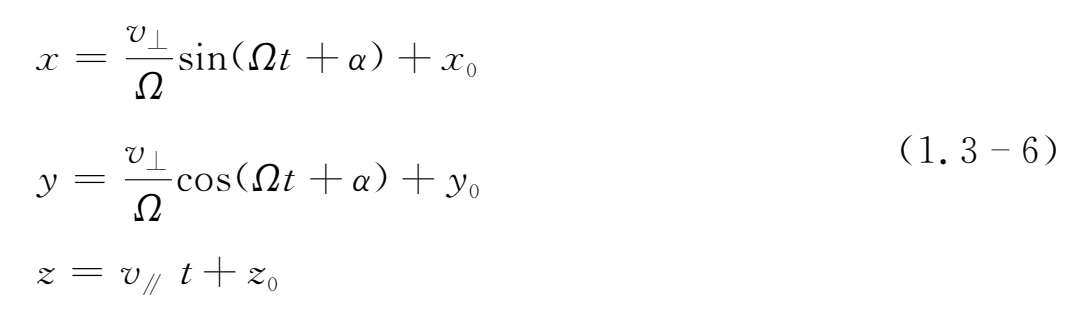
v ⊥ 、v ∥ 、α、x 0 、y 0 、z 0 均为积分常数,由初始条件决定。
解(1.3-5)、(1.3-6)式表明,在均匀稳恒磁场中,粒子沿着
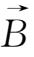 方向做螺旋线运动。粒子在z轴方向(即磁场
方向做螺旋线运动。粒子在z轴方向(即磁场
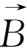 方向)以v∥做匀速运动,而从运动平面z=v
∥
t+z
0
上看,粒子以(x
0
,y
0
)为中心做匀速圆周运动,这两种运动的叠加,便是粒子沿以
方向)以v∥做匀速运动,而从运动平面z=v
∥
t+z
0
上看,粒子以(x
0
,y
0
)为中心做匀速圆周运动,这两种运动的叠加,便是粒子沿以
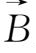 为轴的螺旋线运动。
为轴的螺旋线运动。
必须指出,粒子圆周运动的圆心轨迹为(x
0
,y
0
,z
0
+v
∥
t),它是粒子的瞬时回旋中心,通常我们把这个动点称作引导中心或回旋中心。显然引导中心是粒子运动的平均位置,它的运动方向标志粒子的平均运动方向。拉摩频率Ω=
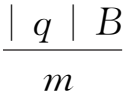 表示粒子在磁场中做圆周运动的圆频率,B越强,Ω越大,粒子回旋越快,回旋一周所需的时间(即周期)就越短。拉摩半径
表示粒子在磁场中做圆周运动的圆频率,B越强,Ω越大,粒子回旋越快,回旋一周所需的时间(即周期)就越短。拉摩半径
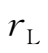 =
=
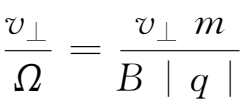 ,与
,与
 成正比,与B成反比。回旋方向是这样选取的:使带电粒子产生的磁场和外加场相反,亦即等离子体粒子的运动倾向于减小磁场,等离子体是抗磁性的。由(1.3-5)式可知,对于正负带电粒子,其回旋运动的方向正好相反(如图 1.3 所示)。一般来讲,正、负带电粒子在空间的轨道是回旋方向相反、回旋半径和回旋频率不等的螺旋线。
成正比,与B成反比。回旋方向是这样选取的:使带电粒子产生的磁场和外加场相反,亦即等离子体粒子的运动倾向于减小磁场,等离子体是抗磁性的。由(1.3-5)式可知,对于正负带电粒子,其回旋运动的方向正好相反(如图 1.3 所示)。一般来讲,正、负带电粒子在空间的轨道是回旋方向相反、回旋半径和回旋频率不等的螺旋线。
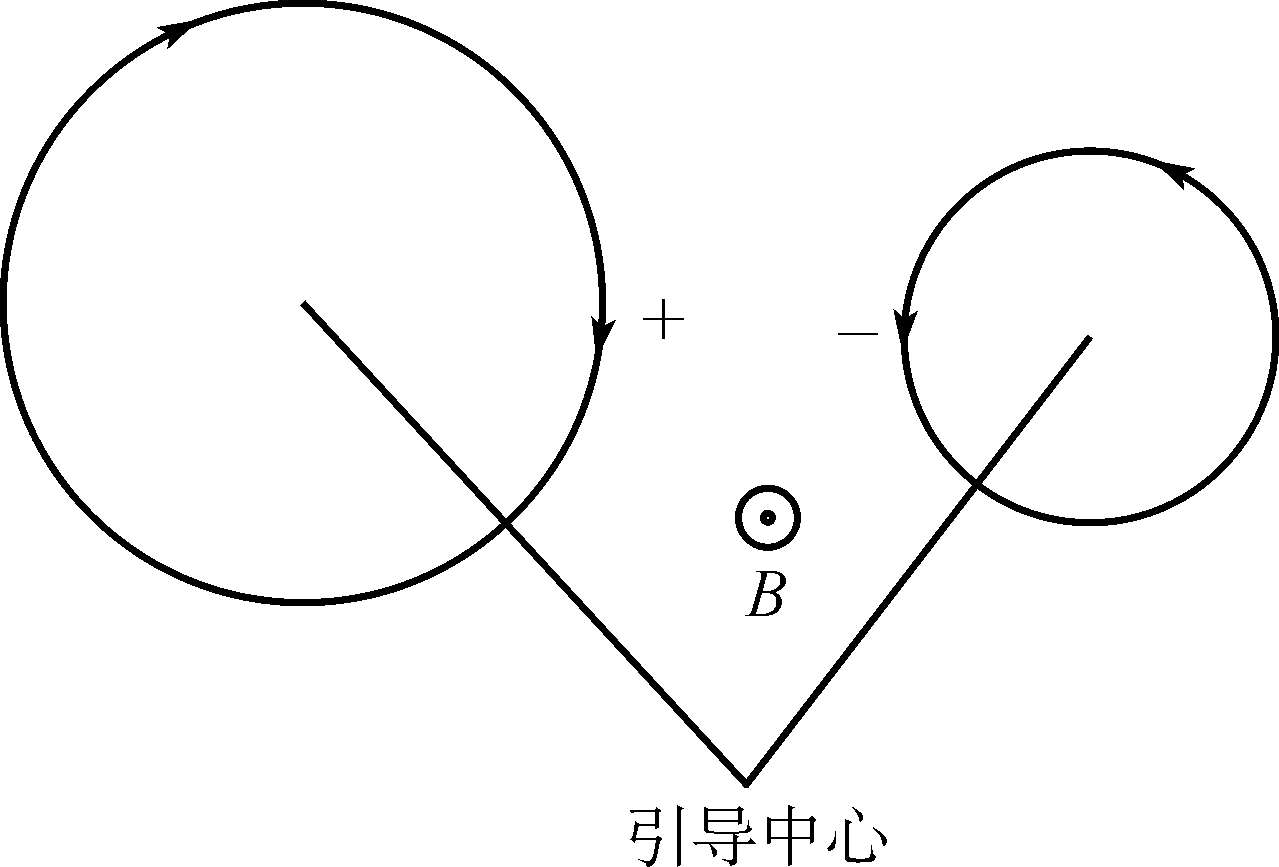
图1.3 带电粒子在均匀稳恒磁场中的回旋运动
对均匀稳恒电磁场,运动方程(1.3-1)式中
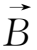 =
=
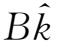 =常矢量,
=常矢量,
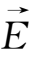 =常矢量,
=常矢量,
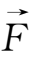 =0。方程(1.3-1)式便成为
=0。方程(1.3-1)式便成为

选择
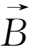 的方向为z轴方向,
的方向为z轴方向,
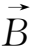 和
和
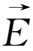 决定的平面为x-z平面,于是
决定的平面为x-z平面,于是
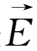 可分解为
可分解为

(1.3-7)式的z分量为

或

这是沿
 方向的简单的加速运动。方程(1.3-7)的横向分量为
方向的简单的加速运动。方程(1.3-7)的横向分量为
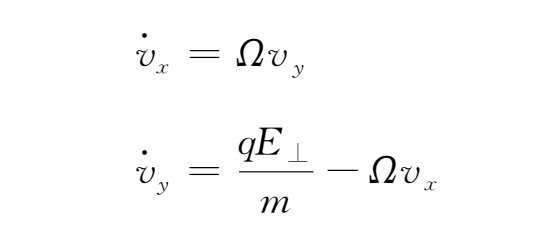
则
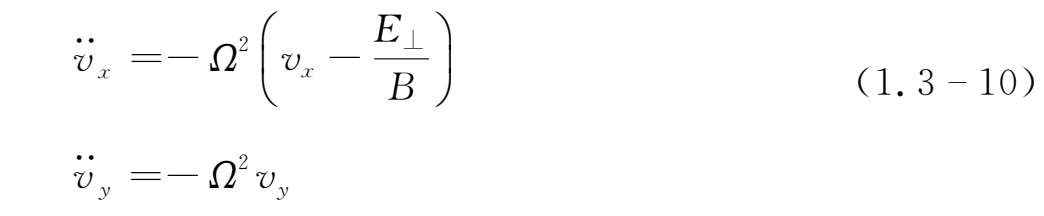
如果用
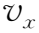 代替(1.3-10)中的
代替(1.3-10)中的
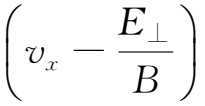 ,则(1.3-10)式简化成(1.3-4)式,因此(1.3-10)式的解为
,则(1.3-10)式简化成(1.3-4)式,因此(1.3-10)式的解为
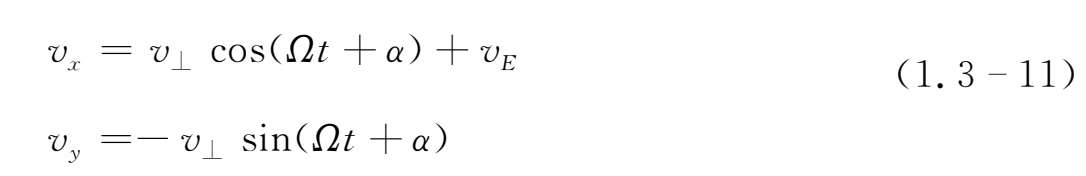
上式为v ⊥ ,v ∥ ,α均为由初始条件决定的常数,而v E 为

比较(1.3-12)与(1.3-5)式,其主要不同点在于垂直于磁场的y方向稳恒电场的存在导致沿x轴方向增加了一个速度v
E
,于是粒子的运动情况与不存在电场时完全不同(如图1.4所示)。此时引导中心的速度
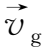 =(v
E
,0,v
∥
),亦即垂直于磁场
=(v
E
,0,v
∥
),亦即垂直于磁场
 的电场的存在,使粒子产生了垂直于电场和磁场方向上的运动,这种运动称为漂移运动。漂移运动的速度v
E
即(1.3-12)式写成矢量形式为
的电场的存在,使粒子产生了垂直于电场和磁场方向上的运动,这种运动称为漂移运动。漂移运动的速度v
E
即(1.3-12)式写成矢量形式为
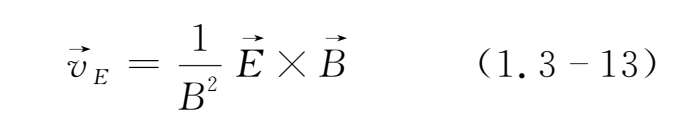
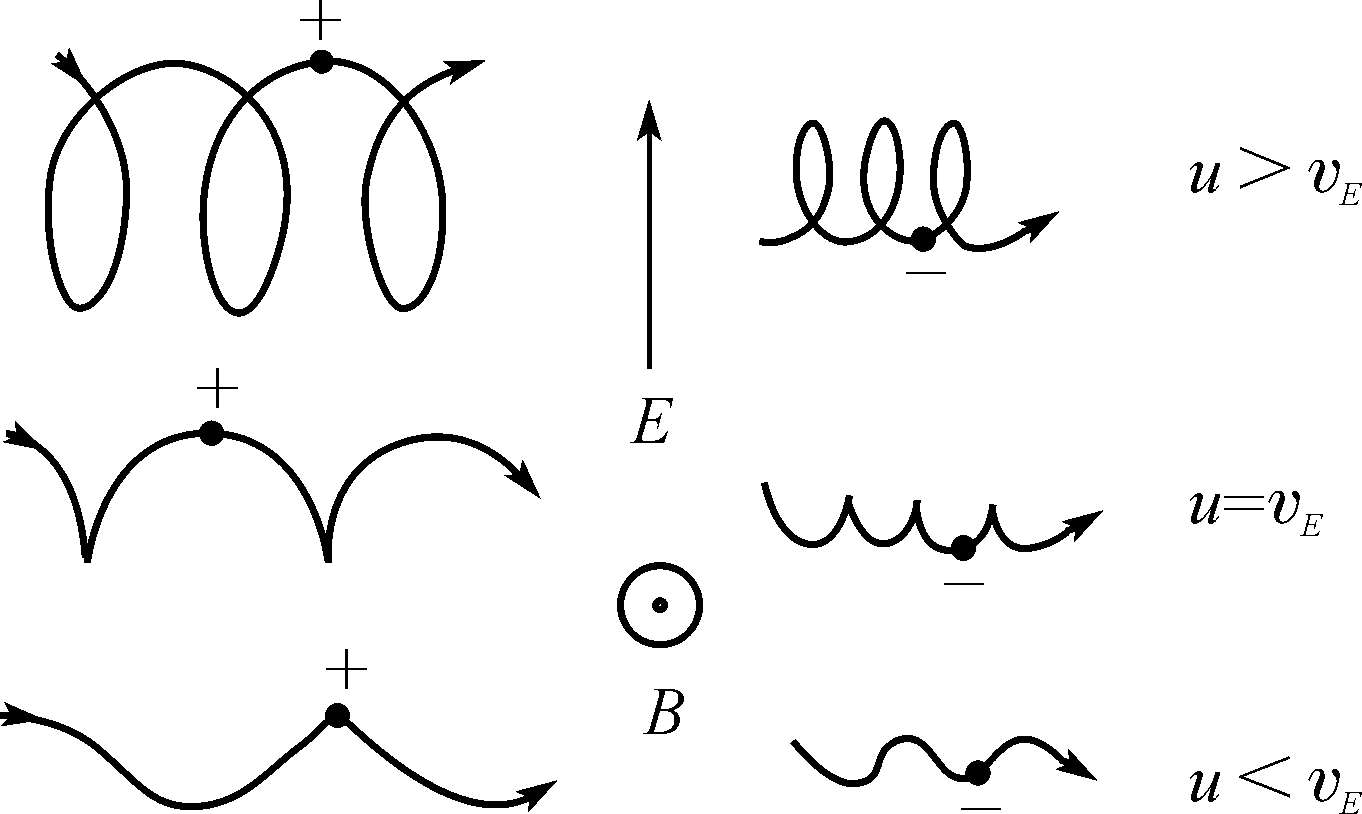
图1.4 均匀稳恒电场产生的漂移
必须指出,对均匀稳恒电场,E ∥ =0,否则与单粒子模型的非相对论性假设相违背,所以此时E ⊥ =E。因此空间中的三维轨道为螺距变化的斜螺旋线(图1.5所示)。
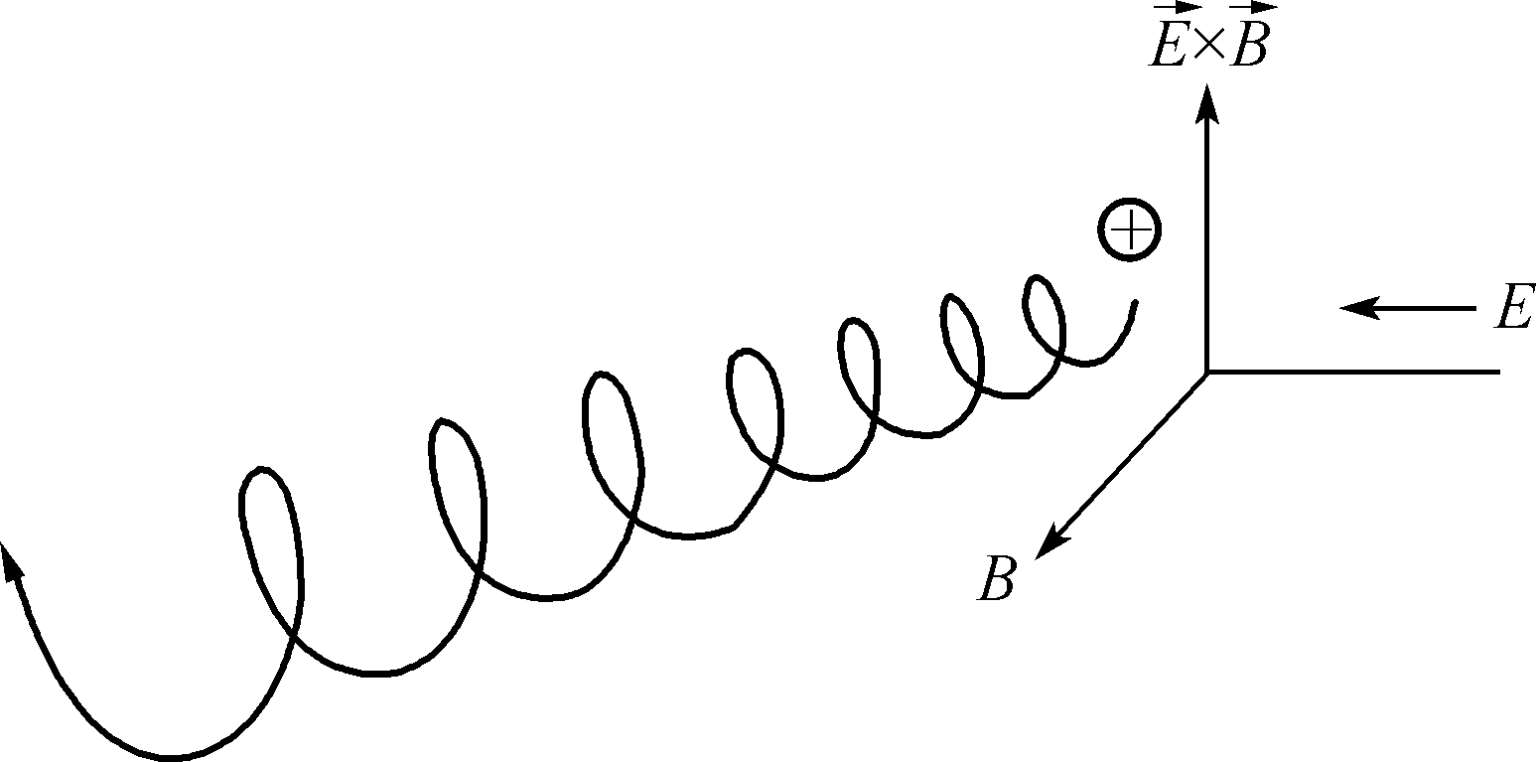
图1.5 均匀稳恒电磁场中带电粒子的实际轨道
推广到一般情况,当带电粒子在均匀恒定磁场中运动时,附加受到由微扰引起的力场或等效力场的作用,使带电粒子的引导中心沿垂直于磁场方向的运动,称为粒子的漂移运动。显然,磁场的存在是粒子漂移的基本条件,而运动方向与磁场方向垂直是漂移运动的基本特征。
下面推导漂移运动速度的一般公式。将附加的等效力场
 分解为沿磁场方向和垂直于磁场方向的两个部分。沿磁场方向的分力
分解为沿磁场方向和垂直于磁场方向的两个部分。沿磁场方向的分力
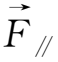 仅使粒子产生一个沿磁力线方向的匀加速度:
仅使粒子产生一个沿磁力线方向的匀加速度:

下面主要讨论垂直于磁场的横向分力
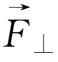 所带来的影响。横向方程为
所带来的影响。横向方程为
我们总可将矢量
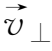 看作两个矢量的合成:
看作两个矢量的合成:

其中
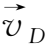 假设是常量。于是(1.3-15)式可改写为
假设是常量。于是(1.3-15)式可改写为
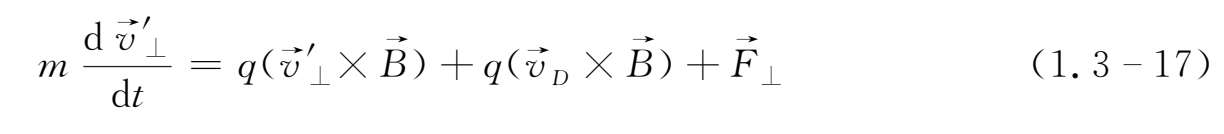
总可适当选择
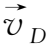 ,使q(
,使q(
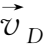 ×
×
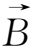 )与附加等效力场的
)与附加等效力场的
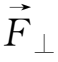 相消:
相消:

那么(1.3-17)式即为

(1.3-19)与(1.3-2)式相似,它同样描述带电粒子以大小不变的横向速度
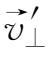 做回旋运动,不同之处仅在于这里是从以速度
做回旋运动,不同之处仅在于这里是从以速度
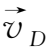 运动的坐标系中观察得到的结果。所以相对于固定坐标系而言,带电粒子还有一个以大小和方向都不变的速度
运动的坐标系中观察得到的结果。所以相对于固定坐标系而言,带电粒子还有一个以大小和方向都不变的速度
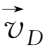 进行的垂直于磁场的漂移运动,漂移速度可由(1.3-18)式确定。将(1.3-18)式两边叉乘
进行的垂直于磁场的漂移运动,漂移速度可由(1.3-18)式确定。将(1.3-18)式两边叉乘
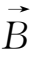 ,考虑到
,考虑到
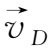 ⊥
⊥
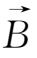 ,又
,又
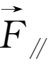 ∥
∥
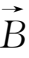 ,因此漂移速度为
,因此漂移速度为

其中
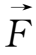 为单位体积的等效力。
为单位体积的等效力。
(1)当等效力场是稳恒电场时,
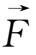 =
=
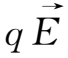 ,由(1.3-20)式所得电漂移速度
,由(1.3-20)式所得电漂移速度
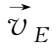 为
为

与(1.3-13)式相同。
(2)如果附加力场是重力
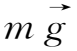 ,则
,则
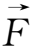 =
=
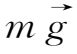 ,由(1.3-20)式可得重力漂移速度
,由(1.3-20)式可得重力漂移速度
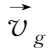 为
为

带电粒子在重力场中的漂移如图1.6所示。
(3)在空间非均匀的磁场中粒子的漂移速度
①当
 ⊥
B ⊥
⊥
B ⊥
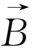 即梯度B漂移
即梯度B漂移
考虑磁力线是直的,但其密度是增加的,例如在y方向增加(如图1.7),即
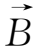 (0,0,B(y))则此时由
(0,0,B(y))则此时由
 ⊥
B产生的等效力为
⊥
B产生的等效力为
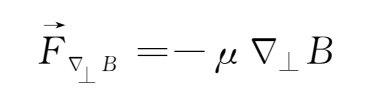
其中μ=
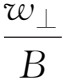 ,
,
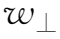 =
=
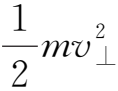 为粒子在垂直于磁场方向上的动能。所以,由于横向磁场梯度的存在所导致的引导中心的漂移速度
为粒子在垂直于磁场方向上的动能。所以,由于横向磁场梯度的存在所导致的引导中心的漂移速度
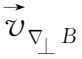 为
为
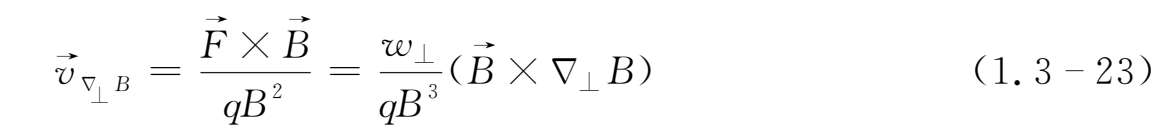
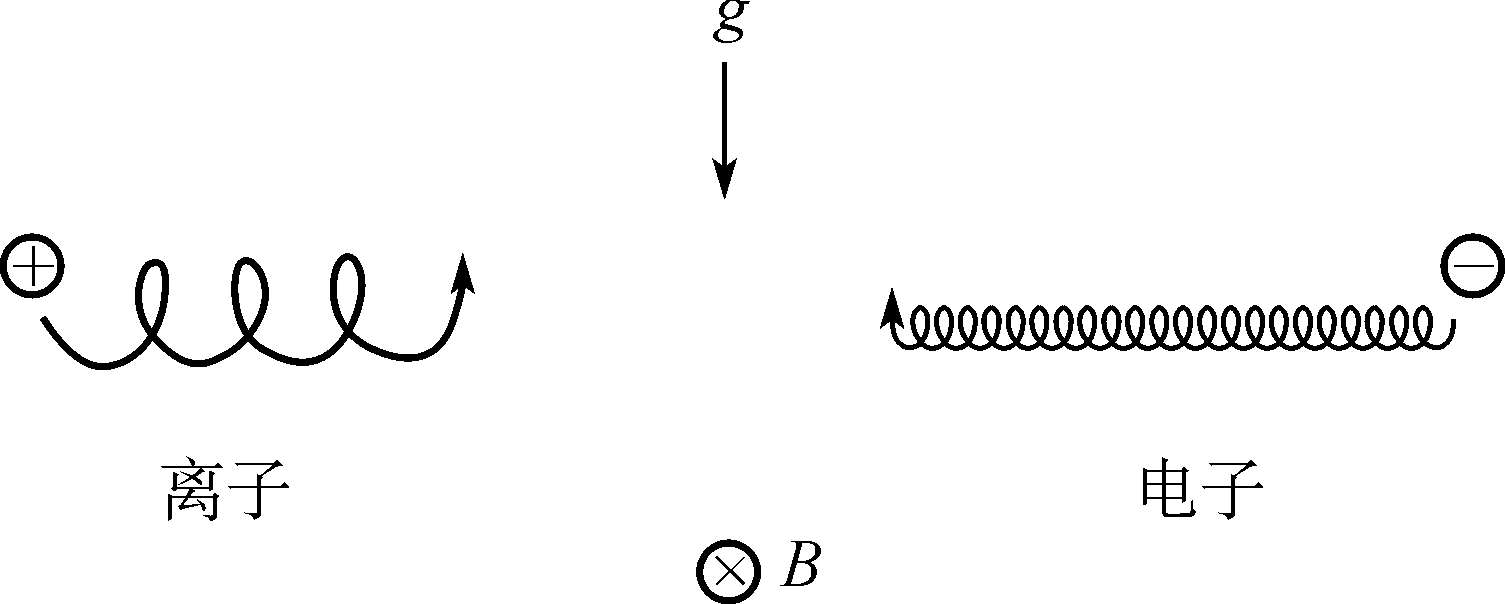
图1.6 重力漂移示意图
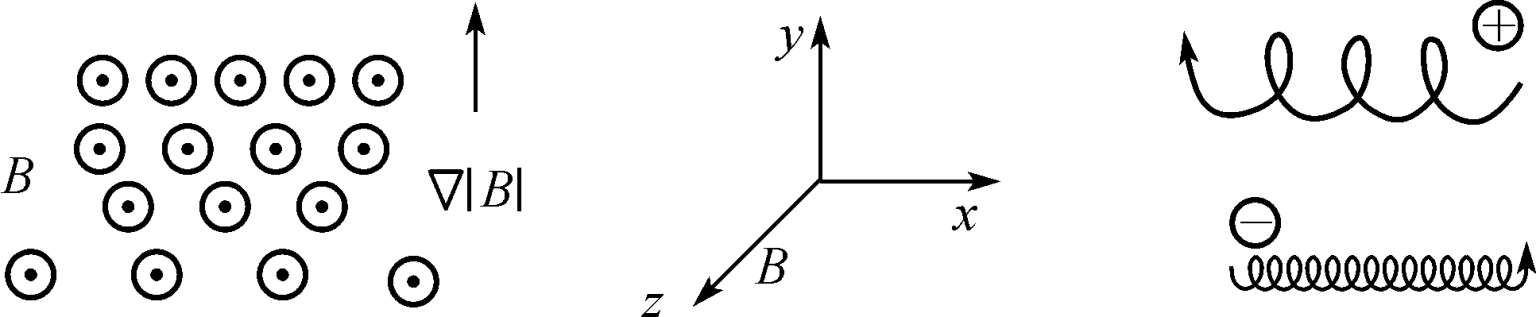
图1.7 梯度漂移示意图
②弯曲
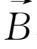 场即曲率漂移
场即曲率漂移
若磁力线的弯曲是微小的并发生在y -z平面中(如图1.8所示),即
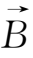 (0,B
y
(z),B)
(0,B
y
(z),B)
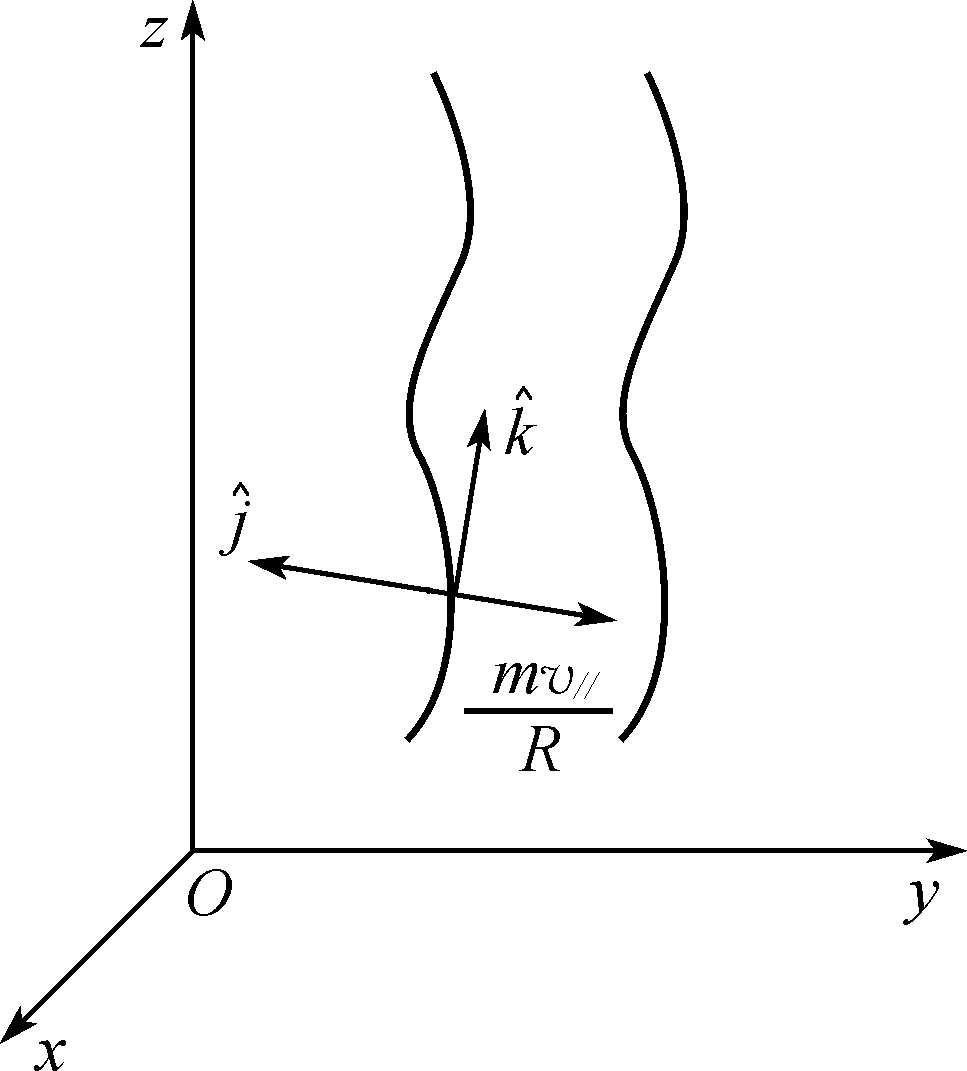
图1.8 曲率漂移示意图
且
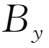 及
及
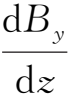 均为小量,即|
均为小量,即|
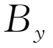 |≪|B|,
|≪|B|,
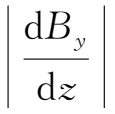 ≪|B|,此时,带电粒子在弯曲磁场中的运动仍可看成是绕一个动点的回旋,不过这个动点现在以v
∥
的速度沿弯曲的磁力线运动着。考虑随引导中心一起运动的局部直角坐标系(单位矢量为
≪|B|,此时,带电粒子在弯曲磁场中的运动仍可看成是绕一个动点的回旋,不过这个动点现在以v
∥
的速度沿弯曲的磁力线运动着。考虑随引导中心一起运动的局部直角坐标系(单位矢量为
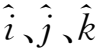 ),坐标轴方向z轴和y轴分别为该点磁力线的切向和主法线方向,则引导中心在运动坐标系中受到的等效力——惯性离心力
),坐标轴方向z轴和y轴分别为该点磁力线的切向和主法线方向,则引导中心在运动坐标系中受到的等效力——惯性离心力
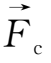 为
为

其中R为曲率半径,R=
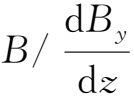 ,代入上式,可得
,代入上式,可得
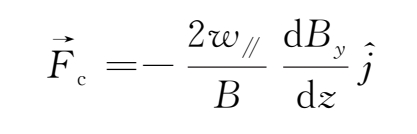
所以由于磁场曲率所导致的曲率漂移速度为
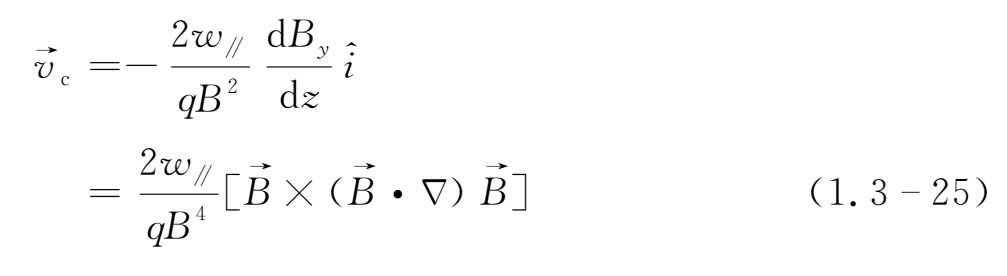
其中
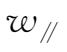 =
=
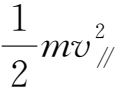 为粒子平行于磁场方向上的动能。
为粒子平行于磁场方向上的动能。
如果磁场的横向不均匀性与纵向不均匀性同时存在,则粒子将同时发生梯度漂移和曲率漂移。若所研究的点不存在电流,即
 ×
×
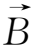 =0,则由梯度漂移和曲率漂移所引起的总漂移速度
=0,则由梯度漂移和曲率漂移所引起的总漂移速度
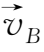 为
为
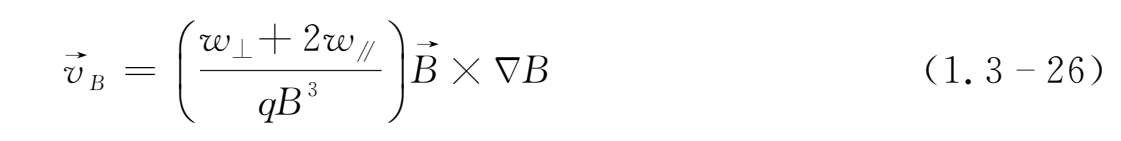
(4)粒子在非稳恒磁场中的运动
设磁场随时间的变化是缓慢的,缓慢变化满足下述条件
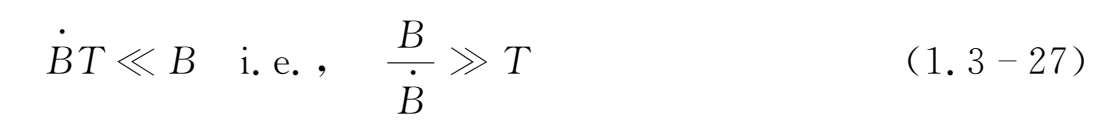
即在一个拉摩周期中,磁场的变化非常小。
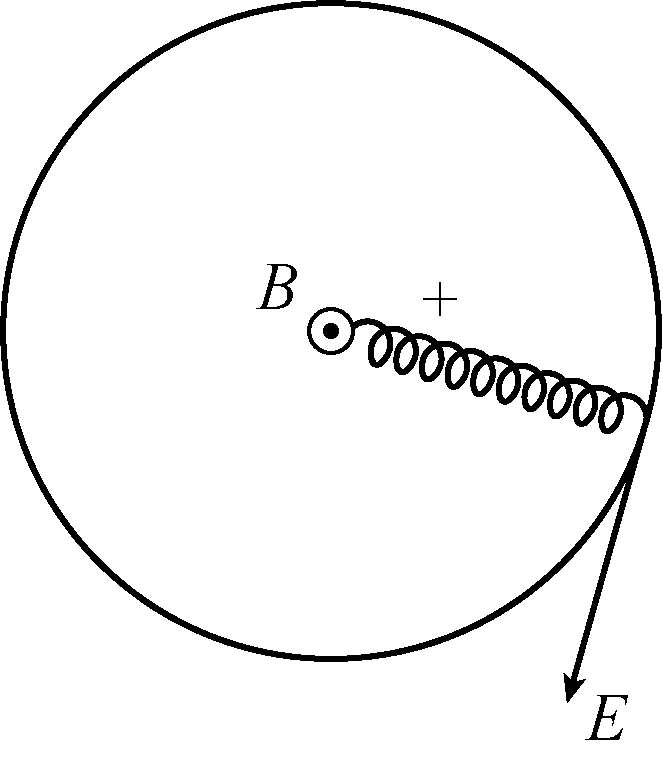
图1.9 随时间变化的磁场中带电粒子的漂移
由电磁感应定律,随时间变化的磁场感应出环向电场(如图1.9所示)。环向电场
 与磁场
与磁场
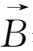 垂直,它将引起带电粒子沿半径方向的漂移运动。即
垂直,它将引起带电粒子沿半径方向的漂移运动。即
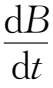 感应产生的环向电场
感应产生的环向电场
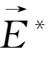 =-
=-
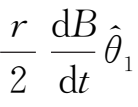 ,其所生成的等效力为
,其所生成的等效力为
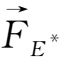 =
=
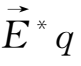 =-
=-
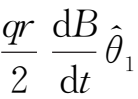 ,故粒子在互相正交的(轴向)磁场与感应的(角向)电场中的漂移速度为
,故粒子在互相正交的(轴向)磁场与感应的(角向)电场中的漂移速度为
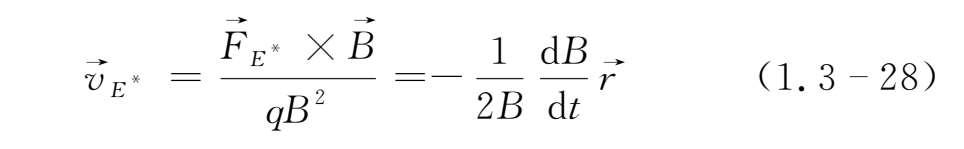
由(1.3-28)式可知,当
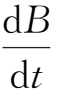 >0,即磁场随时间增大时,粒子沿径向向圆心漂移;而当
>0,即磁场随时间增大时,粒子沿径向向圆心漂移;而当
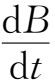 <0 ,即磁场随时间减小时,粒子便离开圆心向外漂移;当磁场变化停止时,径向漂移也就停止。
<0 ,即磁场随时间减小时,粒子便离开圆心向外漂移;当磁场变化停止时,径向漂移也就停止。
综上所述,引导中心漂移的概述如下。
一般公式:

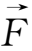 为电场力:
为电场力:

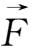 为由非稳恒磁场产生的等效电场力:
为由非稳恒磁场产生的等效电场力:
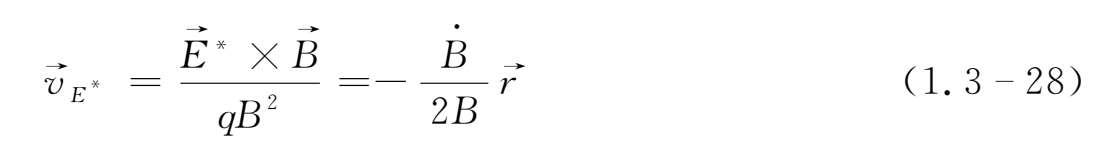
 为重力场:
为重力场:

 为非均匀磁场:
为非均匀磁场:
梯度漂移:

曲率漂移:
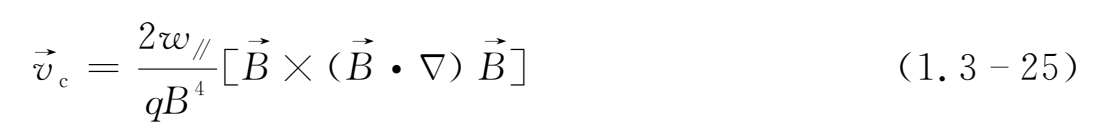
弯曲真空场:
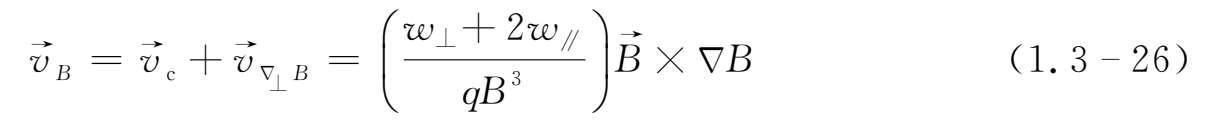
必须指出,由(1.3-13)和(1.3-28)式可知,由电场力或与电性有关的等效力引起的漂移速度大小和方向均与带电粒子的质量及所带电荷大小、符号以及速度无关。即正负带电粒子将以相同的速度向同一方向漂移,它们将不会产生电流和宏观的电荷分离。同样,由(1.3-22)、(1.3-23)、(1.3-25)、(1.3-26)式可知,在非电性力作用下,漂移速度的方向随粒子电荷符号而改变,此时离子和电子向相反方向漂移,因此会引起电荷分离。由上可知,漂移运动具有令人惊奇的特性:电性力只引起质量的运动,而非电性力反倒引起电流。