




磁流体力学一方面考虑洛伦兹力对导电流体的运动所产生的力学作用,另一方面,由于导电流体相对于磁场运动而感应电动势,从而改变磁场的初始位形。为了阐明导电流体中磁场变化的特殊规律,本节暂不考虑洛伦兹力对导电流体运动的影响,而仅仅研究运动的导电流体对磁场的作用。
利用麦克斯韦方程(2.3-2b)式和欧姆定律(2.3-5)式,即
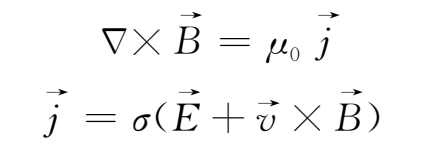
消去
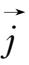 ,可得
,可得
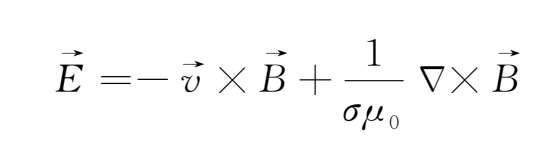
然后对上式取旋度,并考虑到
 ×
×
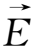 =-
=-
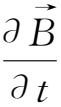 ,则有
,则有
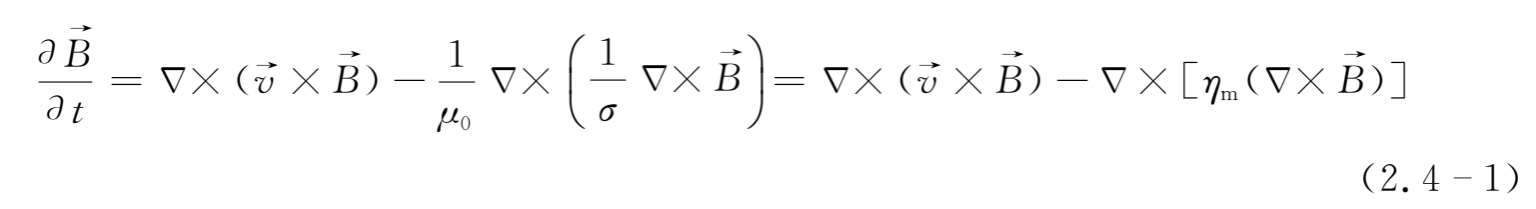
式中
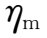 称为磁扩散系数,
称为磁扩散系数,
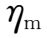 =
=
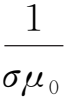 。上式就是导电流体中磁场变化所遵循的基本方程式,称作磁感应方程式。
。上式就是导电流体中磁场变化所遵循的基本方程式,称作磁感应方程式。
当电导率σ在空间上为均匀的常量时,利用矢量运算的恒等式
 ×
×
 ×
×
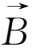 =
=
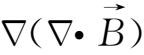 -
-
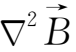 和磁场的无源性质,(2.4-1)式便化为
和磁场的无源性质,(2.4-1)式便化为
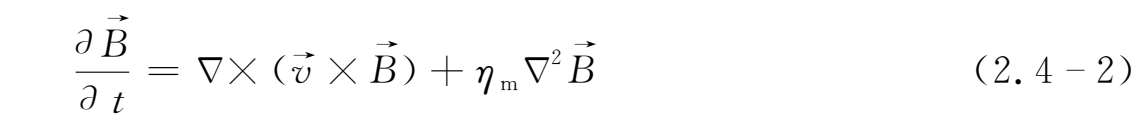
磁感应方程(2.4-1)式和(2.4-2)式表明,导电流体中磁场的变化由两个因素决定:①导电流体的运动情况;②磁场本身的分布位形。它们将给出导电流体和磁场相互作用的两个重要性质——磁场的扩散效应和冻结效应。
一般情况下,在估算导电流体中磁场的变化时,既不能忽略流体的运动,也不能把流体当作完全导电的理想流体来处理。这时在数学上必须求解磁感应方程(2.4-1)式或(2.4-2)式。求解磁感应方程式是十分困难的,为了能不解方程,而对所研究问题中有关物理量的大小有一个量级的概念,以建立粗略的物理图像并作出一些初步的判断,通常采用所谓量级分析法来处理微分方程式。尽管方法本身很粗糙,但却非常有用。应用量级分析法时,用有关物理量的特征数值代替微分方程式中相应的各项。例如用量级分析法来估算磁场方程(2.4-2)式中右端两项的大小时,可用所研究问题的特征长度L的倒数
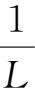 代替对空间的一阶导数,用
代替对空间的一阶导数,用
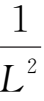 代替对空间的二阶导数,于是有
代替对空间的二阶导数,于是有
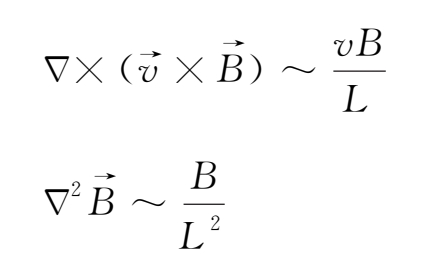
方程式(2.4-2)右端第一项与第二项的比值为
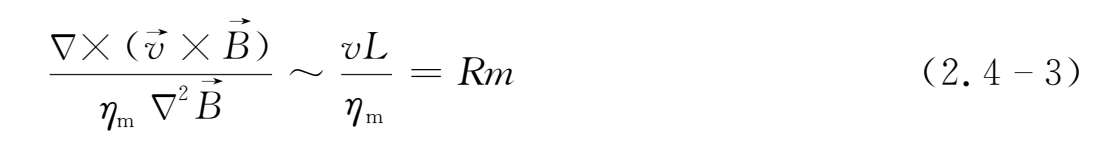
v、B分别为导电流体的运动速度和磁场强度的特征值,而Rm称作磁雷诺数。
显然,磁雷诺数Rm的大小直接表征了导电流体中磁场变化的主要决定因素。当Rm≫1时,磁感应方程式中右端第一项流动项起重要作用,磁场的变化主要由导电流体运动所决定;而当Rm≪1时,磁感应方程式中右端第二项即扩散项起主要作用,磁场的变化主要通过扩散而衰减和趋于均匀化。
通常宇宙等离子体都具有大的特征尺度,因此大磁雷诺数是磁流体力学问题的基本特征之一,宇宙等离子体的运动常常是天体磁场变化的主要原因。
当流体静止时,磁感应方程(2.4-2)式变为

上式是一个扩散方程,它表示在不运动的导电流体中,磁场随时间的变化是由磁场分布的不均匀所引起的。磁场将从强的区域向弱的区域扩散,扩散的结果使导电流体中的磁场分布趋向于均匀化,而总的磁场能量趋向于减小。由(2.4-4)式可知,磁场扩散的速率不但与磁场的不均匀性
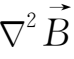 有关,还取决于导电流体本身的性质。磁扩散系数
有关,还取决于导电流体本身的性质。磁扩散系数
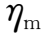 越大,磁场的扩散就越快。
越大,磁场的扩散就越快。
利用量级分析法可估算导电流体中磁场扩散的特征时间τ d ,对扩散方程(2.4-4)式应用量级分析法可得
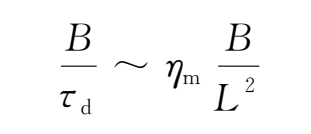
于是有
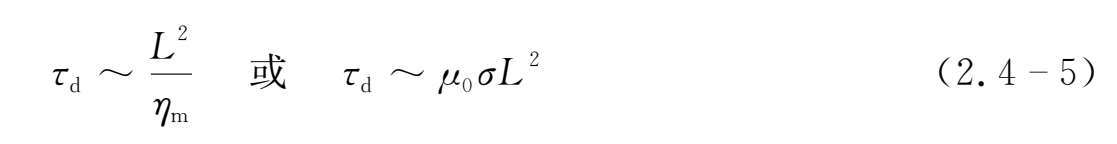
(2.4-5)式表明,导电流体的电导率越大,磁场衰减越慢。当σ→∞时,τ d →∞,磁场将不扩散,显然此时即为磁场冻结的情况。(2.4-5)式还表明,对于有限电导率的导电流体,其特征尺度越大,磁场的扩散速率便越小。所以,宇宙等离子体的巨大尺度使它们内部磁场的衰减具有很大的时标。
为了使读者对导电流体中磁场的扩散有较清晰的物理图像,下面以一维无限空间中磁场的扩散问题为例作说明。在一维情况下,扩散方程(2.4-4)式取如下形式

若导电流体的边界在很远或没有边界,这时只需考虑初始条件而不必考虑边界条件,这样的问题称作柯西问题。当满足初始条件
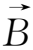 (x,0)=
(x,0)=
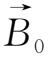 (x)时,扩散方程(2.4-6)式的柯西解为
(x)时,扩散方程(2.4-6)式的柯西解为
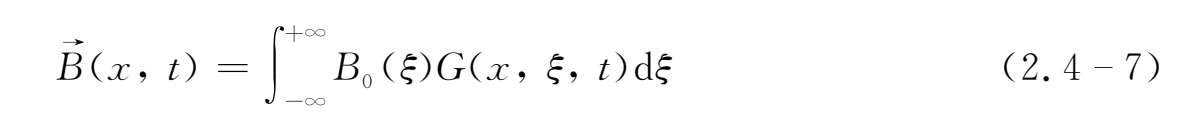
上式中格林函数G(x,ξ,t)为
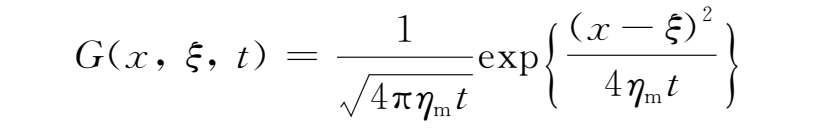
若磁场的初始条件为
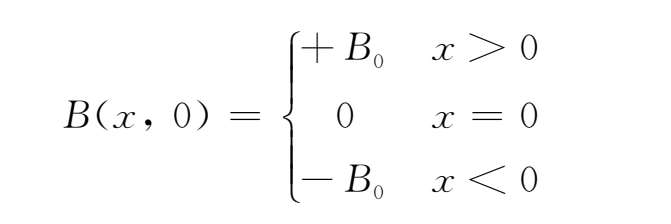
上式为电流片两侧磁场位形最简单的数学表示,B 0 为常数。代入(2.4-7)式,可得一维磁扩散方程的解为
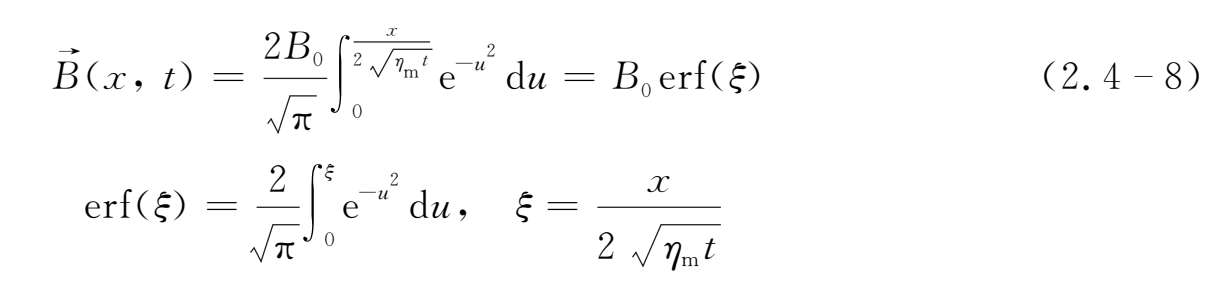
当ξ→∞时,erf(ξ)→±1,显然满足初始条件,当|x|≪
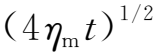 ,B(x,t)=
,B(x,t)=
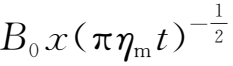 ,当t给定为某一时刻,则B(x,t)随x的变化为线性函数,而当|x|≫
,当t给定为某一时刻,则B(x,t)随x的变化为线性函数,而当|x|≫
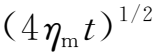 ,|B(x,t)|≈B
0
(详见图2.1)。
,|B(x,t)|≈B
0
(详见图2.1)。
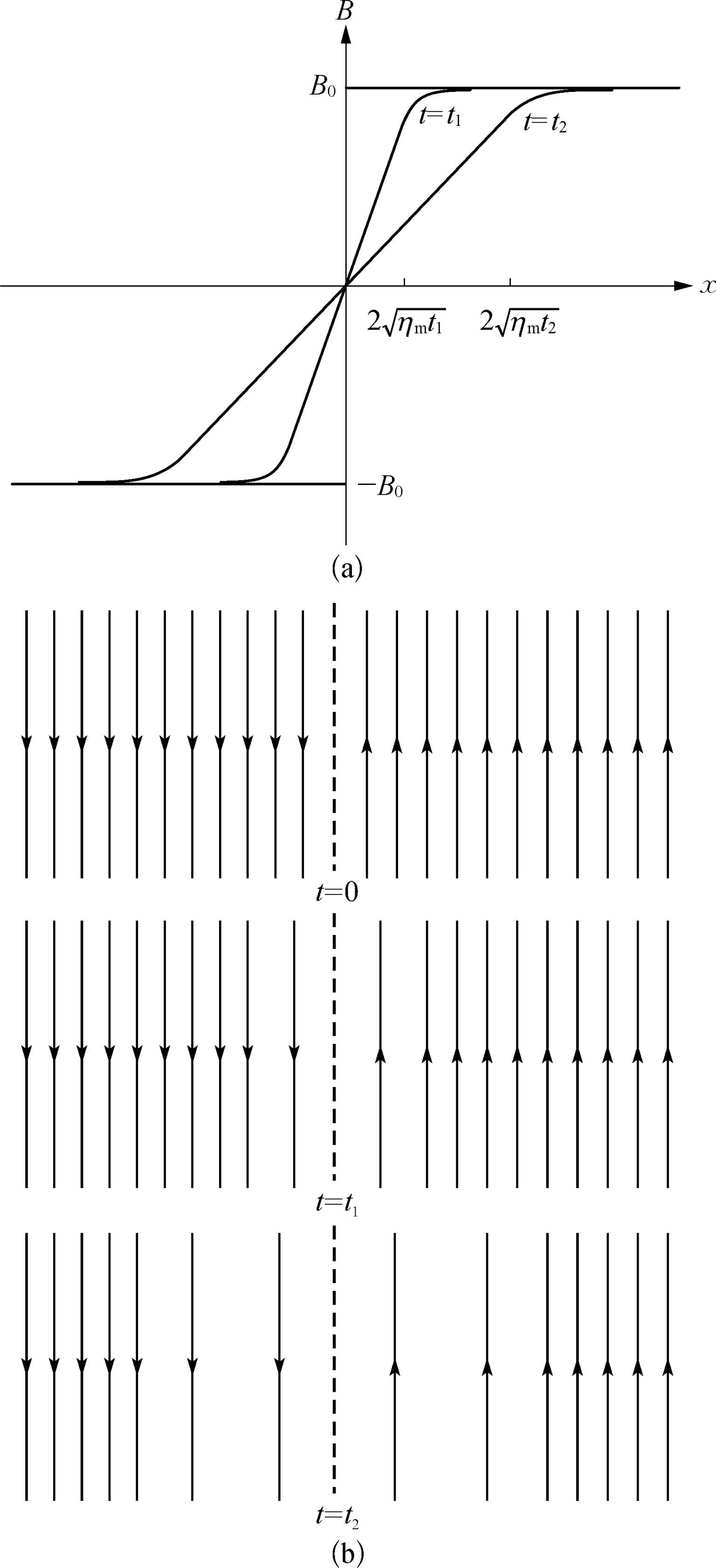
(a)磁场强度随时间的变化(b)磁力线随时间的扩散示意图
图2.1 电流片扩散示意图
图2.1(a)给出了不同时间t
1
和t
2
(t
2
>t
1
>0)的磁场强度的变化,图2.1(b)给出了不同时间相应磁力线扩散导致的磁力线疏密示意图。由图2.1可知,电流集中在宽度为l=4
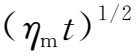 的区域,该区域称为电流片。由安培定律可知
的区域,该区域称为电流片。由安培定律可知
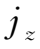 =
=
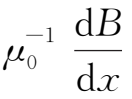 其宽度随时间t以
其宽度随时间t以
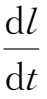 =2
=2
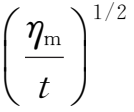 的速率增加。在电流片内,场强单调下降,当|x|≫
的速率增加。在电流片内,场强单调下降,当|x|≫
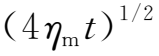 ,场强几乎是常数。电流片中的磁力线与其说是扩散出去了还不如说是被湮灭了,湮灭的本质是磁能通过欧姆耗散变为热能了。磁扩散近似时导电流体中的总磁能为
,场强几乎是常数。电流片中的磁力线与其说是扩散出去了还不如说是被湮灭了,湮灭的本质是磁能通过欧姆耗散变为热能了。磁扩散近似时导电流体中的总磁能为
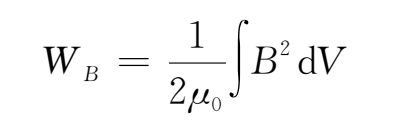
磁能的变化率为
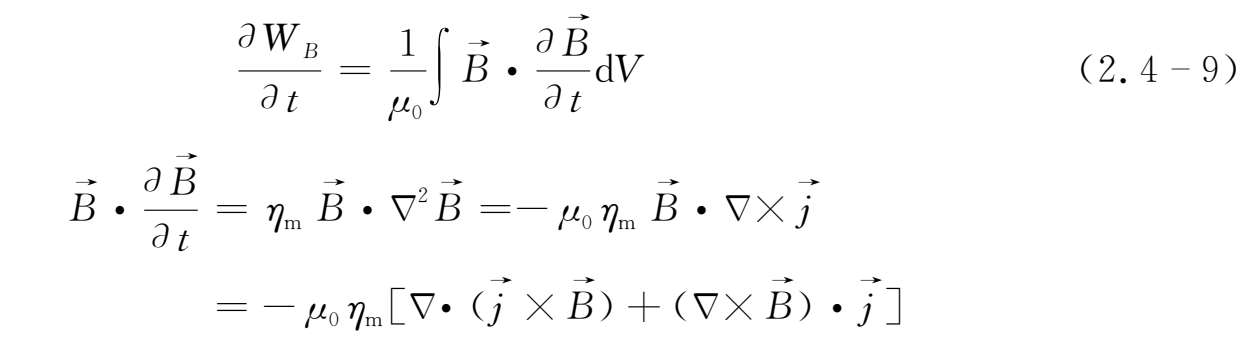
则
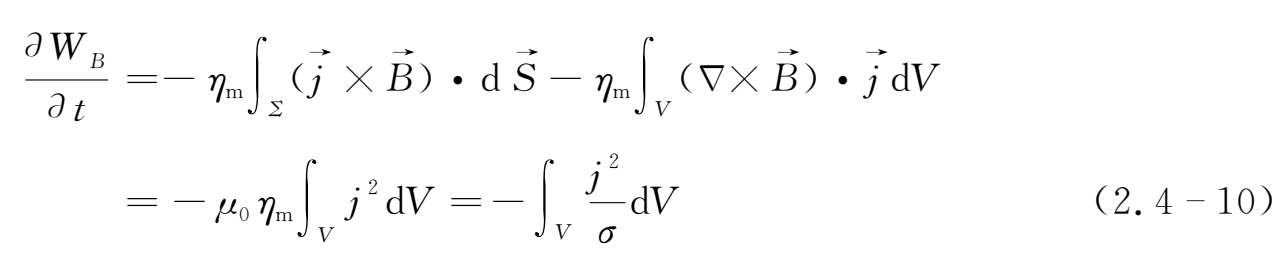
上式中由于边界面Σ上
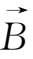 、
、
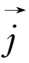 为零,所以面积分
为零,所以面积分
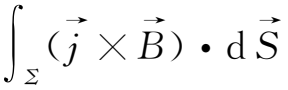 ≡0。(2.4-10)式表明,静止导电流体中磁场的扩散效应使总磁能减少,其本质是由电阻引起的焦耳耗散使磁能转变为导电流体的热能。因此可以认为导电流体中磁场的扩散与电磁能量的焦耳耗散是同一个物理过程,只是从不同的角度去描述它而已。由于在这个过程中,有序的磁能被转化为导电流体的无序热能,所以过程是不可逆的。
≡0。(2.4-10)式表明,静止导电流体中磁场的扩散效应使总磁能减少,其本质是由电阻引起的焦耳耗散使磁能转变为导电流体的热能。因此可以认为导电流体中磁场的扩散与电磁能量的焦耳耗散是同一个物理过程,只是从不同的角度去描述它而已。由于在这个过程中,有序的磁能被转化为导电流体的无序热能,所以过程是不可逆的。
当考虑Rm≫1时,方程(2.4-2)式将近似为

上式表明,这时磁场的变化将完全由流体的运动所决定,(2.4-11)式在形式上与无黏滞不可压流体中涡旋
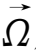 所满足的方程一样
所满足的方程一样

(2.4-12)式的物理图像是,涡旋黏附在流体质点上,随流体一起运动。由此可见,(2.4-11)式意味着在完全导电的理想流体中,磁场的变化就如同磁力线黏附于导电流体质点上,随它一起运动。因此可形象地用磁力线“冻结”在流体上这样的概念来描述流体运动对磁场的影响,这就是所谓的磁场冻结效应,而(2.4-11)式也被称为冻结方程。
利用冻结方程(2.4-11)可以证明如下三个定理。①磁通量守恒定理:在完全导电的理想流体中,通过和流体一起运动的任意曲面的磁通量守恒。②在完全导电的理想流体中,起初位于某根磁力线上的流体质点,以后将一直位于这根磁力线上。③在理想磁流体力学条件下,对有限维的磁场结构,当且仅当在封闭曲面上,磁场和流场满足
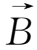 ·
·
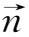 =
=
 =0,则磁螺度是一个守恒量。
=0,则磁螺度是一个守恒量。
考虑某一闭合回路l
1
所包围的面积S(t),随着等离子体一起运动,如图2.2所示,经过dt后,回路l
1
变成了回路l
2
,回路所包围的面积变成了S(t+dt)。运动过程中,回路所包围的面积在空间扫过的体积为δV,它的上底为S(t+dt),下底为S(t),侧面的面元为
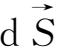 =
=
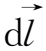 ×
×
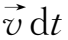 ,选择回路的方向,使得
,选择回路的方向,使得
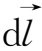 ×
×
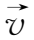 沿
沿
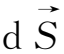 的外法线方向。这时,面元S(t+dt)的法线方向向外,而面元S(t)的法线方向向内。由于
的外法线方向。这时,面元S(t+dt)的法线方向向外,而面元S(t)的法线方向向内。由于
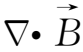 =0,则穿过包围小体积δV的封闭曲面的磁通量为零,即
=0,则穿过包围小体积δV的封闭曲面的磁通量为零,即
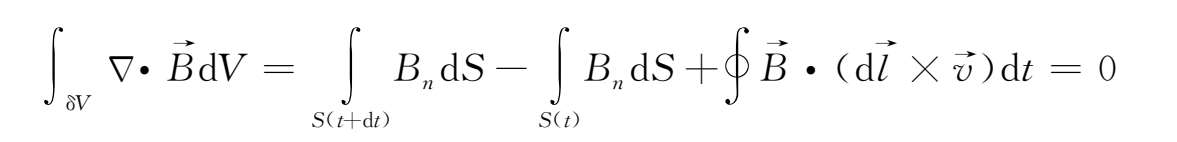
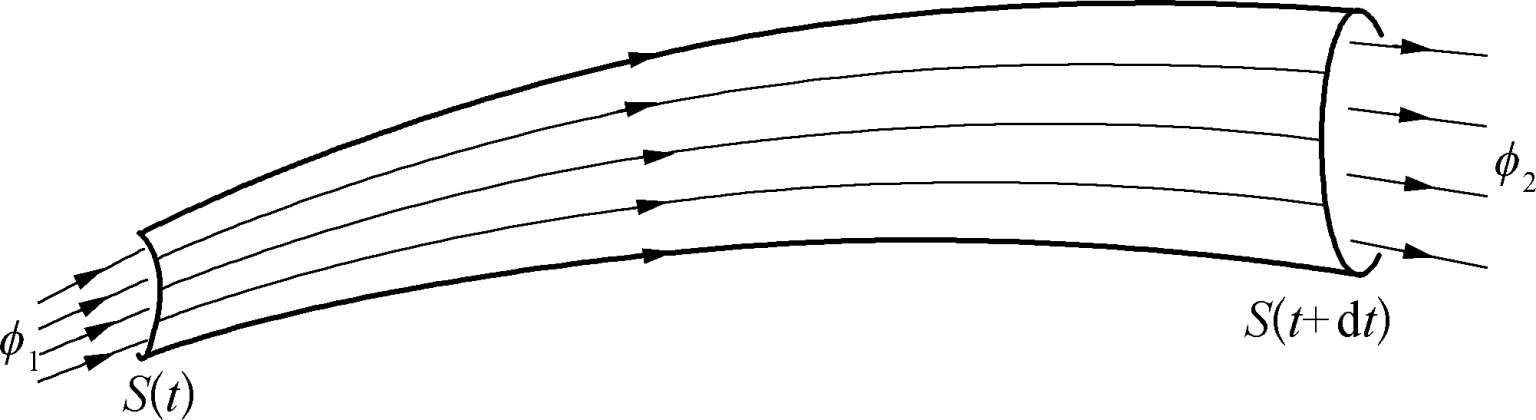
图2.2 闭合回路的运动
其中B
n
为磁场
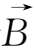 在面元S的法向分量,于是
在面元S的法向分量,于是
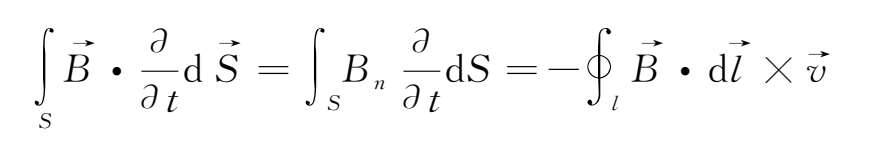
在上式中应用矢量公式
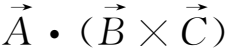 =
=
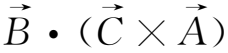 =
=
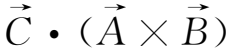 ,可得
,可得
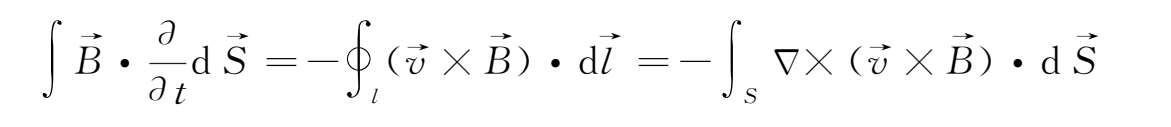
通过回路
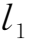 的磁通量为ϕ=
的磁通量为ϕ=
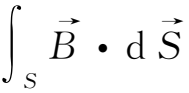 ,磁通量的变化率
,磁通量的变化率
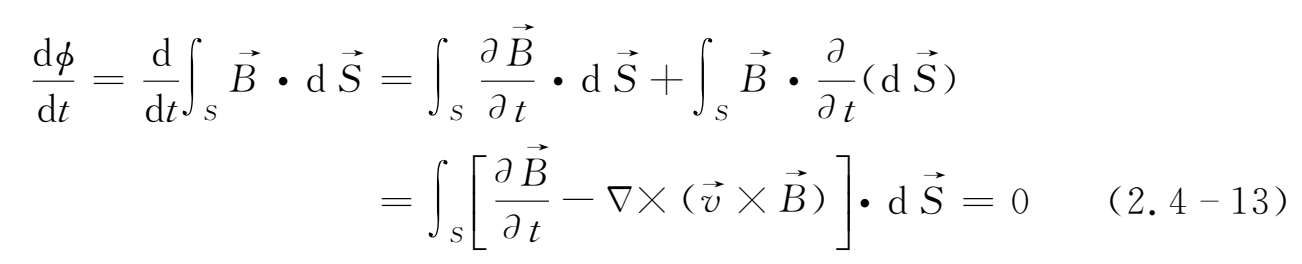
(2.4-13)式表明,在理想导电流体中,通过随流体运动的由固定的流体质点所组成的曲面时磁通量守恒。这一磁通量守恒定理是由柯林(Cowling)首先发现的,所以也叫作柯林定理。
下面证明第二个定理。考虑初始时刻t时,流体内任意两个位于一条磁力线上的相邻质点P 1 、P 2 如图2.3所示。在t+dt时刻,它们之间的距离将变为
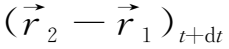 =
=
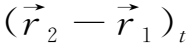 +
+
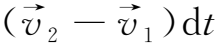
=
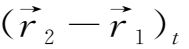 +
+
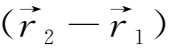 ·
·
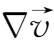 dt
dt
其中
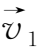 、
、
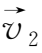 分别为质点P
1
、P
2
的速度。于是
分别为质点P
1
、P
2
的速度。于是
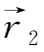 -
-
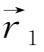 随时间的变化为
随时间的变化为
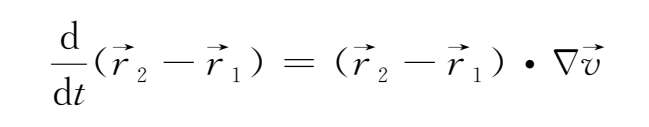
当两个质点无限接近时,则
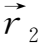 -
-
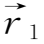 =
=
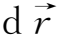 ,上述方程可写成
,上述方程可写成
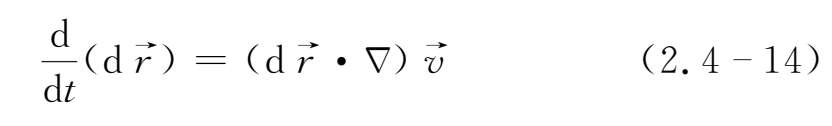
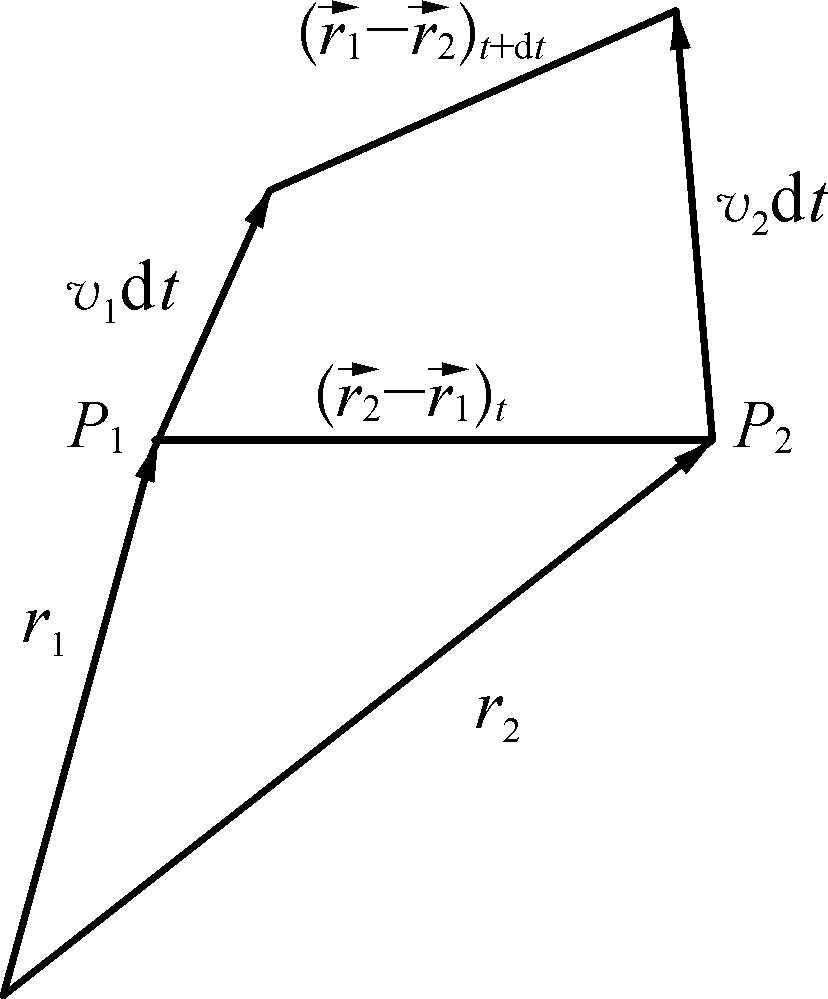
图2.3 流体质点的运动
另一方面,从冻结方程(2.4-11)式出发,利用矢量公式
 ×(
×(
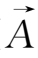 ×
×
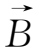 =
=
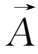
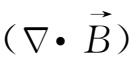 -
-
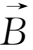 (
(
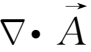 )+(
)+(
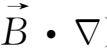 )
)
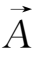 -(
-(
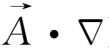 )
)
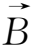 ,可得
,可得
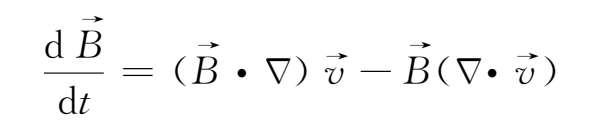
再代入连续性方程
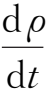 +
+
 =0 ,得
=0 ,得
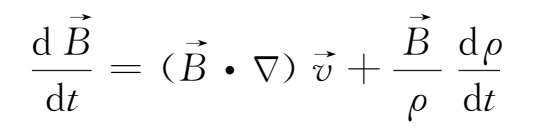
即

比较(2.4-14)和(2.4-15)式,可以看出矢量
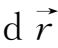 和
和
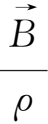 在完全导电流体中的演变满足同样形式的方程。这表明,若
在完全导电流体中的演变满足同样形式的方程。这表明,若
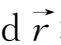 和
和
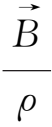 两矢量在初始时刻平行,则以后一直平行,而且它们的长度互成比例地改变。换言之,当t=0时流体元的
两矢量在初始时刻平行,则以后一直平行,而且它们的长度互成比例地改变。换言之,当t=0时流体元的
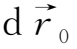 平行于
平行于
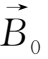 ,并正好位于这根磁力线上,即
,并正好位于这根磁力线上,即
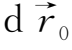 =
=
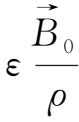 (ε为比例常数),则以后各时刻该流体元一直位于这根磁力线上,即一直有
(ε为比例常数),则以后各时刻该流体元一直位于这根磁力线上,即一直有

(2.4-16)式不仅说明磁力线仿佛“冻结”在和它一起移动的流体上,还表明在运动过程中流体元伸长或缩短时,磁场强度
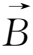 也随之成比例地增大或减小(当然前提是流体是不可压的)。(2.4-15)式首先由瓦伦(
也随之成比例地增大或减小(当然前提是流体是不可压的)。(2.4-15)式首先由瓦伦(
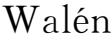 )在1946年得到的,所以该式也叫作瓦伦方程或瓦伦定理。
)在1946年得到的,所以该式也叫作瓦伦方程或瓦伦定理。
定义磁场结构的磁螺度为

式中
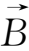 为磁场强度,
为磁场强度,
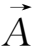 为磁场强度的矢势,标量
为磁场强度的矢势,标量
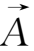 ·
·
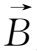 为磁螺度密度。
为磁螺度密度。
证明在理想磁流体力学条件下,对有限维的磁场结构,当且仅当在封闭曲面上,磁场和流场满足
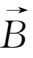 ·
·
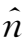 =
=
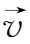 ·
·
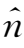 =0,则磁螺度是一个守恒量。
=0,则磁螺度是一个守恒量。
由磁螺度H的定义,又
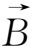 =
=
 ×
×
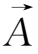 ,
,
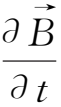 =
=
 ×(
×(
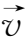 ×
×
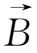 ),则
),则

可求磁螺度的变化率
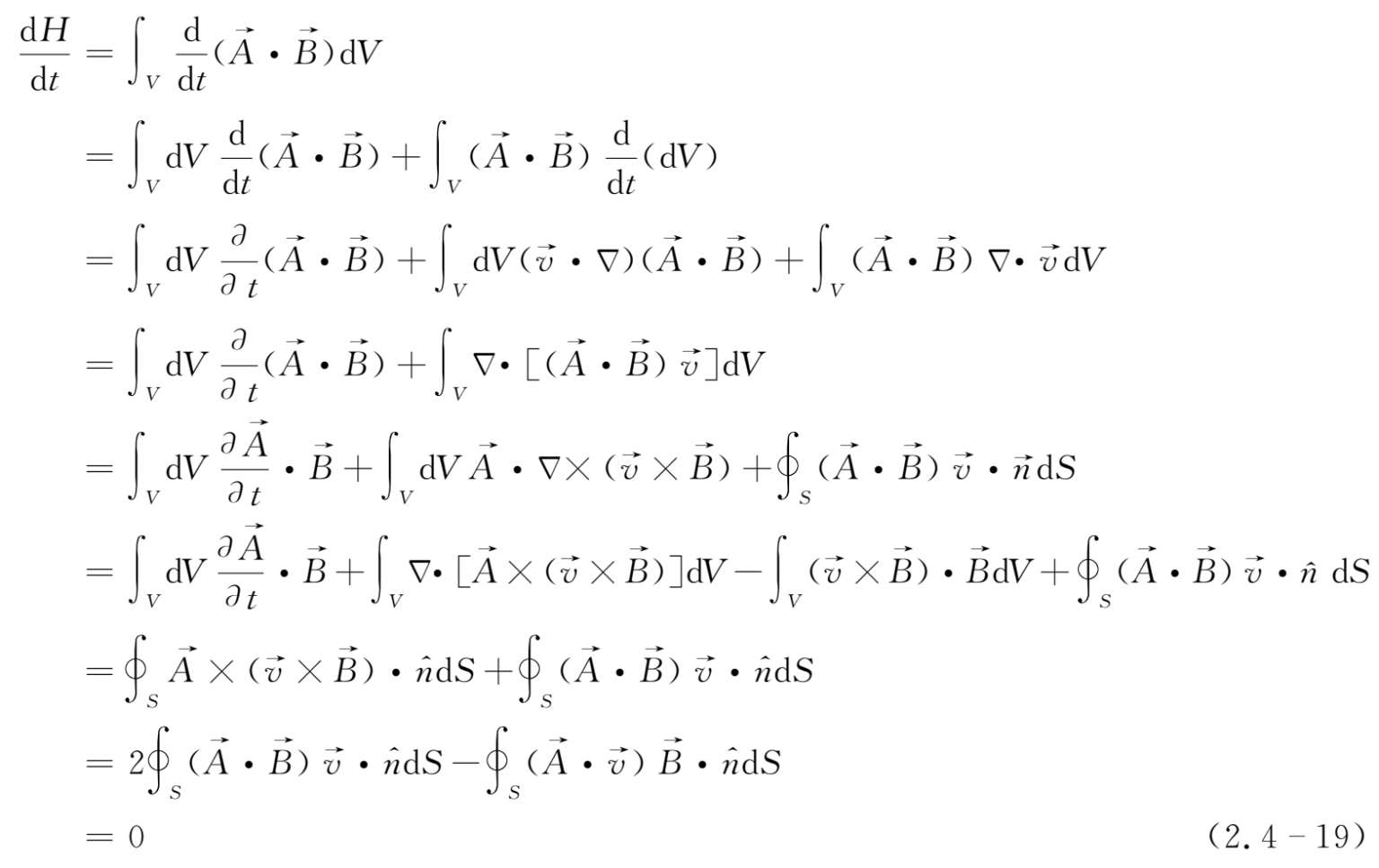
上式推导中应用了矢量公式
 ·(
·(
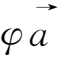 )=
)=
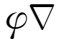 ·
·
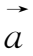 +
+
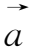 ·
·
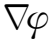 和
和
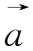 ×(
×(
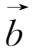 ×
×
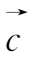 )=
)=
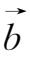 (
(
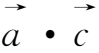 )-
)-
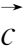 (
(
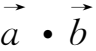 )。考虑到在封闭曲面上
)。考虑到在封闭曲面上
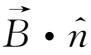 =
=
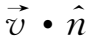 =0,故
=0,故
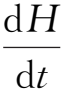 =0。所以磁螺度在理想磁流体中是一个守恒量。磁螺度是表征磁螺管内部的扭绕(twisting和kinking,叫作内螺度)和不同磁螺管之间耦合或交连(linkage)程度(叫作互螺度)的物理量。由于磁矢势在空间的变化
=0。所以磁螺度在理想磁流体中是一个守恒量。磁螺度是表征磁螺管内部的扭绕(twisting和kinking,叫作内螺度)和不同磁螺管之间耦合或交连(linkage)程度(叫作互螺度)的物理量。由于磁矢势在空间的变化
 ×
×
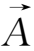 反映了矢量磁场,因此磁矢势
反映了矢量磁场,因此磁矢势
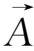 及由其计算的磁螺度H在一定程度上反映了磁场的拓扑结构,在理想导电磁流体中其拓扑磁结构是不变的。为使我们对磁螺度有更直观的理解,假设当磁螺管(N个)从初始势场状态经受了扭绕和交连之后,由于磁螺管内部的扭绕产生的内螺度为H
s
,磁螺管之间的交连产生的互螺度为H
m
,则整体的磁螺度可写为
及由其计算的磁螺度H在一定程度上反映了磁场的拓扑结构,在理想导电磁流体中其拓扑磁结构是不变的。为使我们对磁螺度有更直观的理解,假设当磁螺管(N个)从初始势场状态经受了扭绕和交连之后,由于磁螺管内部的扭绕产生的内螺度为H
s
,磁螺管之间的交连产生的互螺度为H
m
,则整体的磁螺度可写为
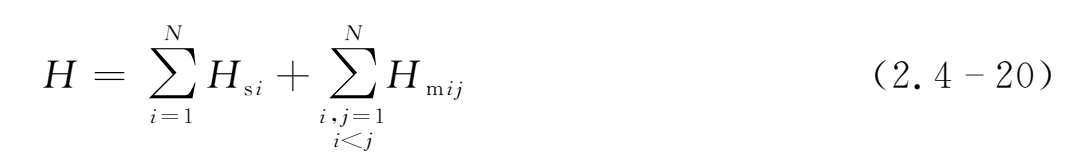
其中

Φ t 为回旋变换角〔详见3.4节(3.4-11)式〕,ϕ i 、ϕ j 为磁通量,L ij 为交连数,交连数L的正、负号如图2.4规定。即L的正、负遵循右手定则,即右手四指的方向沿曲线1的方向,大拇指的方向若与曲线2的方向一致,L取正号[图2.4(a)],反之取负号[图2.4(b)]。
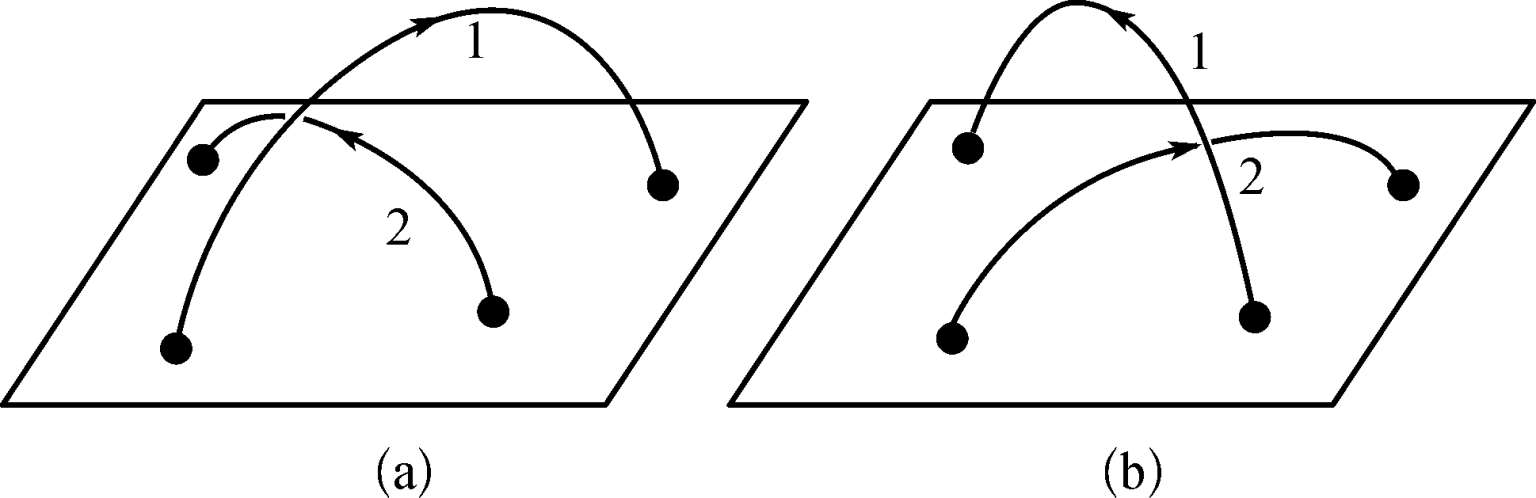
图2.4 两条磁力线正交连(a)和负交连(b)的规定
例如图2.5中的两个封闭而交连的磁力线管,其磁螺度值为
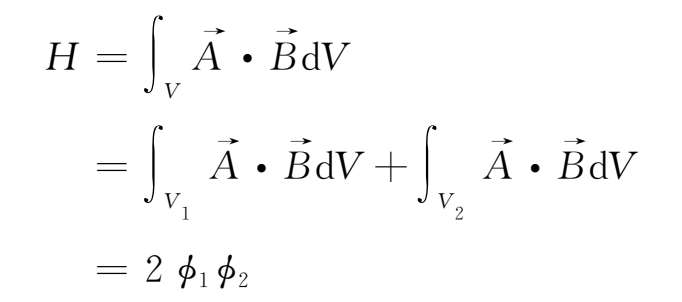
计算第一个积分
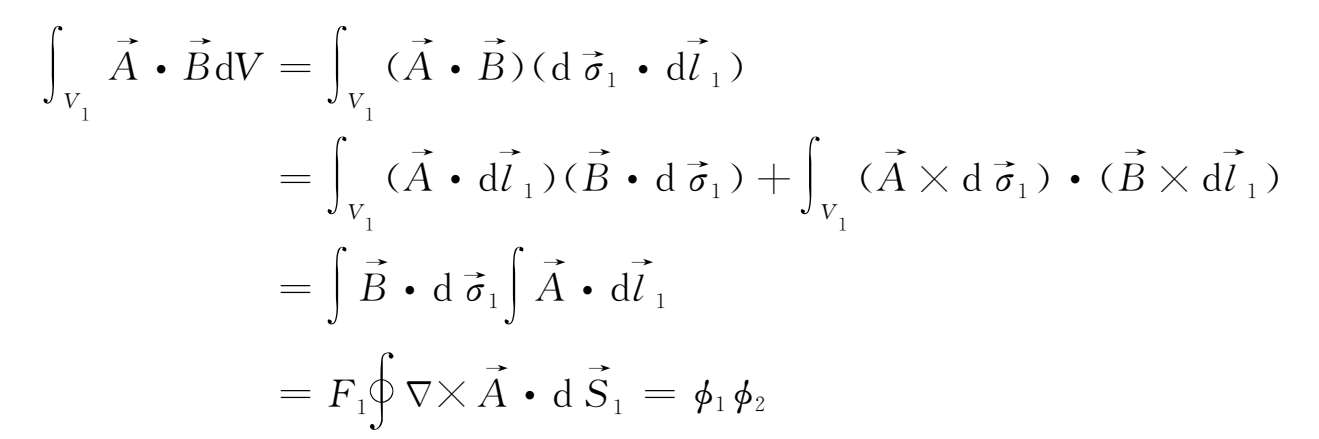
上式推导中应用了矢量公式(
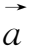 ×
×
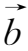 )·(
)·(
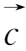 ×
×
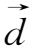 )=(
)=(
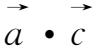 )(
)(
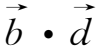 )-(
)-(
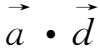 )(
)(
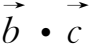 ),第二个积分的推导与它相同。而对于两根彼此不交连的磁通量管(如图2.6所示),因为通过S
1
面的磁通量为零,故此时磁螺度为零。因此磁螺度H的值和磁场的拓扑结构有关。又如图2.7所示的两类多次交连的磁通量管分别具有磁螺度为H=-3ϕ
2
和H=+3ϕ
2
。
),第二个积分的推导与它相同。而对于两根彼此不交连的磁通量管(如图2.6所示),因为通过S
1
面的磁通量为零,故此时磁螺度为零。因此磁螺度H的值和磁场的拓扑结构有关。又如图2.7所示的两类多次交连的磁通量管分别具有磁螺度为H=-3ϕ
2
和H=+3ϕ
2
。

图2.5 磁通交连示意图
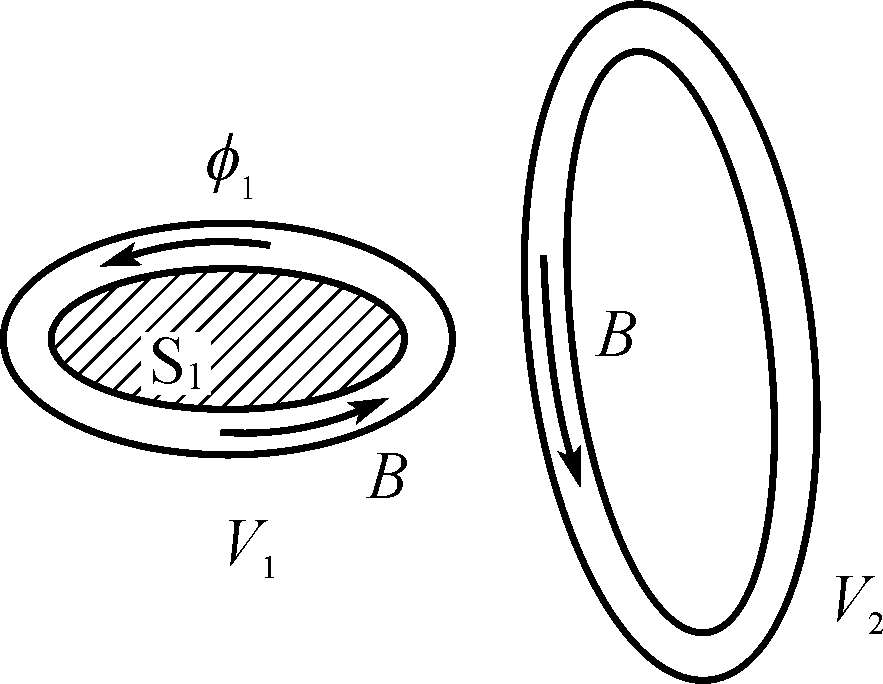
图2.6 磁通不交连示意图
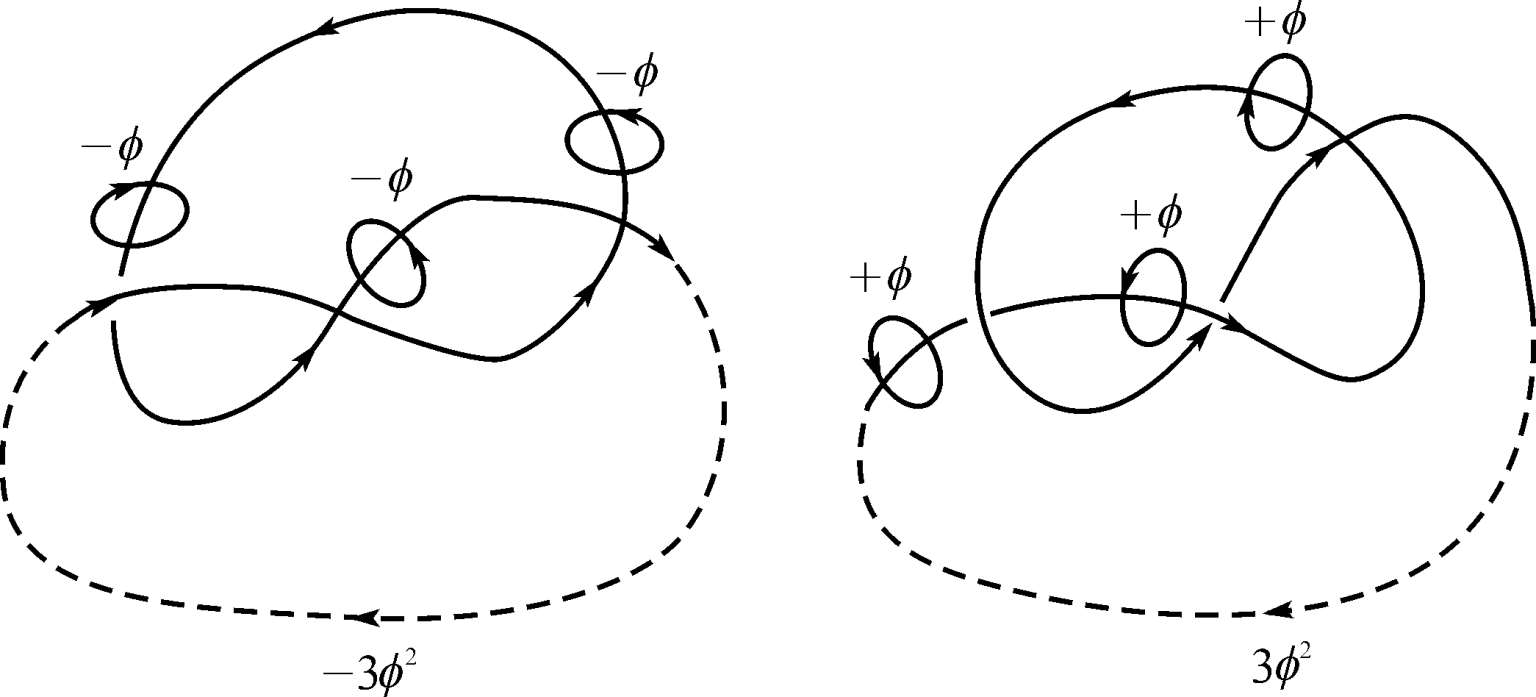
图2.7 两类磁通多次交连示意图
磁螺度H在理想磁流体中是不变量,其物理意义与磁力线冻结等价,即这时在某个磁面(在理想磁流体处于平衡位形时,由等压面上的磁力线组成的曲面叫磁面)内的磁力线在随时间变化时不会跑出磁面,也不会增加或减少其扭绕程度,因而磁场的拓扑结构不会因磁场随时间变化而改变。但当理想磁流体条件不满足时,对电阻磁流体,H会因欧姆耗散而随时间改变。
下面来计算磁场冻结情况下磁能随时间的变化。将冻结方程(2.4-11)代入(2.4-9)式中,得
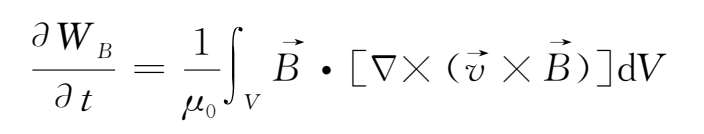
利用矢量公式
 ·(
·(
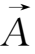 ×
×
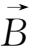 )=
)=
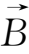 ·(
·(
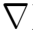 ×
×
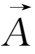 )-
)-
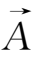 ·(
·(
 ×
×
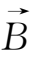 )和
)和
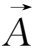 ·(
·(
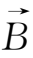 ×
×
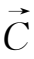 )=
)=
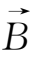 ·(
·(
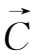 ×
×
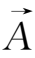 )=
)=
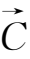 ·(
·(
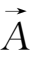 ×
×
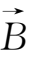 ),上式可化为
),上式可化为
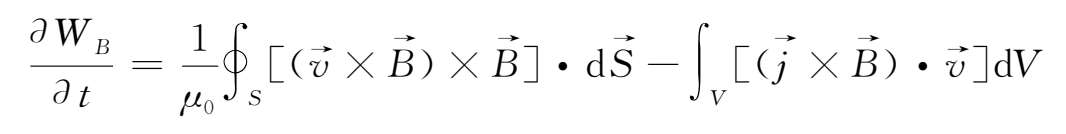
由于在边界面内
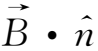 =
=
 =0故上式右端第一个面积分为零,于是得到
=0故上式右端第一个面积分为零,于是得到
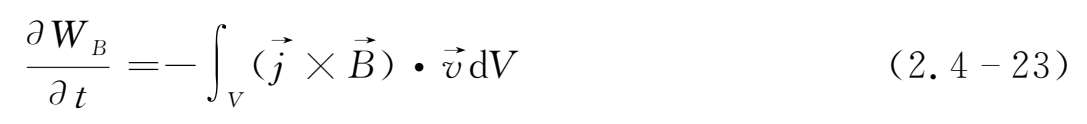
显然上式右端为单位时间内磁场对导电流体所做的功。它表明磁能的损失转化为导电流体的机械能。如果磁场做负功,则磁能将增加,磁能的增加将以导电流体机械能的减少为代价。与磁扩散情况下磁能的单向减少不同,在冻结情况下存在着磁能和导电流体机械能之间的相互转化。由于磁冻结情况下σ→∞,导电流体中焦耳耗散趋于零,磁能不可能转化为热能,此时磁能与机械能之间的转化是唯一形式。在这种磁场冻结的情况下,当垂直于局部磁场的方向中出现速度切变时,磁力线即将被流动所拉长,在垂直于原磁场的方向中便出现新的磁场,这样便得到流动速度切变对磁场的放大作用。
为方便起见,利用拉格朗日变数来计算切变流对磁场的放大作用。令
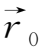 和
和
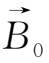 分别为t=0时流点的位置和磁场,则在t=t时该流点已运动到
分别为t=0时流点的位置和磁场,则在t=t时该流点已运动到
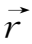 =
=
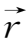 (
(
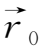 ,t),该处的磁场为
,t),该处的磁场为
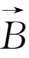 =
=
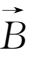 (
(
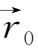 ,t)。在σ=∞时,瓦伦方程(2.4-15)即
,t)。在σ=∞时,瓦伦方程(2.4-15)即
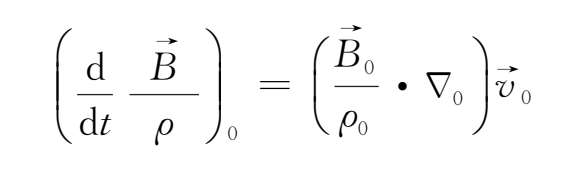
其中
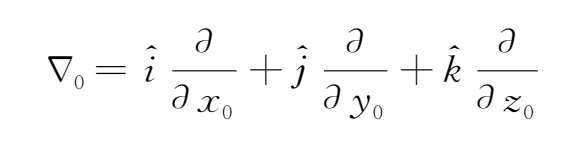
故
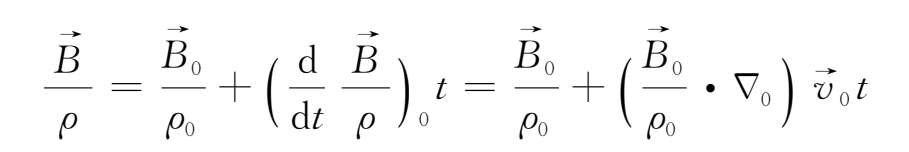
因
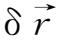 =
=
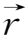 -
-
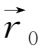 =
=
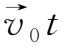 ,且
,且
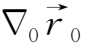 =
=
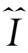 ,故上式为
,故上式为

应用此式可计算磁场强度与密度的比值随流动位置
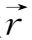 的演变。
的演变。
下面以不可压缩流体(ρ=ρ
0
)的二维流动为例,设流动限于x-y 平面上,则由(2.4-24)式,
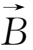 =(
=(
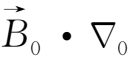 )
)
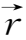 ,即
,即
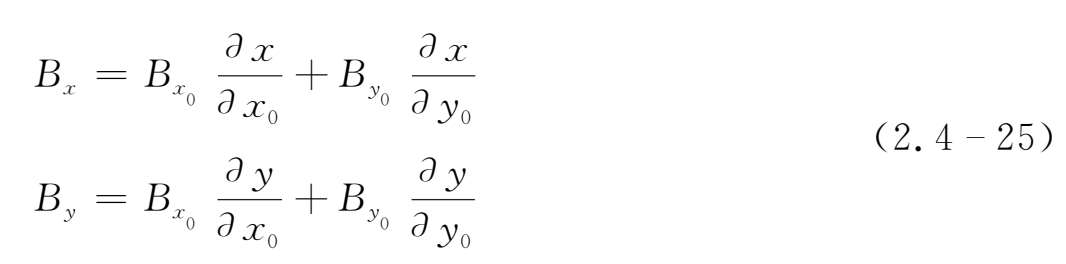
假定
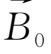 是均匀的,如图2.8(a)所示,
是均匀的,如图2.8(a)所示,
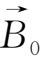 =
=
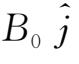 ,则沿y轴的流动并不影响磁场
,则沿y轴的流动并不影响磁场
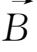 。故设流动为沿x轴的切变流动,即
。故设流动为沿x轴的切变流动,即

则
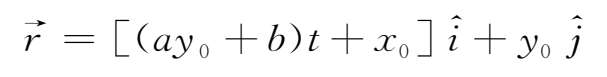
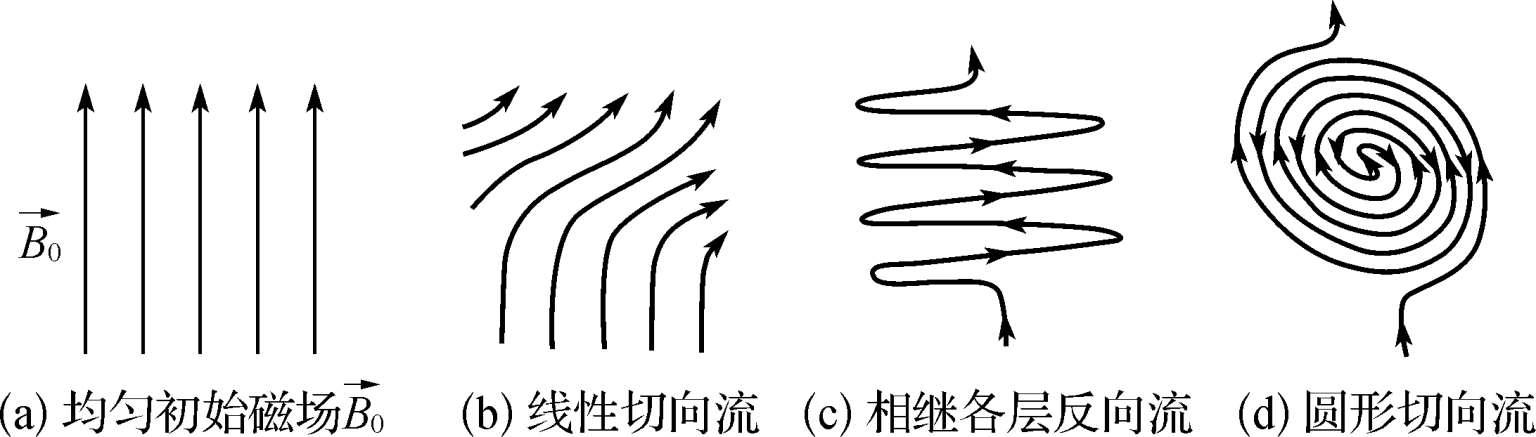
图2.8 切向流对磁力线作用的平面示意图
此式代入(2.4-25)式,得

如所预期,磁力线被切向流拉出了B x 分量,磁场强度增强了。若此流动局限在有限的区域中,则如图2.8(b)所示。在此区域中磁能密度亦增到

显然磁能的增加来自流体对磁场所做的功,它以消耗掉相同数量的流体动能为代价。
一般而言,磁力线被扭曲拉长时,磁场能量便增强。图2.8(c)及(d)表示在有限区域中两种这样的放大作用,(c)为相继各层有方向相反的流动所引起,(d)为转动切变所引起。这两种变化均由于切变流动引起了相继各层都有相反方向的磁场,都产生很大的磁场梯度。此时冻结效应不再成立,故磁感应方程(2.4-2)中必须考虑磁扩散项,虽扩散项的数值
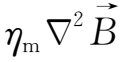 很小,但足以减小该磁场的放大效应。
很小,但足以减小该磁场的放大效应。
综上所述,理想磁流体中的冻结效应绝不是意味着磁力线僵化不动,它仅仅是给出了在完全导电的理想流体中,磁场的变化和流体运动或磁场的拓扑结构之间满足的一种关系。或者说,它规定了理想磁流体中磁场变化所必须遵循的一个特殊规律。它是磁流体力学中的基本规律之一,且有多方面的应用。例如冻结效应给予我们这样一种可能性,如果已知理想磁流体的运动情况,可估算磁场位形的变化,反之亦然。如果在某些天体物理问题中,已知等离子体的动能密度远小于磁能密度(即β=
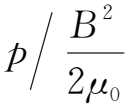 ,所谓小β问题),这时磁场对等离子体的运动起着控制作用,在冻结效应成立的前提下,可以肯定等离子体将沿磁力线运动。太阳大气中爆发日珥、日浪和喷流等均属此情况。反之如果β≫1,等离子体的动能密度远大于磁能密度,这时等离子体的运动将对磁场的变化起主导作用。冻结效应表明磁场的位形完全由等离子体的运动情况所决定。太阳风从太阳大气中带出磁场,形成行星空间中磁场的特殊分布就属于这类情况。在太阳物理中,光球磁场的观测表明,光球中磁螺度可以源源不断地输入到日冕之中,并且,在太阳的南半球输入的螺度为正号,在北半球则为负号。由于磁螺度在理想磁流体中为守恒量,日冕中的磁螺度难以消失和被耗散,所以磁螺度会在太阳南、北半球积聚起来。磁螺度的积聚可以存储磁自由能,它是否能解决日冕物质抛射的起源问题?或者说是否日冕物质抛射是日冕磁螺度积累的必然结果?至少磁螺度的研究为解决“日冕物质抛射起源”的科学问题提供了一个可能的途径。
,所谓小β问题),这时磁场对等离子体的运动起着控制作用,在冻结效应成立的前提下,可以肯定等离子体将沿磁力线运动。太阳大气中爆发日珥、日浪和喷流等均属此情况。反之如果β≫1,等离子体的动能密度远大于磁能密度,这时等离子体的运动将对磁场的变化起主导作用。冻结效应表明磁场的位形完全由等离子体的运动情况所决定。太阳风从太阳大气中带出磁场,形成行星空间中磁场的特殊分布就属于这类情况。在太阳物理中,光球磁场的观测表明,光球中磁螺度可以源源不断地输入到日冕之中,并且,在太阳的南半球输入的螺度为正号,在北半球则为负号。由于磁螺度在理想磁流体中为守恒量,日冕中的磁螺度难以消失和被耗散,所以磁螺度会在太阳南、北半球积聚起来。磁螺度的积聚可以存储磁自由能,它是否能解决日冕物质抛射的起源问题?或者说是否日冕物质抛射是日冕磁螺度积累的必然结果?至少磁螺度的研究为解决“日冕物质抛射起源”的科学问题提供了一个可能的途径。
此外,由定常的磁冻结方程,可直接推导出等旋转定律(或称为费拉罗等旋定律)。定常条件下的冻结方程为

选取柱坐标(r,
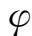 ,z),单位矢量为(
,z),单位矢量为(
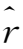 ,
,
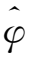 ,
,
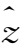 ),z轴与流团的旋转轴重合。假定转动是纯转动(不一定为刚性转动),即
),z轴与流团的旋转轴重合。假定转动是纯转动(不一定为刚性转动),即
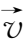 =ωr
=ωr
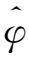 ,式中ω仅为r和z的函数。由于旋转的对称性,则
,式中ω仅为r和z的函数。由于旋转的对称性,则
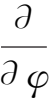 =0,所以
=0,所以
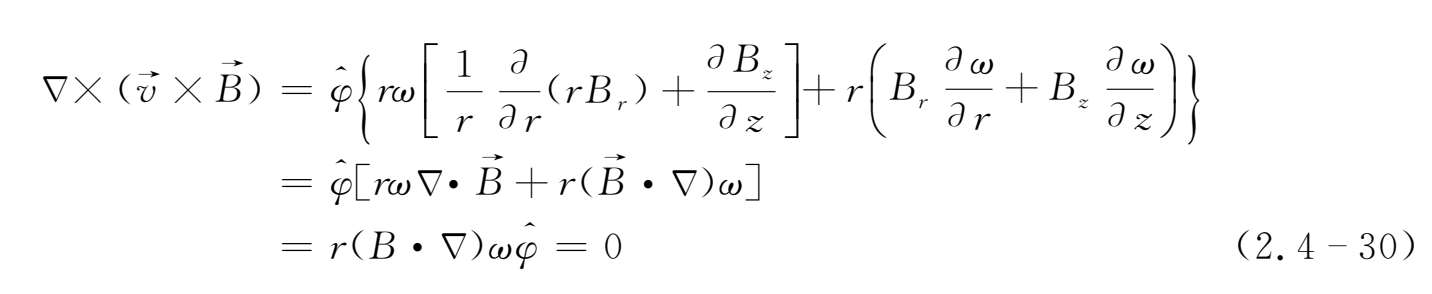
即

由(2.4-31)式可知在定常状态下角速度沿磁力线不变。(2.4-31)式即为费拉罗等旋定理。磁化恒星附近有一个密度较高的等离子体(σ→∞),考虑到星体与等离子体之间有角动量传递,这一等离子体绕轴旋转的角速度大致等于星体自转的角速度。所以,可以说冻结效应是用来分析研究等离子体问题的一个有力工具。
上面讨论了导电流体和磁场相互作用的两种极端情况。一般情况下,不能把导电流体看成是理想导电的,也不能忽略流体运动的影响,因此磁场的扩散和冻结将同时存在。