




当微波频段的电磁波照射到海面上时,由于海水的导电性较强,使得电磁波的趋肤深度很小,所以通常将海面的电磁散射问题看成是粗糙面上半空间的面散射问题。传统海面电磁散射的计算模型主要包括:基尔霍夫近似法(Kirchhoff Approximation Method,KAM)、微扰法(Small Perturbation Method,SPM)以及基于以上两者发展起来的复合表面模型(Composite Surface Model,CSM),亦称为双尺度模型(Two Scale Model,TSM)等解析近似方法和精确数值模拟方法。但随着研究的深入,以上传统方法逐渐显现出各自的不足,主要表现在针对大场景(包含尾迹)海面散射场空间分布计算和相位准确描述方面。为此,本节从这些复合表面模型中甄选出海面的Bragg散射理论和考虑角度截断的半确定面元散射模型(Semi-deterministic Facet Scattering Model,SDFSM)加以介绍,并在此基础上,开展海面的电磁散射场分析。
实验观测表明,当电磁波入射到海面时,入射波与海浪中特定频率分量作用形成的散射波会存在相干叠加效应——Bragg谐振效应,Bragg谐振效应造成的散射贡献称作Bragg散射。
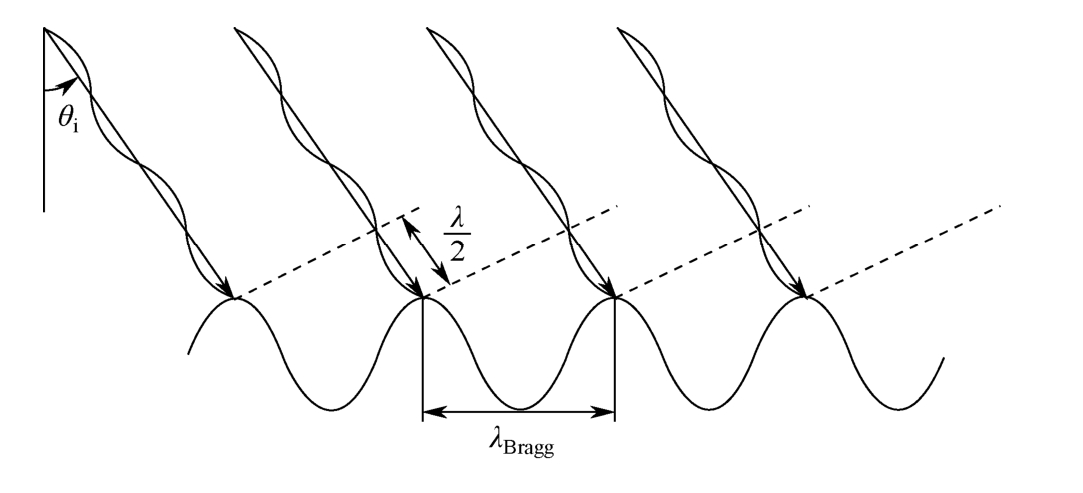
图1-13 一维海面Bragg散射示意图
图1-13给出了一维海面Bragg散射示意图,与入射电磁波发生谐振的海浪分量称作Bragg波,发生谐振的Bragg波矢量等于两倍入射波矢量的水平投影,则Bragg波波长 λ Bragg 、雷达波长 λ 以及本地入射角 θ i 可表示如下:

考虑到二维海面情况下,海浪波脊与雷达入射平面夹角为 φ 时,式(1-20)可转化为
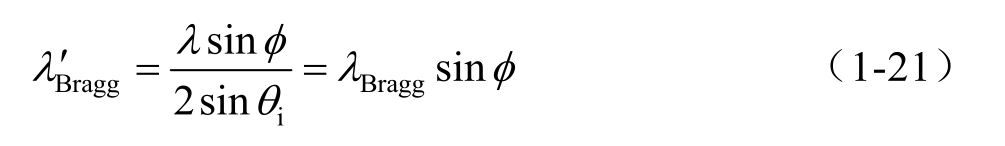
对多数单站雷达而言,当电磁波以中等入射角照射到海表面时,除去特别高的海况条件下,雷达接收到的后向回波中直接的镜向反射成分微乎其微。此时,Bragg散射是雷达散射的主要机制。此外,通过倾斜调制、流体动力调制和速度聚束效应,更长的重力波可以通过影响Bragg散射来影响散射空间分布。时空变化的海面风速、大气边界层的分层变化和海洋上层运动(如海洋锋、涡流、海底内波和舰船尾迹等)引起的流场变化均会影响海面的 Bragg散射分布。对于实际的二维海浪而言,Bragg波的尺度往往处在重力——毛细波或者毛细波之间,直接对海面上随机变化的小尺度毛细波特征进行离散采样或电磁计算往往困难且不现实,通常使用统计特性对海面 Bragg散射进行描述。统计特性包括其高度密度分布函数、自相关函数和方差谱等,本章使用基于海浪谱模型的SPM对海面 Bragg散射进行计算。在中等入射角条件下,SPM适用于以下海面条件:

式中, s s 表示海面的均方根斜率, σ s 表示小尺度粗糙面的均方根高度。
如图1-14所示,假设海面总体处于水平面 x o y 上,雷达入射平面为 x o z ,入射波和散射波分别为 k i 和 k s ,其对应 x o y 平面上的投影为 k 0 和 k 1 ,电磁波的散射角和散射方位角分别为 θ s 和 φ s 。Fuks [37,38] 给出了SPM的一阶散射幅度:
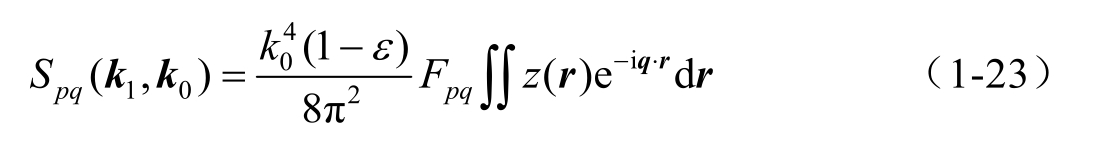
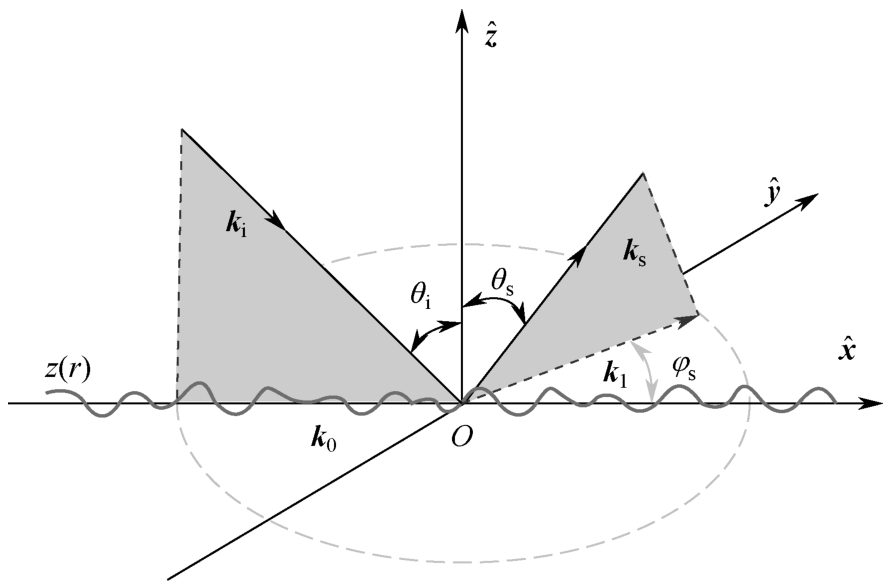
图1-14 SPM海平面散射示意图
式中, ε 表示海水的相对介电常数, F pq 表示SPM的极化核函数,下标 pq 分别表示散射波和入射波的极化特性,例如, F HV 表示散射波水平极化入射波垂直极化的核函数, q = k s -k i ,各极化条件下的SPM核函数定义如下:
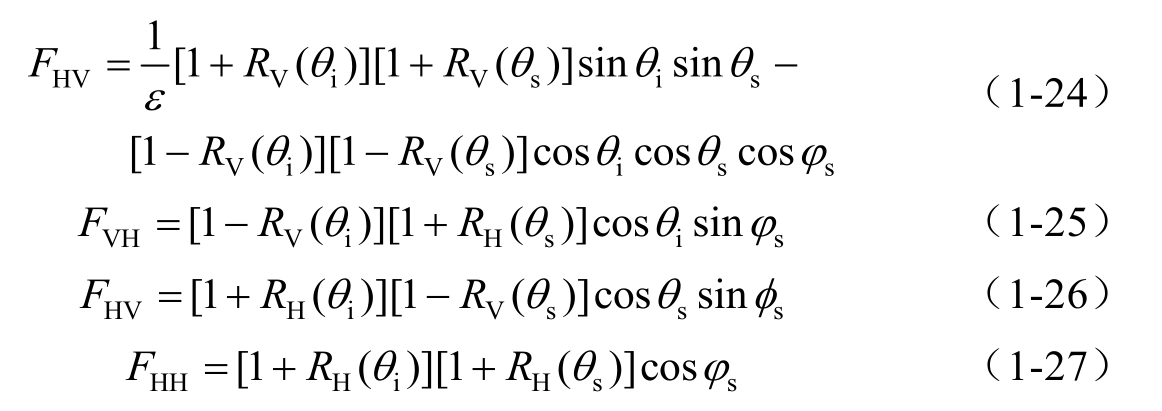
R H 和 R V 表示对应入射极化电磁波条件下的Fresnel反射系数:
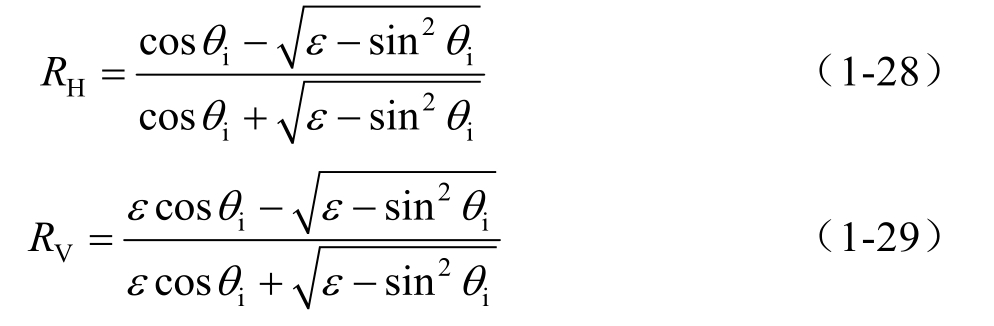
设海面散射源与接收雷达距离为 R ,则海面的远区散射场 E s 可表示为
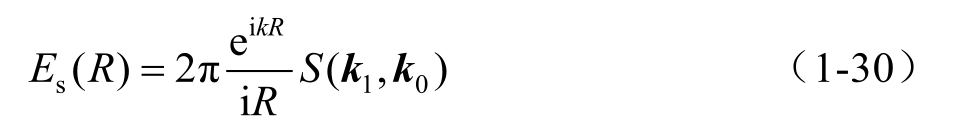
根据雷达散射截面定义,可以通过其统计平均值解析计算出一阶SPM下的归一化雷达散射截面(Normalized Radar Cross-Section,NRCS):
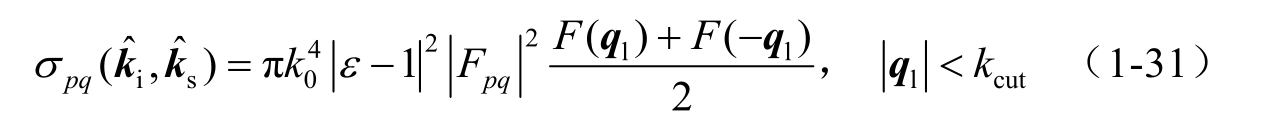
式中, F ( q l )即为对应 Bragg波矢量 q l 的海浪功率谱, q l 表示 q 在水平面上的投影矢量。 k cut 为截断波数,用于区分海面的大小尺度特征。
半确定面元散射模型属于复合表面散射理论中一种快速精确的海面散射建模方法。该模型按照海浪粗糙面的水平面投影对海面场景进行面元化离散,面元尺寸应大于10个入射波波长,使得面元内Bragg波分布情况更接近海浪谱的统计值,同时各个面元的散射贡献满足非相干性。对于实际的海浪模型,离散面元通常是倾斜的,面元散射模型主要通过局部坐标转换和KAM来对面元倾斜产生的调制效应和镜向反射贡献进行修正。半确定面元散射模型通过统计方式对每个倾斜离散面元求散射场,公式各项有着明确的物理意义,可以有效计算大场景随机风浪的面元散射分布与总散射场。
图1-15给出了海场景的全局坐标系与面元局部坐标系示意图,对于任一离散单元,设其均值面中点为局部坐标系的原点
O
l
,面元法向量
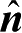 方向为
z
轴,
y
轴方向由入射波与法向量确定,建立一个局部坐标
方向为
z
轴,
y
轴方向由入射波与法向量确定,建立一个局部坐标
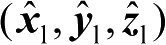 :
:
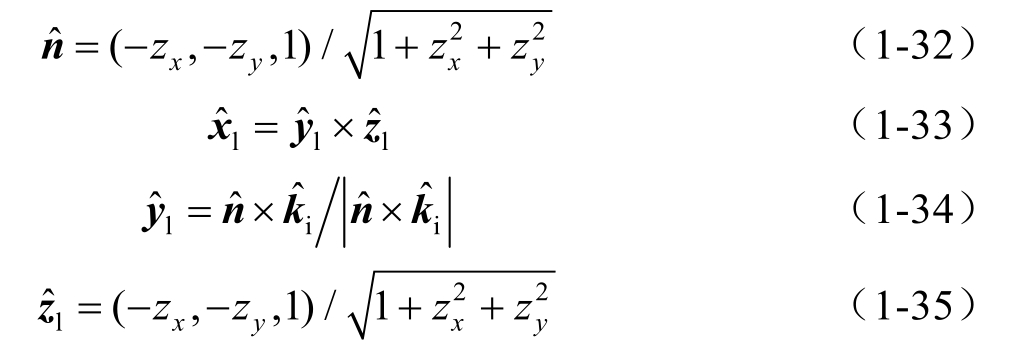
其中,
z
x
和
z
y
分别表示全局坐标系下离散面元
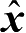 方向和
方向和
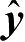 方向的斜率。
方向的斜率。
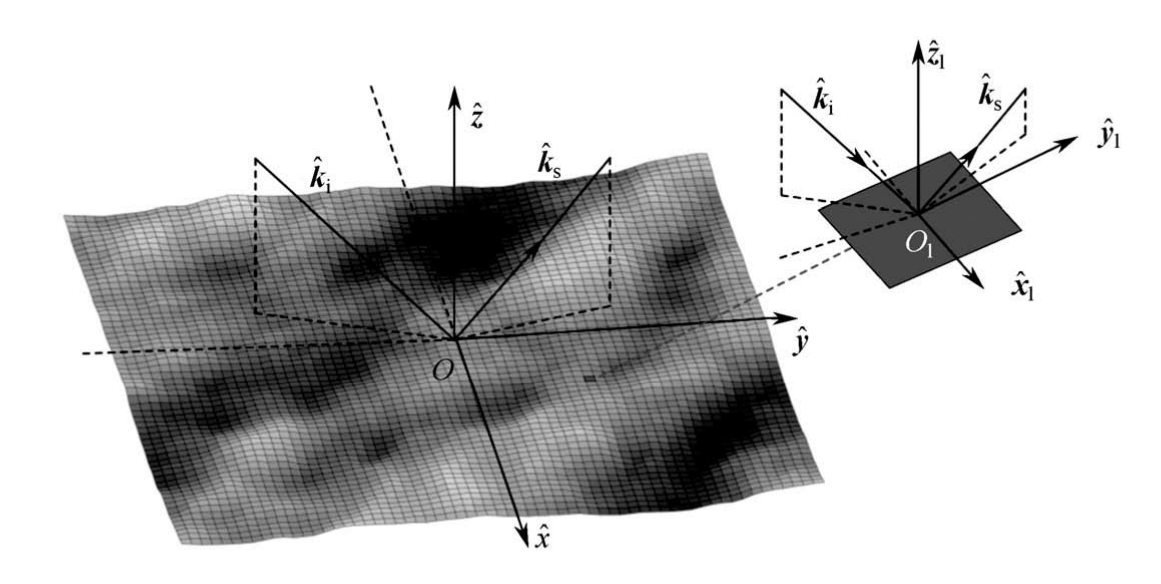
图1-15 海场景的全局坐标系与面元局部坐标系示意图
由全局与局部坐标系之间的转换关系,可以得到各电磁矢量在两种坐标系下的转换关系:
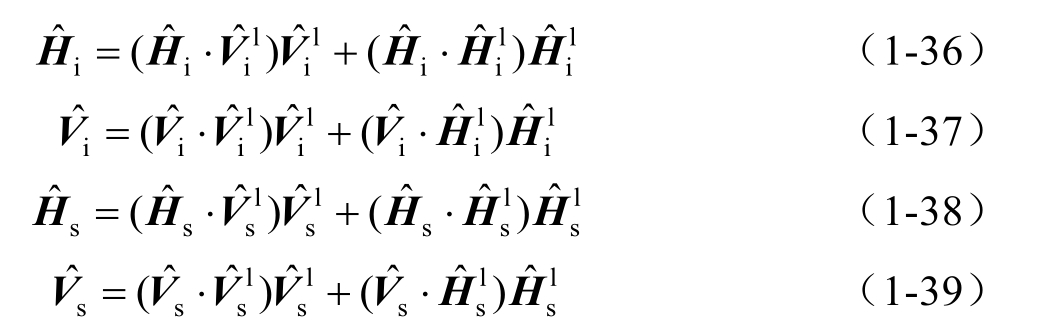
结合1.2.1节中的 SPM核函数,则对应全局坐标系中的 SPM核函数可以表示为以下矩阵形式:
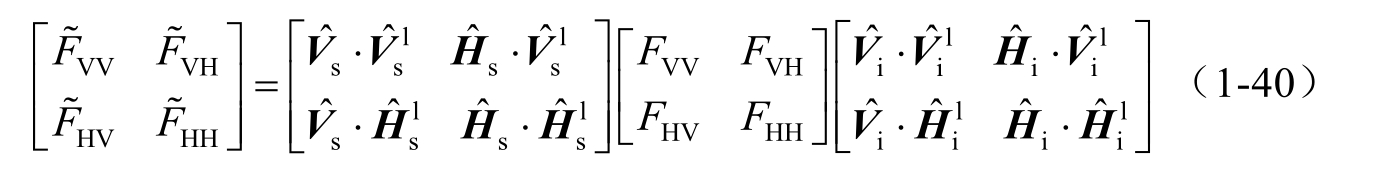
则在中等入射角范围内,可得倾斜面元散射模型的散射系数表示如下:
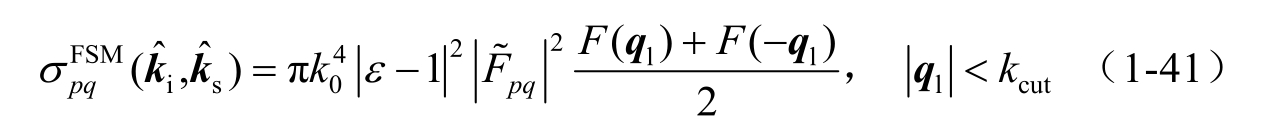
若面元对应的本地入射角较小,海面大尺度长波引起的镜向反射贡献急剧增加,面元散射模型使用KAM来对这部分电磁散射贡献进行修正。KAM基于切平面假设,即假定随机粗糙表面在每个表面点处都可以视为局部平坦的平面,散射贡献仅由其镜像方向产生。该假设适用条件如下:
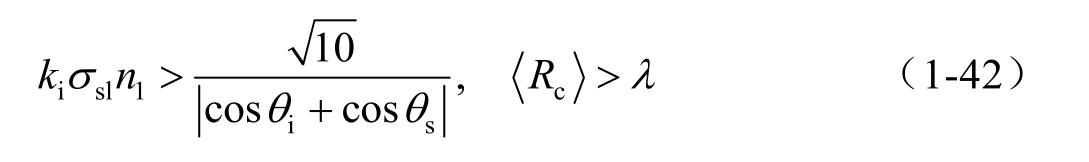
式中, σ sl 表示大尺度粗糙面的均方根高度。 n 1 表示入射介质的相对折射率,对于空气可近似地取 n 1 =1。KAM散射系数可使用统计方法表示为
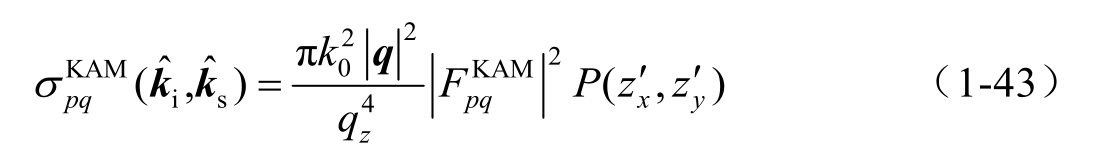
式中,
q
z
表示
q
在面元垂直方向上的分量,
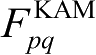 表示其下标对应极化条件下的镜向反射核函数:
表示其下标对应极化条件下的镜向反射核函数:
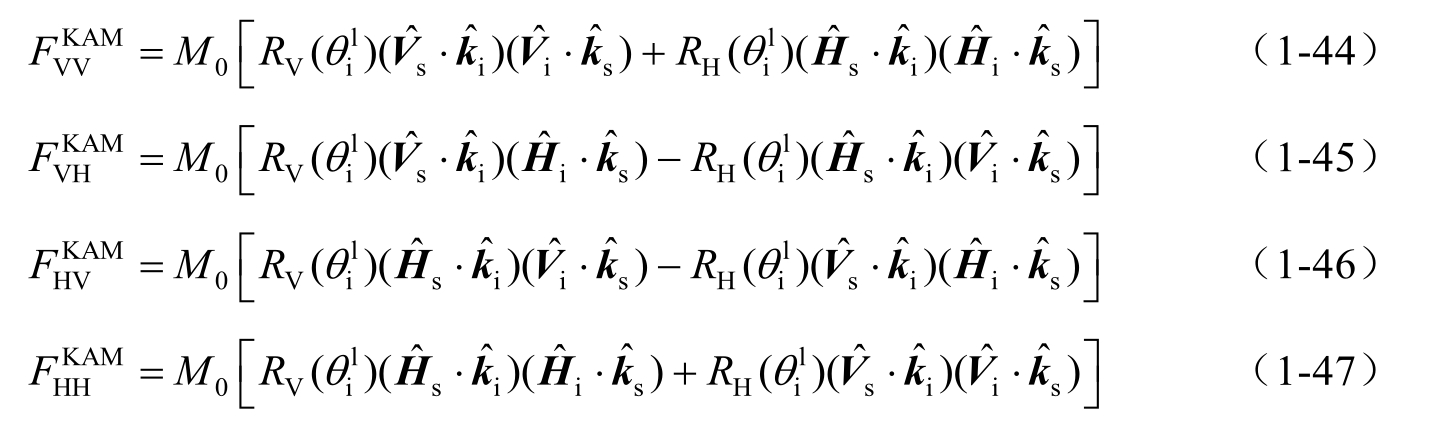
其中,
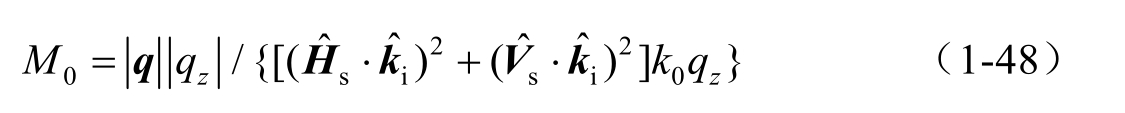
P ( z' x , z ' y )表示海面重力波的斜率概率密度函数,此处,
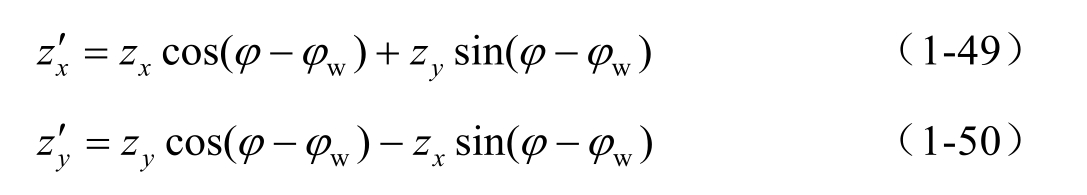
分别表示为主风向和侧风向的斜率, z x 、 z y 表示入射波镜像点处近似切平面的斜率:

Cox和Munk通过光学实验,认为海面斜率呈准高斯分布,可用四阶Gram-Charlier级数近似表示 [39] :
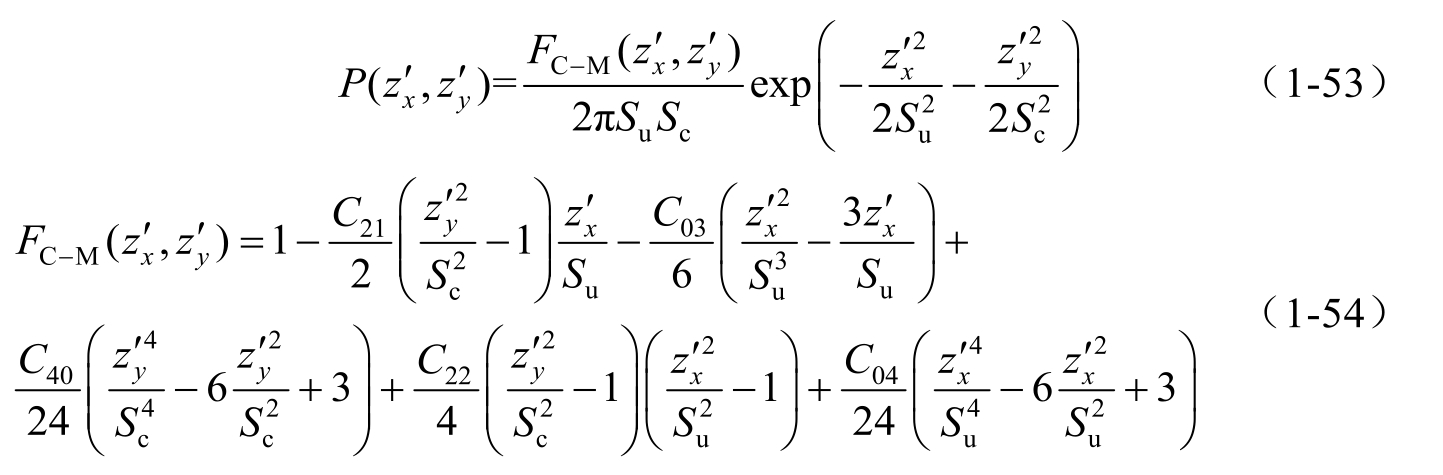
其中,
C
21
=0.01-0.0086
U
w12.5
±0.03和
C
03
=0.04-0.033
U
w12.5
±0.12表示海面斜率偏度,
C
40
=0.4±0.23,
C
22
=0.12±0.06和
C
04
=0.23±0.41表示海面斜率峰值系数,
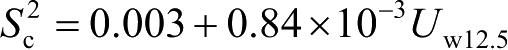 和
和
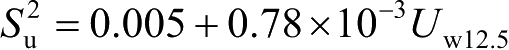 分别表示侧风和迎风方向的海面均方斜率。
分别表示侧风和迎风方向的海面均方斜率。
对式(1-41)和式(1-43)的散射系数进行叠加并按总面积归一化,可求得海面的总散射系数:
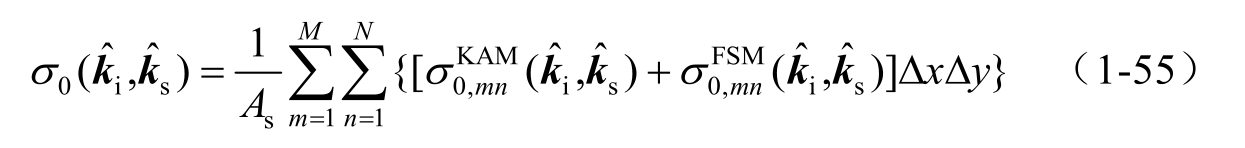
式中, A s = L x L y 表示海面场景的面积。
首先对半确定面元散射模型(SDFSM)的后向散射计算精度进行验证。图1-16给出了各极化条件下SDFSM的海面后向散射系数随入射角的变化情况。入射电磁波频率为14.9GHz,方位角为0°,迎风观测。图1-16(a)和(b)中风速分别为5m/s和10m/s。图中不同风速和极化的预估曲线与实测结果吻合较好,最大差值出现在垂直入射的镜像区,差值约为2.5dB。实验观测中3dB以内的误差是可以接受的。交叉极化结果由于幅值较小,且可获得的实测数据较少,这里不做讨论。
图1-17给出了不同入射方向、不同极化条件下,SDFSM的海面后向散射系数随风速的变化情况。入射电磁波频率为13.9GHz。图中离散点表示SEASAT-A卫星散射计实测数据 [41 ] 。图1-17(a)和(b)分别对应VV极化下,入射角30°和50°的情况,图1-17(c)和(d)分别对应HH极化下的对应结果。图中可以发现,在中等角度下,海面后向散射系数会随着风速的增大而增大。迎风预估结果略大于侧风情况。SDFSM 预估结果与实测数据大致吻合,主要差距出现在 HH 极化下,尤其是高海情条件下,HH 极化预估值明显小于实测值。在高海情掠射角条件下,线性海浪模型与复合散射理论无法解释海尖峰(Sea spike)现象,但在风速10m/s以下各预估曲线均处于实测范围内,而海洋尾迹特征只在中低海情(海面风速小于8m/s)中可观测到。因此,SDFSM可以很好地应用于海洋目标尾迹的电磁散射预估。
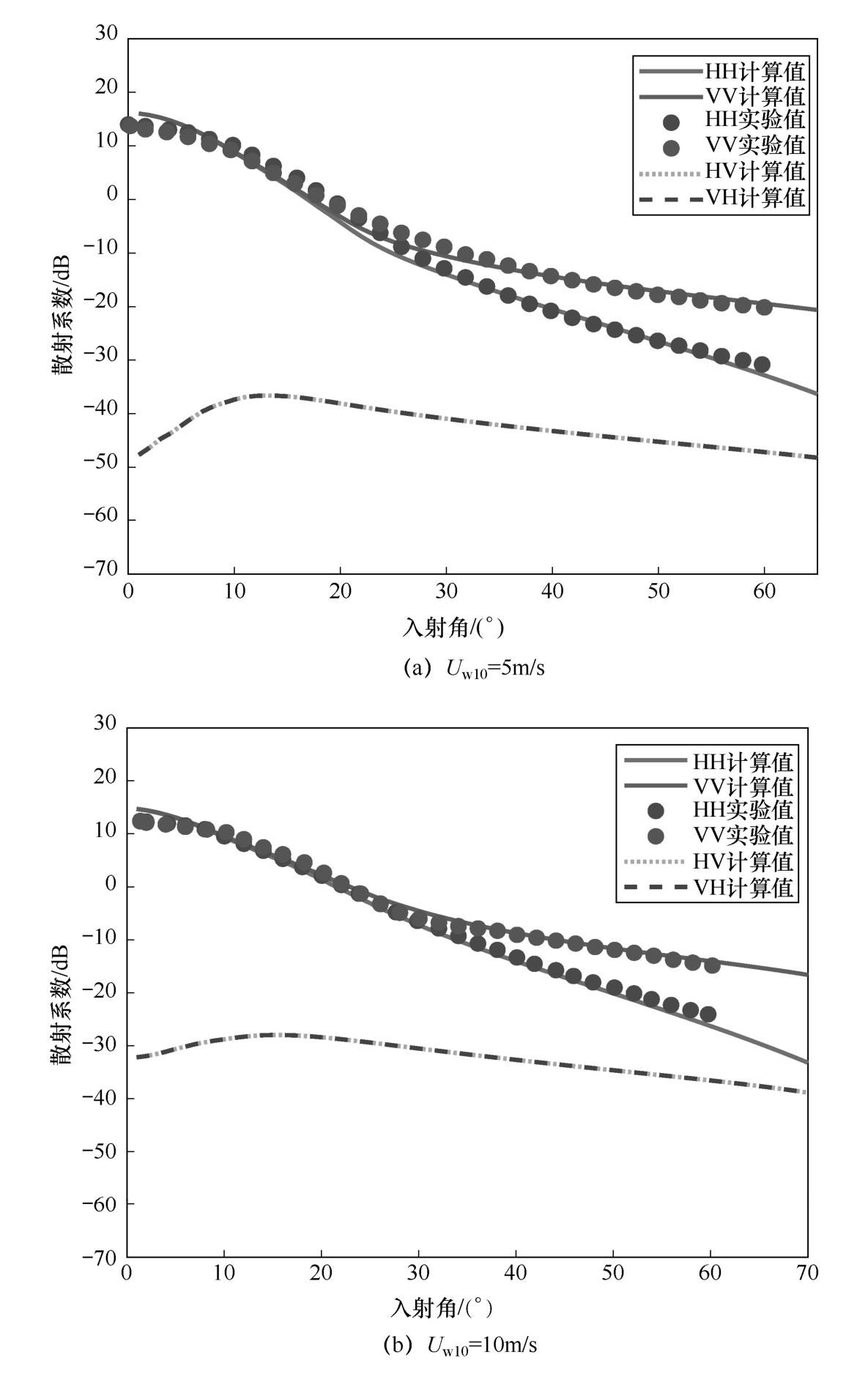
图1-16 各极化条件下SDFSM的海面后向散射系数随入射角的变化情况
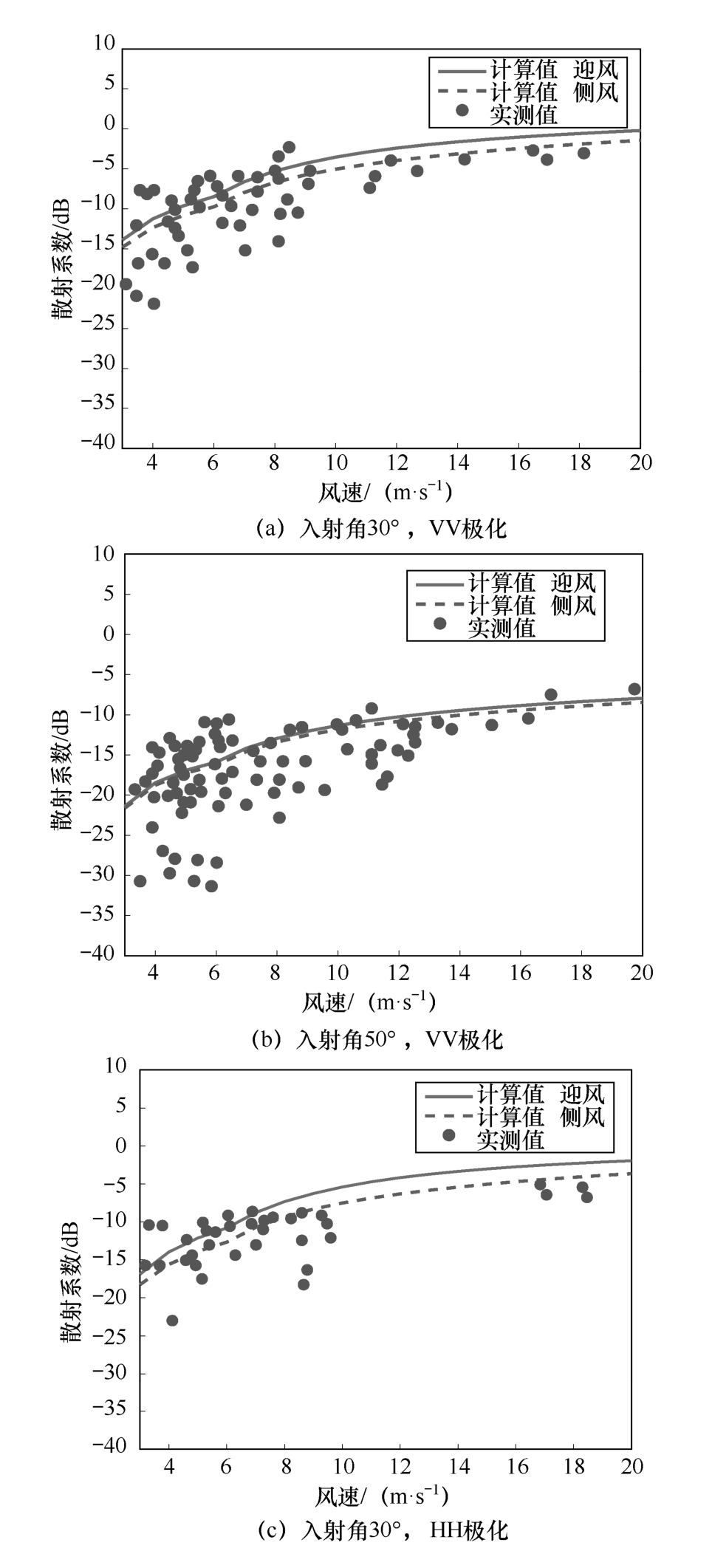
图1-17 不同入射方向、不同极化条件下SDFSM的海面后向散射系数随风速的变化情况
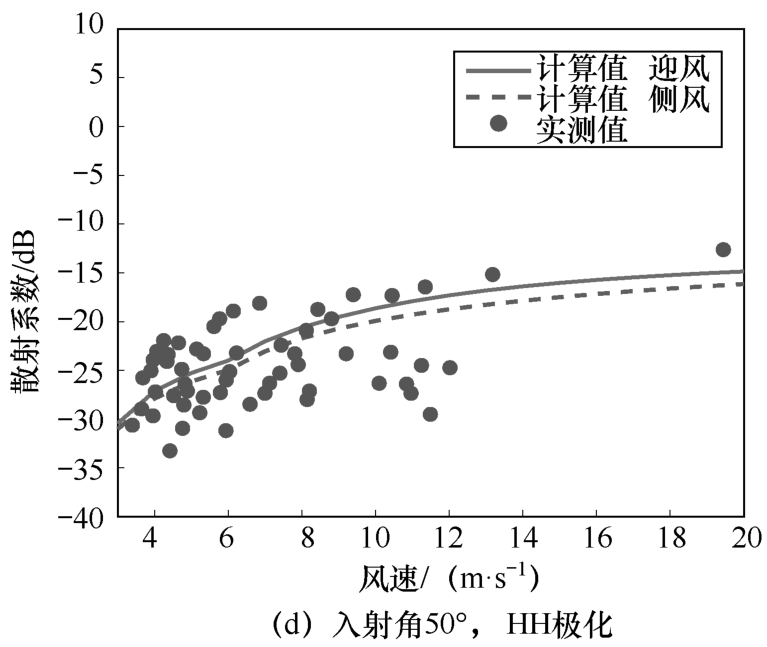
图1-17 不同入射方向、不同极化条件下SDFSM的海面后向散射系数随风速的变化情况(续)
图1-18(a)和(b)中分别使用SDFSM计算了海面单站和双站散射系数,并给出对应的KAM和SPM分量,用以说明海面复合散射理论各散射分量的贡献。以VV极化为例,电磁波工作频率为10GHz,单站散射情况下的入射角为0°~80°,双站情况下入射角为50°。可以看到后向散射镜向分量主要在入射角20°以内,当入射角大于30°时以Bragg散射为主。而双站散射镜向分量主要出现在入射角前向方向,后向方向主要以Bragg散射为主。
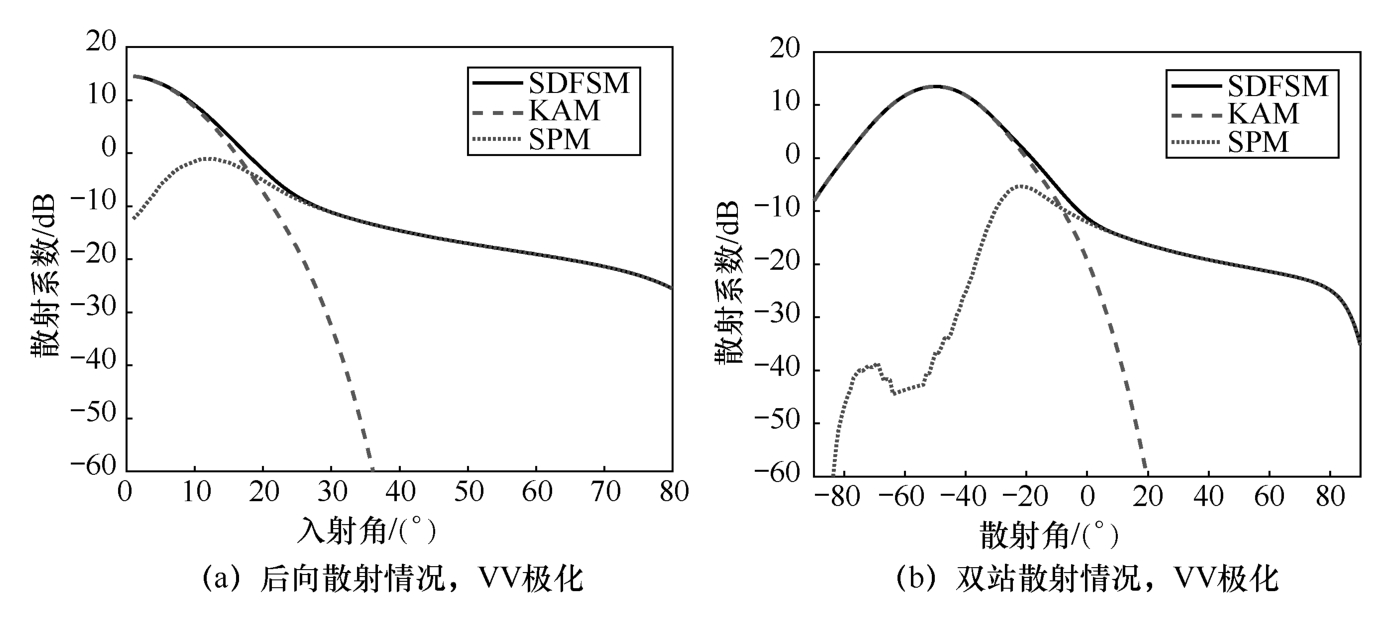
图1-18 海面单、双站散射镜向分量与Bragg散射分量分析