1.3 序贯均衡

纳什均衡的原始定义适用于具有完全信息的静态博弈，在不完美信息的动态博弈下可能存在不可置信的威胁。序贯均衡是对纳什均衡的严格而有影响力的改进，能够剔除不可置信的威胁，甚至被认为是对完美贝叶斯均衡的再精炼。

在博弈 G 中，参与者 p _i 的信念 β _i 表示对于每个信息集 I _ij 上的具体节点 x ∈ I _ij ，该参与者对其在该节点的概率判断为 β _i ( x )=Pr[ x | I _ij ]。信念系统 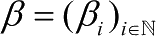表示每个参与者信念的集合，意味着参与者对处于信息集上的具体非终止节点的概率分布判断，即参与者对于其他参与者历史行为的判断。参与者在非终止节点 x 的期望效用 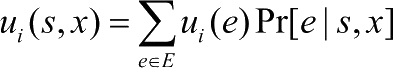表示该参与者从节点 x 到每个终止节点的概率与效用乘积之和，其中， u _i ( e )表示参与者在每个终止节点的效用，Pr[ e | s , x ]表示参与者到达终止节点的概率， s 表示策略组合。 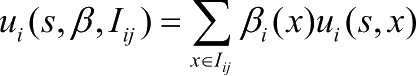表示该参与者在属于该信息集 I _ij 上的每个非终止节点的期望效用之和。

在博弈 G 中，给定策略组合s和信念系统 β 。如果对于任意参与者 p _i ，有∀ s _i＇ ≠ s _i , u _i (( s _i＇ , s _-i ), β , I _ij )≤ u _i ( s , β , I _ij )，则称 s =( s _i , s _-i )在信息集 I _ij 上是理性的。如果 s =( s _i , s _-i )在任意信息集 I _ij ∈ I 上都是理性的，则称( s , β ）是序贯理性的。如果存在一个完全混合策略组合序列 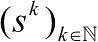收敛于 s ，以及通过贝叶斯法则得到的信念序列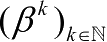（ 收敛于 β ，则称( s , β ）是序贯一致的。( s , β ）是序贯均衡的，当且仅当其是序贯理性且序贯一致的。也就是说，序贯均衡要求参与者的效用不止在整个博弈中是最优的，同时在每个信息集上都是最优的。 1lNRNH9Im4zJtfNfCZYQzGjVxKaqA8g/gAwEpg2Y37BPXpgVl65uUkE1/84IMydP