




在《密西西比河上的生活》这本书的开篇,马克·吐温提供了一直以来人们非常好奇的关于密西西比河的统计数据:长度为4 300英里,它的集水面积为125万平方英里,年储水量高达4.06亿吨。吐温经过计算发现:“如果把这条河里的泥浆收集起来,可以堆成一个面积为1平方英里、高241英尺的土方块。”书中的这部分内容都是非常经验主义的,甚至可以说有点枯燥乏味,尤其是对马克·吐温这样一个时而被称赞为幽默大师、时而因为亵渎神明而作品被禁的作家来说。
不过,吐温的各位粉丝不必担心!正如他自己所说:“了解事实以后,你就可以随心所欲地歪曲它们了。”像吐温这样技艺精湛的艺术家,可以利用一切线索,包括数字,编造出荒诞不经的故事,看看他的原话吧:
从某种意义上来说,这些枯燥的细节是很重要的。它们让我有机会介绍密西西比河最奇特的特点之一,那就是它的长度正在随着时间的推移而不断缩短。
和所有古老的河流一样,密西西比河的河道非常蜿蜒曲折。举个例子,直线距离只有675英里的河段,沿着河流的话要走1 300英里。不过有时候,由于河道太窄,河水会“跳”出河道的束缚,涌上地面,裁弯取直,使弯道变成直道。“不止一次,”吐温说,“它一跳,就把自己缩短了30英里!”在吐温的书出版前的200年间,密西西比河下游,也就是流经伊利诺伊州开罗市和路易斯安那州新奥尔良市之间的那一段,长度从1 215英里缩短到1 180英里,再缩短到1 040英里,最后缩短到973英里。
从这里开始,故事的走向就由马克·吐温操纵了:
在地质学中,这样的讨论机会和精确的数据简直可以说是绝无仅有的……请看下面:
在176年的时间里,密西西比河下游的河道长度缩短了242英里,平均每年缩短11/3英里。因此,任何一个具备冷静思考能力的人,只要不是瞎子和白痴,都能推测出,在志留纪时代,也就是100万年前的下一个11月,密西西比河的下游应该有130万英里长,就像一根钓鱼竿横亘在墨西哥湾上。同样,我们还可以推测,再过742年,密西西比河将只剩下不到1 41英里长。那时候,开罗市和新奥尔良市的街道将交会在一起,两个城市各有一个市长,在同一个市议员委员会的领导下慢吞吞地发展。这大概就是科学的迷人之处:只要稍微投资一些事实和数据,便能获得如此大的推测回报。
因此,马克·吐温只是在玩一个愚蠢的算术游戏吗?当然不是了!他研究的是一种深奥的几何游戏,其中涉及的几何元素是微积分的核心,是导数的安身立命之本,是一种普通的几何形状,即直线。
请仔细观察:
现在让我们来制作一个图表,用于描述历史上不同时期密西西比河下游(从开罗到新奥尔良)河道的长度:
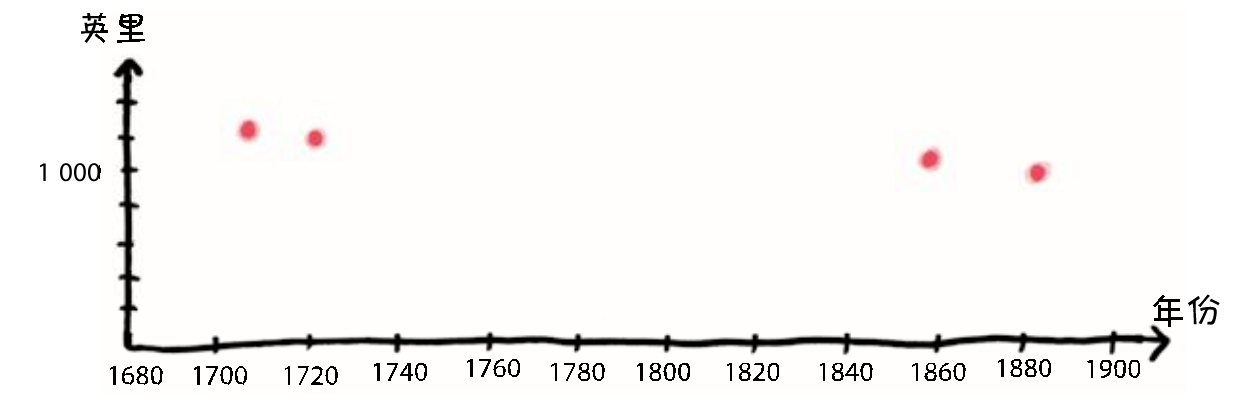
好吧,我们的数据的确少了点儿,但从图表中还是可以清楚地看出河流长度下降的趋势。近年来,统计学家们都热衷于用一种方法来修饰这种图表:一种被经济学家、流行病学家和草率的泛论者称为“线性回归”的分析方法。
首先,我们找到了图表的“中心点”。它的坐标很容易获得,就是现有数据坐标的平均值。
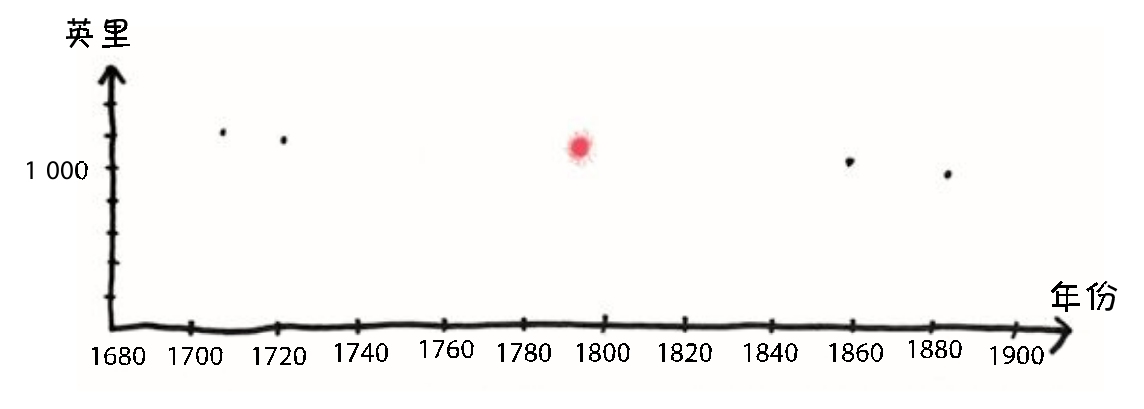
然后,从所有经过这一点的直线中,我们选择最接近所有数据的一条,也就是那条最接近所有已确认的点的直线。
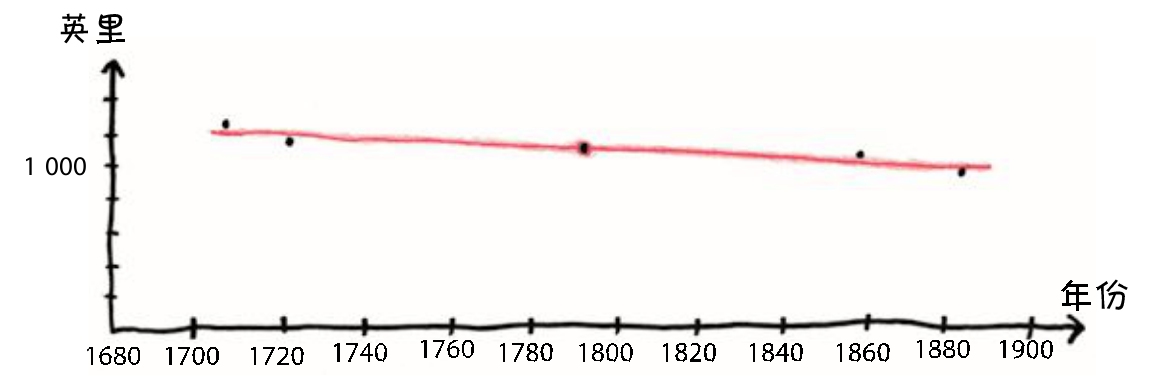
看哪!现在,我们的图像已经从几个零散的点——顽固、静止的小东西——一跃成为一条宏伟而连续的直线。它由 无数个 点组成,并且可以向任意方向延伸。
例如,我们可以把这条线延伸到遥远的过去:
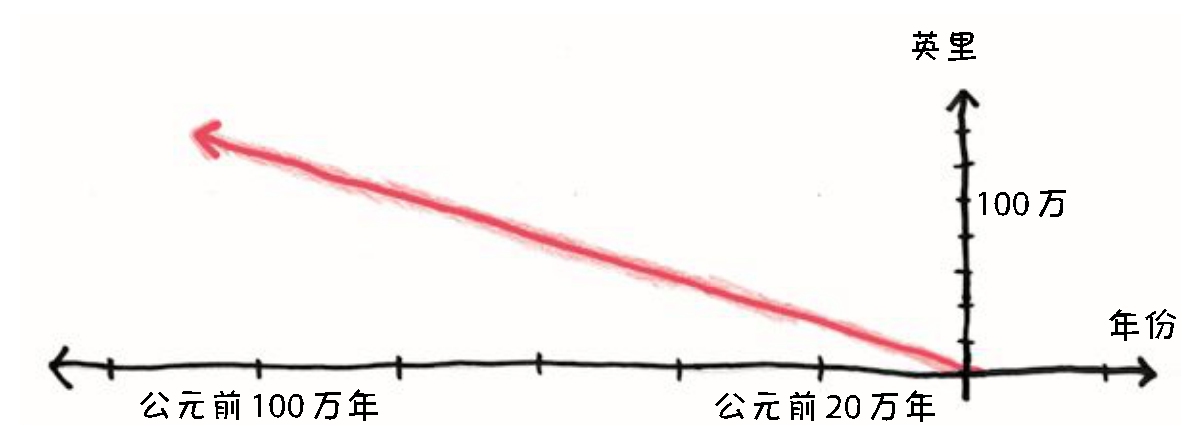
再看看!100万年前,密西西比河是一个宇宙级的庞然大物,长度超过100万英里。马克·吐温将其比喻为横亘在墨西哥湾上空的“鱼竿”实在太保守了,也不准确。经计算, “真正” 的密西西比河的长度大约是月球与地球之间距离的五倍。每当这颗“石头卫星”经过密西西比河上空时,河水就会像消防水带一样把它的月光浇灭。
由于直线有两个方向,我们还可以将线性模型向前推进:
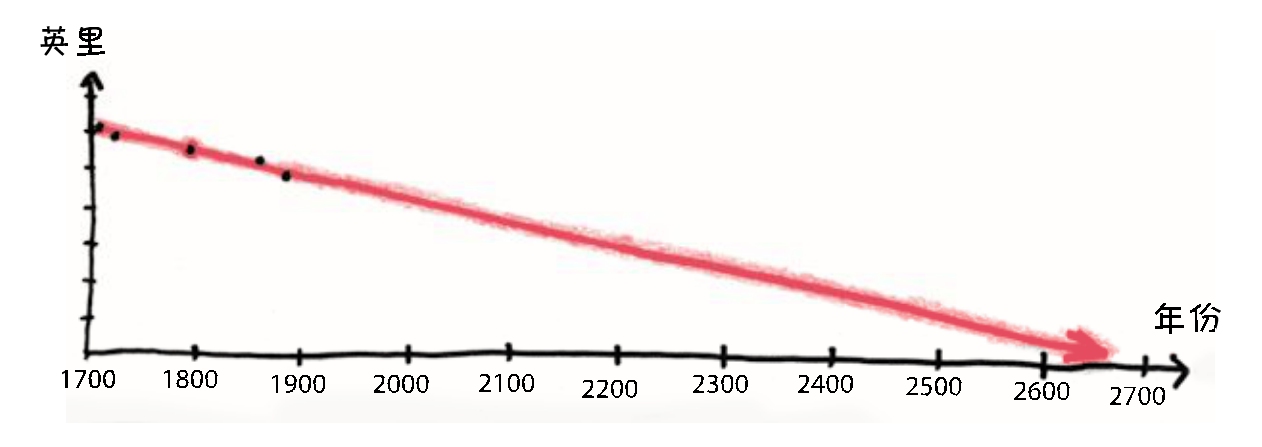
你明白了吧?图像显示,在28世纪即将到来之际,密西西比河的长度将缩减到不足1英里。为了实现这个目标,整个北美大陆将会像纸团一样被揉成一团,这使开罗和新奥尔良的市民成为他们期待已久的沿河邻居。此外,这两个城市之间还将出现一个500英里深、直通地幔的裂缝。
我听到你的嘀咕声了。你说:“任何严肃的数学,都不可能建立在这样经不起推敲的基础之上,因为这些数据本来就不可靠。”
嘿,你认为什么是“严肃的”数学?数学本来就是个逻辑游戏,既抽象(或许)又无聊。而在许多游戏中,直线都是不可或缺的简化工具,它能帮我们绕过冗长的计算弯路,就像河道的裁弯取直一样把时间缩短。因此,直线的身影随处可见:在统计模型中,在高维变换中,在奇异的几何曲面中,以及最重要的,在导数的核心中。
以抛物线为例。如果你的视力像老鹰一样敏锐,请睁大双眼盯着下面这幅图,你将会看到一个深刻而微妙的真理:抛物线不是一条线。
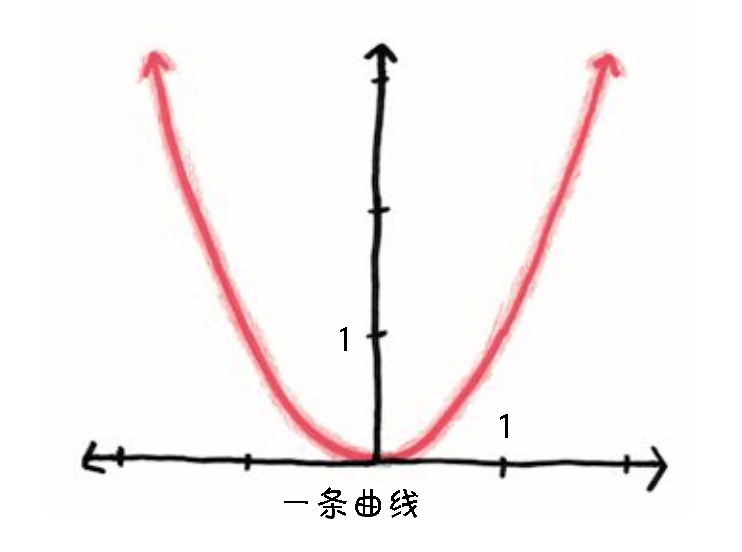
不好意思,我这样说不够准确,更确切地说,抛物线是一条曲线。但是,我们放大来看看。你现在看到了什么?
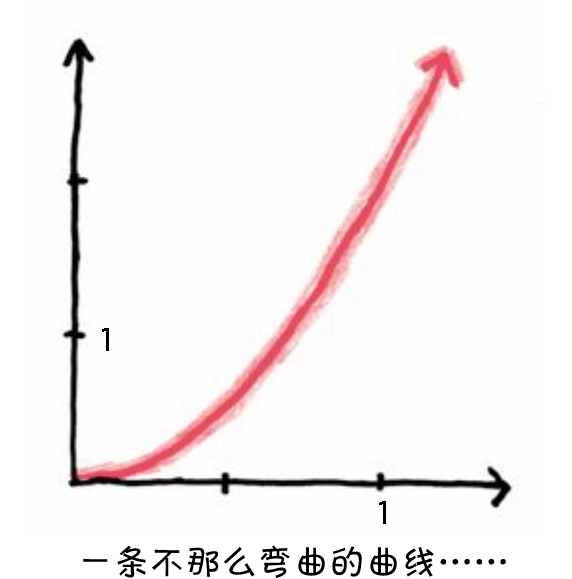
仍然是曲线,是的。但它是一条不那么弯曲的曲线,一个不那么像抛物线的抛物线。继续放大观察,会发现什么?

曲线逐渐变得平缓,曲度渐渐变得柔和,仿佛我们正哄着它慢慢进入梦乡。如果放大到足够近,曲线的曲率会变得非常微小,肉眼几乎无法分辨。严格来说,它仍然是一条曲线;然而,在实际计算中,为了计算方便,它最好是直的。
在某个无穷小的比例下——比所有已知的比例都小,但又没有达到零——这条曲线达到了我们想要的效果。至少在我们的想象中,它变成了真正的线性。
那么,这些和导数又有什么关系呢?它们之间的关系密不可分。
你可能还记得,导数就是特定时刻的变化率。例如,它可以告诉我们密西西比河的长度在“现在”这个精确瞬间是如何变化的。
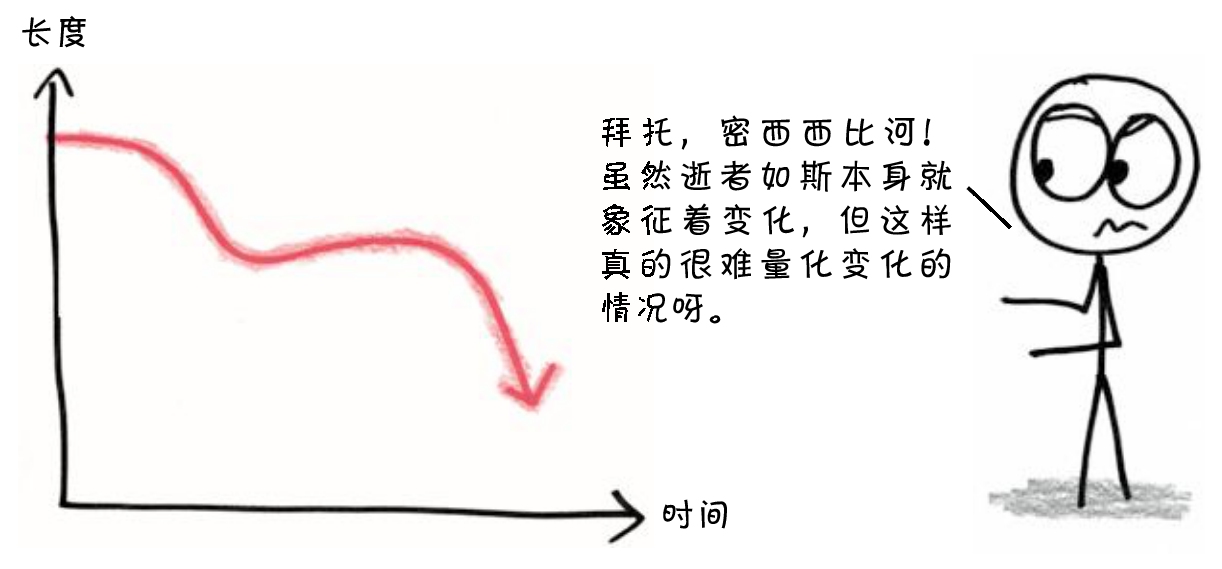
这个过程非常简单,我们可以把河流长度随时间变化的变化曲线放大,就像刚才对抛物线做的那样。如果放大到足够近,曲线被截取成无穷小的一段,线条的曲率会变直,这样我们就能求出导数了。
因此,所有的微分学都建立在一个简单的观察方法上: 放大,然后线性化。
当把地球按比例缩小来看时,地球的表面不是平的,因为它是个球体。如果我们试图把它夷为平地,只能绝望地发现自己得到的是像墨卡托投影那样扭曲的平面,而在这样的平面上,格陵兰岛(不到100万平方英里)看起来和非洲(近1 200万平方英里)一样大。但如果把地球放大来看呢?嘿,只要放大到足够近,你就永远不会注意到地平面的曲率。假如我想沿着密西西比河从伊利诺伊州的开罗到肯塔基州的哥伦布——一段20英里长的路程,只有地球周长的0.08%——只需要一张平面地图就足够了。
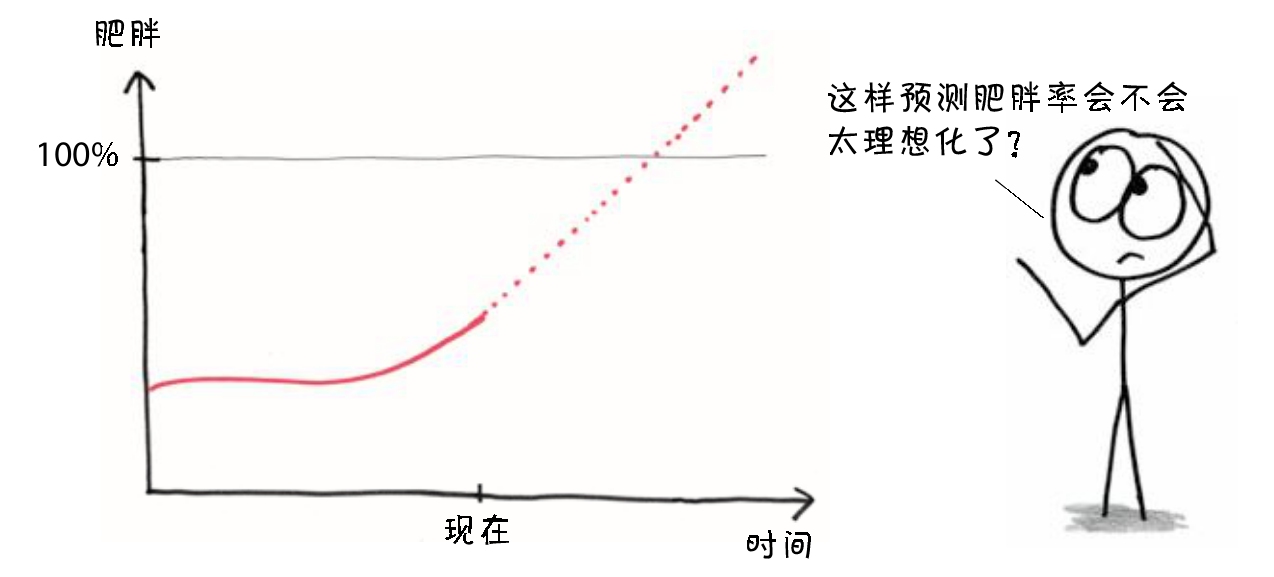
吐温犯了一个经典的错误,把变化曲线中 局部的 线性当成了 整体的 线性,因而得出的推测是荒谬的。他和我们开了个玩笑,但有人却一本正经地掉进了同样的陷阱而不自知。在《魔鬼数学:大数据时代,数学思维的力量》( How Not to Be Wrong: The Power of Mathematical Thinking )一书中(本章的许多想法都是我从这本书里“窃取”来的),文笔犀利的乔丹·艾伦伯格(Jordan Ellenberg)引用了一个教科书级别的错误示范:2008年,《肥胖》杂志上的一篇文章称,到2048年,美国成年人超重或肥胖的比例将达到,噔噔噔,100%。
可以想象,写这篇文章的研究人员把他们的线性模型扩展得太远了,已经随着地球表面的弯曲进入了太空。
类似的研究案例还有一个。2004年,《自然》杂志上发表了一篇简短的文章,指出奥运会女子100米短跑的成绩比男子提高得更快。“如果按照目前的趋势继续下去,”作者写道,“到2156年奥运会,女子100米短跑的成绩将会超过男子,届时男女选手都将在8秒之内完成比赛。”
可惜的是,等到2156年,奥运会在巴黎太空城、纽约月球城或谷歌人民共和国举行时,恐怕“当前的趋势”将不复存在。这是因为“当前的趋势”总是线性的,而历史上的变化曲线几乎都是非线性的。假设用同样的线性模型逆推古希腊,古希腊的勇士们则要用40秒的时间才能跑完100米——这是步行就能达到的速度,而最近路易斯安那州的一个101岁的老太太也能走这么快。如果用线性模型对未来进行预测,结果看起来就更奇怪了:随着百米夺金所用时间的不断缩短,未来人类奔跑的速度将达到电影《星际迷航》中飞船飞行的速度。
生命就像密西西比河,蜿蜒地前行。将它放大到一定程度后,你可能会发现一段直线,但整个生命的历程是永不停歇和九曲十八弯的。
在本章即将结束之际,我还想分享一下《密西西比河上的生活》的最后一段,是关于密西西比河三角洲的:
随着河流中泥沙的沉积,陆地缓慢地延伸了,但只是缓慢地(在过去的200年里,只延伸了不到1/3英里)……科学家们认为,过去密西西比河的河口在巴吞鲁日,也就是群山的尽头,从那里到墨西哥湾之间的200英里长的平原是由河流沉积作用形成的。我们国家这一部分的历史就发迹于此,毫无疑问,这是整整12万年的历史。
这是另一个关于线性模型的案例。马克·吐温这次将视角转向了最近200年
 。在地质学中,200年不过是一刹那,在此期间,陆地的面积增长了1/3英里(约以每年9英尺的速度)。于是,马克·吐温逆推后认为,在12万年前,密西西比河三角洲位于目前密西西比河上游200英里处。
。在地质学中,200年不过是一刹那,在此期间,陆地的面积增长了1/3英里(约以每年9英尺的速度)。于是,马克·吐温逆推后认为,在12万年前,密西西比河三角洲位于目前密西西比河上游200英里处。
唉,马克·吐温还是犯了与《肥胖》杂志上的那篇文章的研究人员同样的错误,明明他在书中的其他地方还曾嘲讽过这个错误。
正如我们所知道的,密西西比河的历史可以追溯到上一个冰河时代的末期,也就是1万年前。而马克·吐温的线性模型却向过去延伸了100万年,这就如同将一条河流延伸到太空深处。他试图用一个导数来描述所有的永恒,却忘记了它只能表达那一个瞬间的变化。
第6个瞬间
夏洛克·福尔摩斯在运动学上犯了难。