




我一直都热衷于创造一些数学名词。成不成功另说吧,但至少我总是跃跃欲试。不过现实总是残酷的,时至今日,我创造的“抵消乐”(canceltharsis,用于描述成功在等式两边消去一个相同项带来的满足感)和“代数怒”(algebrage,用于描述因为一个小小的代数错误而耗费好几个小时的愤怒)还没有真正流行起来。唉,这也从另一个角度说明了戈特弗里德·莱布尼茨的成就确实远在我之上,因为他创造了很多数学名词,比如:
不仅如此,他还创造了很多后来广为流传的数学符号,例如,用“≌”表示全等,用“=”表示比例,用“()”表示运算时的优先顺序。众所周知,我们现在所用的数学表达方式都构建在莱布尼茨于17世纪开辟的大道上。然而,即便如此,以上的所有这些和他最伟大的贡献相比,也不过是个脚注而已。
没错,我说的正是字母“d”。
这一贡献听起来极为小儿科,简直是数学界的《芝麻街》
 水平。伟大的数学家迈克尔·阿蒂亚爵士(Sir Michael Atiyah)曾在2017年这样打趣道:“莱布尼茨所做的贡献,不过就是把d排在了
x
前面,显然,你也可以通过这种方式让自己名声大噪。”
水平。伟大的数学家迈克尔·阿蒂亚爵士(Sir Michael Atiyah)曾在2017年这样打趣道:“莱布尼茨所做的贡献,不过就是把d排在了
x
前面,显然,你也可以通过这种方式让自己名声大噪。”
实事求是地说,人类在数学符号上的突破在后人看来总是平平无奇的。你有没有感谢过罗伯特·雷科德(Robert Recorde)?由于他发明了等号“=”,我们不必再在数学表达中一遍又一遍地重复“等于”这个词。而发明数学符号的初衷就是让人们能简洁地将思想投射于纸上。当这些符号如此自然而流畅地跃然纸上时,你往往会忘记它们都是由人精心创造和挑选出来的。喂,别搞错了:数学符号可不是什么自然的产物,它是一项了不起的技术壮举,是大脑通过其他方式的延伸,就像机械手一样怪异,但影响深远。
纵观历史,没有人能像莱布尼茨那样,创造出如此清晰又生动的符号。“我怀疑莱布尼茨在数学上的成功,”计算机科学家斯蒂芬·沃尔夫拉姆(Stephen Wolfram)说,“在很大程度上归功于他对符号的投入。”
莱布尼茨出生于1646年,比牛顿小几岁。他既是一位哲学家,又是一个社会名流。肖像画中的莱布尼茨常常戴着彰显其尊贵身份的巨型假发,而“创立微积分”仅仅是他极为华丽的履历中的内容之一。莱布尼茨还是欧洲顶尖的地质学家,中国文化及棘手的法律案例方面的专家,一言以蔽之,他是欧洲最卓越的科学家之一。一位雇过莱布尼茨的王室成员曾感叹着称他为“我的活字典”。在莱布尼茨的一生中,他给1 000多名学者写了15 000封信。
他十分关心读者们是否能理解信中的内容。不像牛顿故意将《原理》写得晦涩难懂,莱布尼茨相当重视清晰的沟通。因此,在发展微积分的概念时,他会注意给它们穿上漂亮而合身的符号外衣。
例如,d这类符号。
在数学中,Δ(希腊字母“delta”)代表变化。设想一个摘自今天早上新闻头条的例子,而这件事在六个月前是闻所未闻的,那就是我去跑步啦。
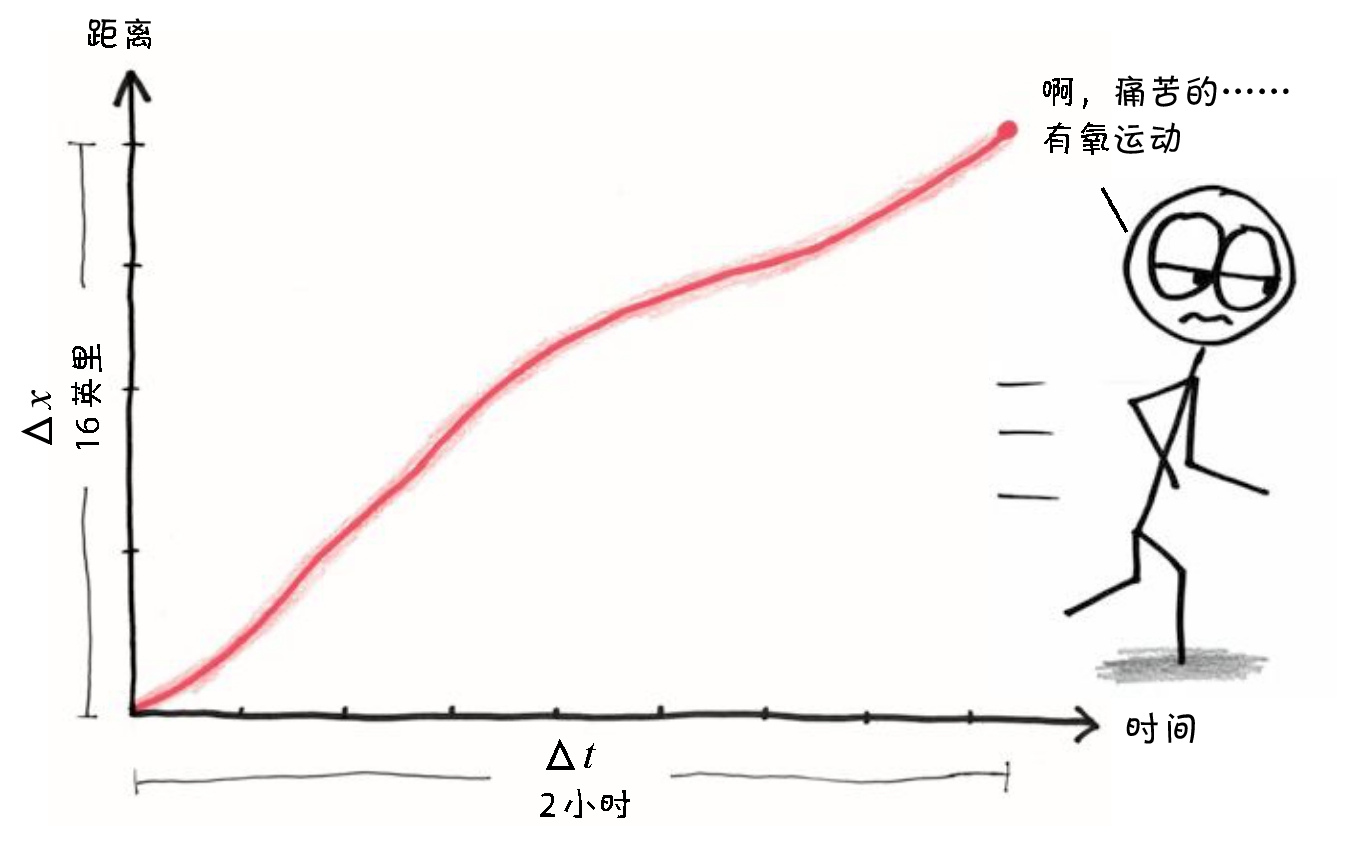
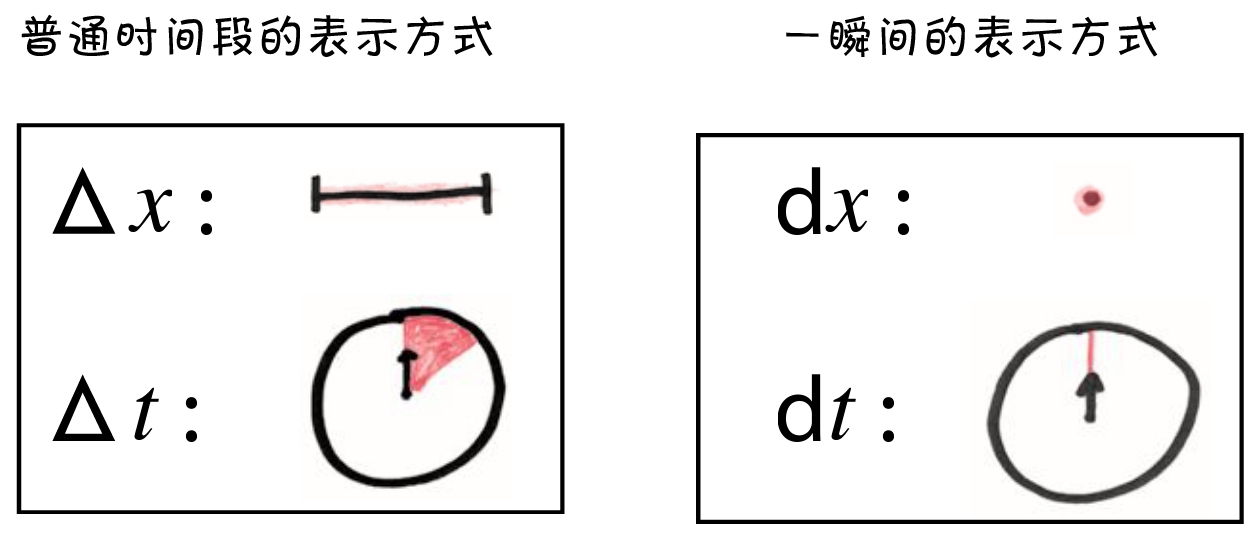
假设 x 是我离家的距离,那么Δ x 就是这个距离内的一小段变化量,比如说16英里(因为这是我的书,所以我吹个牛也没太大关系吧)。
现在,如果 t 是时间,那么Δ t 就是我跑步期间的某个时间段——让我们假设其为2个小时(嘿,因为这个数算起来更简单,不过这样看起来我就变成一个飞人了)。
那我跑步的速度是多少呢?显然,在计算任何变化速率的时候,我们都要用到除法。这里是用Δ x 除以Δ t ,得到的速度为8英里/时。
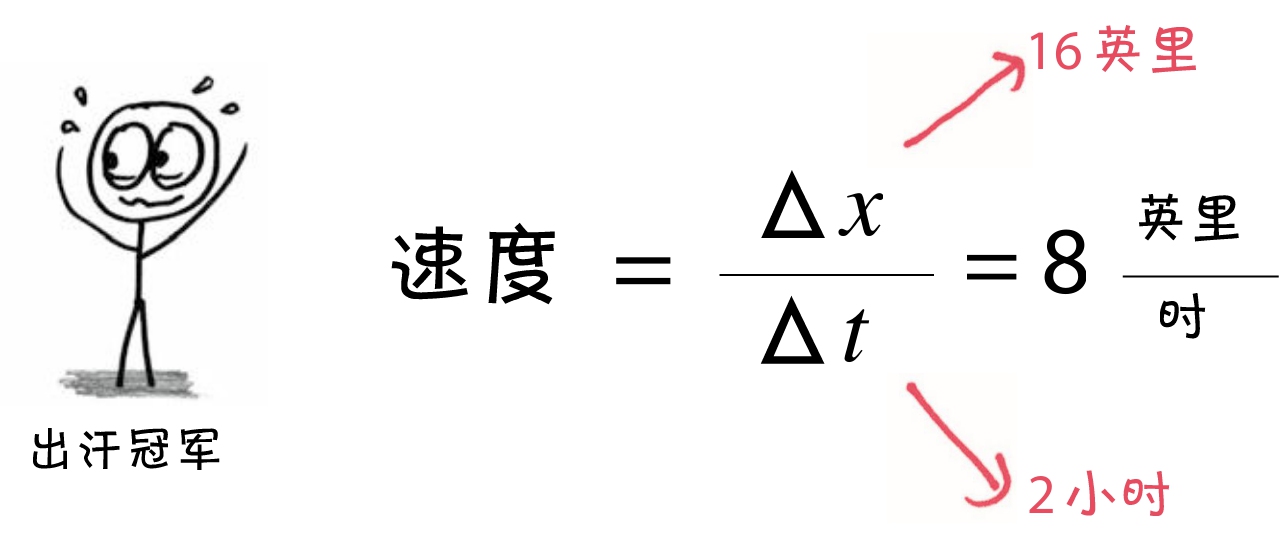
好了,我再问你,我下午1点时的跑步速度是多少?你可能还记得,导数表示的是瞬时变化率。它所分析的不是2小时的悠闲时间,而是将时间段无限放大,再聚焦于其中一个时间点,从而得到一个瞬时的定格画面。
不过,这就带来了一个问题,即在这个无穷小的瞬间里,既没有时间的流逝,也没有距离的变化,Δ x 和Δ t 均为零。而用0除以0是无法给出一个有意义的答案的。
噔噔噔,莱布尼茨的新符号登场了。现在,我们先放下Δ x 和Δ t ,来看看d x 和d t ,它们分别是位置和时间的无穷小增量。
在这里,莱布尼茨赋予导数的符号是:
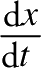 。
。
此处有一个“陷阱”:d x 和d t 并不是实际存在的数字,你没法真正地用它们进行除法运算。这两个符号另有深意,它们更像一个类比,也可以说像变魔术时的一个障眼法,而这正是符号的意义如此重要的原因。哈佛大学的数学家巴里·马祖尔(Barry Mazur)将莱布尼茨的导数比作来自中文等语言的半象形文字:它不是一个随意的符号,而是对概念本质的一个小小的提示性说明。他将导数列为自己“最喜欢的数学术语”之一,原因是“只要看一眼,它的意思便不言而喻”。
我必须承认,在学生时代,我更喜欢受牛顿影响的符号(这样的符号我们在第3章中见过)。对我来说,关于
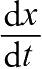 的一切感觉既混乱又复杂,而且最糟糕的是其中的陷阱:一个不算真正分数的分数。
的一切感觉既混乱又复杂,而且最糟糕的是其中的陷阱:一个不算真正分数的分数。
然而,随着时间的推移,我逐渐意识到莱布尼茨符号中“d”所具有的神秘力量:它太灵活了。普通的符号往往只能容纳单一的输入变量(通常是时间),而莱布尼茨的符号的容纳范围要广泛得多,让我们能在复杂的运算芭蕾舞中编排大量的变量。
想看看吗?那就跟着我一起走进经济学课堂,或者更有趣的叫法,一个玩具公司的会议室。
我们这家公司生产的产品是泰迪熊玩偶,获利的方式是以特定价格(
p
)卖出特定数量(
q
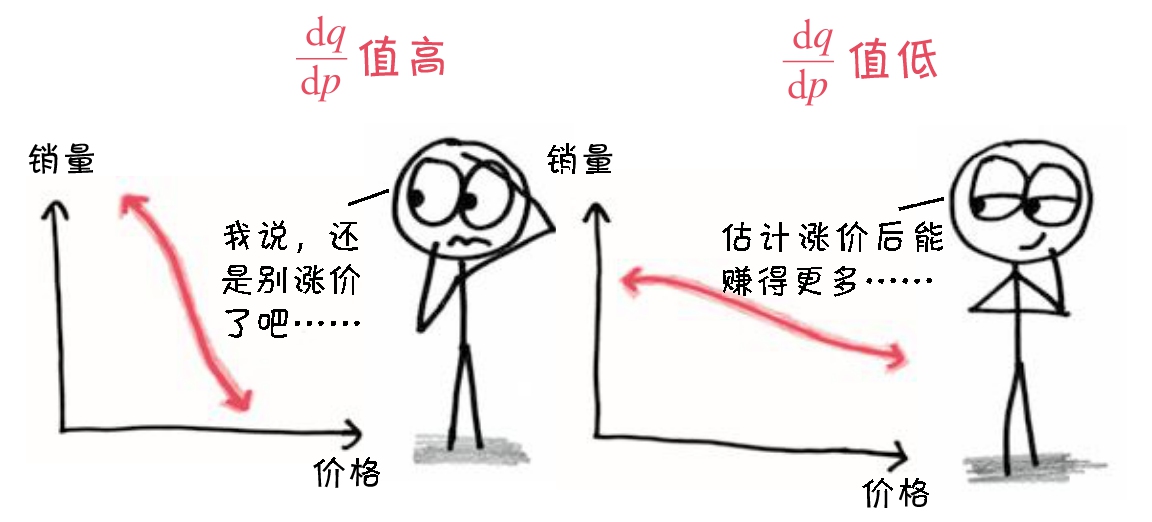
)的泰迪熊。如果我们将价格提高一点,会发生什么呢?笼统地说,泰迪熊的销量会减少,但更准确的答案要用导数来表示,即
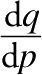 ,这是销量关于价格的瞬时变化率。
,这是销量关于价格的瞬时变化率。
另外,
q
的值不只取决于
p
的值。假设我们花
a
美元来做电视广告。在这种情况下,利用
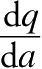 就可以算出额外的广告费对销售的边际效用。
就可以算出额外的广告费对销售的边际效用。

不过,如果我们做的广告比较多,可能就需要提高泰迪熊的价格了。这意味着要考虑
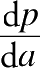 ,也就是广告费的变化对产品价格的影响。
,也就是广告费的变化对产品价格的影响。
我们甚至可以把导数上下颠倒过来,就成了
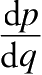 ,这是什么意思呢?它表示的是无穷小的
销量
变化对
产品价格
的影响。
,这是什么意思呢?它表示的是无穷小的
销量
变化对
产品价格
的影响。
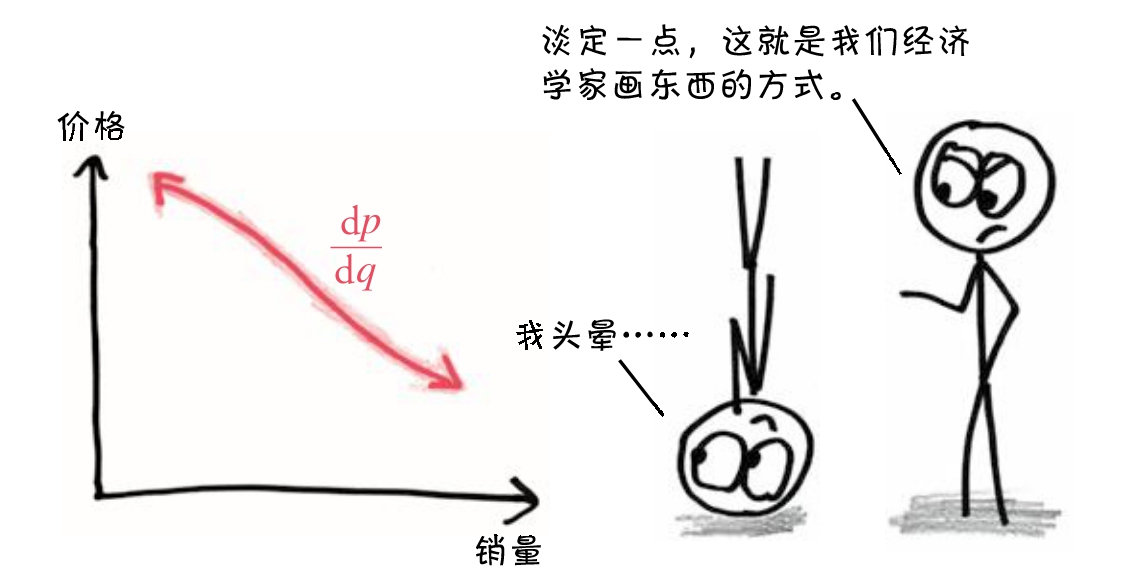
普通的符号能应付如此多样的导数吗?算了吧!只有灵活多变的莱布尼茨d家族才能如此优雅而巧妙地完成任务。正因为如此,莱布尼茨创造的符号对微积分的影响深远,并成为展现微积分的完美语言。
我不知道你是怎么想的,但我做泰迪熊玩偶的生意可不是为了交朋友,更不是为了削弱小孩子面对熊时无可指摘的恐惧而把食肉动物做成毛茸茸的可爱模样。我来这里就是为了赚钱,因此对我来说,输出变量只有一个,即利润。

为了使利润最大化,我们不想把价格定得太低。比如制作一只泰迪熊需要5美元;在这种情况下,以5美元的价格卖出一只泰迪熊是做慈善,而不是做生意。当然5.01美元也不太够——尽管在这个超低的折扣率下,我们可以卖出很多只泰迪熊,但就算卖出去100万只,我们也只能赚1万美元。

但是另一方面,我们也不想把价格定得太高。如果每只泰迪熊要价5 000美元,也许会有一个天真单纯的亿万富翁买一只回去,但更大的可能是根本不会有人想买。这样一来,销量就太低了,根本赚不到什么可观的利润。
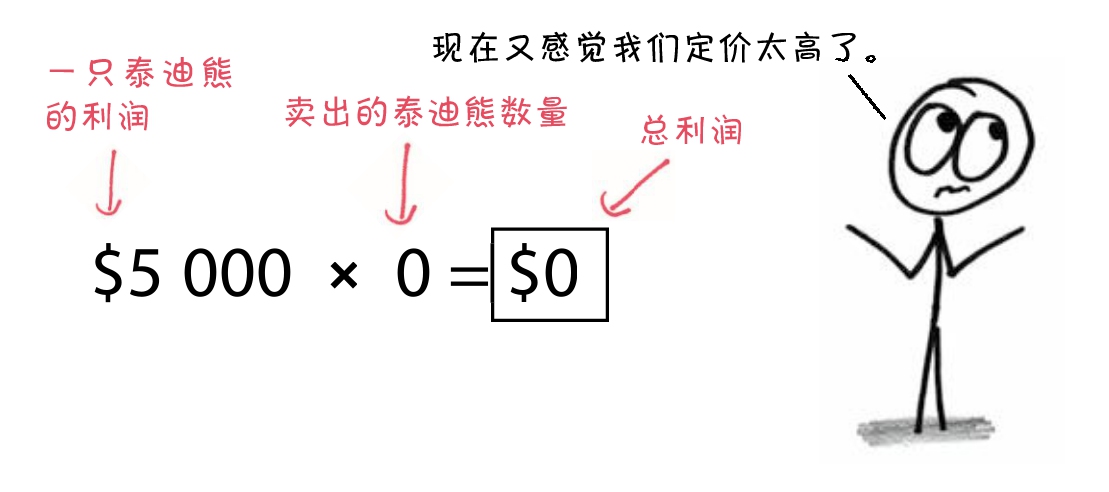
这时候,我们就需要用导数来定价格了,试求:如果我们将价格提高一个无穷小的增量,那将如何影响我们的利润?

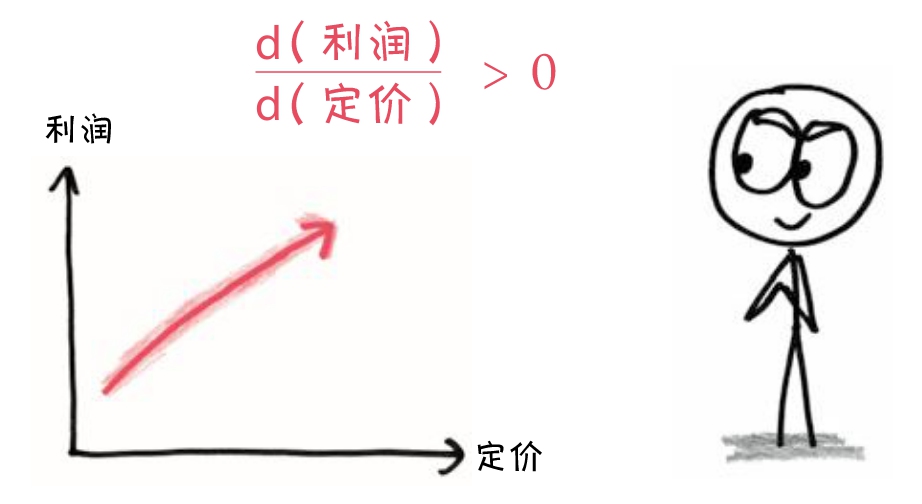
导数为正?这意味着提高价格会提高利润。换句话说,我们的定价过低了。
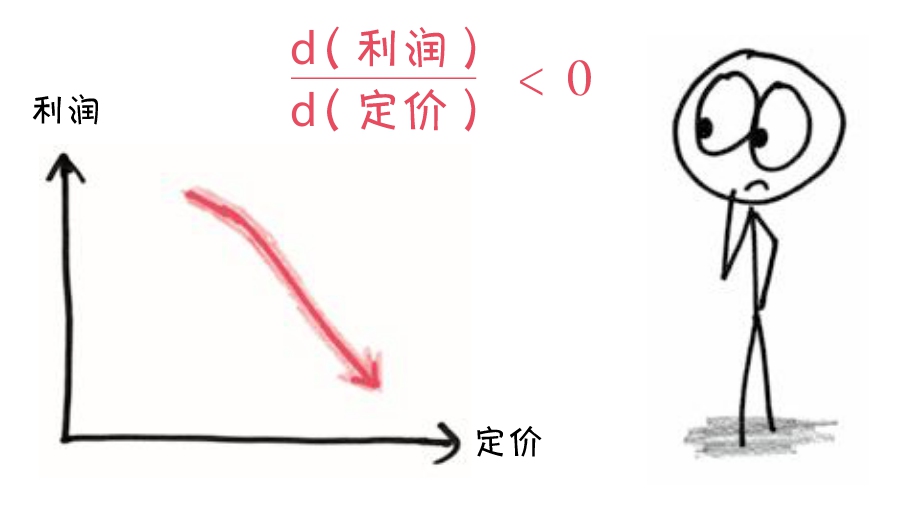
导数为负?这意味着降低价格会吸引更多顾客,从而提高利润。换句话说,我们的定价太高了。
我们要找到一个特殊的瞬间:导数恰好为零的价格。
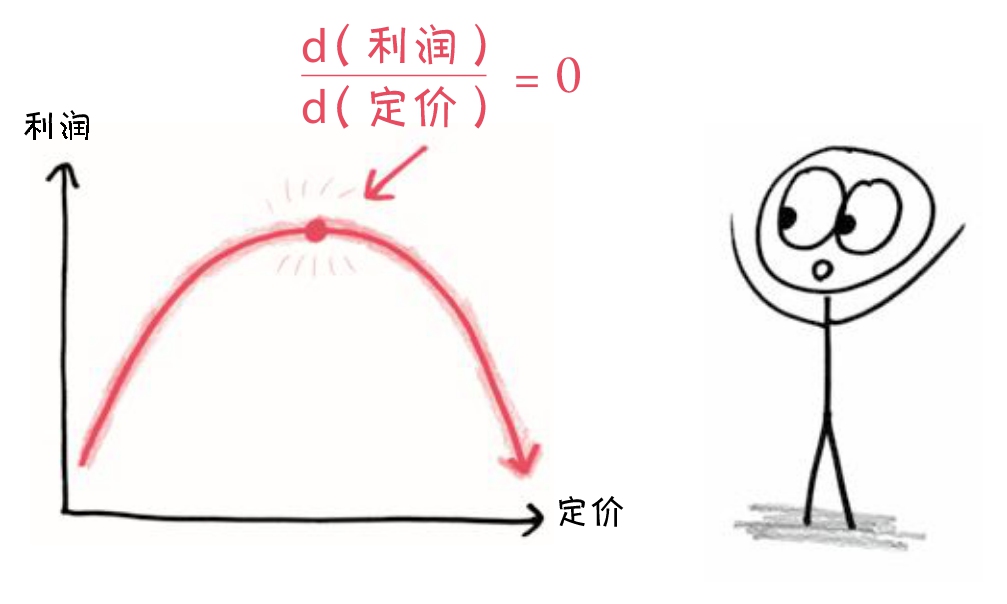
函数图像上的 “极大值” 是一个重要的转折点,此时导数从正数转换为负数。而 极小值 则正好相反,此时导数从负数变为正数。其中的逻辑其实很简单:朝一个方向坚持,直到事情不再变好,开始变糟为止。这便是我们能做到的最好情况。
不过,在我们的定义中,极大值不是就 总体 而言的(它并不是所有点中最高的),而是就 局部 而言。从这一点向左移动一根头发粗细的距离,曲线是向上倾斜的;向右移动一根头发粗细的距离,曲线是向下倾斜的;再看回这一点,导数为零。这就是在微观分析的基础上确定的极大值。这是一个非常实用的小技巧,就像通过土壤样本来识别山顶一样。
微积分历史上第一篇公开发表的论文是莱布尼茨的《一种求极大值与极小值和求切线的新方法》(“Nova Methodus pro Maximis et Minimis”),于1684年发表。数学家莱昂哈德·欧拉(Leonhard Euler)曾说:“世界上一切事情的意义都在于某个极大值或极小值。”
20岁出头时,莱布尼茨加入了一个排他性的炼金术士组织(嘿,那是17世纪60年代,人们对炼金术趋之若鹜)。为了证明自己对炼金术的忠诚,莱布尼茨整理了一份流行语大全,并荒谬地从中拼凑出一封堆砌辞藻、令人印象深刻的求职信。他这么做还真的管用:那些炼金术士眼前一亮,推选他做了该组织的秘书。不过,出人意料的是,莱布尼茨很快看透了他们的把戏。几个月后,他就离开了,并谴责该组织是“造金兄弟会”。
在我看来,这很莱布尼茨。进入一个领域后,首先你要做的是掌握这个领域的语言。接下来,真相,不管是什么样的真相,就会逐渐浮出水面。在学会炼金术士必备的花言巧语后不到十年,这个傲慢的年轻人发明了至今仍被无数人使用的数学词汇。
莱布尼茨有没有成功地把铅变成金子?并没有,但他完成了更重要的事:把小写的d变成了关于瞬间的永恒语言。

第5个瞬间
马克·吐温给我们上了一堂数学课。