下载掌阅APP，畅读海量书库
立即打开
在线性回归系数向量的解中，要求
X
T
X
可逆，实际上当
X
T
X
的条件数很大时，解的数值稳定性不好。一个矩阵的条件数为其最大特征值与最小特征值之比，设
X
T
X
的所有特征值记为{
λ
0
，
λ
1
，
λ
2
，…，
λ
K
}，若特征值是按从大到小排列的，则其条件数为
λ
0
/
λ
K
。矩阵
X
T
X
的行列式为
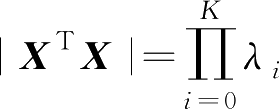，由于
X
T
X
是对称矩阵，其特征值
λ
i
≥0。若最小特征值
λ
K
=0则矩阵不可逆，若有一个到几个特征值很小，相应条件数很大，矩阵行列式值可能很小，根据矩阵求逆的格莱姆法则，则
X
T
X
的逆矩阵中有很多大的值，相应解向量可能范数很大且数值不稳定。
当 X 中的一些不同列互成比例时， X T X 不满秩，这时 X T X 不可逆。当 X 的一些列相互近似成比例时，对应大的条件数，尽管此时严格讲 X T X 可逆，但当计算精度受限时数值稳定性不好。从以上的分析可见， X 的不同列分别对应权系数向量的一个分量，当 X 的一些列成比例时，相当于对应的权系数有冗余，可以减少权系数数目，即减少模型的复杂性。当 X 的条件数很大时，相当于模型参数数目超过了必需的数目，而过多的参数其实更多地被用于拟合训练数据集中的噪声，使得泛化性能变差。因此， X T X 条件数很大，对应的是模型的过拟合。解决过拟合的基本方法，一是增加数据集规模，二是删除一些冗余变量及相应权系数，三是采用正则化。这里介绍正则化方法。
如第1章所引出的结论，所谓正则化是在用误差平方和表示的目标函数中增加一项约束参数向量自身的量，一种常用的约束量选择为参数向量的范数平方，即
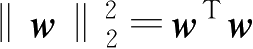，因此加了正则化约束的目标函数为
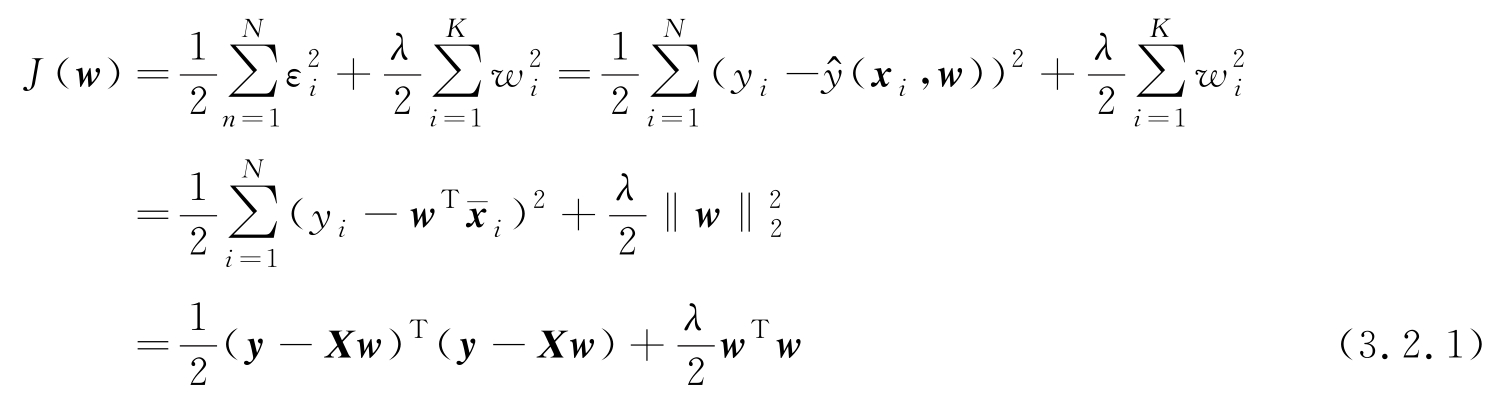
这里 λ 是一个可选择的参数，用于控制误差项与参数向量范数约束项的作用。为求使式（3.2.1）最小的 w 值，计算
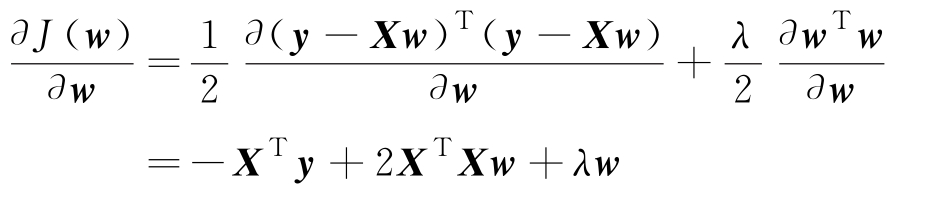
令 w = w R 时上式为0，得
求得参数向量的正则化解为
这里，解 w R 中用下标 R 表示正则化解。线性回归的正则化是一般性正则理论的一个特例。Tikhonov正则化理论的泛函由两部分组成：一项是经验代价函数，如式（3.1.11）中的误差平方和是一种经验代价函数，另一项是正则化项，它是约束系统结构的，在参数优化中用于约束参数向量的范数。每一种不同的正则化项代表设计的一种“偏爱”，例如权系数范数平方作为正则化项是一种对小范数的权系数的偏爱，这种正则化称为“权衰减”（weigh decay）。
例3.2.1 若给定一个数据集， X T X 的最大特征值为 λ max =1.0，最小特征值为 λ min =0.01，条件数 T = λ max / λ min =100。若正则化参数取 λ =0.1，则 X T X + λ I 的最大特征值和最小特征值分别为 λ max + λ =1.1和 λ min + λ =0.11，因此条件数变为 T R =1.1/0.11=10，对于线性回归来讲，正则化相当于改善了数据矩阵的条件数。
正如式（3.1.10）的误差平方和目标函数与最大似然等价，式（3.2.1）的正则化目标函数与贝叶斯框架下的MAP参数估计是等价的。若采用贝叶斯MAP估计，需要给出参数向量
w
的先验分布，假设
w
的各分量为均值为0、方差为
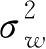且互相独立的高斯分布，则先验分布表示为
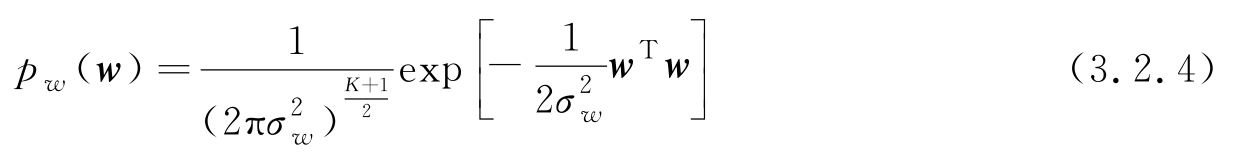
根据MAP估计，求 w 使得下式最大：
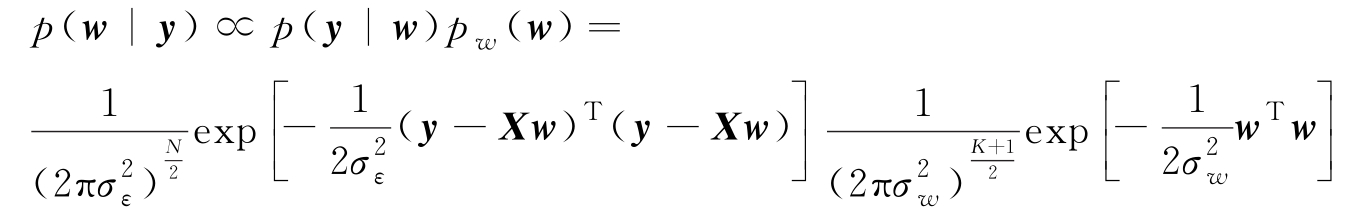
对上式取对数可知，求上式最大等价于求 w 使得下式最小：
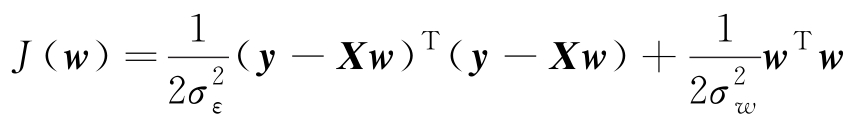
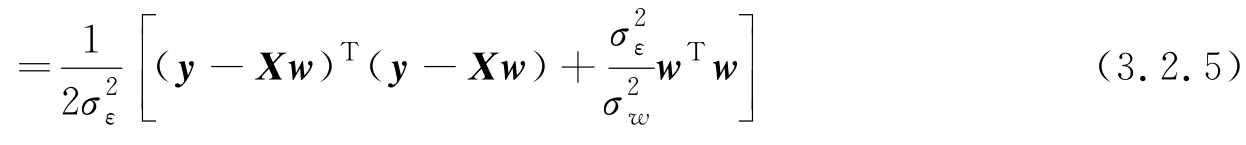
令
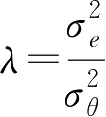，则式（3.2.5）中方括号内的内容与式（3.2.1）相同，其参数向量
w
的解为式（3.2.3）。因此，可将正则化线性回归中权系数向量的先验分布看作高斯分布下的贝叶斯MAP估计。
用式（3.2.1）第2行对 w 求导，不难得到相应于式（3.2.3）解的梯度递推算法，这里只给出小批量SGD算法如下：
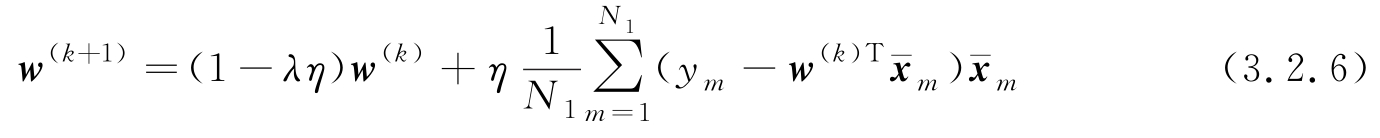
当取 N 1 =1时小批量退化成单样本SGD。与式（3.1.29）比，在 w （ k ） 前多了一个收缩因子（1- λη ），并增加了一个超参数 λ 。
这里可以得到一个基本的结论，若一类机器学习算法的目标函数是通过最大似然得到的，则任何一种对权系数向量施加先验分布 p w （ w ），从而建立在MAP意义下的贝叶斯扩展，均可以等价为一类正则化方法。
通过不同的正则化，可得到不同的针对特定偏爱的结果。例如，用
ℓ
1
范数取代式（3.2.1）中的平方范数，则得到
w
具有稀疏特性（sparsity）的解。所谓稀疏特性是指
w
中的一些分量更偏向于取0值。这里
w
的
ℓ
1
范数定义为其各分量的绝对值之和，即
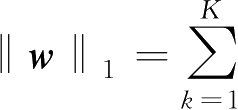|w
k
|，故具有稀疏解的回归目标函数为
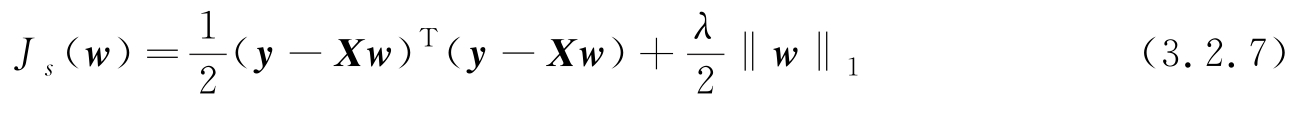
在一些特定情况下，稀疏约束可得到更有意义的结果，关于回归的稀疏学习可进一步参考文献[20]。
本节注释
在正则化过程中，对系数向量作为约束（惩罚）条件时，一般不将偏置
w
0
作为约束分量。在训练前，首先对输入向量
x
n
的每个分量进行归一化和零均值化，
w
0
由训练集标注的均值估计，即
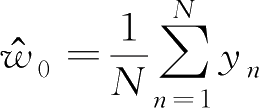，故
w
0
不参与式（3.2.1）的优化，对应式（3.2.3）的系数向量不包括偏置。本节对应式（3.1.12）中
X
的定义内第1列的全“1”列被删除。