




目前在机器学习中,对概率模型表示和相应的学习模型表示上,参数方法占主流地位。在概率模型估计中,首先假设一种数学形式表示的概率(密度)函数,例如高斯分布、混合高斯分布等,通过样本估计表征该概率函数的参数。但这种预先假设的模型是否成立,在实际中可能无法保证。非参数方法(non-parametric method)没有预先假设,可处理任意概率分布。
对于离散随机变量,其概率估计相对简单,在样本充分多时,只需采用概率的频率解释进行估计往往可得到满意的结果。故本节只讨论连续随机变量的概率密度函数估计问题。
设有样本集
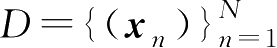 ,用于估计概率密度函数
p
(
x
)。对于一个给定的
x
,在其取值区间内构造一个以
x
为质心的充分小的区间
R
,设其体积为
V
,则向量
x
落在区间的概率
P
为
,用于估计概率密度函数
p
(
x
)。对于一个给定的
x
,在其取值区间内构造一个以
x
为质心的充分小的区间
R
,设其体积为
V
,则向量
x
落在区间的概率
P
为

设样本数 N 充分大,样本落在区间 R 内的数目为 K ,则概率 P 的另一种表示为 P ≈ K / N ,由式(2.7.1)得到

式(2.7.2)是非参数估计概率密度函数的基本公式,根据处理 V 和 K 的不同,分为两类方法,固定 V 的大小构成Parzen窗方法,固定 K 的大小构成 K 近邻方法。
为了使式(2.7.2)中 x 变化时,都可以数出区间内样本数目 K ,最基本的方法是定义表示超立方体的窗函数 φ ( x ),其定义如下:
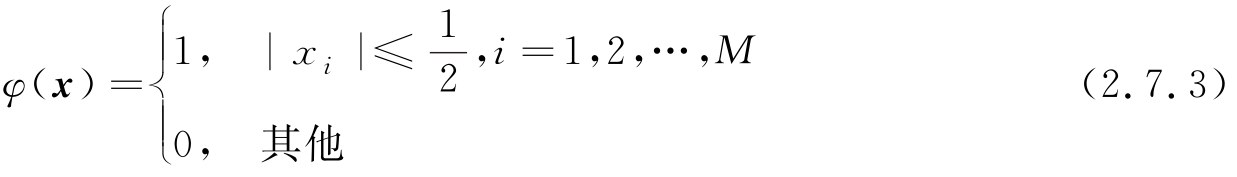
这里 M 是 x 的维数,对于大小固定的区间 R ,它的超立方体的边长为 h ,体积 V = h M ,由这些定义可见,在以 x 为中心的超立方体内的样本数可表示为

代入式(2.7.2)得Parzen窗概率密度函数估计为
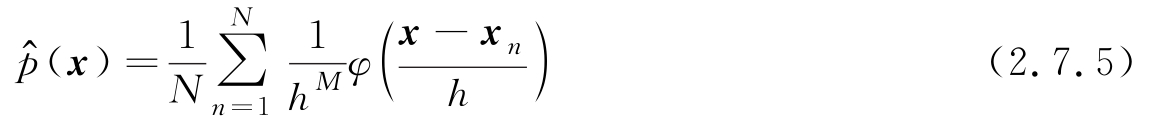
式(2.7.3)定义的超立方体窗估计的概率密度函数是分段台阶函数,不连续,可使用光滑窗函数代替超立方体窗,光滑窗函数需要满足如下两个条件:

高斯函数(此时表示窗函数而不是概率密度函数)是一个广泛使用的光滑窗,利用高斯窗函数,式(2.7.5)可重写为
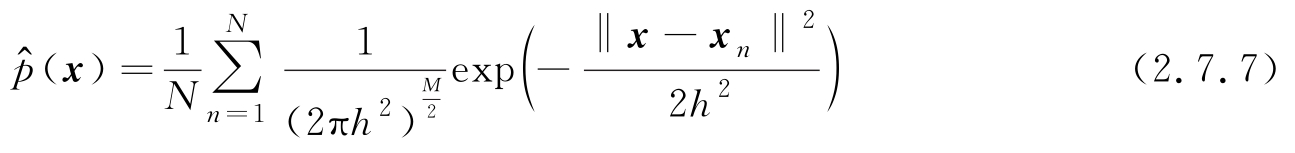
对于给定的样本集和不同的概率密度函数类型,表示体积大小的参数
h
的选择很重要,
h
太大则
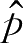 (
x
)的分辨力低,可能对真实概率密度函数的一些峰值产生模糊,
h
太小,则
(
x
)的分辨力低,可能对真实概率密度函数的一些峰值产生模糊,
h
太小,则
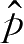 (
x
)起伏太大,因此需选择适中的
h
。已有结论指出,在一定条件下,当
N
→∞时,适当选择
h
,可使式(2.7.7)估计的概率密度函数收敛于真实函数,但在有限样本情况下,Parzen窗的逼近性质很难准确评价。
(
x
)起伏太大,因此需选择适中的
h
。已有结论指出,在一定条件下,当
N
→∞时,适当选择
h
,可使式(2.7.7)估计的概率密度函数收敛于真实函数,但在有限样本情况下,Parzen窗的逼近性质很难准确评价。
K
近邻方法可用于概率密度估计,其方法是选择并固定
K
,从零开始放大以
x
为中心的超球体,直到该球体中包含
K
个样本,计算超球体体积
V
代入式(2.7.2)计算
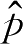 (
x
),然后移动
x
的值,重复计算新的概率密度函数值。由于
K
固定,在概率密度取值大的区域,样本密集,故球体体积小,估计的概率密度取值大,反之亦然。在实际中可适当选择
K
,例如选择
(
x
),然后移动
x
的值,重复计算新的概率密度函数值。由于
K
固定,在概率密度取值大的区域,样本密集,故球体体积小,估计的概率密度取值大,反之亦然。在实际中可适当选择
K
,例如选择
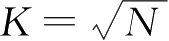 ,但
K
近邻方法往往不是对概率密度函数的一个理想估计,
K
近邻方法更多地用于构造一类简单的学习算法。
,但
K
近邻方法往往不是对概率密度函数的一个理想估计,
K
近邻方法更多地用于构造一类简单的学习算法。
第1章以 K 近邻分类器为例对分类器功能进行了说明,利用2.5节的决策理论可进一步解释 K 近邻分类器的原理。
设训练样本集
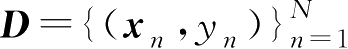 对应
C
1
,…,
C
J
共
J
种类型,总样本数为
N
,在训练集中各类型对应的样本数分别为
N
1
,…,
N
J
。对于一个给定的
x
,以其为中心的超球体内包括
K
个样本,体积为
V
。设近邻的
K
个样本中,标注为各类型的样本数分别为
K
1
,…,
K
J
,利用这些数据进行概率估计,显然
对应
C
1
,…,
C
J
共
J
种类型,总样本数为
N
,在训练集中各类型对应的样本数分别为
N
1
,…,
N
J
。对于一个给定的
x
,以其为中心的超球体内包括
K
个样本,体积为
V
。设近邻的
K
个样本中,标注为各类型的样本数分别为
K
1
,…,
K
J
,利用这些数据进行概率估计,显然
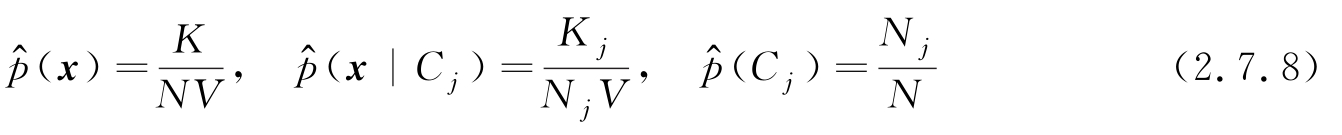
故后验概率为
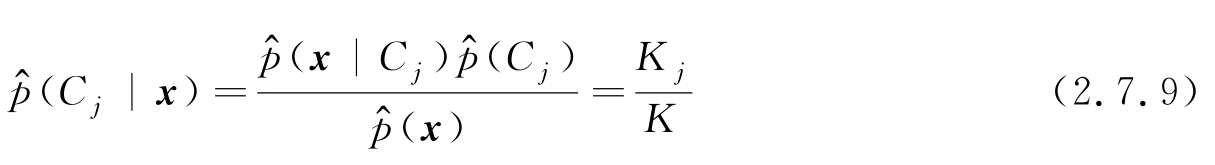
按照2.5节分类错误率最小的决策准则式(2.5.4),如果一个类型
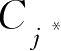 的后验概率最大,则输出为
的后验概率最大,则输出为
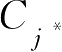 类。在
K
近邻算法中,由式(2.7.9)可见,
类。在
K
近邻算法中,由式(2.7.9)可见,
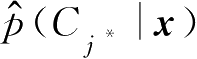 最大对应近邻样本数
最大对应近邻样本数
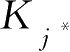 最多,则分类为
最多,则分类为
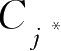 。可见
K
近邻分类器是一种建立在后验概率最大化基础上的分类器,只是后验概率的估计采用了
K
近邻概率估计。
。可见
K
近邻分类器是一种建立在后验概率最大化基础上的分类器,只是后验概率的估计采用了
K
近邻概率估计。
当 K =1时,分类器称为最近邻分类器,即将待分类的输入特征向量分类为距离最近的训练样本的类型,可以证明,用简单的最近邻分类器,当 N →∞时,分类误差不大于最优分类误差的2倍,若取较大的 K ,分类误差进一步降低。尽管简单,在一些应用中 K 近邻分类器可以获得可接受的分类效果,但 K 近邻分类器易受维数灾难的限制。
K
近邻方法同样可以用于回归估计,若样本集
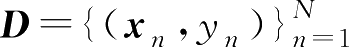 的标注是实数,对于一个给定的
x
,得到以其为中心的超球体,其内包括
K
个样本,记
x
的
K
个近邻样本集合为
D
K
(
x
),则
K
近邻回归输出为
的标注是实数,对于一个给定的
x
,得到以其为中心的超球体,其内包括
K
个样本,记
x
的
K
个近邻样本集合为
D
K
(
x
),则
K
近邻回归输出为

显然,这个输出近似等于 E ( y | x ),是利用 K 个近邻样本的标注值对 E ( y | x )的估计, E ( y | x )是式(2.5.14)给出的回归问题的最优决策值。