2.6　随机变量的熵特征

对于一个随机向量，其统计特性的最完整描述是联合概率密度函数（PDF）。在实际应用中，由联合PDF可导出各种统计特征用于刻画随机量的各种性质，其中熵特征用于表示随机量的不确定性，是一个很重要的特征。熵在电子信息领域已获得广泛应用，机器学习中的一些方法也采用了熵特征。

2.6.1　熵的定义和基本性质

首先针对随机变量 X 取值为离散的情况下讨论其熵特征。设 X 取值为离散集合{ x _i | i =1，2，…， N }，其中 X 取值 x _i 的概率为 p （ x _i ）= P { X = x _i }，则 X 的平均信息量或者熵定义为

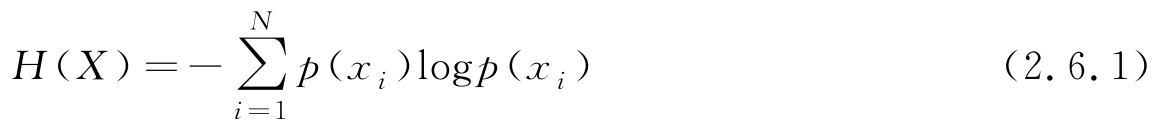
注意，log可取任意底，若取以2为底的对数，熵的单位为比特（bit），表示传输满足这一概率分布的一个变量平均所需要的最小二进制位数；若取自然对数，单位为奈特（nat），与比特量相差固定因子ln2。在机器学习中，在以熵特征作为评价准则表示模型时，熵取何种单位无关紧要，实际中可按照方便取对数的底。在以上定义中，若有 p （ x _i ）=0，规定 p （ x _i ）log p （ x _i ）=0。

一个离散随机变量熵的最小值为0，最小值发生在 p （ x _k ）=1， p （ x _i ）=0， i ≠ k 情况下，即 X 取 x _k 的概率为1，取其他值的概率为0，相当于是一个确定性的量。由于 p （ x _i ）满足约束条件 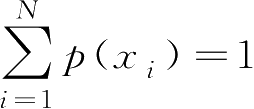，故通过优化下式得到熵的最大值

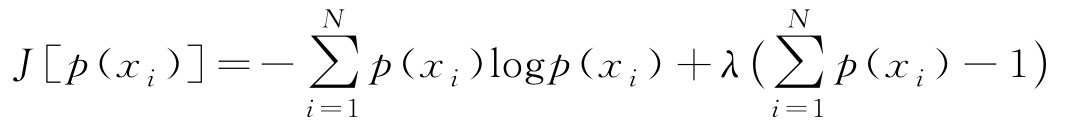
可求得当 p （ x _i ）=1/ N 时，熵的最大值是log N 。即等概率情况下，熵最大，也就是随机变量取值的不确定性最大。熵的大小确定了一个随机变量取值的不确定性，熵越大不确定性越高。

也可定义连续随机变量 X 的熵，设其PDF为 p （ x ）。为了利用式（2.6.1）导出连续情况的熵，将 X 的值域划分成 Δ 的小区间，变量取值位于区间[ iΔ ，（ i +1） Δ ]的概率可写为

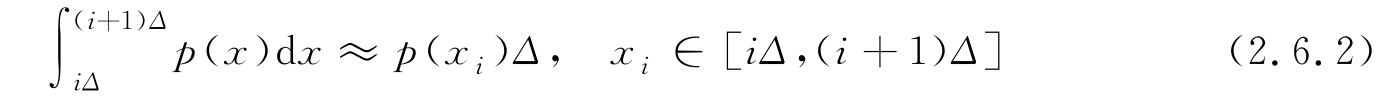
Δ 充分小时，连续随机变量的熵逼近为

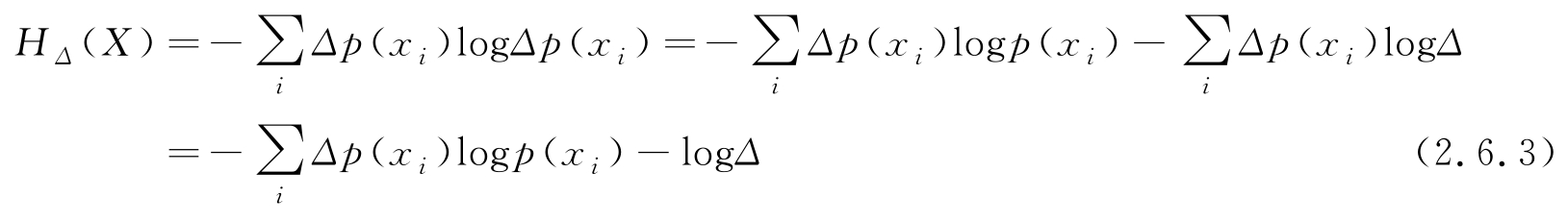
式（2.6.3）第2行利用了 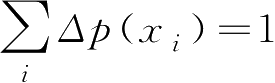，注意到，当 Δ →0时，-log Δ →∞，这容易理解：对于任意连续值的精确表示或传输需要无穷多比特位，但为了描述不同的连续变量之间熵的相对大小，只保留式（2.6.3）第2行的第一项并取极限，则进一步可写为

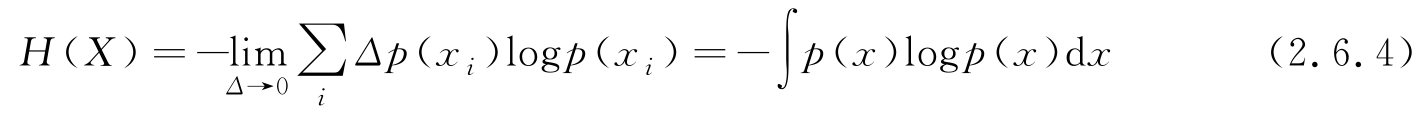
称式（2.6.4）定义的 H （ X ）为微分熵。注意，对于给定的PDF， X 的熵是确定的一个值，用类似于函数的符号 H （ X ）表示熵，是为了区分多个不同随机变量的熵，例如用 H （ X ）和 H （ Y ）区分 X 和 Y 的熵。

为了比较不同PDF的微分熵，需要附加两个限定条件，即在等均值 μ 和方差 σ ² 的条件下，比较哪种PDF函数具有最大熵？可求解如下约束最优问题：

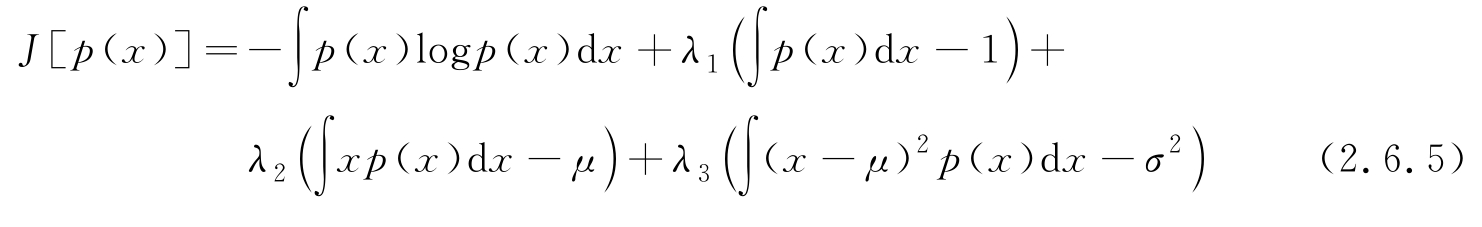
可证明，上式的解为

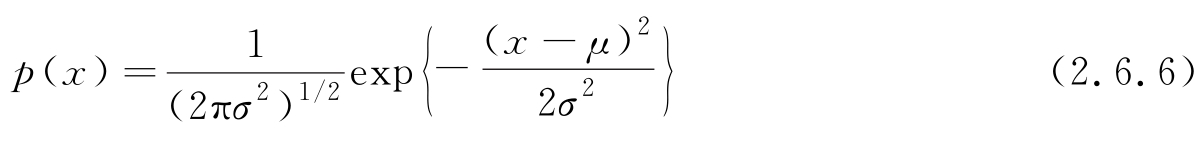
即在相同的均值 μ 和方差 σ ² 的条件下，高斯分布具有最大熵，且高斯过程的微分熵可表示为

对于一个随机向量 x =[ x ₀ ， x ₁ ， x ₂ ，…， x _{M -1} ] ^T ，其联合PDF可表示为 p （ x ），则式（2.6.4）的微分熵定义推广到多重积分（类似地，离散情况随机向量的熵推广到多重求和），形式化地表示为

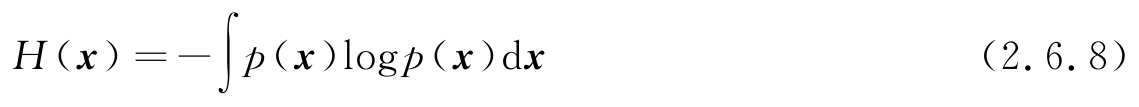
在同均值和协方差矩阵的所有PDF中，高斯分布

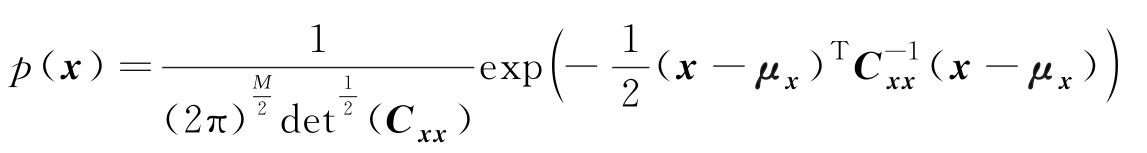
具有最大熵，且最大熵为

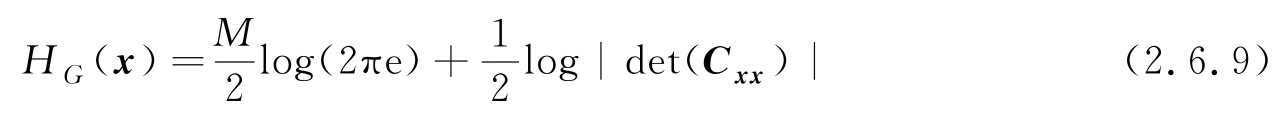
若存在两个随机向量 x 、 y ，其联合PDF为 p （ x ， y ），则联合熵和条件熵分别为

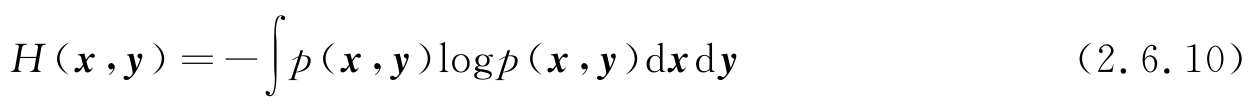
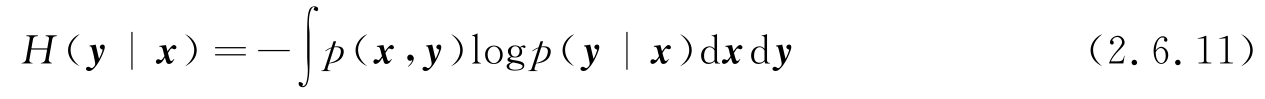
这里 H （ y | x ）是假设 x 已知的条件下 y 的条件熵，由积分公式易证明

H （ x ， y ）= H （ y | x ） +H （ x ）= H （ x | y ） +H （ y ）　（2.6.12）

若 x 、 y 相互独立，则

H （ x ， y ）= H （ x ） +H （ y ）

以上给出的是连续情况下的条件熵和联合熵，对离散情况用多重求和替代积分，结果是一致的。以下给出离散情况下条件熵的更有直观意义的表示

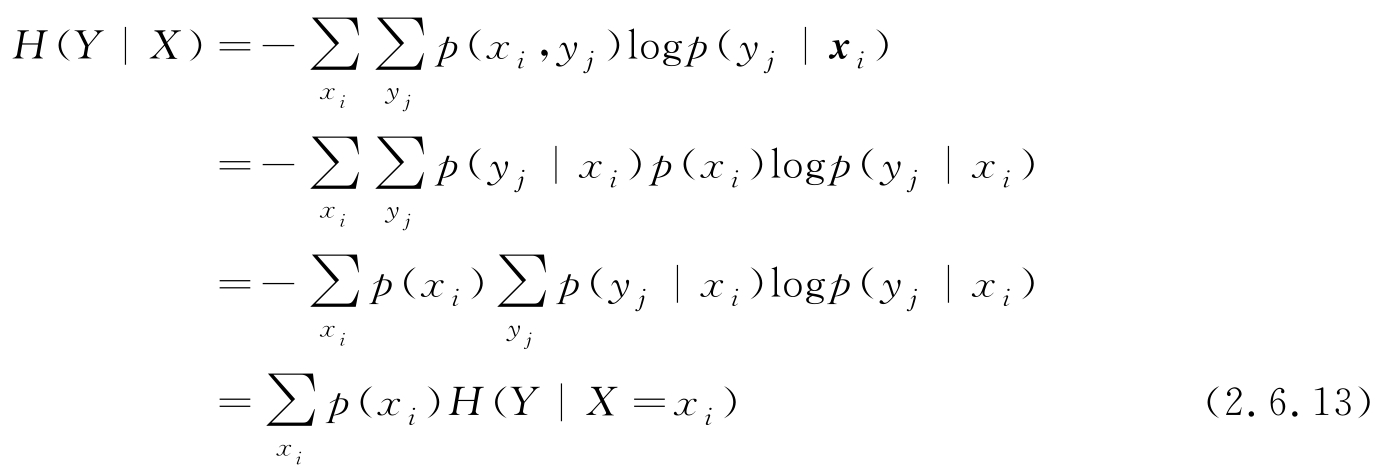
其中， H （ Y | X = x _i ）表示 X = x _i 的特定值时 Y 的条件熵。

2.6.2　KL散度

有两个PDF p （ x ）和 q （ x ），一种度量两个PDF之间不同的量KL散度（Kullback-Leibler divergence）定义为

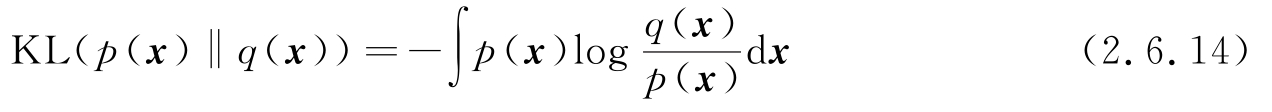
KL散度也称为相对熵。可以证明，对于任意两个PDF，其KL散度大于或等于0，即

KL（ p （ x ）‖ q （ x ））≥0　（2.6.15）

利用Jensen不等式可以证明式（2.6.15）。对于一个凸函数 f （ y ）和随机向量 y ，Jensen不等式写为

E [ f （ y ）]≥ f （ E [ y ]）　（2.6.16）

这里 E [·]表示取期望。由于-log y 是凸函数，令 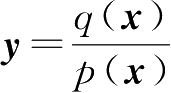，则对 p （ x ）取期望得

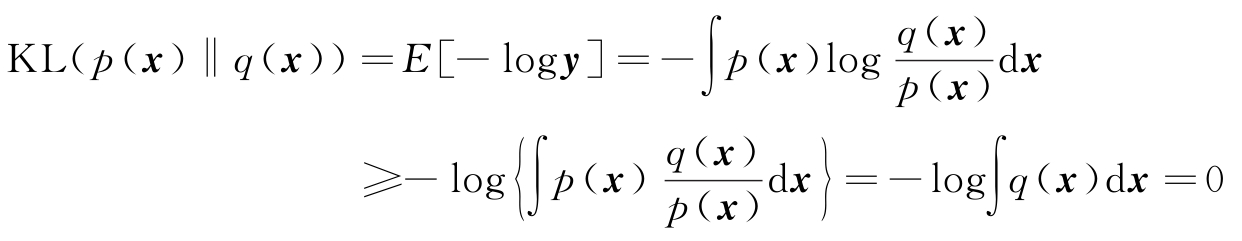
故得证KL（ p （ x ）‖ q （ x ））≥0，且只有在 p （ x ）= q （ x ）时，KL（ p （ x ）‖ q （ x ））=0。

从式（2.6.14）中KL散度的定义可知，可将其视为函数 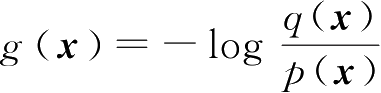在概率 p （ x ）意义下的期望值，即 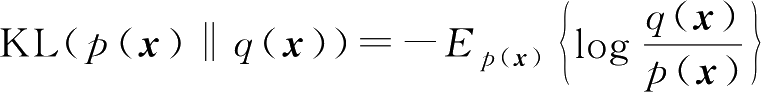。在给出I.I.D样本集 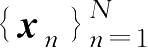的情况下，由2.1.5节给出的随机特征的蒙特卡洛逼近式（2.1.37），KL散度的样本逼近计算为

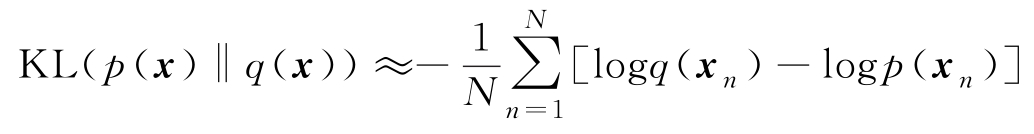
如果面对的问题是用样本集学习一个参数模型用于逼近 p （ x ），则将描述参数模型的概率函数 q （ x ）= （ x | w ）代入上式，有

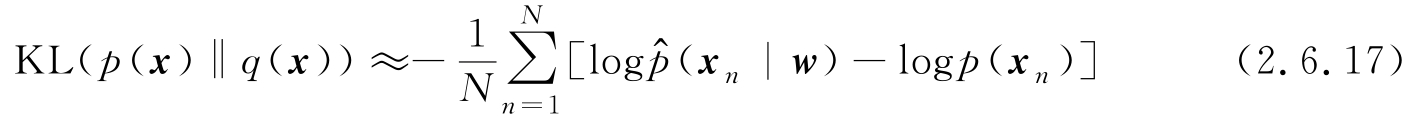
若求参数向量 w 使得 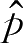（ x | w ）尽可能逼近 p （ x ），则相当于求 w 使KL（ p （ x ）‖ q （ x ））最小（理想逼近时为0）。由于log p （ x _n ）是与 w 无关的常量，故求KL散度最小相当于只需要

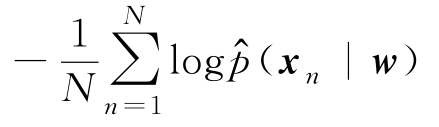
最小，这与最大对数似然函数（式（2.3.7））是一致的。即在利用I.I.D样本集求解机器学习的参数模型问题上，KL散度最小准则和最大似然准则近似等价。 DVSdrGvhrpfJIzO8F35PaUCqp9wG2vCMa0xmkqxErwVWCJ9cwlWKGkauh/0sZEr5