




李剑辉,郑玲,李以农,乔旭强,张紫薇
重庆大学机械与运载工程学院
【摘要】 为改善自适应巡航 ( adaptive cruise control , ACC ) 系统的跟踪性能和舒适性,本文提出了一种考虑驾驶人特性和前车加速度扰动的ACC控制算法。首先,基于驾驶数据,建立驾驶人跟车模型 ; 其次,考虑前车加速度的扰动,提出基于高斯过程 ( gaussian process,GP ) 的前车加速度在线预测方法 ; 最后设计了基于模型预测控制 ( model predictive control , MPC ) 的ACC算法,以实现基于安全、舒适、节能等多目标,并考虑驾驶人驾驶偏好的拟人化自适应巡航 ( ACC ) 控制。仿真结果表明,与传统的LQR算法相比,本文提出的拟人化ACC算法能够在车辆跟随过程中,充分体现了驾驶人的驾驶习惯,改善了ACC系统的舒适性和宜人性。
【关键词】 自适应巡航控制,驾驶人特性,GP算法,模型预测控制
Research on Human-like ACC Algorithm Based on Gaussian Process
Li Jianhui, Zheng Ling, Li Yinong, Qiao Xuqiang, Zhang Ziwei
College of Mechanical and Vehicle Engineering , Chong Qing University
Abstract: An ACC algorithm that fully considers the characteristics of the driver and disturbance of the preceding vehicle is pro-posed in order to improve tracking performance and comfort of the Adaptive Cruise Control (ACC) system in this paper. Firstly, the driver car-following model is established based on the driving data; Afterwards, aiming at disturbance of preceding vehicle, an online prediction method of the acceleration of the leading vehicle based on Gaussian Process (GP) is proposed. Finally, an MPC-based ACC algorithm is designed to realize the human-like adaptive cruise control (ACC) based on safety, comfort, energy-saving and other ob-jectives, and considering the driver's driving preferences. The simulations show that, compared with the traditional LQR algorithm, the human-like ACC algorithm in this paper can demonstrate the driving habits for drivers, which will help to improve the agreeableness and the comfort of the ACC system.
Key words: ACC, driver characteristics, gaussian process, model predictive control
作为一种先进的驾驶辅助系统(advanced driver assistant systems,ADAS),自适应巡航(ACC)系统能够根据前方的行驶环境,自动调整车速,跟随前车行驶,减轻驾驶人的精神负担并减少交通事故 [1] 。
在过去的几十年里,国内外学者做了大量关于ACC的研究,许多算法在ACC上得到了应用,例如PID控制、模糊控制、机器学习 [2] 、最优控制 [3] 、模型预测控制 [4] 等。近年来,由于MPC采用预测模型、滚动在线优化以及反馈校正机制,具备同时兼顾系统I/O约束与过程状态约束,动态协调巡航过程中的多个控制目标等优势,使控制效果与鲁棒性皆能明显改善而被广泛应用于ACC的设计中 [5] 。文献[6-8]利用MPC理论降低了电驱动车辆的能耗;文献[9-13]通过MPC理论将ACC的多目标决策问题转化成带约束的在线QP二次规划问题,实现了基于安全、舒适的ACC系统多目标协同控制。
然而,基于规则的ACC策略并不符合驾驶人的驾驶习惯,从而导致ACC使用率低和接受度差的问题,并且由于忽略了前车的加速度扰动,严重影响了其跟踪性能。为此,很多学者开始将驾驶人特性和MPC相结合,并应用于ACC的设计中,文献[1]分析了驾驶人的驾驶习惯,在MPC框架下提出了一种双模式ACC算法;文献[14]基于驾驶姿态识别和恒定的时间间隔,建立了基于MPC理论的个性化ACC系统。在上述研究中,通常使用安全距离模型和相对速度作为控制目标,但这并不能充分反映驾驶人的跟随特征。
为了得到最优解,MPC预测模型必须准确可靠。而ACC的MPC模型不仅与自车有关,而且与前车相关,尤其是加速度。关于前车的加速度扰动问题,文献[15]采用闭环控制策略,补偿前车加速度扰动的影响,文献[16]利用最小二乘的方法预测前车加速度的变化规律,并应用于跟车模型的模型预测框架中,前者采用大量的离线计算,而后者假设加速度近似沿着直线变化,都无法准确反映前车加速度的变化规律。因此导致所得到的最优解会偏大或偏小。
本文利用驾驶模拟器采集驾驶人跟车数据,并利用这些数据分析驾驶人的跟车特性和误差敏感度,建立驾驶人跟车模型;基于GP算法对前车加速度进行在线预测,进而应用到跟车模型的模型预测框架中作为加速度扰动预测值,实现了MPC预测模型的准确构建;最后,基于驾驶人模型和前车加速度预测模型,提出考虑舒适性、安全性以及经济性等多性能目标的拟人化ACC控制系统。
基于仿真驾驶模拟器、prescan、carsim软件等搭建驾驶数据采集平台,如图1所示。建立城际高速跟车场景,采集驾驶人操控信息、主车行驶状态信息、他车状态信息。招募具有中国机动车驾驶执照的驾驶人20名,均持照1年以上,且身体健康。在实验开始之前,先对实验平台进行一段时间的试驾驶,以熟悉车辆和实验步骤。为了消除随机性误差,实验进行三次采样。

图1 驾驶人数据采集装置
跟车过程中,驾驶人的期望车距采用期望距离模型来描述。相关研究表明,驾驶人的期望车距与自车车速近似于二次函数形式 [17] ,并且该模型结构形式简单,被广泛应用于控制领域。因此,建立二次型期望车距模型如下:

式中, v f 为自车加速度; d des 为期望距离; a , b , c 为模型参数,可以基于采集的驾驶人跟车数据,用最小二乘法求解。其拟合结果如图2所示。为了便于观察,需要做出数据点的概率密度图,红色曲线为拟合曲线。
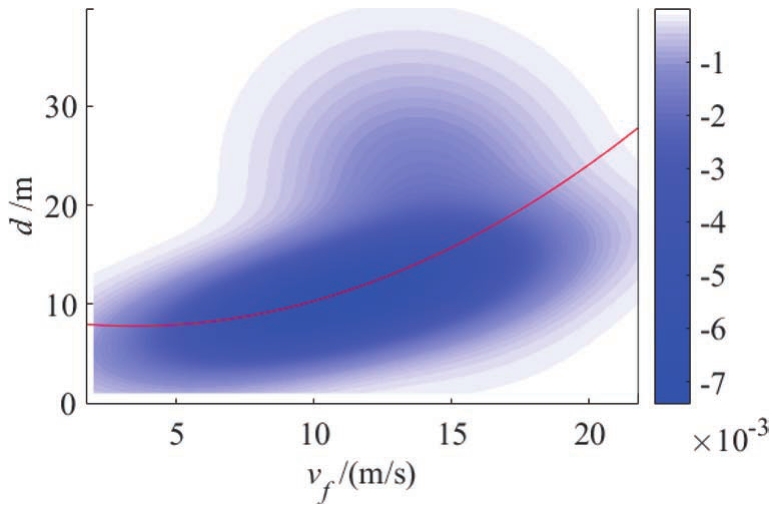
图2 驾驶人期望距离模型
在跟车过程中,车辆行驶的加速度主要受相对速度和相对距离的影响。当自车速度小于前车速度,或者实际相对距离大于驾驶人的期望距离时,驾驶人会进行加速。驾驶人的线性跟驰模型可描述为

式中,Δ v 为相对速度;Δ d 为相对距离误差,Δ d = d des -d ; a fr 为自车期望加速度; k v , k d 为控制增益。
对于同一驾驶人,控制增益会随车距和车速的不同发生变化 [18] ,并且当控制增益正比于车速时,跟踪效果更好,因此,引入速度灵敏度( VS )和距离灵敏度( DS )来对线性跟驰模型进行改进:
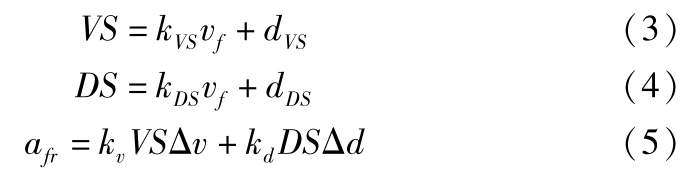
式中, k VS , d VS , k DS , d DS 为常量参数。为了求取这些参数,首先对 VS 和 DS 进行量化,这里用相关性系数来量化 VS 和 DS 。
对 VS 进行量化时,为排除相对距离的影响,让Δ d 约等于0。因此,对数据进行筛选:

将筛选后的数据按照速度从小到大分为14组,每组数据中心速度处 VS 的量化值定义为:
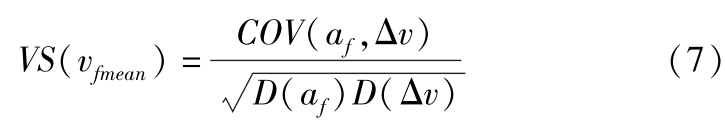
式中, a f 为自车加速度; v f 为自车速度; COV ( a f ,Δ v )为第 m 组数据 a f 与Δ v 的协方差; D ( a f )为第 m 组数据 a f 的方差; D (Δ v )为第 m 组数据Δ v 的方差。
对 DS 进行量化时,为排除速度的影响,让Δ v 约等于0。因此,对数据进行筛选:

将筛选后的数据按照速度从大到小分为14组,每组数据中心速度处 DS 的量化值定义为:
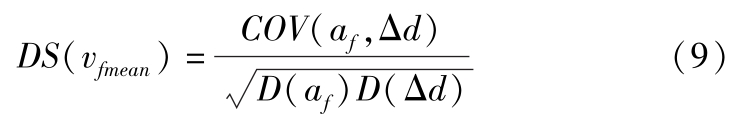
式中, COV ( a f ,Δ d )为第 m 组数据 a f 与Δ d 的协方差; D ( a f )为第 m 组数据 a f 的方差; D (Δ d )为第 m 组数据Δ d 的方差。
采用最小二乘法对数据进行参数拟合,其结果如图3所示。当速度增大时,其 VS 和 DS 都增大,这说明速度越大,驾驶人对速度和相对距离的变化越不敏感。改进后的跟驰模型结果如图4所示,可以看出该模型对驾驶人跟车特性具有非常好的描述能力。
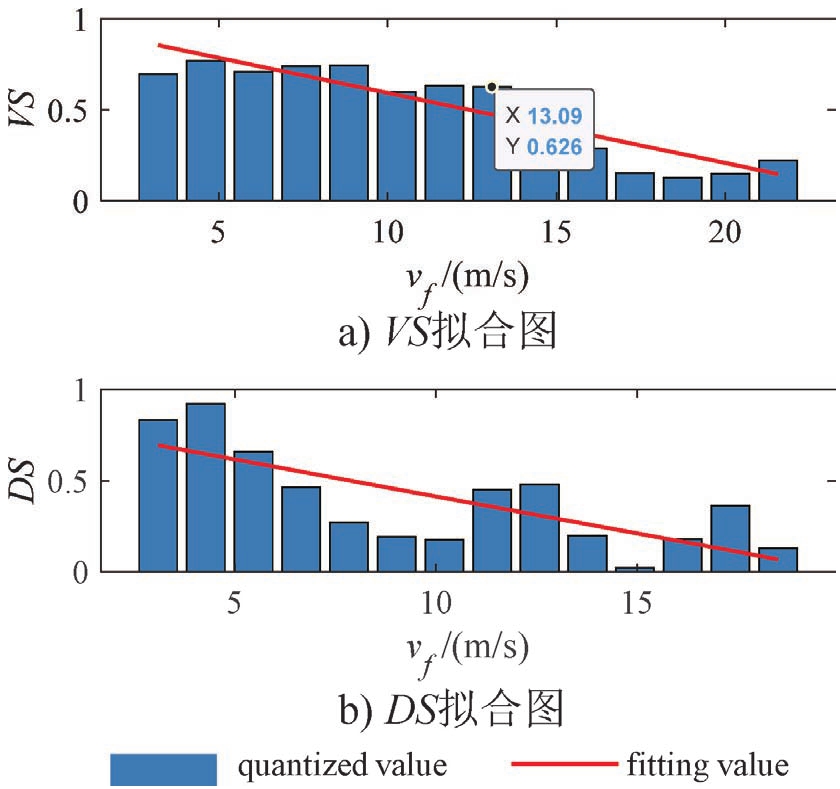
图3 驾驶人灵敏度分析
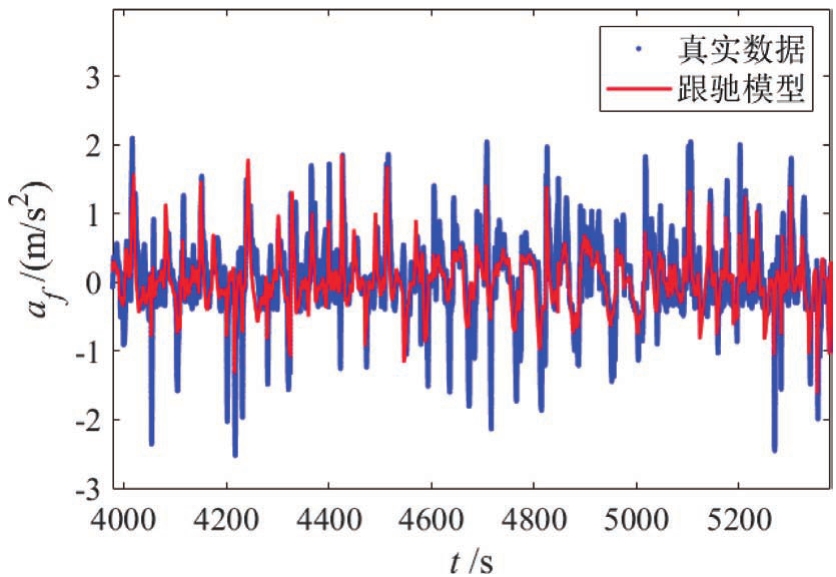
图4 改进后的跟驰模型
在跟车过程中,当车辆状态不同时,相同跟随误差所造成的驾驶人感受是不同的,如相对速度为5m/s,车速较低时驾驶人很难接受,但是车速较高时,驾驶人则更容易接受。
驾驶人敏感度是反映驾驶人对不同状态下跟踪误差导致的影响驾驶人感受的一种度量,用以说明不同行驶状态下驾驶人对某项跟踪误差的关心程度。纵向控制包含速度误差敏感度( SVE )、相对距离误差敏感度( SDE )、加速度误差敏感度( SAE ),其定义如下 [19] :

式中, k SVE , d SVE , k SDE , d SDE , k SAE , d SAE 是常量参数。为了利用求取这些参数,需要利用驾驶数据量化敏感度误差。
当Δ d 和 a f 接近于零,车辆状态处于稳定,且没有距离误差,而此时Δ v 的分布越离散,说明驾驶人对于Δ v 的敏感度越低,反之则越高,Δ v 的标准差可以反映其离散程度,因此用Δ v 的标准差的来量化 SVE ,当 SVE 越大时,说明驾驶人越不敏感。
首先,筛选出当Δ d 和 a f ,接近于零的数据,筛选标准为

再将筛选后的数据按照速度从大到小分为14组,而每组数据中心速度处 SVE 的量化值定义为
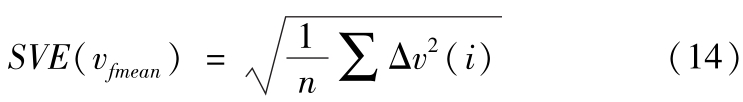
同理,量化 SDE 时,数据筛选标准为

再将筛选后的数据按照速度从大到小分为14组,每组数据中心速度处 SDE 的量化值定义为
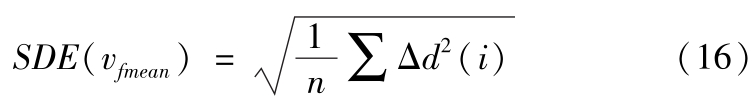
量化 SAE 时,数据筛选标准为

再将筛选后的数据按照速度从大到小分为14组,每组数据中心速度处 SAE 的量化值定义为
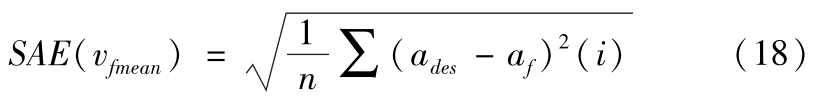
采用最小二乘法对其进行拟合,结果如图5所示。可以看出,随着速度增大, SVE 和 SDE 也增大,这说明高速时驾驶人对车辆状态的敏感度降低。但是 SAE 随着速度增大而略微减小,这是因为高速时,驾驶人更加注重对车辆的掌控,虽然对车辆状态的误差敏感度下降,但是对操作信息的敏感度增大。
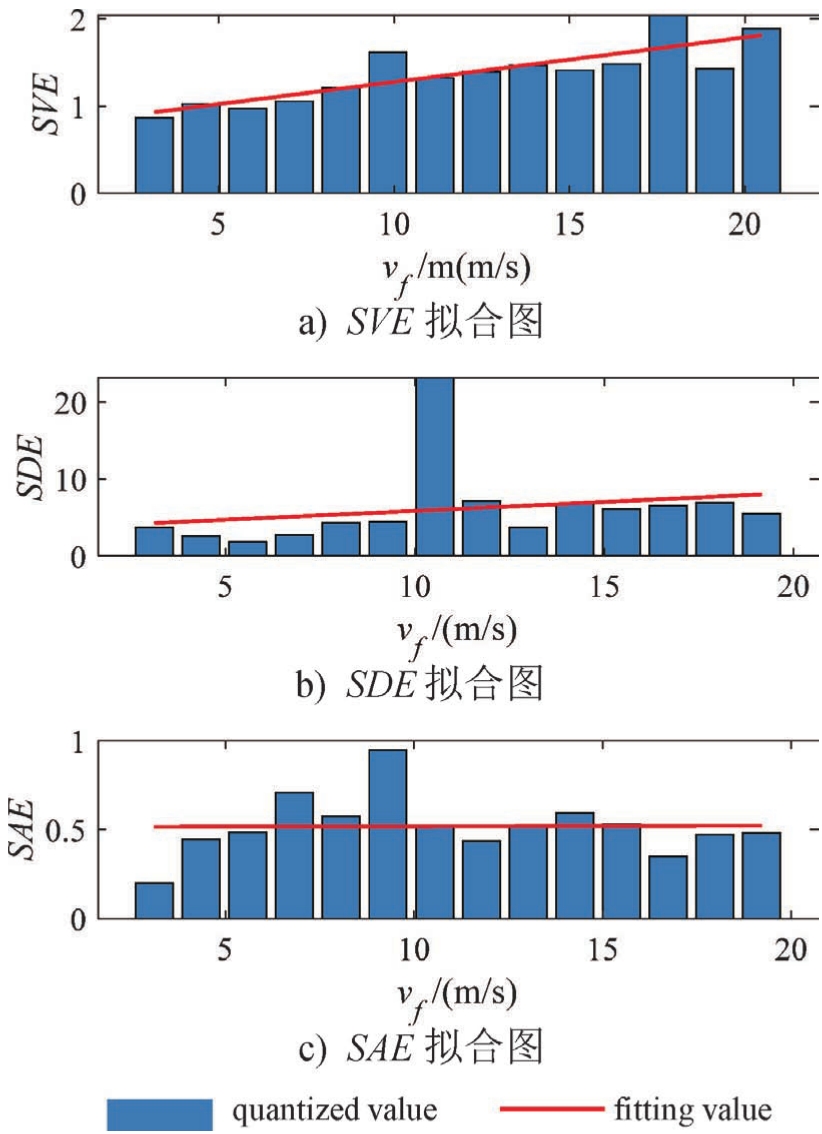
图5 一般型驾驶人敏感度模型
通过敏感度分析,可以建立反映驾驶人偏好的权重调节机制应用于MPC中,来真实反应驾驶人的驾驶特性,提高乘坐舒适性和宜人性。
基于MPC的ACC控制不仅与自车状态有关,而且还与前车状态相关,尤其是加速度。因此本文采用GP来对前车加速度进行在线预测。
首先选择时间作为GP算法的特征
x
,前车加速度作为标记
f
,假设当前时刻为
x
n
,以
x
1
到
x
n
的观测量作为训练集,则输入空间为
x
={
x
1
,
x
2
,…,
x
n
},输出空间
f
={
f
1
,
f
2
,…,
f
n
},预测时域内输入空间
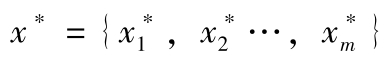 ,输出空间
,输出空间
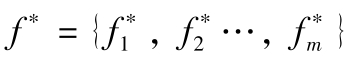 。GP算法将每个输出作为一个高斯分布,则观测时域与预测时域内输出的联合概率分布为
。GP算法将每个输出作为一个高斯分布,则观测时域与预测时域内输出的联合概率分布为
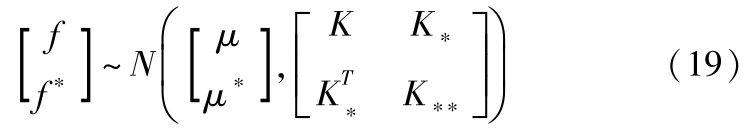
式中, K 为 f 的协方差矩阵; K * 为 f 与 f * 的协方差矩阵; K ** 为 f * 的协方差矩阵。 K 由径向基核函数构成,其定义如下:
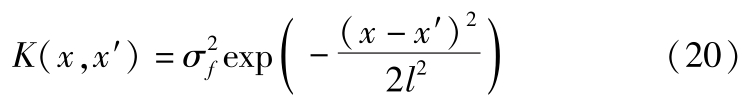
式中, θ =[ σ f , l ]为超参数,可通过极大似然估计得到:
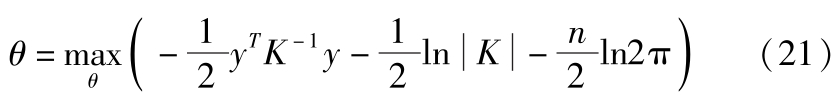
由多元高斯分布的条件概率公式,可以推出在观测到 f 的条件下预测时域内 f * 的分布为
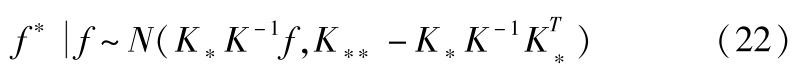
利用过去10s内的信息预测未来2s内的前车加速度,其结果如图6所示。可以看出预测结果和真实值的变化基本一致。
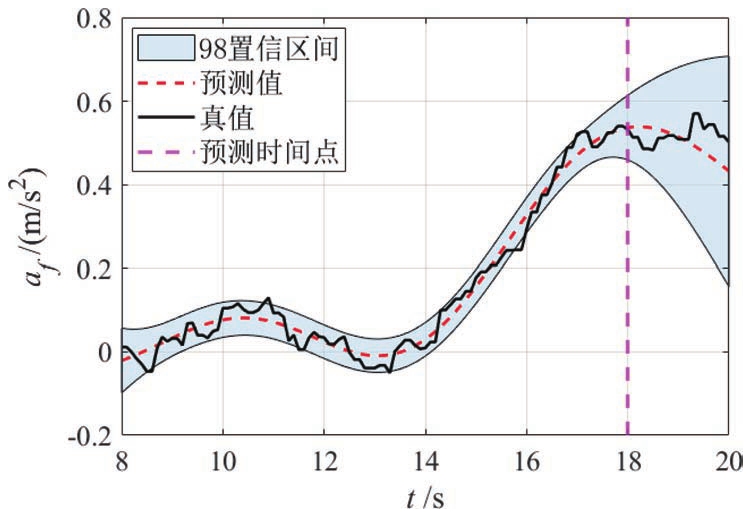
图6 前车加速度预测
根据汽车系统结构,采用频率响应法辨识其输入输出特性,其传递函数为 [12]

式中, a des 为汽车的期望加速度; K g 为系统增益; T g 为系统延迟。
车间运动表达式为

式中, s p 为前车位置; s f 为自车位置; v p 为前车速度。综合式(1)、式(23)和式(24)可得:
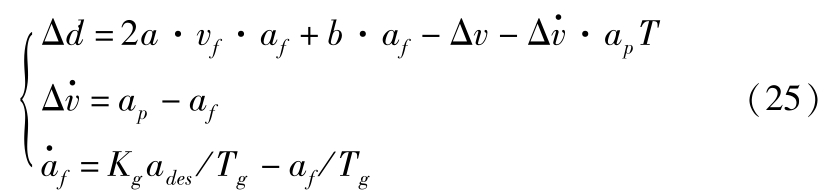
式中, a p 为前车加速度; T 为采样步长。取系统状态变量 x =[Δ d ,Δ v , a f ] T ,控制量 u = a des ,扰动 η = a p ,建立广义纵向动力学模型:

式中,各系数矩阵满足
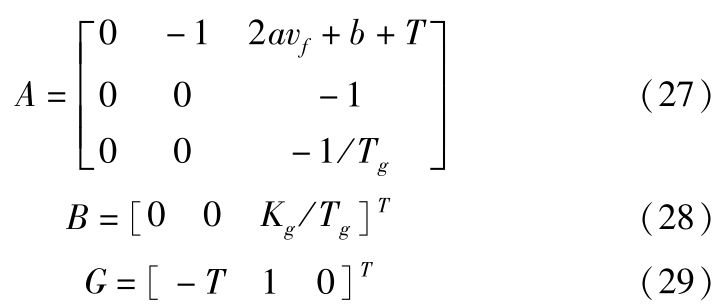
将式(26)进行线性化和离散化:
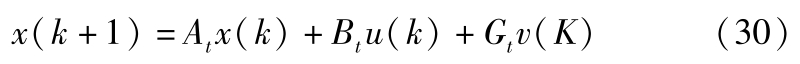
式中, A t = I + AT , B t = BT , G t = GT 。
取系统输出为 y =[Δ d ,Δ v , a f ] T ,则系统输出方程为

式中,输出系数矩阵 C = I 3x3 。
在ACC设计过程中,必须在确保安全性的前提下,综合考虑驾驶人的舒适性和燃油经济性。因此,采用二次型性能指标以及线性不等式约束形式,将纵向期望加速度的决策问题转化成带约束的在线QP二次规划问题 [5] 。
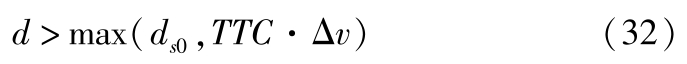
式中, TTC 为碰撞时间; d 为实际车距; d s0 为极限安全车距。
为保证驾驶人良好的驾驶体验,车辆行驶过程中的速度、相对距离、加速度应与驾驶人的期望值接近。因此,其代价函数为
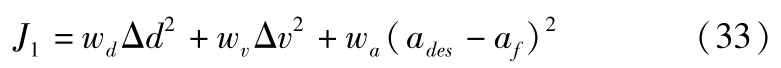
式中,期望加速度 a des 由式(5)得到。
当车辆状态发生变化时,驾驶人对相应误差的敏感度会随之改变。因此,可以通过驾驶人误差敏感度改变相应的权重系数来真实反映驾驶人的驾驶特性:

线性不等式约束条件为
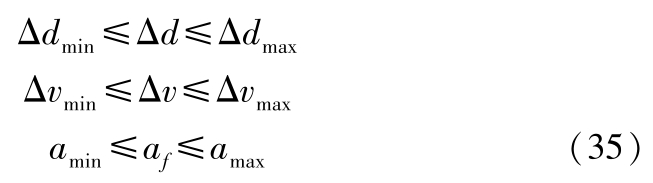
式中,Δ d min ,Δ v min , a min ,Δ d max ,Δ v max , a max 分别为系统输出的上下限。
在行驶过程中,燃油经济性主要和车速、加速度、加速度变化率有关。一般来说,车速主要受行驶环境影响,减少车辆加减速的次数,可以提高燃油经济性,其代价函数为

式中,Δ u 为 u 在单位步长内的变化量。
受车辆动力性约束,对车辆状态进行限制:
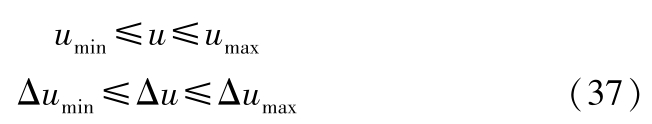
假定预测时域为 N p ,建立预测时域内的系统输出量
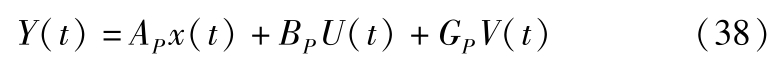
其中,
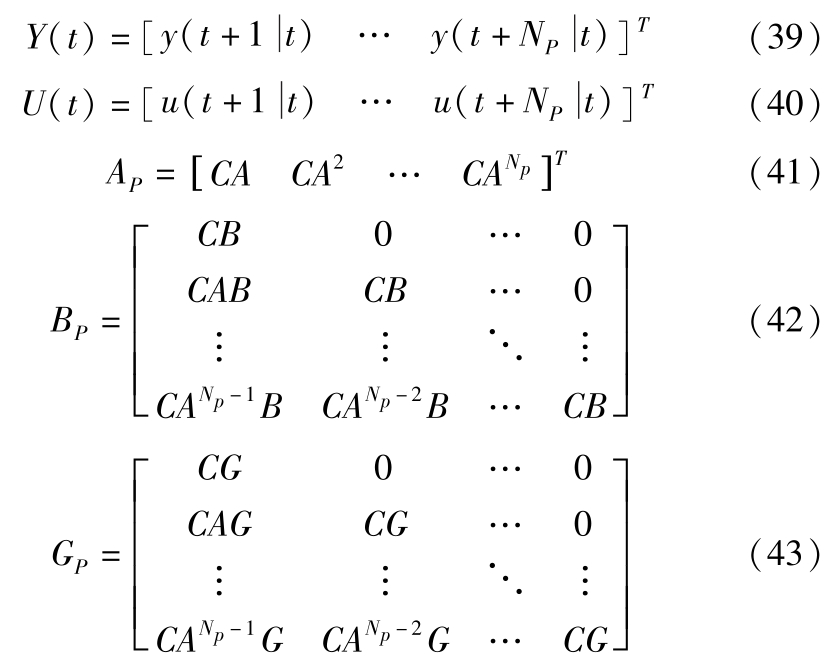
结合式(30)和式(33),建立优化目标,为保证优化目标存在可行解,需在优化目标中加入松弛因子并化简:
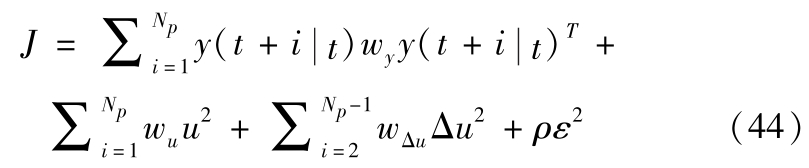
其中,各权重矩阵满足:
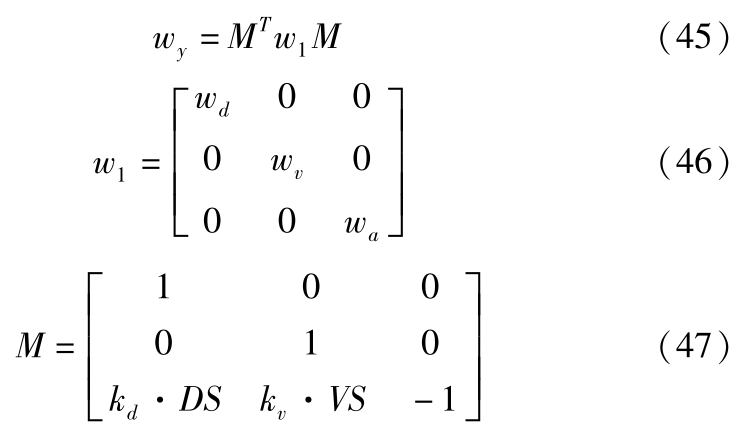
结合式(35)得:
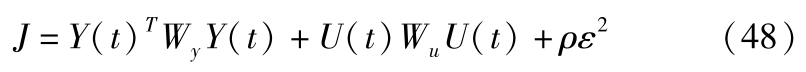
式中,
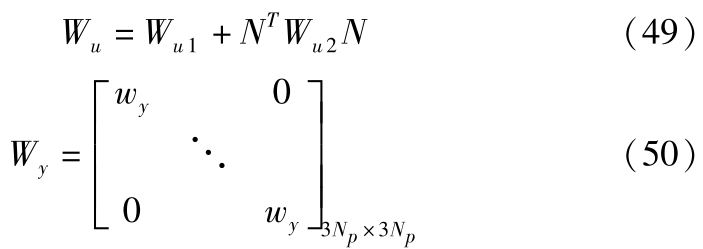

对约束条件松弛化,将上述问题转化二次规划问题:
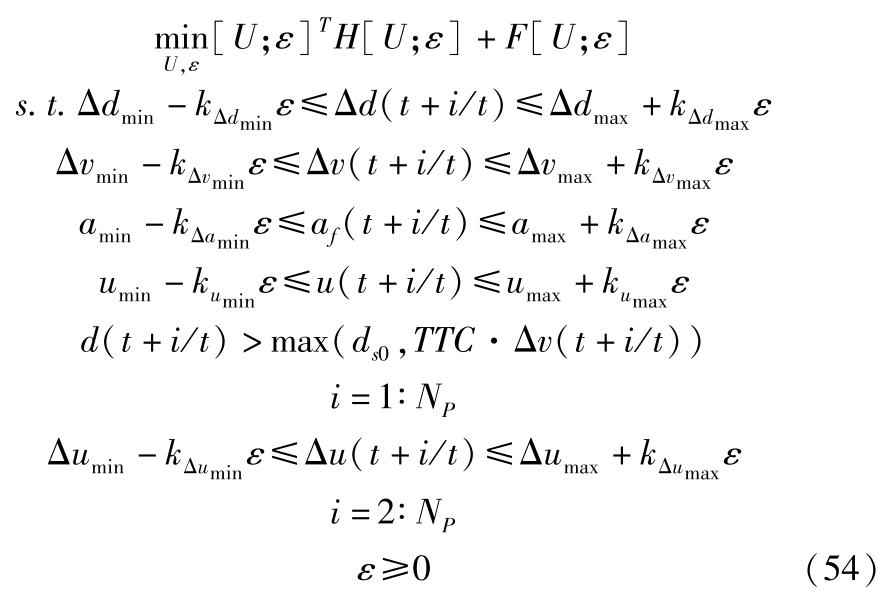
式中, k Δ d min , k Δ d max , k Δ v min , k Δ v max , k a min , k a max , k u min , k u max , k Δ u min , k Δ u max , k Δ d min , k Δ d max , k Δ v min , k Δ v max , k a min , k a max , k u min , k u max , k Δ u min , k Δ u max 为约束条件的松弛系数。因为式(29)为安全约束,不能进行松弛化。二次规划系数矩阵满足
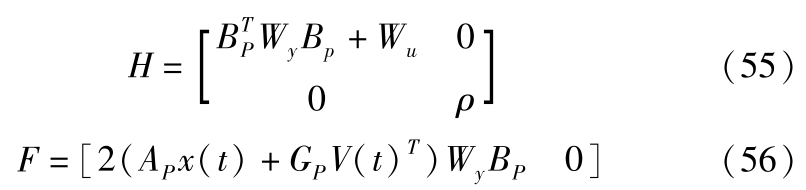
利用MATLAB/Simulink搭建ACC控制模型、逆纵向动力学模型、车辆动力学模型,进行控制算法的仿真测试,并与LQR算法进行对比。仿真工况包括急加速工况和急减速工况。
在LQR算法中,控制目标为车间距离误差,控制律为
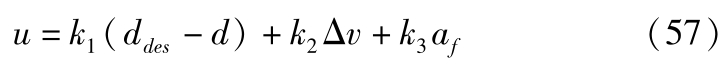
式中, k 1 , k 2 , k 3 为状态反馈系数, k 1 =0.3842, k 2 =1.1363, k 3 =-0.8249。
自车与前车初始速度皆为10m/s,前车于15s左右开始加速至18m/s,仿真结果如图7~图9所示。当前车加速时,LQR-ACC与MPC-ACC都进行加速,但从图8和图9可以看出,MPC-ACC先于LQR-ACC进行加速,这是因为MPC-ACC采用GP算法对前车加速度进行了预测。从图7和图8可以看出MPC-ACC的收敛速度明显优于LQR-ACC。
自车与前车初始速度皆为18m/s,前车于15s左右开始减速至4m/s,仿真结果如图10~图12所示。从图11和图12可以看出,MPC-ACC的加速度绝对值要略小于LQR-ACC,但MPC-ACC的减速效果要优于LQR-ACC。图10表明LQR-ACC出现了车距为3.5m的危险工况,而MPC-ACC减速平稳。
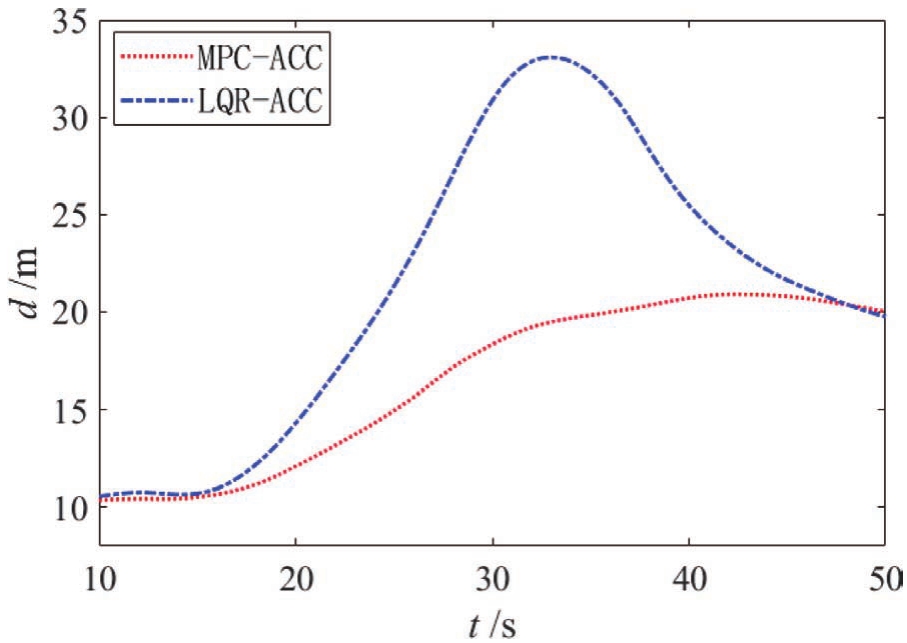
图7 前车急加速工况车距曲线
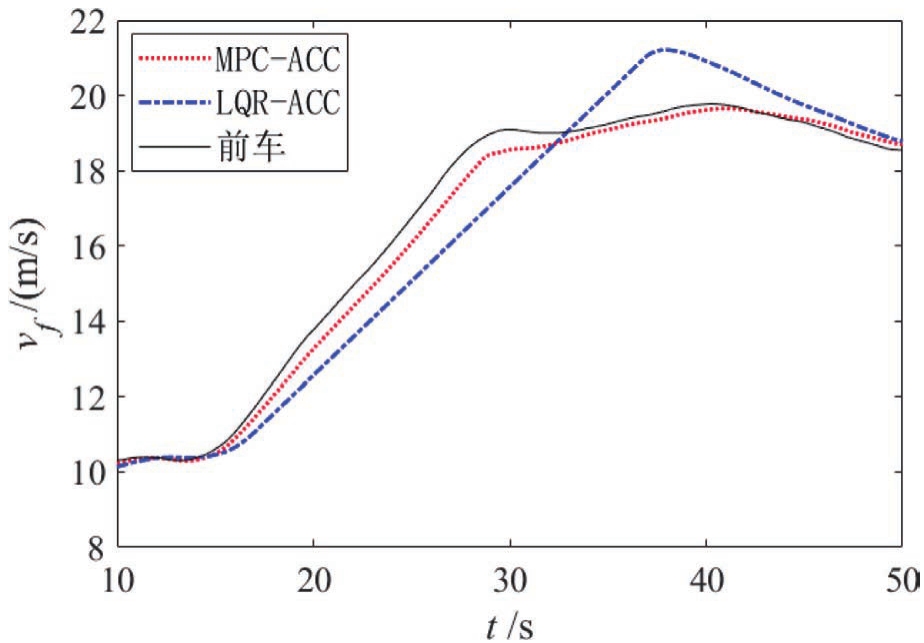
图8 前车急加速工况速度曲线
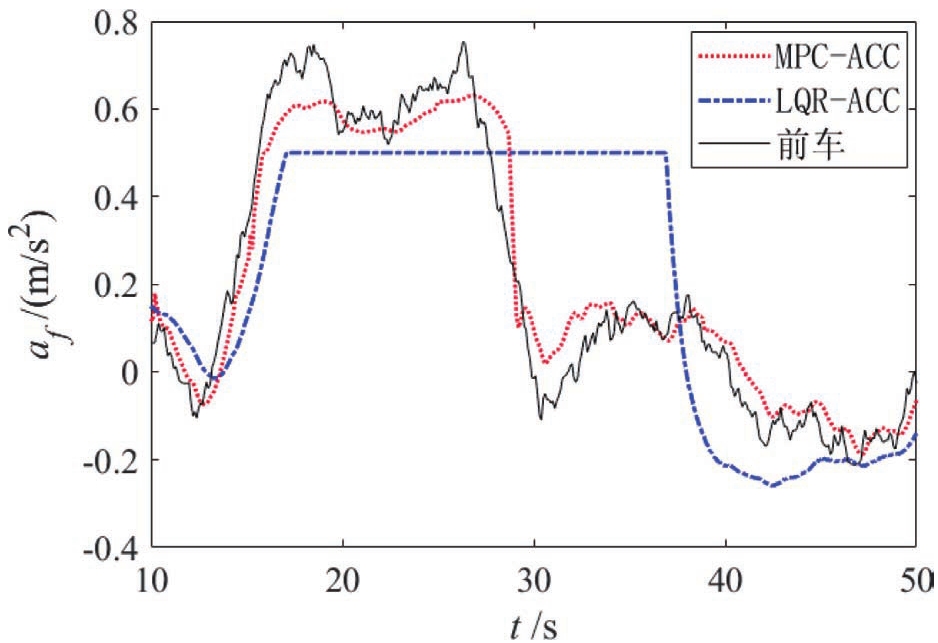
图9 前车急加速工况自车加速度曲线
从以上结果可以看出,考虑了驾驶人特性和前车加速度扰动的多目标ACC控制系统,可以体现驾驶人的驾驶偏好,实现拟人化的自适应巡航控制功能。
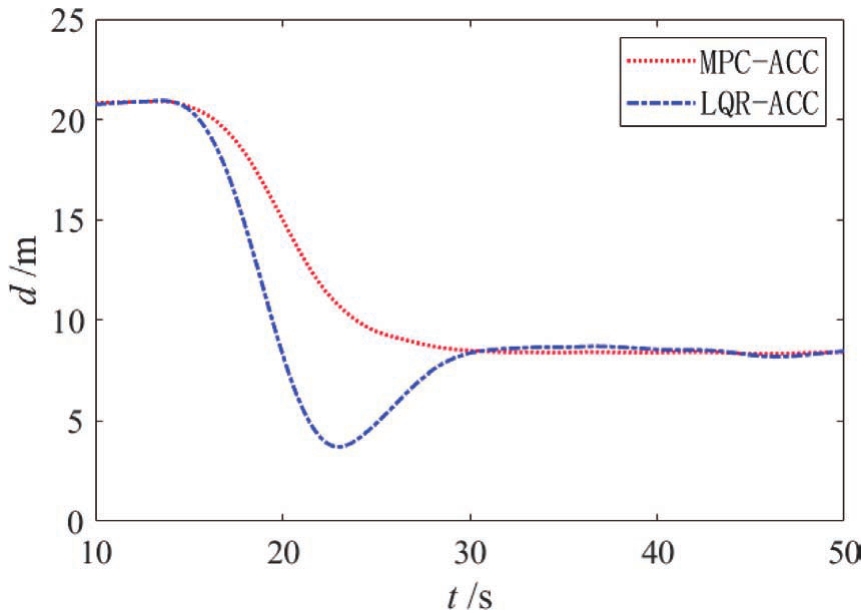
图10 前车急减速工况车距曲线
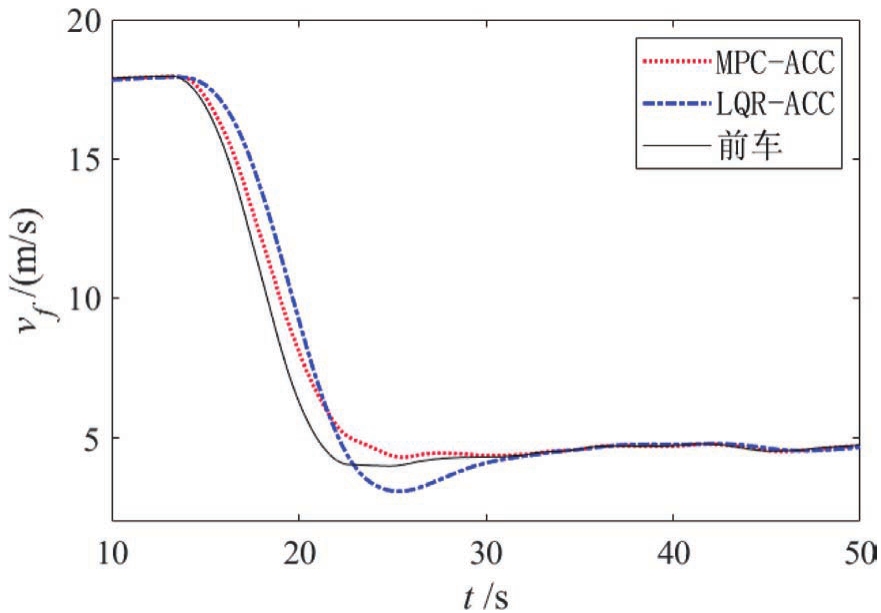
图11 前车急减速工况车速曲线
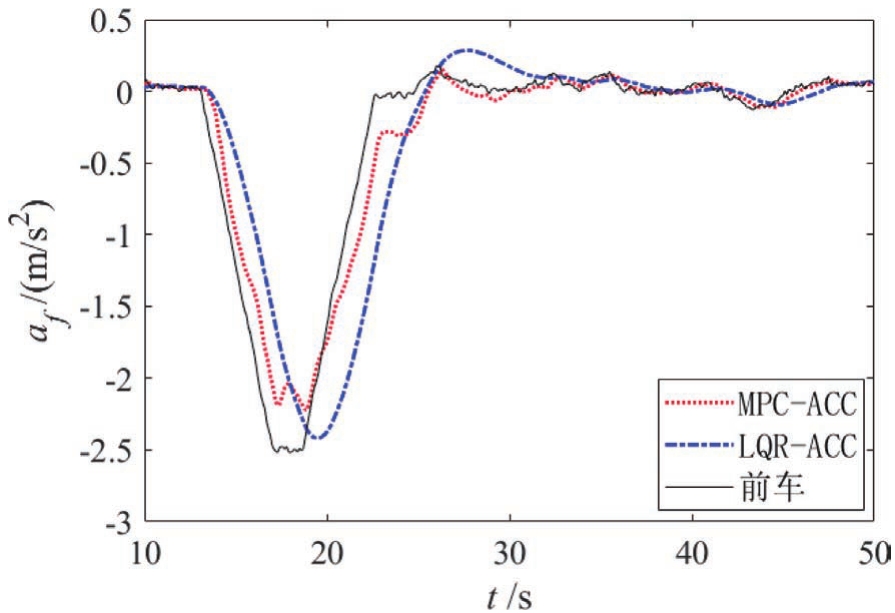
图12 前车急减速工况加速度曲线
本文基于模拟驾驶数据,建立了驾驶人跟车模型,考虑前车加速度的扰动,研究了基于GP的前车加速度在线预测方法,设计了基于MPC和驾驶人跟驰行为的拟人化ACC算法。研究结论如下:①根据驾驶数据所建立的驾驶人跟驰模型和敏感度模型可以真实反映驾驶人的跟驰特性,增加ACC的舒适度和用户满意度;②基于GP算法的前车加速度在线预测模型可以准确地反映前车加速度的变化趋势,有助于MPC预测模型的准确构建;③与传统的LQR-ACC相比,融合了驾驶人跟驰模型和前车加速度在线预测模型的MPC-ACC可以提升其跟踪性能和舒适性。
[1]罗莉华,龚李龙,李平,等.考虑驾驶员行驶特性的双模式自适应巡航控制设计[J].浙江大学学报(工学版),2011,45(012):2073-8.
[2]韩向敏,鲍泓,梁军,等.一种基于深度强化学习的自适应巡航控制算法[J].计算机工程,2018,v.44;No.489(07):38-41+7.
[3]张亮修,吴光强,郭晓晓.车辆自适应巡航控制系统的建模与分层控制[J].汽车工程,2018,v.40;No.286(05):50-6.
[4]MEMON Z A,PATHAN D M,HUSSAIN T.Analysis of an ACC System for Sliding Mode and MPC under Transitional Manoeuvers[J].Mehran University Research Journal of Engineering and Technology,2012,31(4):669-674.
[5]章军辉,李庆,陈大鹏.仿驾驶员多目标决策自适应巡航鲁棒控制[J].控制理论与应用,2018,v.35(06):50-8.
[6]AKHEGAONKAR S,LYDIE,GLASER,et al.Smart and Green ACC:Energy and Safety Optimization Strategies for EVs[J].IEEE Transactions on Systems Man & Cybernetics Systems,2017,48(99):142-53.
[7]TAC K V,DE A J,NAUS G,et al.Predictive Cruise Control in Hybrid Electric Vehicles[J].Predictive Cruise Control in Hybrid Electric Vehicles Tno Repository,2009,3(1):1.
[8]VAJEDI M,AZAD N L.Ecological Adaptive Cruise Controller for Plug-In Hybrid Electric Vehicles Using Nonlinear Model Predictive Control[J].IEEE Transactions on Intelligent Transportation Systems,2015,17(1):113-22.
[9]LI S,LI K,RAJAMANI R,et al.Model Predictive Multi-Objective Vehicular Adaptive Cruise Control[J].IEEE Transactions on Control Systems Technology,2011,19(3):556-66.
[10]陈涛,罗禹贡,韩云武,等.智能混合动力电动车辆多目标自适应巡航控制方法[J].清华大学学报(自然科学版),2013,053(010):1486-91.
[11]高振海,严伟,李红建,等.基于模拟驾驶员多目标决策的汽车自适应巡航控制算法[J].汽车工程,2015,(06):59-65.
[12]解来卿,罗禹贡,李升波,等.分布式电驱动车辆的ACC协同控制[J].汽车工程,2018,(6):652-8.
[13]吴光强,郭晓晓,张亮修.汽车自适应巡航跟车多目标鲁棒控制算法设计[J].哈尔滨工业大学学报,2016,48(1):80-6.
[14]GAO B,CAI K,QU T,et al.Personalized Adaptive Cruise Control Based on Online Driving Style Recognition Technology and Model Predictive Control[J].IEEE Transactions on Vehicular Technology,2020,PP(99):1.
[15]MESBAH,ALI.Stochastic Model Predictive Control:An Overview and Perspectives for Future Research[J].IEEE Control Systems Magazine,2016,36(6):30-44.
[16]戴旭彬,孙涛,夏维.基于MPC的自适应巡航算法改进研究[J].机电工程,2018,035(006):644-8,57.
[17]GU J, YI K. Adaptive cruise control algorithm design based on human drivers' driving pattern[J]. Journal of the Korean Society of Automotive Engineers Spring/Autumn Conference, 2005.
[18]GAZIS D C,HERMAN R,POTTS R B.Car-following theory of steady-state traffic flow using time-to-collision[J].Operations Research,2012,7(4):499-505.
[19]李升波.车辆多目标协调式自适应巡航控制[D].北京:清华大学,2009.