




郄天琪,王伟达,杨超,张宇航,刘文婕,李颖
北京理工大学
【摘要】 轨迹规划是智能车辆的核心技术之一,为提高车辆轨迹规划的性能,本文提出了一种考虑车辆运动约束的基于模型预测控制的智能车辆轨迹算法。首先,建立了智能车辆模型和障碍物模型 ; 在此基础上将建立基于智能车辆模型的线性预测模型,并用于预测未来状态。同时基于障碍物模型和车辆运动约束设计控制输入约束和输出变量约束,进行轨迹规划 ; 最终,通过仿真对本文提出的轨迹规划算法进行了验证。结果表明该方法可适用于静态和动态场景,并且所规划的轨迹较为平滑,有效提高了车辆行驶的安全性、稳定性和舒适性。
【关键词】 路径规划,轨迹规划,智能车辆,模型预测控制
A Path Planning Method for Intelligent Vehicles Based on Model Predictive Control Method
Qie Tianqi, Wang Weida, Yang Chao, Zhang Yuhang, Liu Wenjie, Li Ying
Beijing Institute of Technology
Abstract: Trajectory planning is one of the cores of intelligent vehicles.In order to improve the performance of vehicle trajectory planning, an intelligent vehicle trajectory algorithm based on model predictive control(MPC)considering vehicle motion constraints is proposed.Firstly, the intelligent vehicle model and obstacle model are established.On this basis, a linear prediction model based on the vehicle model will be established and used to predict the future state.At the same time, control input constraints and output variables constraints are designed based on obstacle model and vehicle motion constraints.Finally, the proposed trajectory planning algorithm is verified by simulation.The results show that the method can adapt to static and dynamic scenes.The planned trajectory is smooth.The safety, stability, and comfort of vehicle driving are improved.
Key words: path planning, trajectory planning, intelligent vehicles, model predictive control
随着人工智能、环境感知等相关技术的快速发展,智能车辆正处于由辅助驾驶转变为完全自动驾驶的阶段 [1] 。轨迹规划是智能车辆的核心技术之一。为实现完全自动驾驶,轨迹规划算法需要能够应对各种复杂场景。如何设计轨迹规划算法,规划出一条无碰撞路径,同时保证车辆运动的安全性、稳定性和舒适性,已成为当前智能车辆领域的研究热点。
许多学者采用规则式方法进行车辆轨迹规划,基于规则的方法根据行驶规则、知识、经验等建立行为规则库,根据不同的环境信息划分状态,按照规则逻辑确定智能车辆行驶轨迹 [2] 。BOSS无人车应用有限状态机方法(Finite State Ma-chine,FSM),车辆的驾驶状态由FSM的状态确定,事件作为引发状态迁移的输入条件控制当前状态沿转换路径跳转到另外的驾驶状态 [3] 。中国科学技术大学的智能先锋II采用层次状态机方法,把状态进行了分类,定义了高层次状态和低层次状态,降低了系统的维护难度 [4] 。基于规则的方法能够有效应对部分典型车辆行驶场景,不过其受限于规则库,由于添加场景有限,导致无法处理未添加到规则库的行驶场景。为处理一般场景,图搜索方法被用于轨迹规划,图搜索方法根据环境建立栅格地图,确定每个栅格的状态,依据这些状态进行路径搜索。其中,D算法是一种广度优先算法,其通过辐射状搜索周围节点,确定图中所有节点到初始节点的最短距离 [5] 。其穷举了所有可能的路径,能够一次性获得起始点到多个目标点的最优路径,但其搜索速度较慢,实时性差 [6] 。为了提高算法的实时性,A*算法被提出,其在搜索过程中增添了启发值,引导算法朝着期望的方向进行搜索 [7] 。基于快速随机搜索树的方法也被广泛用于轨迹规划,快速随机搜索树算法从起始点开始,随机选取一个方向,并在此方向上延伸一定距离,到达下一节点 [8] 。由于随机树在采样空间中随机采样,导致该算法实时性低,在动态环境中适应性较差,并且生成的轨迹在用于行驶过程中时舒适性较差 [9] 。许多学者提出了改进方案,如结合A*算法对随机树的扩张方向进行引导,使随机树的扩张具有指向性,提高实时性 [10] 。基于数值优化的方法也被用于轨迹规划,其根据车辆行驶需求,建立相关约束和评价指标,通过数值优化求解得到一条最优或较优的路径。人工势场法是一种典型的数值优化方法。其模拟电子在势场中的运动,引入斥力和引力,在需要规划的环境中建立一种虚拟势场。环境中的障碍物和道路边缘等产生斥力,目标点产生引力,车辆在虚拟势场中总是沿势能降低最快的方向移动,生成所规划的路径 [11] 。模型预测控制(Model Predictive Control,MPC)方法也是一种数值优化方法,其根据已知模型和当前状态量输出,根据预测轨迹与期望轨迹的偏差,施加控制量输入,同时可施加输入约束,从而保证车辆能够满足相应的运动约束,并且避免碰撞 [12] 。因此本文基于MPC方法提出了一种考虑车辆运动约束的轨迹规划算法,具体如下。
本文首先建立车辆和障碍物模型,并基于该车辆模型建立MPC中的线性预测模型,同时结合MPC能够显示表示约束的特点,考虑车辆的运动约束以及避开障碍物需满足的约束条件,提出基于MPC的轨迹规划算法。
首先建立单轨车辆运动学模型和障碍物模型,分别用于描述自动驾驶车辆和障碍物的状态。
本文采用单轨模型描述车辆,如图1所示。该模型进行了如下理想化假设 [13] :①忽略车辆垂向运动;②忽略车辆的悬架特性;③忽略轮胎横、纵向耦合关系;④不考虑轮胎的横向载荷转移,以及认为轮距相对于转弯半径可以忽略不计,使用单轨模型来描述车辆;⑤忽略空气阻力。该模型中各个状态量的更新公式如下:
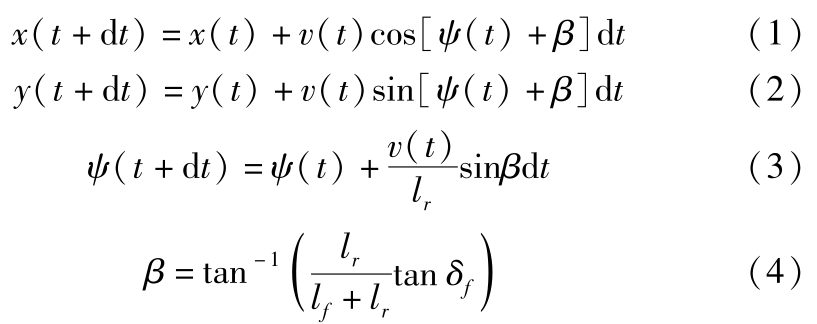
式中, x 和 y 是车辆纵向和横向位置; ψ 是车辆航向角; l f 和 l r 分别是质心和前轴以及后轴之间的距离; δ f 是前轮转角; t 是当前时间;d t 是采样时间; β 为质心侧偏角。
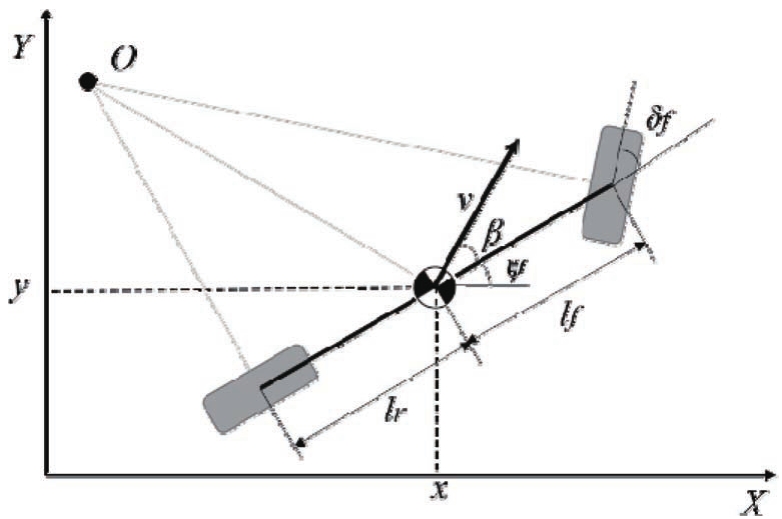
图1 车辆单轨模型示意图
考虑车辆的行驶过程,其中最常见的障碍物为其他车辆,因此本文根据车辆形状建立障碍物模型,如图2所示。其形状采用接近一般车辆的长方形表示,并将其周围一定范围设定为安全距离。障碍物状态可表示为
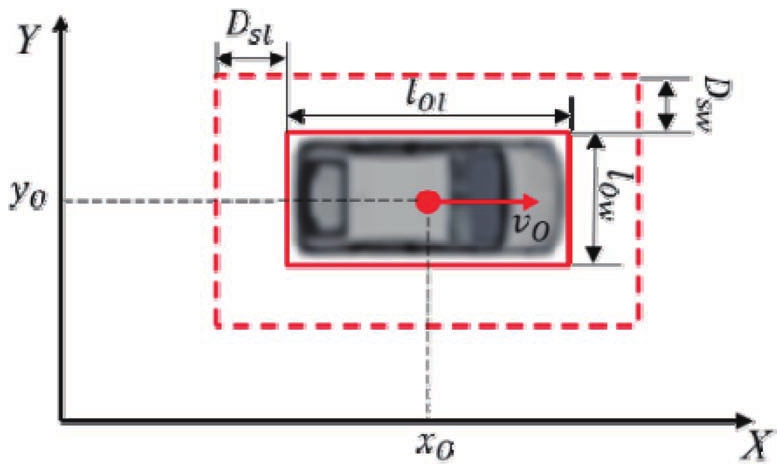
图2 障碍物模型示意图
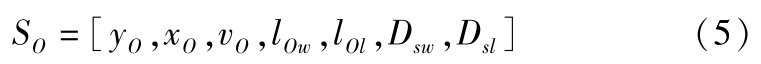
式中, y O 为障碍物横向位置; x O 为障碍物纵向位置; v O 为障碍物的运动速度; l Ow 为障碍物的横向宽度; l Ol 为障碍物的纵向长度; D sw 为横向安全距离; D sl 为纵向安全距离。
本节介绍基于MPC的路径规划算法,如图3所示。首先通过环境感知模块获取车辆周围的障碍物信息、车辆运动状态,通过全局路径规划模块获得参考轨迹。基于设计的轨迹规划算法得出速度和转角,传递到轨迹跟踪控制模块中,完成自动驾驶车辆的轨迹规划。
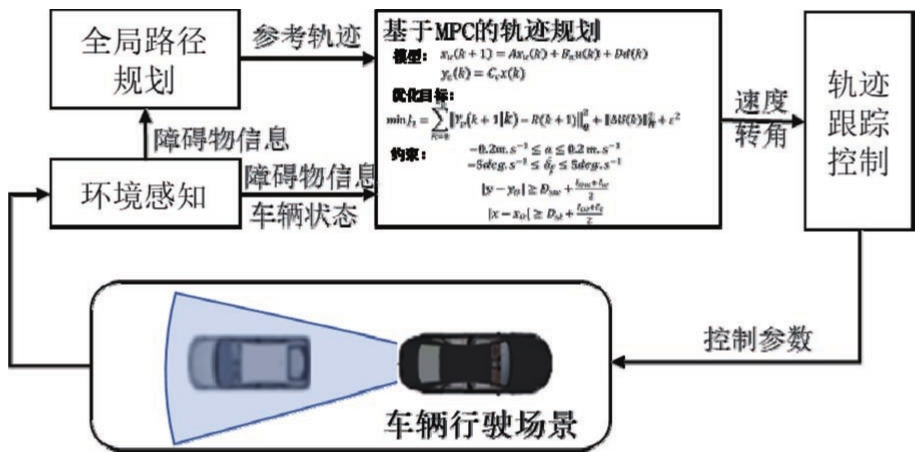
图3 轨迹规划算法示意图
基于单轨模型,即式(1)~式(4),建立当前采样时刻的线性预测模型如下:
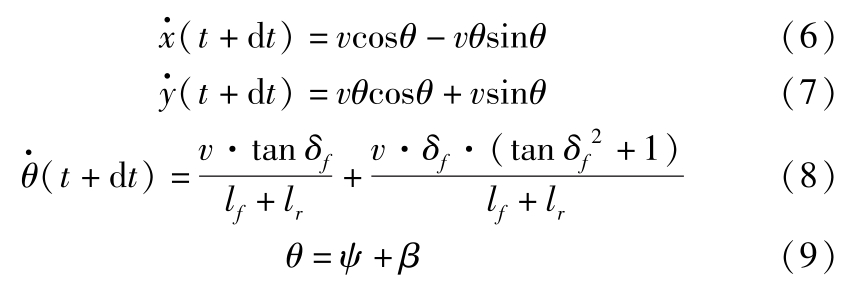
建立考虑线性离散时间系统下的状态空间模型:
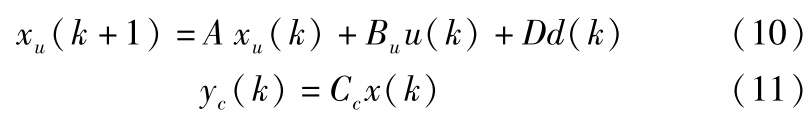
式中, x u ( k )∈R 4 是状态变量; u ( k )∈R 2 是控制输入变量; d ( k )为外部干扰变量; y c ( k )∈R 2 是被控输出变量。

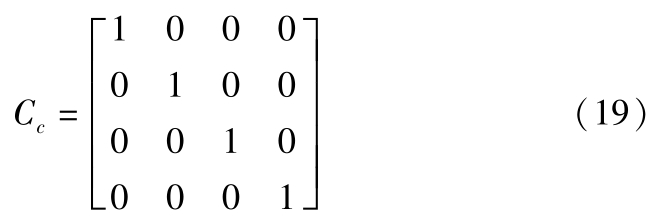
首先基于状态空间模型预测系统的未来动态,首先将式(10)和式(11)改写为增量模型如下:
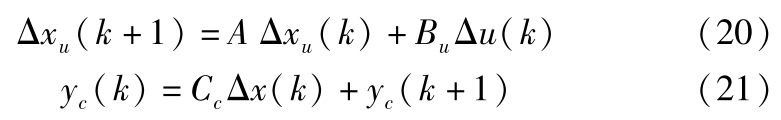
其中:
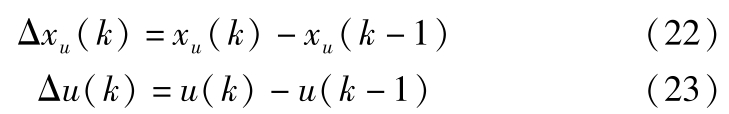
设预测时域为 p ,控制时域为 m , m 步输入向量和预测输出向量如下:
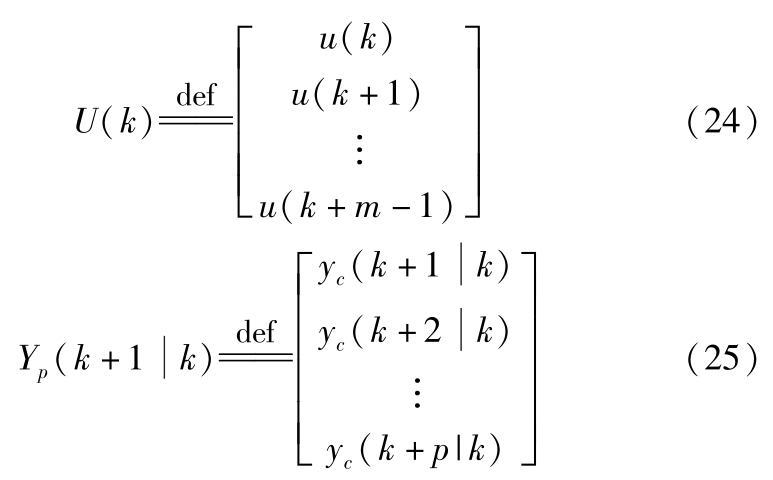
未来 p 步的预测方程为
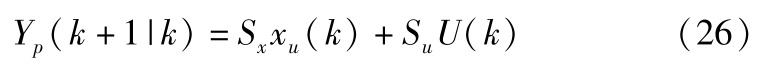
其中:
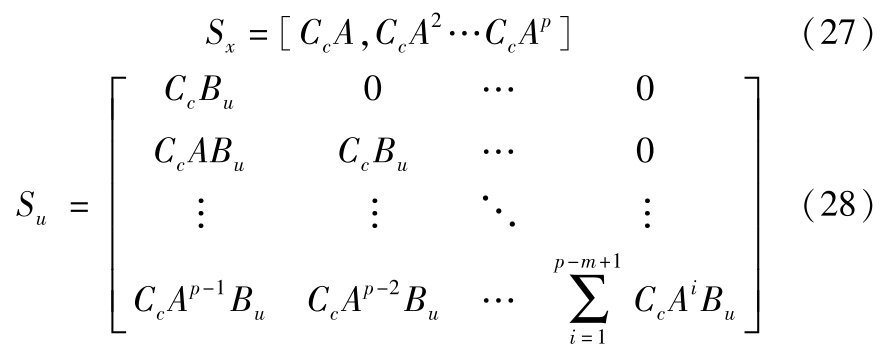
车辆需沿全局路径规划得出的路径行驶,优化求解的目标函数为
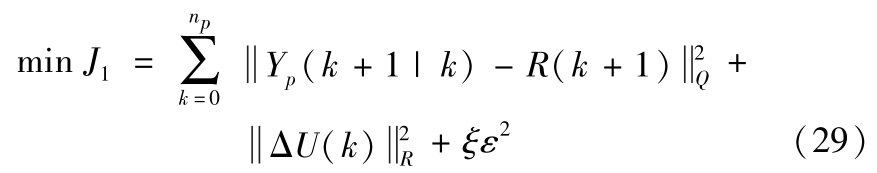
式中, ξ 为权重系数; ε 为松弛因子; Q 和 R 分别为输出误差与控制输入的加权矩阵; R ( k +1)为参考路径,即全局路径规划得出的路径,如下:
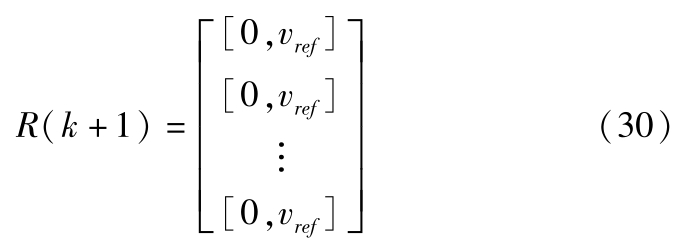
式中, v ref 为参考速度。
为保证规划轨迹的可行性,控制输入需满足的约束如下:

为避免与障碍物发生碰撞,被控输出变量需满足的约束如下:
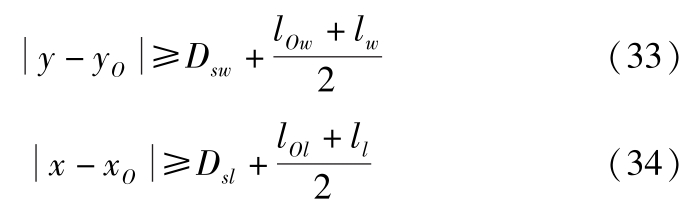
式中, l w 为主车宽度; l l 为主车长度。
为验证本文提出的基于自适应MPC的轨迹规划方法的性能,在MATLAB中搭建了两种典型场景,进行仿真试验。试验场景分别为避让静态障碍物和避让动态障碍物,如图4所示,主要包括自车和障碍物,自车根据自身以及障碍物的运动状态,应用本文提出的方法进行轨迹规划,最终得出避障轨迹。该试验中基本参数见表1。
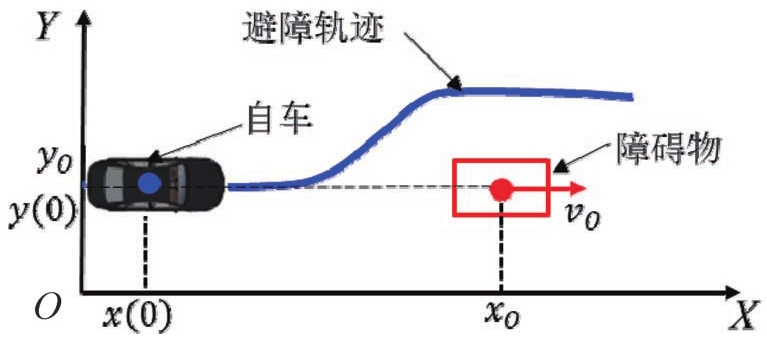
图4 车辆避障场景
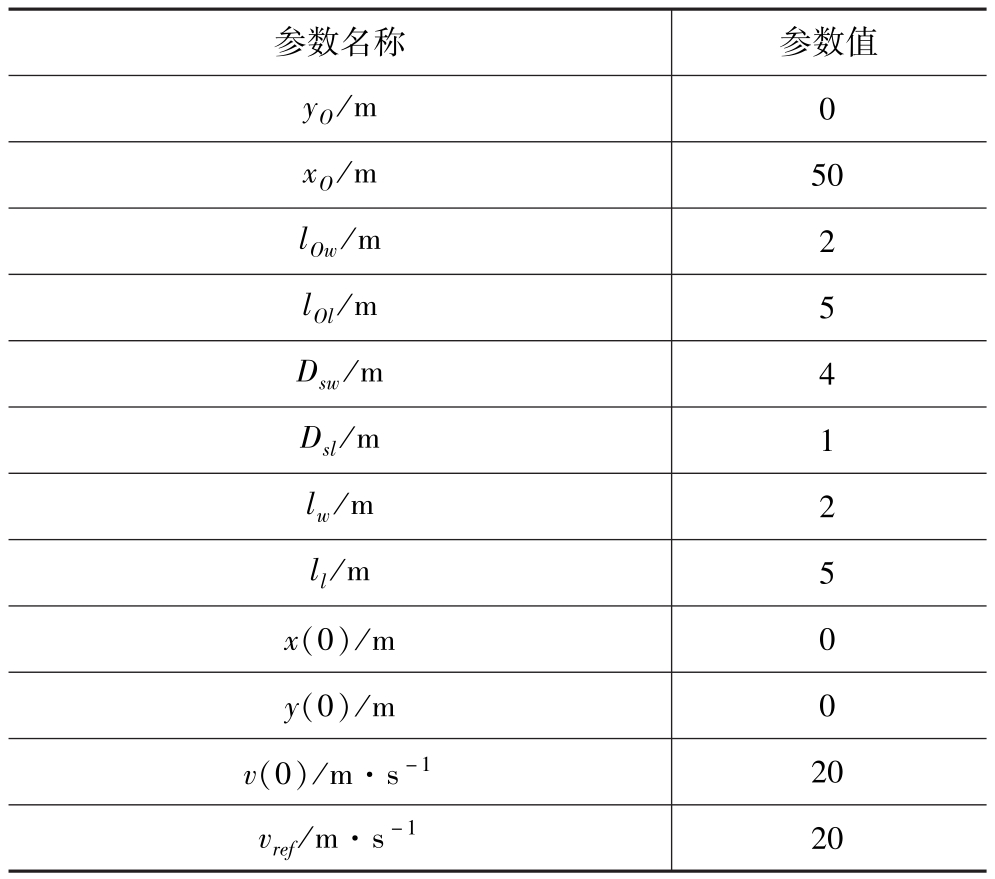
表1 仿真试验参数
避让静态障碍物场景下将障碍物的速度设置为0,即:

经仿真试验验证,主车能够避开障碍物,所规划的轨迹如图5所示。
车辆避障过程中与障碍物的相对距离如图6所示。在2.54s时主车与障碍物的纵向间距为0,此时横向间距为6.13m,能够有效保证车辆的行驶安全。
主车行驶过程中的速度如图7所示,车辆速度在避障过程中减慢,最低速度为19.33m·s -1 ,在避开障碍物后车辆会逐渐加速。车辆航向角如图8所示,在避障过程中始终保持在±10°之间,规划的路径较为平滑,且速度变化平缓。
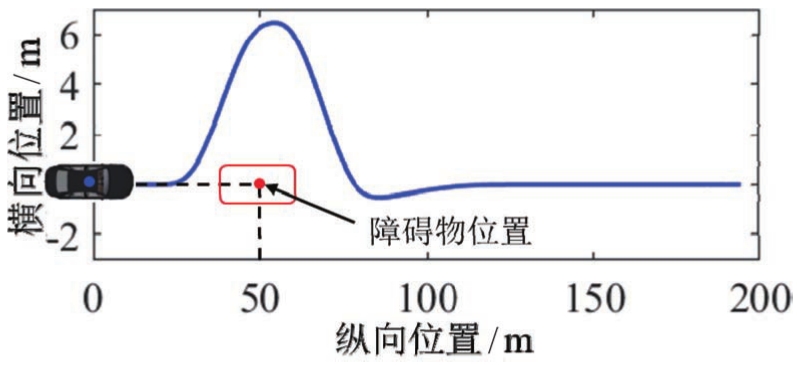
图5 静态障碍物场景中主车避障轨迹
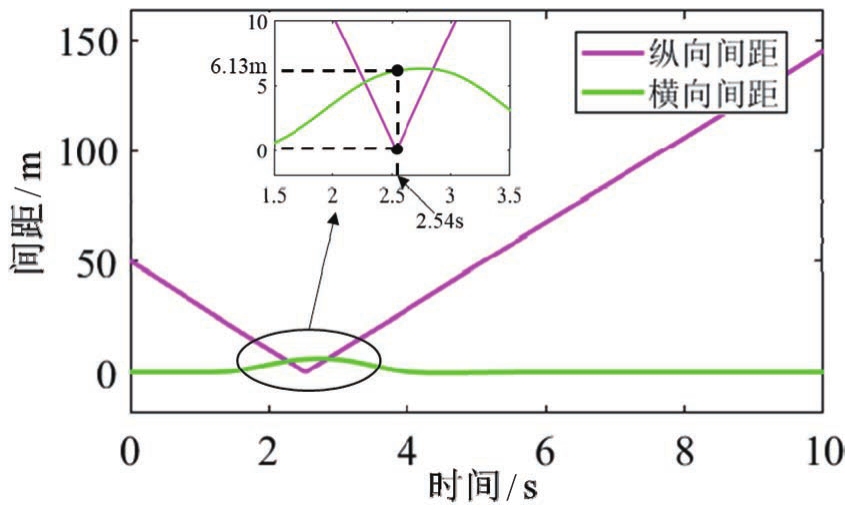
图6 静态障碍物场景中主车和障碍物间距
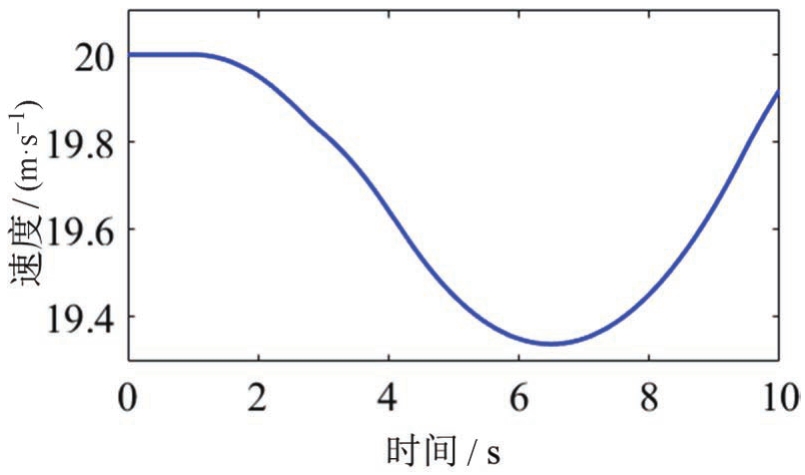
图7 静态障碍物场景中车辆速度
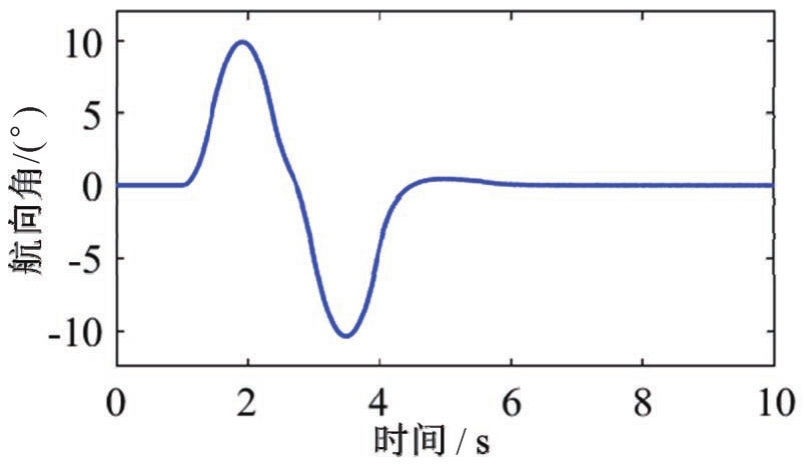
图8 静态障碍物场景中车辆航向角
避让动态障碍物场景下将障碍物的速度设置为10m·s -1 ,即:

经仿真试验验证,主车能够避开障碍物,所规划的轨迹如图9所示。
车辆避障过程中与障碍物的相对距离如图10所示。在5.08s时主车与障碍物的纵向间距为0,此时横向间距为5.08m,能够有效保证车辆的行驶安全。
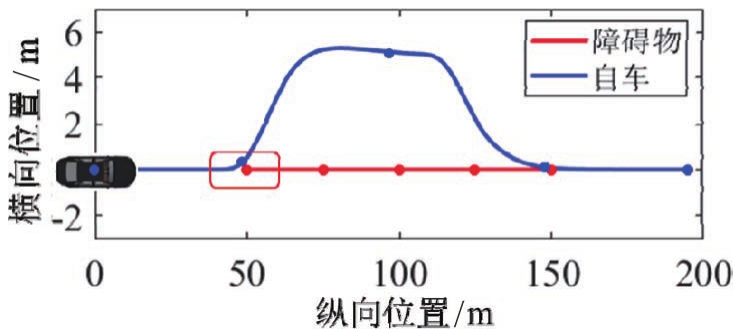
图9 静态障碍物场景中车辆速度
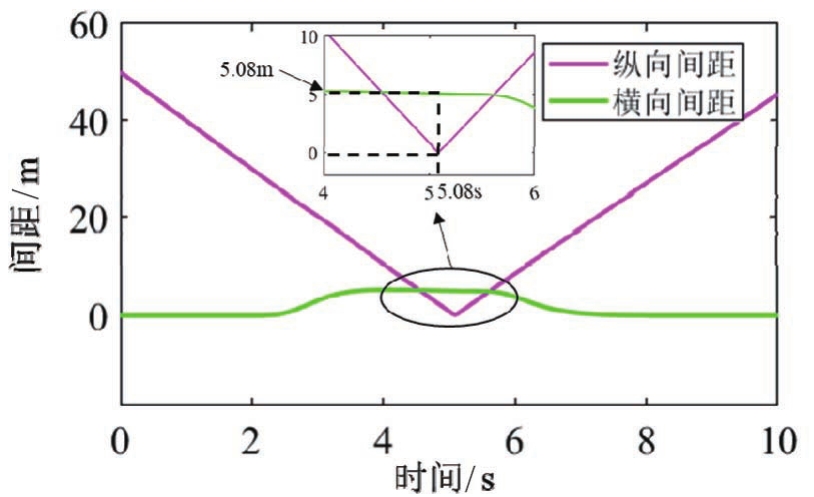
图10 动态障碍物场景中主车和障碍物间距
主车行驶过程中的速度如图11所示,车辆速度在避障过程中减慢,最低速度为19.22m·s -1 ,在避开障碍物后车辆会逐渐加速。车辆航向角如图12所示,在避障过程中始终保持在±10°之间。在动态场景下规划的轨迹较为平滑,且速度变化平缓。
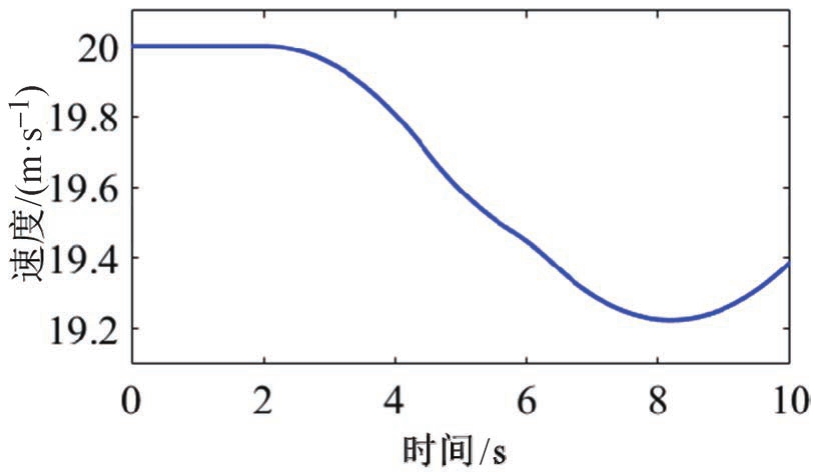
图11 动态障碍物场景中车辆速度
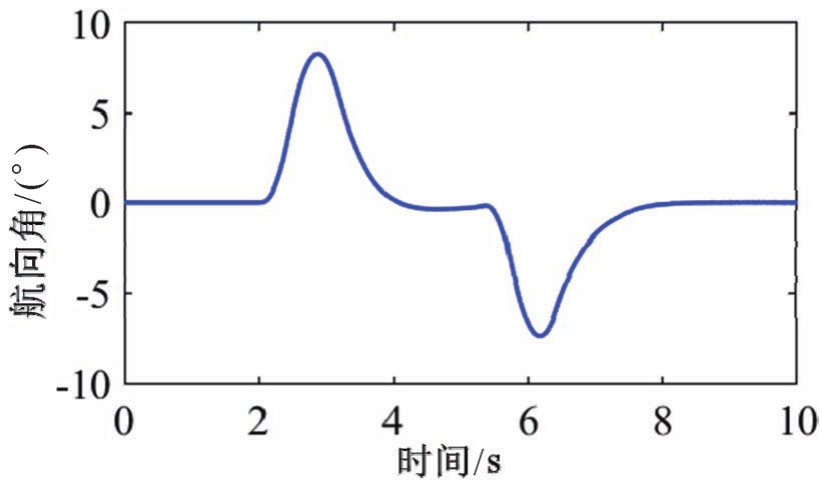
图12 动态障碍物场景中车辆航向角
本文提出了一种基于MPC的轨迹规划算法,将车辆需满足的运动约束和避障条件进行显式表达。仿真结果显示,本文提出的规划算法能够在较高行驶速度下规划出行驶轨迹,与静态障碍物和动态障碍物均能保持安全距离。并且,该算法所规划的轨迹较为平滑,且符合车辆的运动约束,便于进行跟踪控制。因此,本文提出的轨迹方法能够满足车辆行驶的安全性、稳定性和舒适性要求。
[1]WANG Y,LIU Z,ZUO Z.Trajectory Planning and Safety Assessment of Autonomous Vehicles Based on Motion Prediction and Model Predictive Control[J].IEEE transactions on vehicular Technology 2019, 68(9):8546-8556.
[2]杜明博.基于人类驾驶行为的无人驾驶车辆行为决策与运动规划方法研究[D].合肥:中国科学技术大学,2016.
[3]URMSON C,ANHALT J,BAGNEL D.Autonomous Driving in Urban Environments: Boss and the Urban Challenge[J].Journal of Field Robotics, 2008, 25(8): 425-466.
[4]黄璐.基于本体论的无人驾驶车辆场景评估与行为决策方法研究[D].合肥中国科学技术大学,2019.
[5]GONZÁLEZ D,PÉREZ J,MILANÉS V, A Review of Motion Planning Techniques for Automated Vehicles[J].IEEE Transaction on Intelligent Transportation Systems, 2016,17(4):1135-1145.
[6]JOYOUNG L,BYUNGKYU P.Development and Evaluation of a Cooperative Vehicle Intersection Control Algorithm Under the Connected Vehicles Environment[J].IEEE Transaction on Intelligent Transportation Systems, 2012, 13(1):81-90.
[7]YOON S,YOON S E,LEE U,et al.Recursive Path Planning Using Reduced States for Car-Like Vehicles on Grid Maps[J].IEEE Transaction on Intelligent Trans portation Systems, 2015, 16(5):2797-2813.
[8]周维,过学迅,裴晓飞.基于RRT与MPC的智能车辆路径规划与跟踪控制研究[J].汽车工程,2020,42(9):1151-1158.
[9]朱冰,韩嘉懿,赵健.基于安全场改进RRT*算法的智能汽车路径规划方法[J].汽车工程,2020,42(9): 1145-1150.
[10]冯来春,梁华为,杜明博.基于A*引导域的RRT智能车辆路径规划算法[J].计算机系统应用,2017,26(8): 127-133.
[11]RASEKHIPOUR Y,KHAJEPOUR A,CHEN S.A Potential Field-Based Model Predictive Path-Planning Controller for Autonomous Road Vehicles[J].IEEE Transaction on Intelligent Transportation Systems, 2017, 18(5):1255-1267.
[12]GUO H,SHEN C,ZHANG H.Simultaneous Trajectory Planning and Tracking Using an MPC Method for Cyber-Physical Systems: A Case Study of Obstacle Avoidance for an Intelligent Vehicle[J].IEEE Transactions on Industrial Informatics, 2018, 14(9):4273-4283.
[13]DIXIT S,MONTANARO U,DIANATI M.Trajectory Planning for Autonomous High-Speed Overtaking in Structured Environments Using Robust MPC[J].IEEE Transaction on Intelligent Transportation Systems, 2020, 21(6):2310-2323.