




在微观世界中,所谓全同粒子是指内禀性质完全相同的同类粒子,例如电子。所有电子的质量(静止质量都等于1 a.u.,1 a.u.=9.109 1×10 -28 g)、电荷(电荷都等于1 a.u.,1 a.u.=4.802 98×10 -10 esu)、自旋(自旋量子数 s =1/2,为半整数)等固有性质完全相同,所以,电子是全同粒子。包含全同粒子的体系称为全同粒子体系。一个原子或一个分子中的所有电子就组成一个全同粒子体系。
由于全同粒子的内禀性质完全相同,无法借助内禀性质的差异区分它们。如前所述,由于测不准原理,全同粒子在运动过程中又是不可区分的。因而,从微观世界的基本特性——量子化特性和微观粒子的波粒二象性——着眼,全同粒子系中相互作用的粒子间本质上是不可分辨的。
既然全同粒子系中相互作用的粒子彼此是不可分辨的,那么交换其中的任意两个粒子的全部坐标(包括空间坐标和自旋坐标),或重新取名或重新编号,体系所处的状态是不会改变的;体系的任何可观测的物理量,特别是哈密顿(Hamilton)量也是不会改变的
[10-12]
。若用
q
i
(
i
=1,2,…,
i
,…,
N
)表示粒子
i
的全部坐标,波函数
Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
)表示全同粒子系的状态,
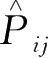 表示
i
粒子和
j
粒子的全部坐标的交换,那么,由于全同性,
表示
i
粒子和
j
粒子的全部坐标的交换,那么,由于全同性,
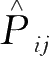 Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
)=
Ψ
(
q
1
,…,
q
j
,…,
q
i
,…,
q
N
)所描述的状态也应该是体系的同一状态。
Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
)=
Ψ
(
q
1
,…,
q
j
,…,
q
i
,…,
q
N
)所描述的状态也应该是体系的同一状态。
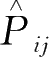 Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
)和
Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
)最多只能相差一个常数因子,即
Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
)和
Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
)最多只能相差一个常数因子,即
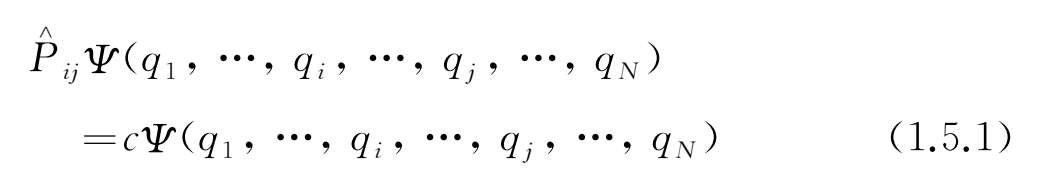
再用交换算符
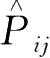 左乘上式的两边,则
左乘上式的两边,则
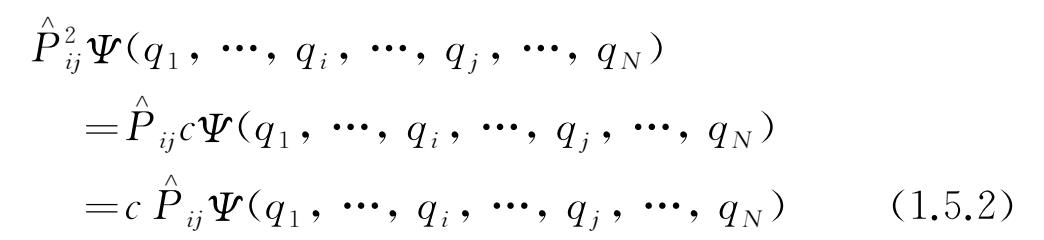
将(1.5.1)式代入,可得
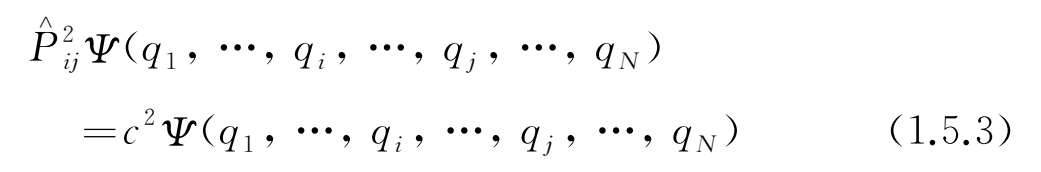
用
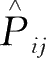 两次,相当于没有净作用,所以
两次,相当于没有净作用,所以
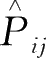 的平方是单位算符,即
的平方是单位算符,即
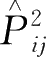 =1。于是有
=1。于是有


也就是说,算符
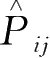 只有两个本征值。当
c
=+1,
只有两个本征值。当
c
=+1,
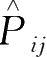 Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
)=
Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
),称此波函数
Ψ
为对称波函数;当
c
=-1,
Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
)=
Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
),称此波函数
Ψ
为对称波函数;当
c
=-1,
 Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
)=-
Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
),称此波函数
Ψ
为反对称波函数。
Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
)=-
Ψ
(
q
1
,…,
q
i
,…,
q
j
,…,
q
N
),称此波函数
Ψ
为反对称波函数。
换言之,全同粒子的不可分辨性,对体系的波函数施加了严格的限制。全同粒子系中对于任意的一对粒子的交换,要求体系的波函数要么是对称的,要么是反对称的,而且这一性质不随时间改变。量子力学中称此为全同性原理 [4] 。
实验表明,全同粒子系的波函数的交换对称性和粒子的自旋禀性相关。凡整数自旋( s =0,1,2,…)的粒子,体系波函数对于交换总是对称的。这类粒子称为玻色子(Bose子);而凡半整数自旋( s =1/2,3/2,…)的粒子,体系波函数对于交换总是反对称的,这类粒子称为费米子(Fermi子)。