力学公式参考一览表

400多年前，达·芬奇写道：“人类任何知识，如果不使用力学论据体系，都无法成为真理科学之一。”这是许多年前的真理，直到今天依然被证实是准确的。在这本书中，我们不止一次接触力学公式。我们为学过力学，但是已经忘记这些公式的读者列出一个简单的表格，用来回忆起它们（这些公式的原理可以在力学教科书上找到）。

我们现在举几个例子来说明这个表的用法。用匀速直线运动的速度v乘以时间t，得到了距离S（公式S=vt）。

用不变的力f乘以距离S，得到功A，功A还等于质量m乘以末速度v的平方的一半：A=FS=mv ² /2[公式A=FS只适用于力与距离的方向相同时。通常情况下，要使用更为复杂的公式A=FScosα，α表示力的方向与距离的方向之间的夹角。同样，公式A=mv ² /2也仅适用于物体的初速度等于零的简单情况下。如果初速度等于v0，末速度等于v，那么导致这种速度发生变化耗费的功就要用公式A=mv ² /2-mv ₀ ² /2表示。]

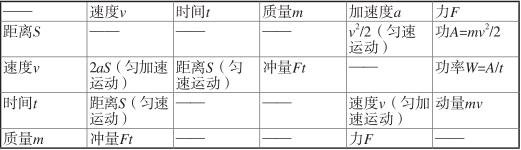
利用乘法表格我们可以找到相应的除法的结果。相同，从表中，我们也可以得出这样的关系：匀加速运动的速度v除以时间t，等于加速度a（公式a=v/t）。

力f除以质量m等于加速度a，除以加速度a等于质量m：

a=f/m和m=f/a

解答力学计算题的时候，需要计算加速度。你可以参照上面列表中所有包含加速度的公式。aS=v ² /2，v=at，F=ma，通过这些公式还能得出：t ² =2S/a，或者S=at ² /2。

在所有列出的公式中，找到适合解答问题的一个公式。

如果你想找到所有可以用来计算力的公式，以下这些公式还可以为你提供参考：

FS=A（功）

Fv=W（功率）

Ft=mv（动量）

F=ma

这里不能忽略的一点是，重量P也是力。因此在列出公式f=ma的同时也可以列出公式P=mg，在这里，g代表物体接近地面时的重力加速度。与之相同，从公式FS=A中也可以得出Ph=A，这个公式适用于当重量为P的物体升高高度为h的时候。

列表空格部分表示有关的量相乘不具有物理意义。 6d7up3KRR69nOVxbntc+ZZnUJFXtzU2TWCqe7YOSO3asyqHn/xmz+R4TzOWs3BOS