




上面测量河对岸松树高度的方法还有没有改进的空间呢?探索永无止境。既然是利用相似三角形的原理,能否借助镜子来测量呢?
将一面镜子放在测量者与要测量的松树之间,如图14所示,测量的人两眼看着镜子一步步地往后退,往后退的过程中要始终注视着镜子中松树的影子,一直退到在镜子里恰好能望到树梢A的点D的位置。根据光的反射定律可知,这时候树高AB是测量者身高ED的几倍,树根到镜子的距离BC就恰好是镜子到测量者的距离DC的几倍,为什么呢?
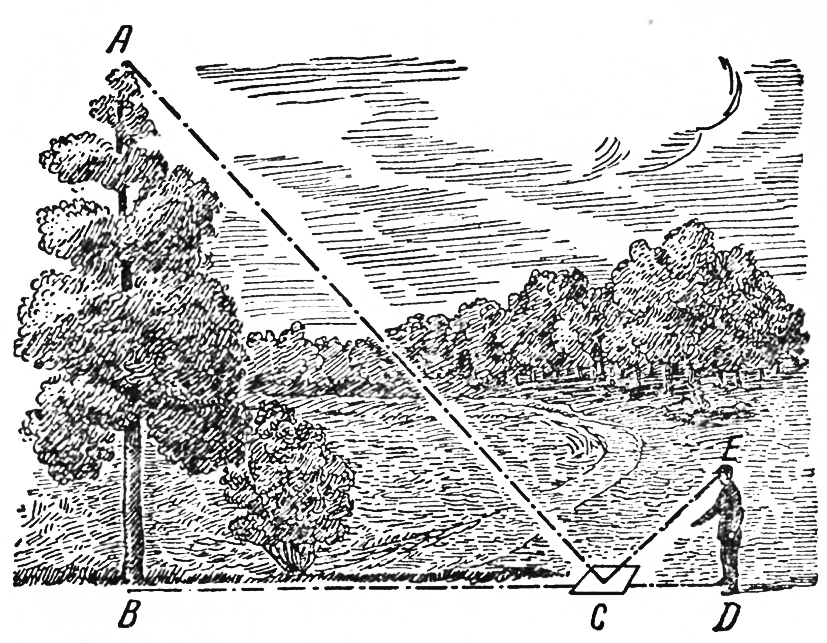
图14 利用镜子测高
为了将图14更详细地展现在各位面前,将镜子中的影像画出来,如图15所示,树梢A反映在点A'上,AB=A'B,从两个相似三角形BCA'和DCE可知:
A'B :ED=BC :DC
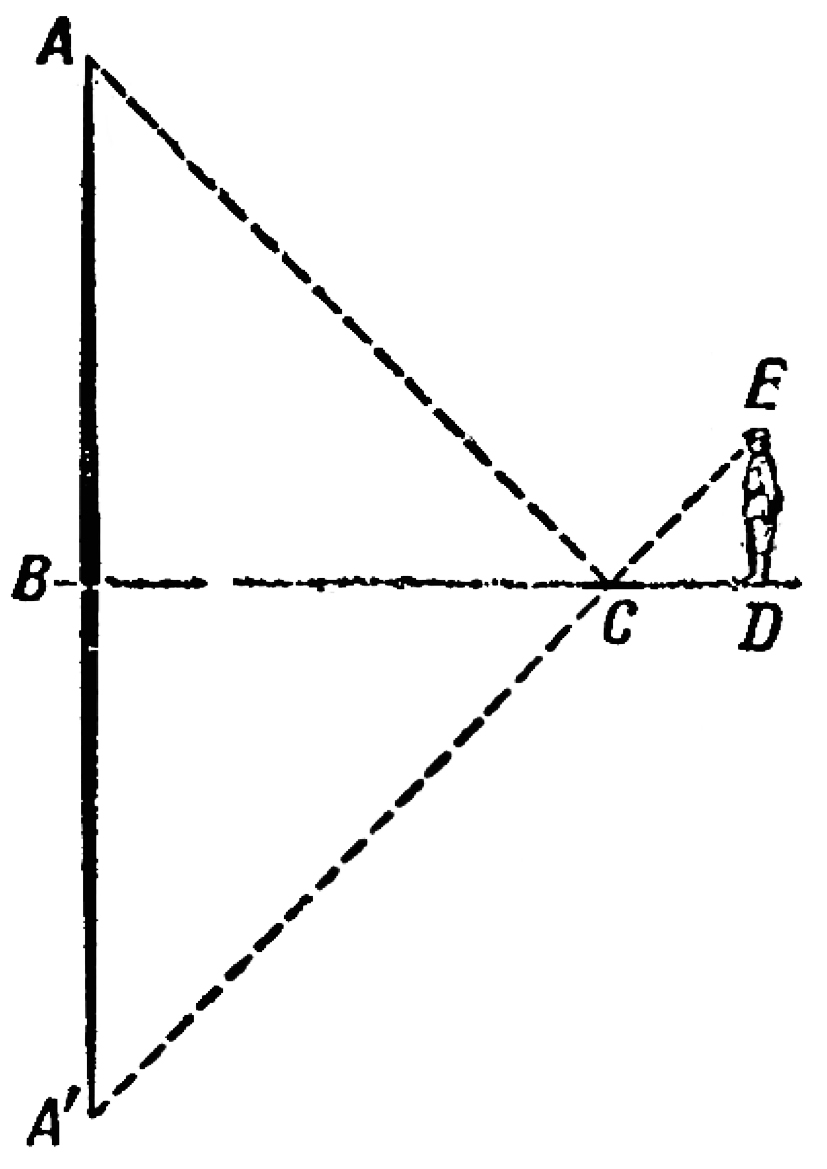
图15 用镜子测高的图解
现在,只要将公式中的A'B用同值的AB代替,就可以得出本题的答案了。
这种比较简单方便的方法只要借助一面平面镜在任何天气中都可以使用,但是对于大规模的树林而言则不适用,只适用于个别孤立的树。
上面的方法还能否进行改进呢?比如被测的松树由于某种原因不能接近,或者在河对岸,使用镜子还能够进行测量吗?
上面这个猜想的问题,早在几百年前就已经有人提出过了。一位中世纪的数学家安东尼·德·克雷蒙氏就在他的著作《实用土地测量》里讨论过。
解决这个问题,可以再次使用上面提到的镜子影像实物化的方法。将镜子放在两个地方测量,做出适当的图解,就不难从两个相似三角形推导出所测的树高等于测量者眼高乘以两个距离的比,一个距离就是两次放置镜子位置之间的距离,另一个就是两次测量的时候测量者和镜子之间的距离差。
在结束我们关于测量松树高度的讲述之前,还要再解答一个关于树林的计算题,这是一个新的知识点,一个新的几何知识。