




现在我们来看牛顿那一道关于牛吃草的题,刚才那道题正是以它为样本改编的。
其实,这道题也不是牛顿自己想出来的,而是人民大众进行数学探索的产物。
“三片牧场的草均匀地生长,它们的面积分别是:
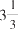 公顷,10公顷和24公顷。第一片牧场的草能供12头牛吃4周,第二片能供21头牛吃9周,第三片牧场能供多少头牛吃18周?”
公顷,10公顷和24公顷。第一片牧场的草能供12头牛吃4周,第二片能供21头牛吃9周,第三片牧场能供多少头牛吃18周?”
引入一个辅助的未知数y,用来表示1公顷草地一周的生长率(新长出的草占初始草量的比率)。第一片牧场一周的生长率为
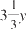 ,而4周后就是初始时1公顷草地草量的
,而4周后就是初始时1公顷草地草量的
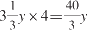 。这就好比原来的牧场扩大后变成了:
。这就好比原来的牧场扩大后变成了:
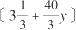
公顷。换句话说,牛吃掉了覆盖了
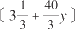 公顷的牧场的草。一周12头牛则吃了这么多草的四分之一,而一头牛一周则吃这么多草的
公顷的牧场的草。一周12头牛则吃了这么多草的四分之一,而一头牛一周则吃这么多草的
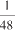
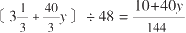 公顷。
公顷。
同样的方法,用给出的第二片牧场的数据来表示一头牛一周吃掉的草的面积:
1公顷草地1周新长出的草量=y
1公顷草地9周新长出的草量=9y
10公顷草地9周新长出的草量=90y
9周供21头牛吃的草所覆盖的面积为
10 + 90y
公顷,够一头牛一周吃的草的面积为
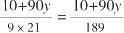
公顷。两种情况下牛吃草的速率应该相同:
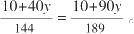
解方程,得
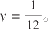
现在确定可供一头牛吃一周的草的面积:
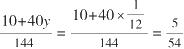
公顷。最后回到题目的问题。设牛的数量为x,得到:
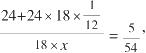
解得,x=36。第三片牧场可供36头牛吃18周。