




“大自然只使用最长的线来编织她的图景;因此,每根织线都能洞见整个大自然的锦绣图景。
Nature uses only the longest threads to weave her patterns, so that each small piece of her fabric reveals the organization of the entire tapestry.
——理查德·费曼(Richard P. Feynman)|美国理论物理学家|1918—1988”
◄ input() 函数接受一个标准输入数据,返回为字符串str类型 ◄ int() 将输入转化为整数 ◄ math.factorial() 计算阶乘 ◄ numpy.cumprod() 计算累计乘积 ◄ numpy.inner() 计算行向量的内积,函数输入为两个列向量时得到的结果为张量积 ◄ numpy.linalg.inv() 计算方阵的逆 ◄ numpy.linspace() 在指定的间隔内,返回固定步长的数组 ◄ numpy.math.factorial() 计算阶乘 ◄ numpy.random.seed() 固定随机数发生器种子 ◄ numpy.random.uniform() 产生满足连续均匀分布的随机数 ◄ numpy.sum() 求和 ◄ scipy.special.factorial() 计算阶乘 ◄ seaborn.heatmap() 绘制热图
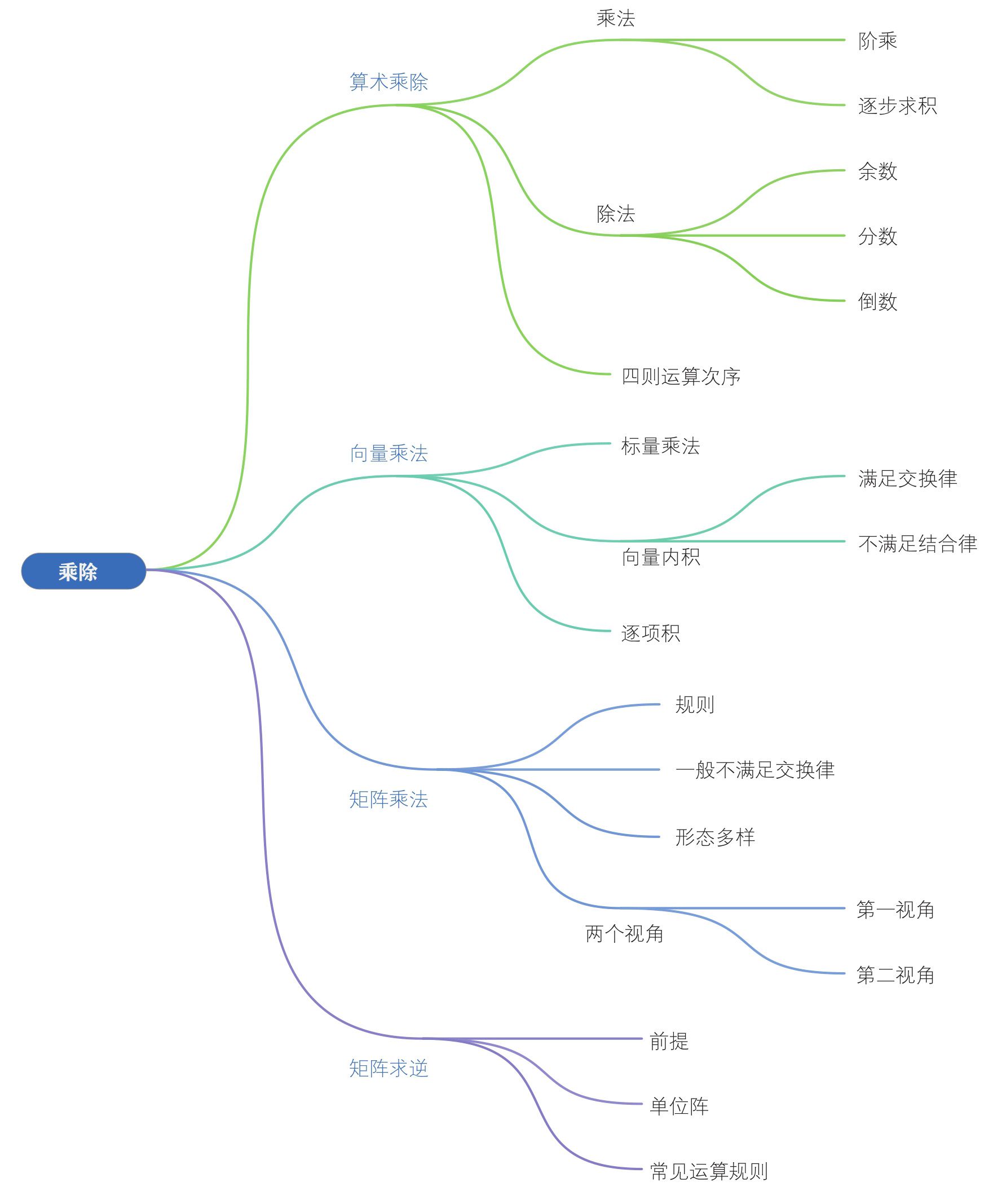

乘法 (multiplication)算式等号左端是 被乘数 (multiplicand)和 乘数 (multiplier),右端是 乘积 (product),如图2.1所示。乘法运算符读作 乘 (times或multiplied by)。 乘法表 (multiplication table或times table)是数字乘法运算的基础。

图2.1 乘法运算
图2.2所示为在数轴上可视化2×3=6。

图2.2 2×3=6在数轴上的可视化
介绍几个常用乘法符号。乘法符号×用于数字相乘,一般不用于两个变量相乘。而在线性代数中,×表示 叉乘 (cross product或vector product),完全是另外一回事。
在代数中,两个变量 a 和 b 相乘,可以写成 ab ;这种记法被称做 隐含乘法 (implied multiplication)。 ab 也可以写成 a · b 。
通常,圆点·不用在数字相乘,因为它容易和 小数点 (decimal point)混淆。线性代数中, a · b 表示 a 和 b 两个向量的 标量积 (scalar product),这是本章后续要介绍的内容。
多提一嘴,乘法计算时,请大家多留意数值单位。举个例子,正方形的边长为1 m,其面积数值可以通过乘法运算1×1=1获得,而结果单位为平方米(m 2 )。有一些数值本身 无单位 (unitless),如个数、Z分数。Z分数也叫 标准分数 (standard score),是概率统计中的一个概念,Z分数是一个数与平均数的差再除以标准差的结果。
与乘法相关的常用英文表达见表2.1。
鸢尾花书会在《统计至简》一册详细介绍Z分数这个概念。
表2.1 乘法相关英文表达

Bk3_Ch2_01.py完成两个数乘法。Python中两个数字相乘用*(asterisk或star)。
某个正整数的 阶乘 (factorial)是所有小于及等于该数的正整数的积。比如,5的阶乘记作5!,对应的运算为

特别地,定义0的阶乘为0!=1。本书有两个重要的数学概念需要用到阶乘——排列组合和泰勒展开。
Python中可以用math.factorial()、scipy.special.factorial()、numpy.math.factorial()计算阶乘。为了帮助大家理解,Bk3_Ch2_02.py自定义函数求解阶乘。
对于一组数字, 累计乘积 (cumulative product)也叫 累积乘积 ,得到的结果不仅仅是一个乘积,而是从左向右每乘一个数值得到的分步结果。比如,自然数1到10求累计乘积结果为
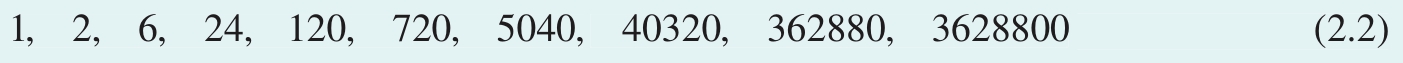
对应的累计乘积过程为

Bk3_Ch2_03.py利用numpy.linspace(1, 10, 10)产生1~10这十个自然数,然后利用numpy.cumprod()函数来求累计乘积。请大家自行研究如何使用numpy.arange(),并用这个函数生成1~10。
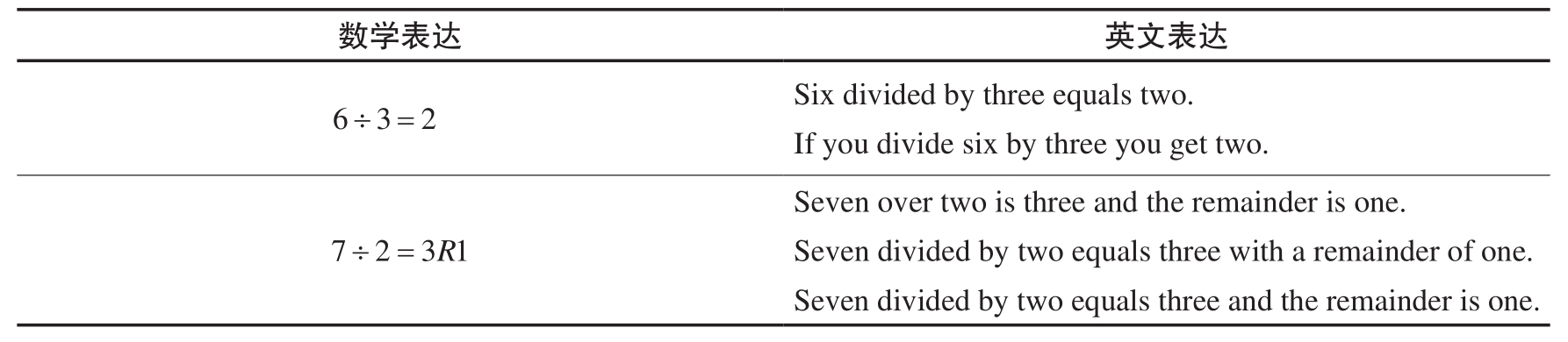
除法 (division)是 乘法的逆运算 (reverse operation of multiplication)。 被除数 (dividend或numerator) 除以 (over或divided by) 除数 (divisor或denominator)得到 商 (quotient),如图2.3所示。

图2.3 除法运算
除法运算有时可以 除尽 (divisible),如 6可以被3除尽 (six is divisible by three)。除法有时得到 余数 (remainder),如7除2余1。除法的结果一般用 分数 (fraction)或 小数 (decimal)来表达,详见表2.2。
表2.2 除法英文表达
Bk3_Ch2_04.py完成两个数的除法运算,除法运算符为正斜杠/。
Bk3_Ch2_05.py介绍如何求余,求余数的运算符为%。
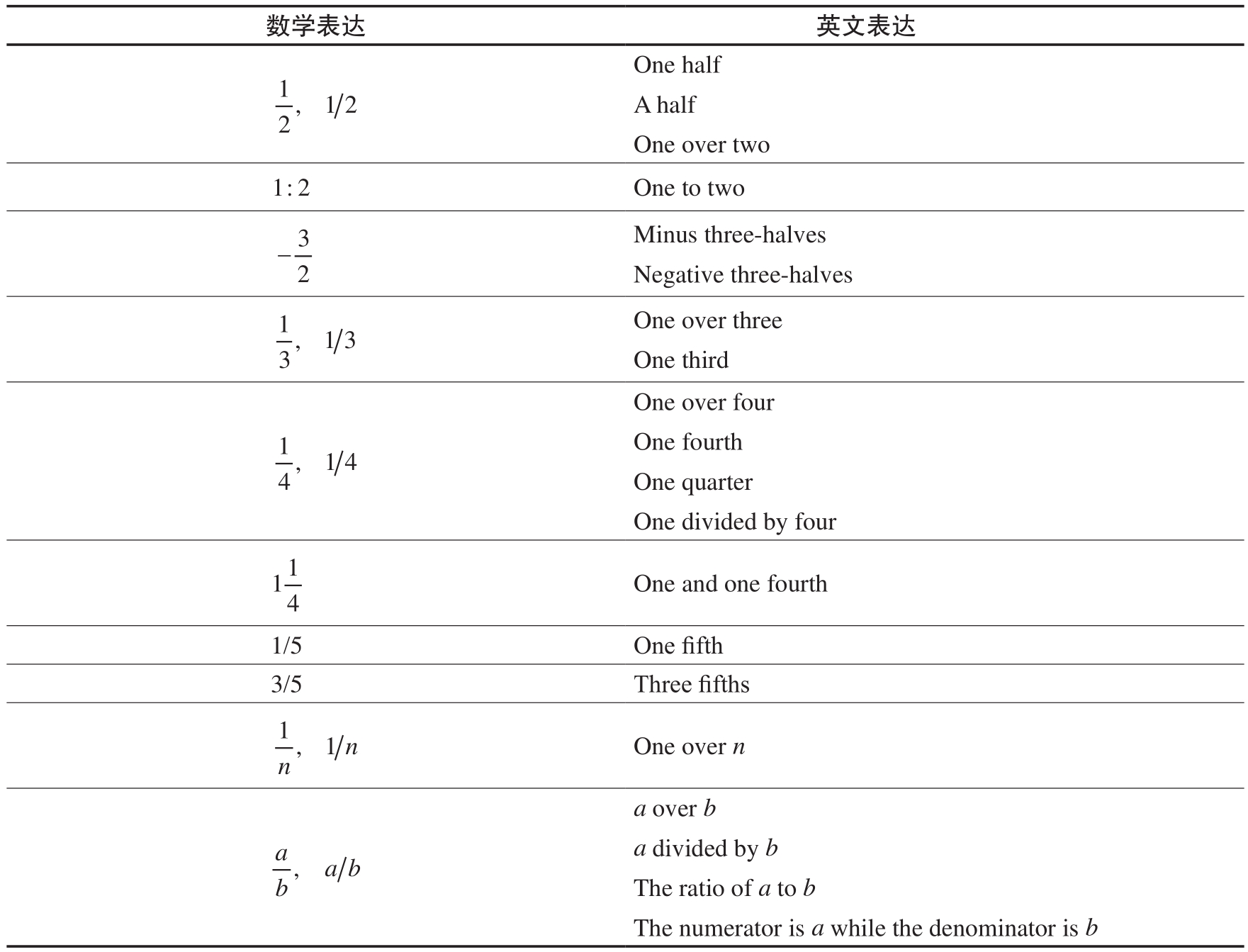
最常见的 分数 (fraction)是 普通分数 (common fraction或simple fraction),由 分母 (denominator)和 分子 (numerator)组成,分隔两者的是 分数线 (fraction bar)或 正斜杠 (forward slash)/。
非零整数 (nonzero integer) a 的 倒数 (reciprocal)是1/ a 。分数 b / a 的倒数是 a / b 。 a 、 b 均不为0。
表2.3中总结了常用分数英文表达。
表2.3 分数相关英文表达
这一节介绍三种重要的向量乘法:① 标量乘法 (scalar multiplication);② 向量内积 (inner product);③ 逐项积 (piecewise product)。
标量乘法运算中,标量乘向量的结果还是向量,相当于缩放。
标量乘法运算规则很简单,向量 a 乘以 k , a 的每一个元素均与 k 相乘,如下例标量2乘行向量[1, 2, 3]
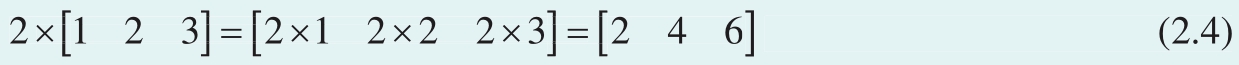
再如,标量乘列向量如

图2.4所示为标量乘法示意图。

图2.4 标量乘法
同理,标量 k 乘矩阵 A 的结果是 k 与矩阵 A 每一个元素相乘,比如
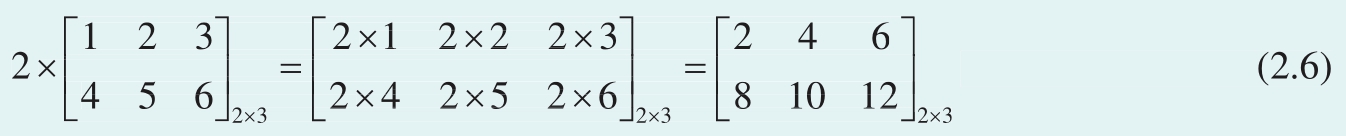
Bk3_Ch2_06.py完成向量和矩阵标量乘法。
向量内积 (inner product)的结果为标量。向量内积又叫 标量积 (scalar product)或 点积 (dot product)。
向量内积的运算规则是:两个形状相同的向量,对应位置元素一一相乘后再求和。比如,下例计算两个行向量内积

计算两个列向量内积,比如:
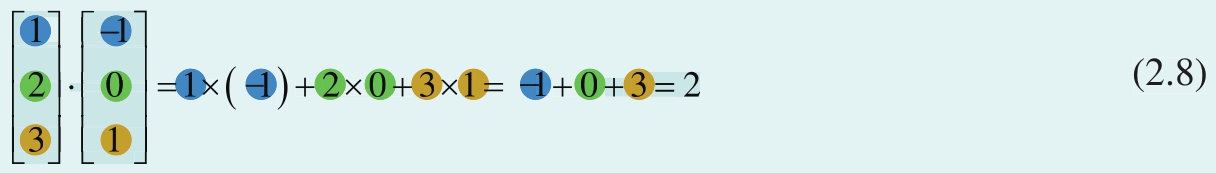
图2.5所示为向量内积规则的示意图。
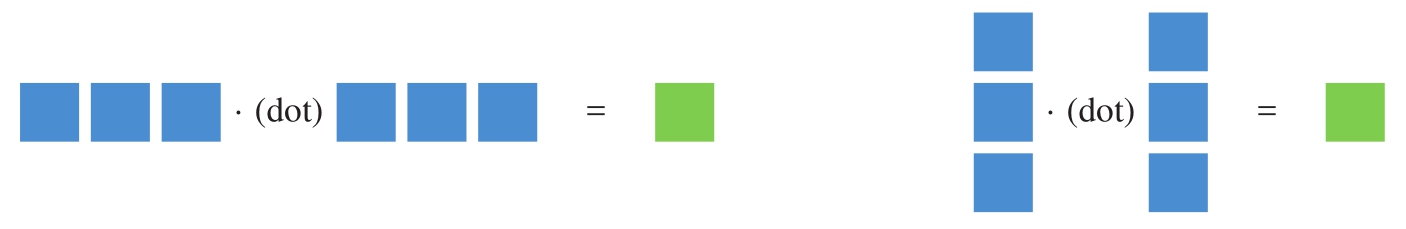
图2.5 向量内积示意图
显然,向量内积满足 交换律 (commutative),即

向量内积 对向量加法满足分配律 (distributive over vector addition),即

显然,向量内积不满足 结合律 (associative),即

Bk3_Ch2_07.py代码用numpy.inner()计算行向量的内积;但是,numpy.inner()函数输入为两个列向量时得到的结果为 张量积 (tensor product)。
机器学习和深度学习中,张量积是非常重要的向量运算,鸢尾花书将在《矩阵力量》一册中进行详细介绍。
下面举几个例子,让大家管窥标量积的用途。
给定以下五个数字,即

这五个数字求和,可以用标量积计算得到,即
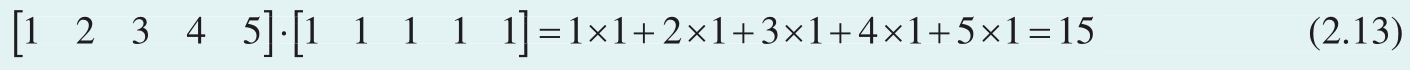
前文提过,[1, 1, 1, 1, 1] T 叫作全1向量。
这五个数字的平均值,也可以通过标量积得到,即

计算五个数字的平方和,有
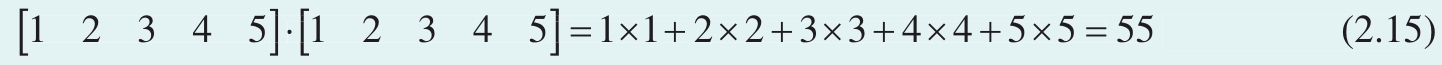
此外,标量积还有重要的几何意义。本书后续将介绍这方面内容。
逐项积 (piecewise product),也叫 阿达玛乘积 (hadamard product)。两个相同形状向量的逐项积为对应位置元素分别相乘,结果为相同形状的向量。
逐项积的运算符为⊙。逐项积相当于算术乘法的批量运算。
举个例子,两个行向量逐项积如
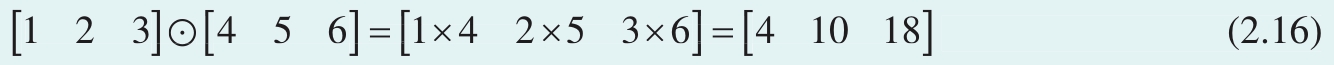
图2.6所示为向量逐项积运算示意图。

图2.6 向量逐项积
同理,两个矩阵逐项积的运算前提是——矩阵形状相同。矩阵逐项积运算规则为对应元素相乘,结果形状不变,如
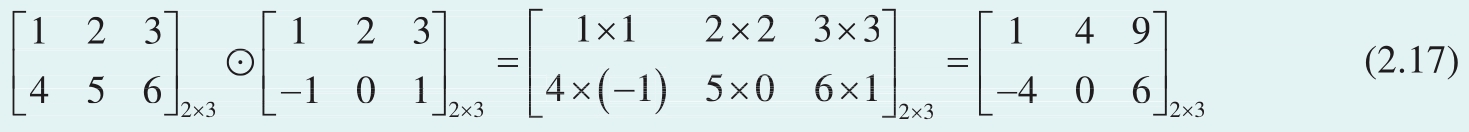
Python中,对于numpy.array()定义的形状相同的向量或矩阵,逐项积可以通过*计算得到。请大家参考Bk3_Ch2_08.py。更多有关NumPy用法,请参考《编程不难》。
矩阵乘法是最重要线性代数运算,没有之一——这句话并不夸张。
矩阵乘法规则可以视作算术“九九乘法表”的进阶版。
A 和 B 两个矩阵相乘的前提是矩阵 A 的列数和矩阵 B 的行数相同。 A 和 B 的乘积一般写作 AB 。
A 和 B 两个矩阵相乘 AB 读作“matrix boldface capital A times matrix boldface capital B ”或“the matrix product boldf ace capital A and boldface capital B ”。
NumPy中,两个矩阵相乘的运算符为@,鸢尾花书一部分矩阵乘法也会采用@。比如, AB 也记做 A @ B :
注意: A 在左边, B 在右边,不能随意改变顺序。也就是说,矩阵乘法一般情况下不满足交换律,即 AB ≠ BA 。

如图2.7所示,矩阵 A 的形状为 m 行、 p 列,矩阵 B 的形状为 p 行、 n 列。 A 和 B 相乘得到矩阵 C , C 的形状为 m 行、 n 列,相当于消去了 p 。

图2.7 矩阵乘法规则
再次强调,矩阵乘法不满足交换律。也就是说,一般情况下下式不成立,即

首先, B 的列数和 A 的行数很可能不匹配。即便 m = n ,也就是 B 的列数等于 A 的行数, BA 结果也很可能不等于 AB 。
下面,用两个2×2矩阵相乘讲解矩阵乘法运算规则。
设矩阵 A 和 B 相乘结果为矩阵 C ,有

图2.8所示为两个2×2矩阵相乘如何得到矩阵 C 的每一个元素。
矩阵 A 的第一行元素和矩阵 B 第一列对应元素分别相乘,再相加,结果为矩阵 C 的第一行、第一列元素 c 1,1 。
矩阵 A 的第一行元素和矩阵 B 第二列对应元素分别相乘,再相加,得到 c 1,2 。
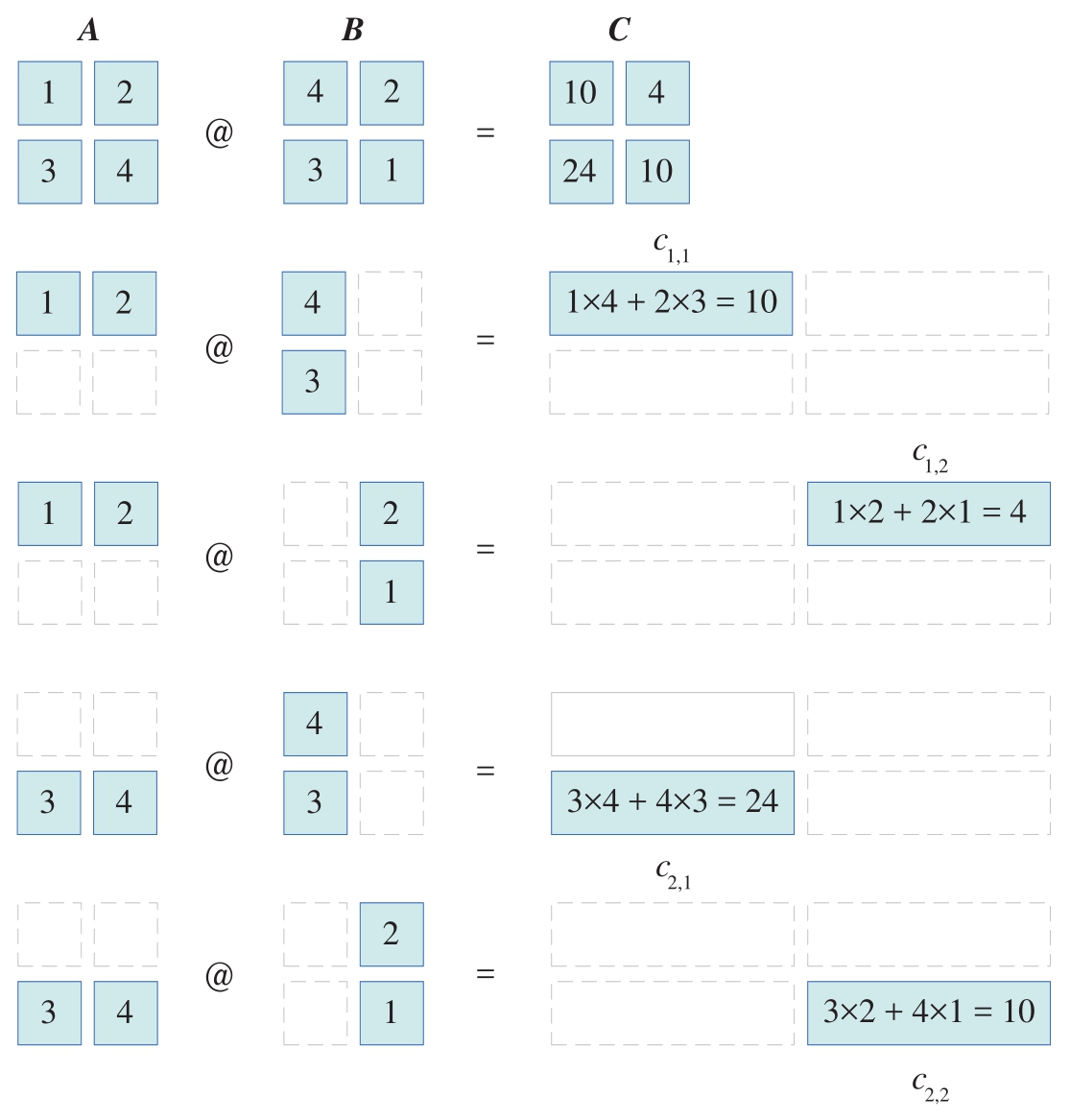
图2.8 矩阵乘法规则,两个2×2矩阵相乘为例
同理,依次获得矩阵 C 的 c 2,1 和 c 2,2 两个元素。
总结来说, A 和 B 乘积 C 的第 i 行第 j 列的元素 c i,j 等于矩阵 A 的第 i 行的元素与矩阵 B 的第 j 列对应元素乘积再求和。
注意:这个矩阵运算规则既是一种发明创造,也是一种约定成俗。也就是说,这种乘法规则在被法国数学家雅克·菲利普·玛丽·比内(Jacques Philippe Marie Binet, 1786—1856)提出之后,在长期的数学实践中被广为接受。矩阵乘法可谓“成人版九九乘法表”。就像大家儿时背诵九九乘法表时一样,这里建议大家先把矩阵乘法规则背下来,熟能生巧,慢慢地大家就会通过不断学习认识到这个乘法规则的精妙之处。
Bk3_Ch2_09.py展示如何完成矩阵乘法运算。
图2.9所示给出了常见的多种矩阵乘法形态,每一种形态对应一类线性代数问题。图2.9中特别高亮显示出矩阵乘法中左侧矩阵的“列”和右侧矩阵的“行”。高亮的“维度”在矩阵乘法中被“消去”。鸢尾花书《矩阵力量》一册将会详细介绍图2.9每一种乘法形态。
这里特别提醒大家,初学者对矩阵乘法会产生一种错误印象,认为这些千奇百怪的矩阵乘法形态就是“奇技淫巧”。这是极其错误的想法!在不断学习中,大家会逐渐领略到每种矩阵乘法形态的力量所在。
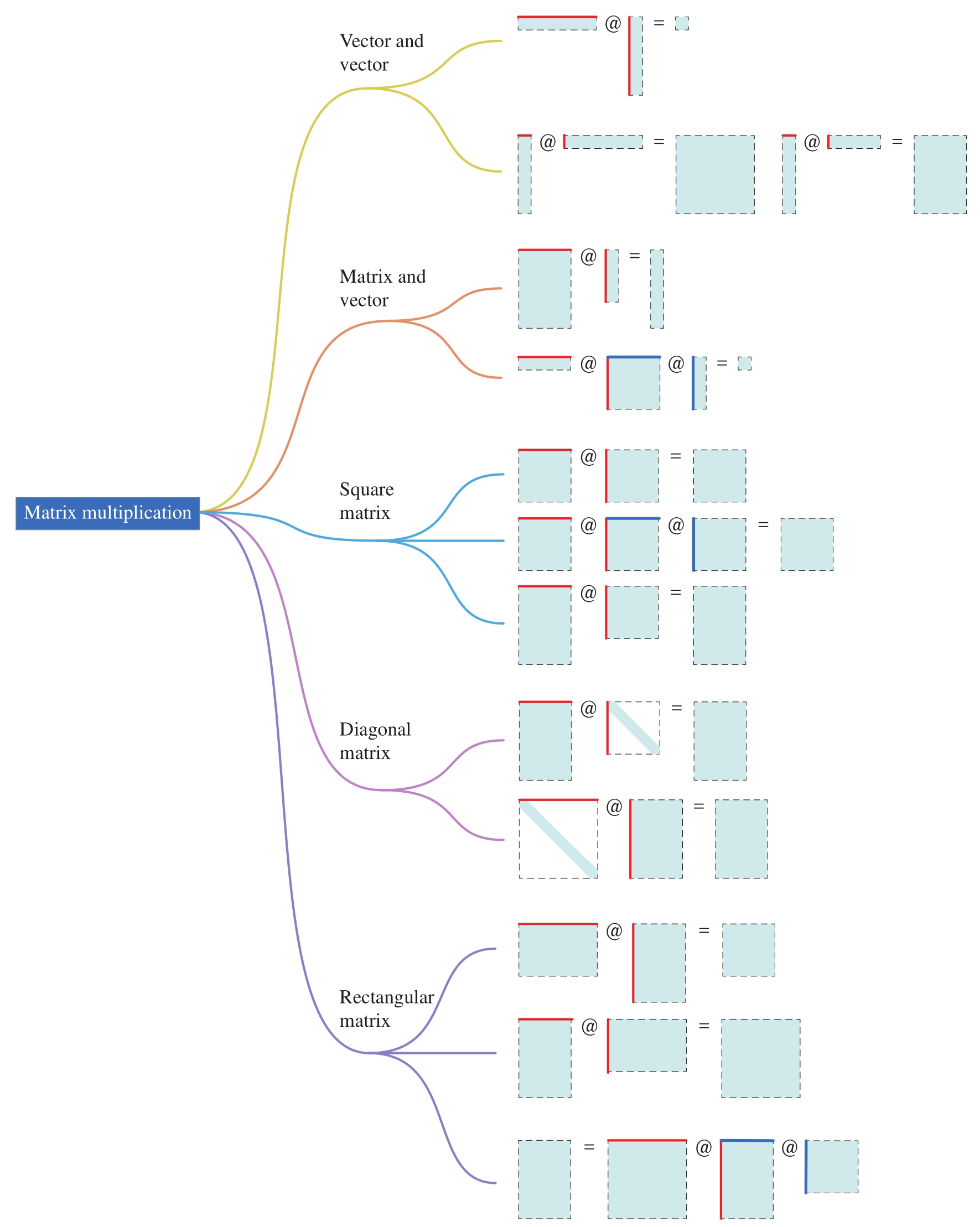
图2.9 矩阵乘法形态多样性
本节最后着重讲一下图2.9最上面两种向量的乘积。这两种特殊形态的矩阵乘法正是理解矩阵乘法规则的两个重要视角。
向量 a 和 b 为等长列向量, a 转置( a T )乘 b 为标量,等价于 a 和 b 的标量积,即

举个例子:

列向量 a 乘 b 转置( b T ),乘积结果 ab T 为方阵,也就是行数和列数相同的矩阵,即

如果 a 和 b 分别为不等长列向量,请大家自行计算 ab T 的结果:

再次强调:使用numpy.array()构造向量时,np.array([1,2])构造的是一维数组,不能算是矩阵。而np.array([[1,2]])构造得到的相当于1×2行向量,是一个特殊矩阵。注意,《编程不难》专门区分数组、向量、矩阵等概念。
np.array([[1],[2]])构造的是一个2×1列向量,也是个矩阵。鸢尾花书会在《矩阵力量》一册介绍更多构造行向量和列向量的方法。

这一节探讨矩阵乘法的第一视角。
上一节最后介绍, a 和 b 均是形状为 n ×1的列向量, a T b 结果为标量,相当于标量积 a · b 。我们可以把式(2.20)中 A 写成两个行向量 a (1) 和 a (2) ,把 B 写成两个列向量 b 1 和 b 2 ,即
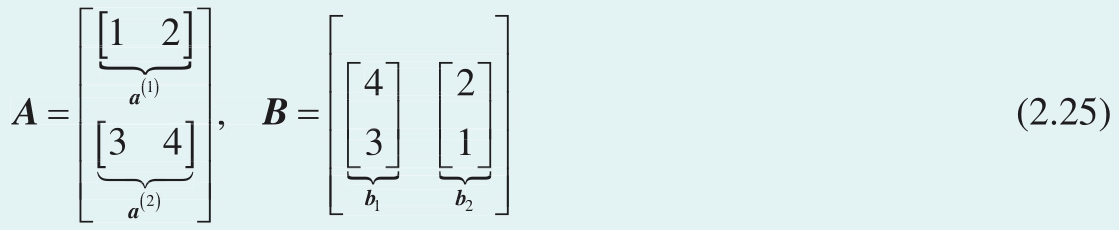
这样 AB 矩阵乘积可以写成

也就是说,将位于矩阵乘法左侧的 A 写成行向量,右侧的 B 写成列向量。然后,行向量和列向量逐步相乘,得到乘积每个位置的元素。
用符号代替具体数字,可以写成

式(2.27)展示的是矩阵乘法的基本视角,它直接体现出来的是矩阵乘法规则。
再次强调: a (1) 是行向量, b 1 是列向量。
矩阵乘积 AB 中,左侧矩阵 A 的形状为 m × p ,将矩阵 A 写成一组上下叠放的行向量 a ( i ) ,即

其中:行向量 a ( i ) 列数为 p ,即有 p 个元素。
矩阵乘积 AB 中,右侧矩阵 B 的形状为 p × n 列,将矩阵 B 写成左右排列的列向量,即

其中:列向量 b j 行数为 p ,也有 p 个元素。
A 和 B 相乘,可以展开写成

图2.10所示为 热图 (heatmap)可视化矩阵乘法。
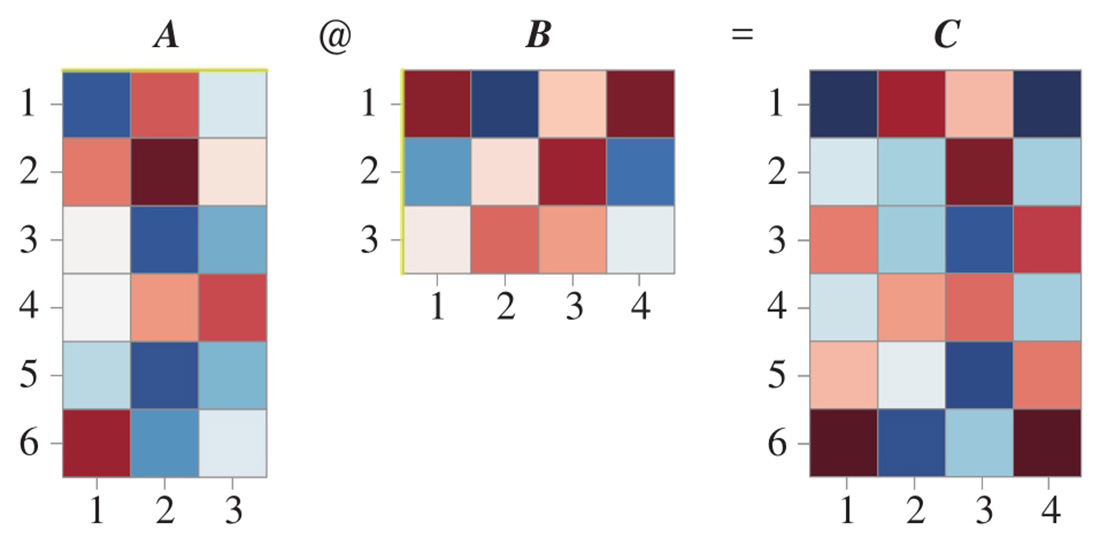
图2.10 矩阵乘法热图展示
具体如图2.11所示, A 中的第 i 行向量 a ( i ) 乘以 B 中的第 j 列向量 b j ,得到标量 a ( i ) b j ,对应乘积矩阵 C 中第 i 行、第 j 列元素 c i,j ,即

这就是矩阵乘法的第一视角。
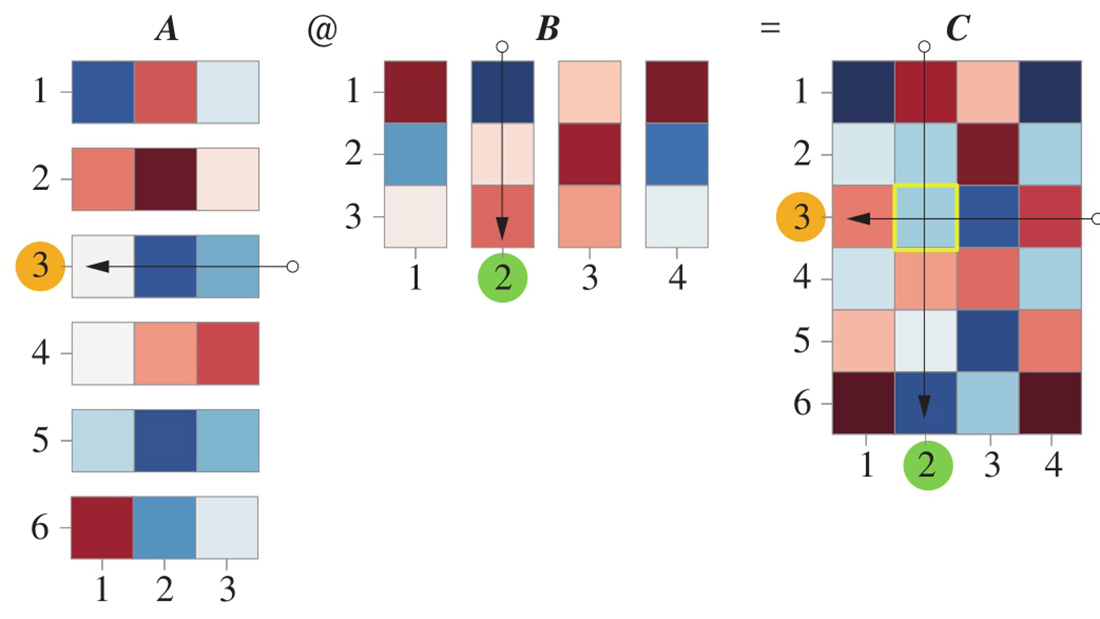
图2.11 矩阵乘法第一视角
代码文件Bk3_Ch2_10.py中Bk3_Ch2_10_A部分代码用于绘制图2.10。
代码用numpy.random.uniform()函数产生满足连续均匀分布的随机数,并用seaborn.heatmap()绘制热图。热图采用的colormap为'RdBu_r','Rd'是红色的意思,'Bu'是蓝色,'_r'代表“翻转”。
此外,我们还用Streamlit制作了展示矩阵乘法运算规则的App,请大家参考代码文件Streamlit_Bk3_Ch2_10.py。文件中还展示了如何使用try-except。
下面,我们聊一聊矩阵乘法的第二视角。
还是以式(2.20)为例, A 和 B 相乘,把左侧矩阵 A 写成两个列向量 a 1 和 a 2 ,把右侧矩阵 B 写成两个行向量 b (1) 和 b (2) ,即

这样 AB 乘积可以展开写成
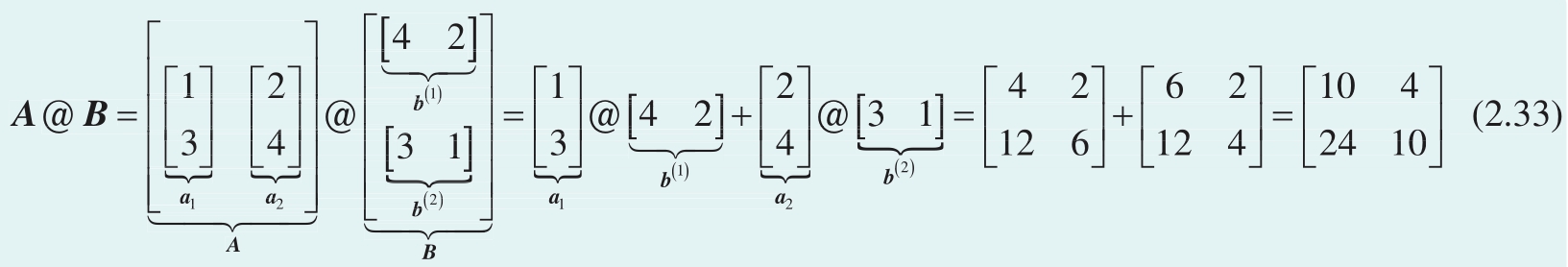
在这个视角下,我们惊奇地发现矩阵乘法竟然变成了“加法”!
用符号代替数字,可以写成
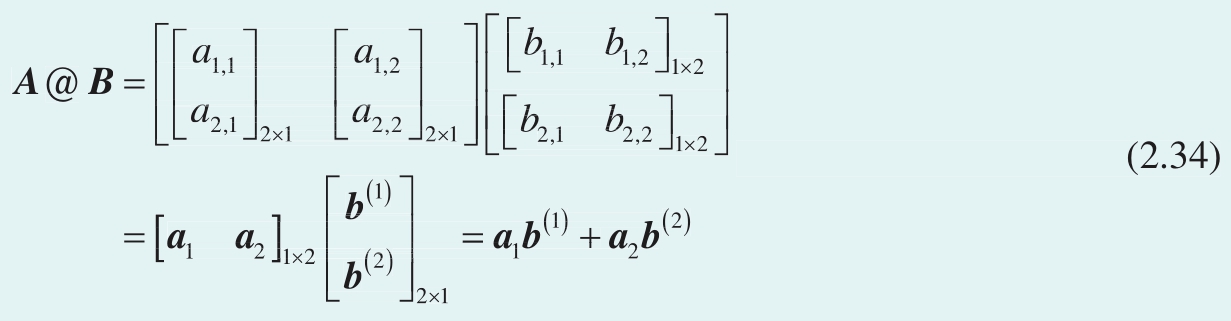
将矩阵 A m × p 写成一系列左右排列的列向量,即

其中:列向量 a i 元素数量为 m ,即行数为 m 。
将矩阵 B p × n 写成上下叠放的行向量,即

其中:行向量 b ( i ) 元素数量为 n ,即列数为 n 。
矩阵 A 和矩阵 B 相乘,可以展开写成 p 个 m × n 矩阵相加,即
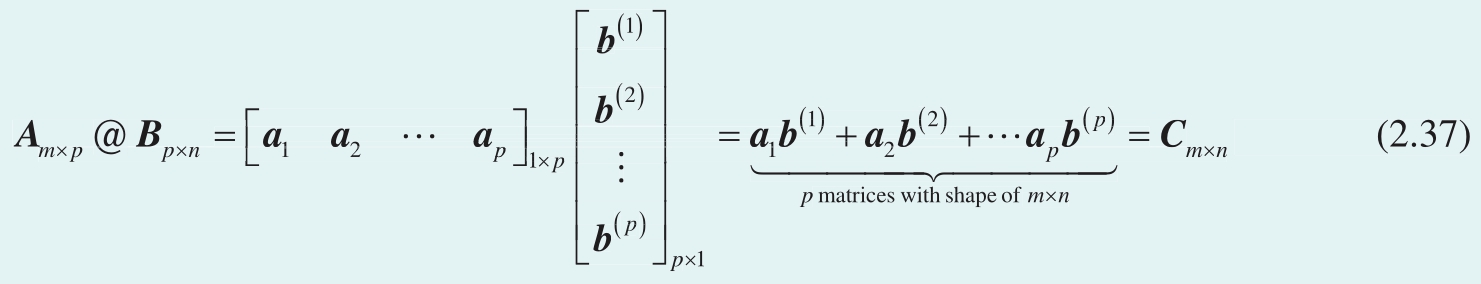
我们可以把 a k b ( k ) 的结果矩阵写成 C k ,这样 A 和 B 的乘积 C 可以写成 C k ( k =1, 2,…, p )之和,即

在这个视角下,矩阵的乘法变成了若干矩阵的叠加。这是一个非常重要的视角,数据科学和机器学习很多算法都离不开它。
图2.12所示给出的是图2.11所示矩阵乘法第二视角的热图。图2.12中三个形状相同矩阵 C 1 、 C 2 、 C 3 相加得到 C 。
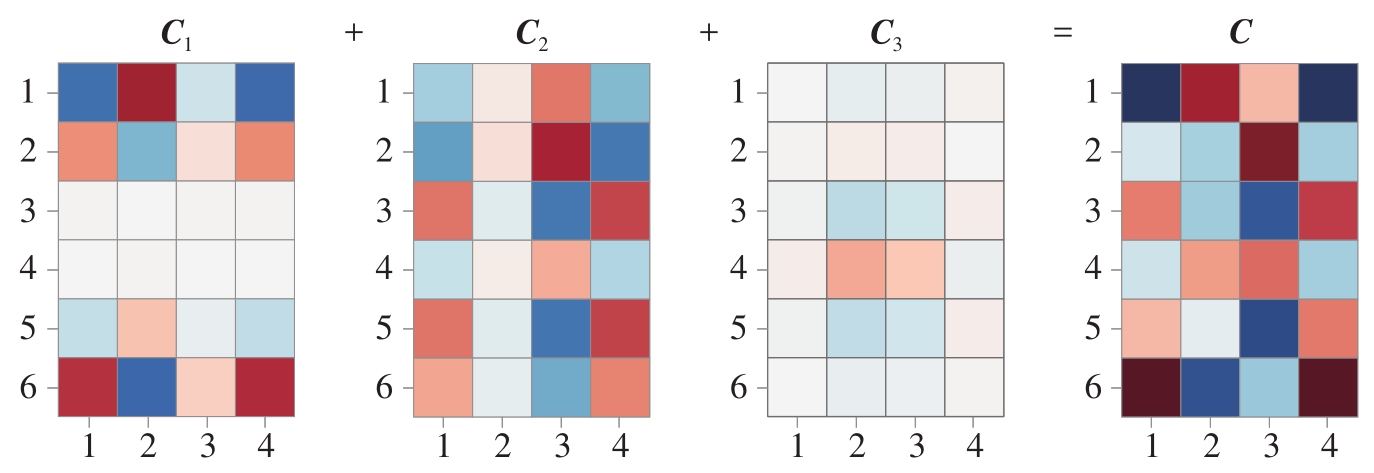
图2.12 矩阵乘法第二视角
如图2.13所示,从图像角度来看,好比若干形状相同的图片,经过层层叠加,最后获得了一幅完整的热图。式(2.38)中的 p 决定了参与叠加的矩阵层数。矩阵乘法中, p 所在维度被“消去”,这也相当于一种“压缩”。
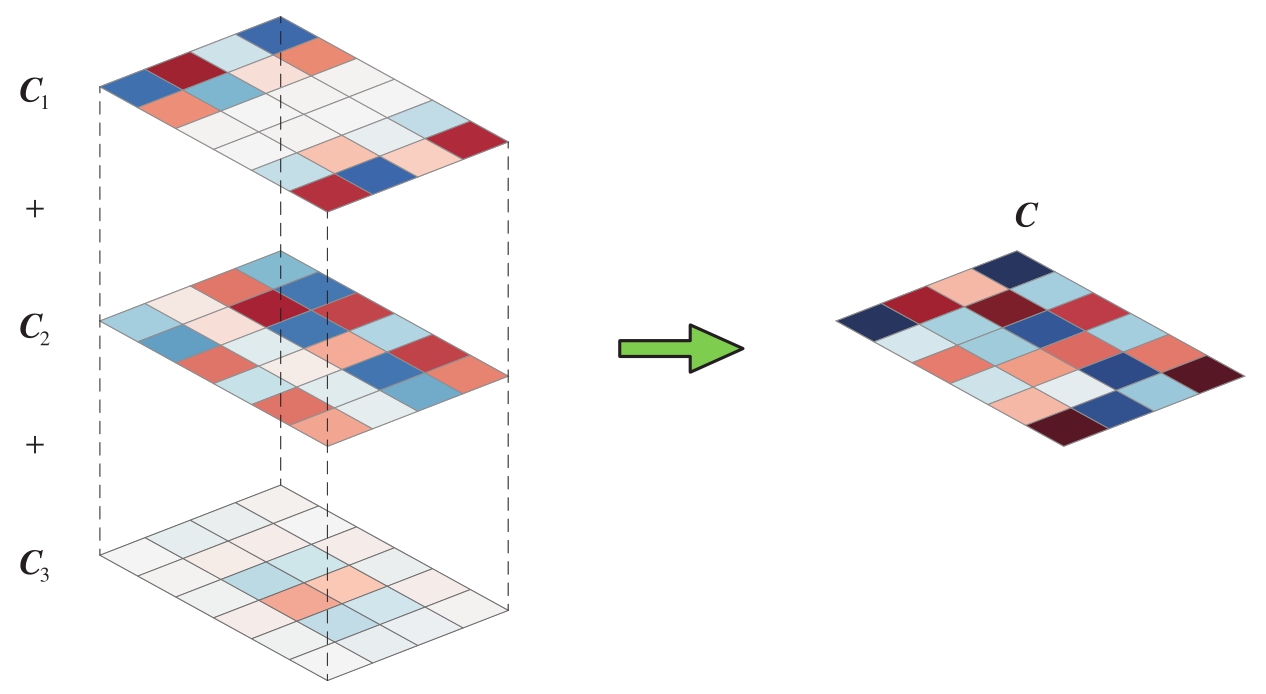
图2.13 三幅图像叠加得到矩阵 C 热图
图2.14、图2.15、图2.16所示分别展示了如何获得图2.12中矩阵 C 1 、 C 2 、 C 3 的热图。
鸢尾花书《矩阵力量》一册会讲解张量积。
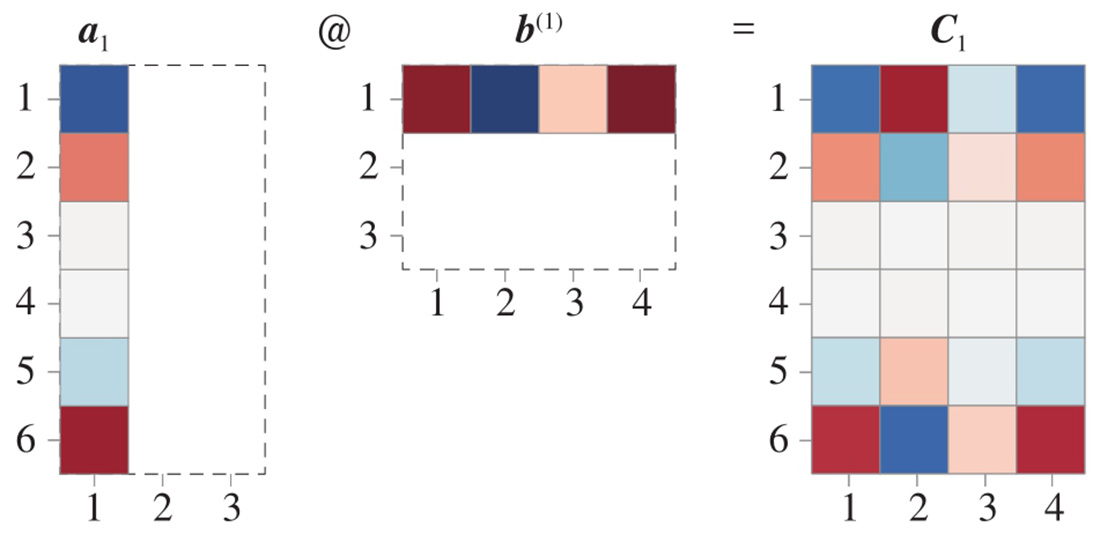
图2.14 获得 C 1
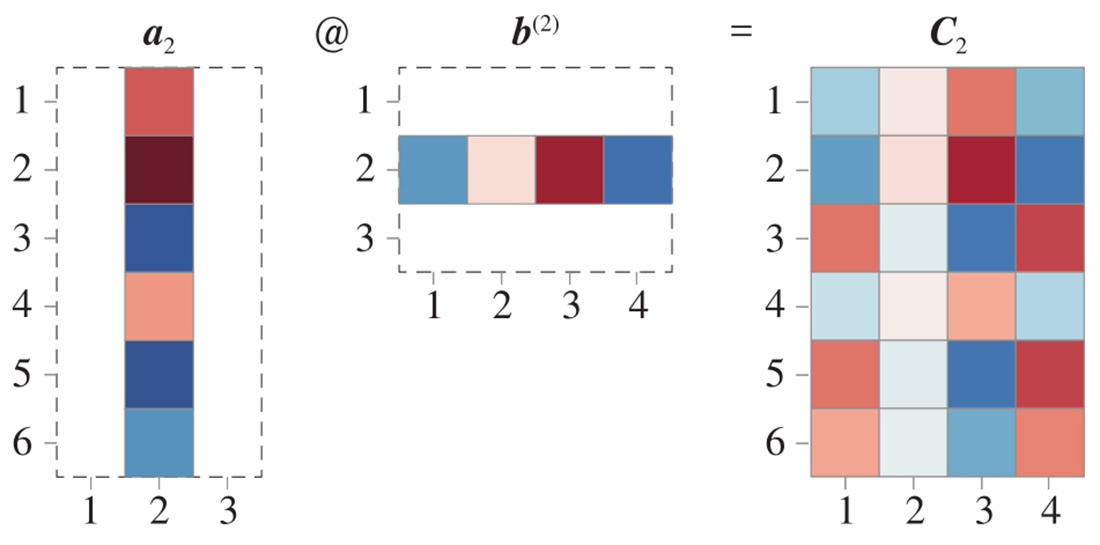
图2.15 获得 C 2
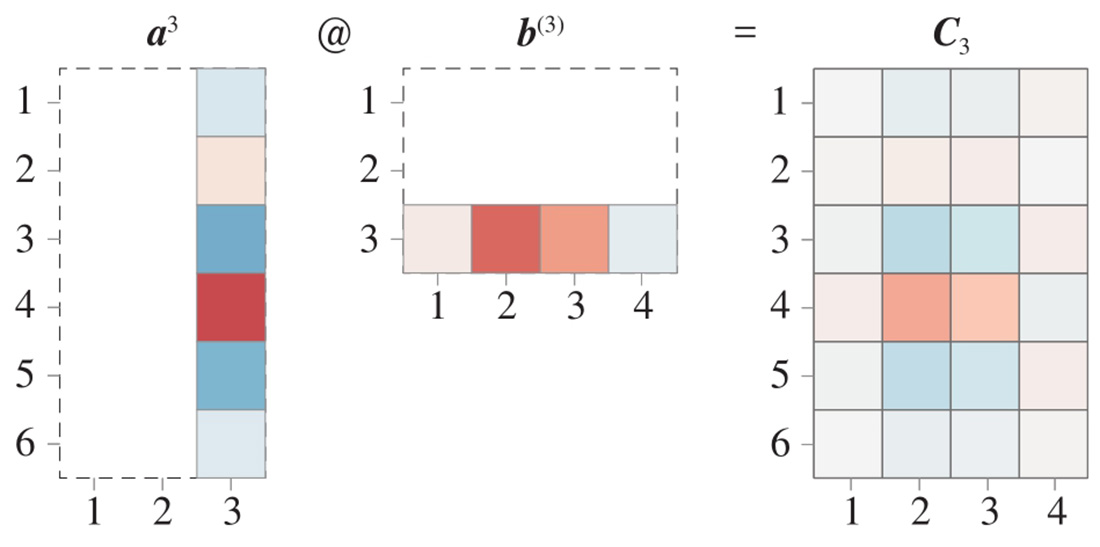
图2.16 获得 C 3
观察热图可以发现一个有意思的现象,列向量乘行向量好像张起了一幅平面。张量积用的就是类似于图2.14、图2.15、图2.16的运算思路。
代码文件Bk3_Ch2_10.py中Bk3_Ch2_10_B部分为绘制图2.12。
主成分分析 (Principal Component Analysis, PCA)是机器学习中重要的降维算法。这种算法可以把可能存在线性相关的数据转化成线性不相关的数据,并提取数据中的主要特征。
图2.17中, X 为原始数据, X 1 、 X 2 、 X 3 分别为第一、第二、第三主成分。根据热图颜色色差可以看出:第一主成分解释了原始数据中最大的差异;第二成分则进一步解释剩余数据中最大的差异,以此类推。
图2.17实际上就是本节介绍的矩阵乘法第二视角。鸢尾花书会在《矩阵力量》《统计至简》《数据有道》三本书中以不同视角介绍主成分分析。
《矩阵力量》将从矩阵分解、空间、优化等视角讲解PCA;《统计至简》将从数据、中心化数据、Z分数、协方差矩阵、相关性系数矩阵这些统计视角来讨论PCA不同技术路线之间的差异;《数据有道》则侧重讲解如何在实践中使用PCA分析数据,并使用PCA结果进行回归分析。
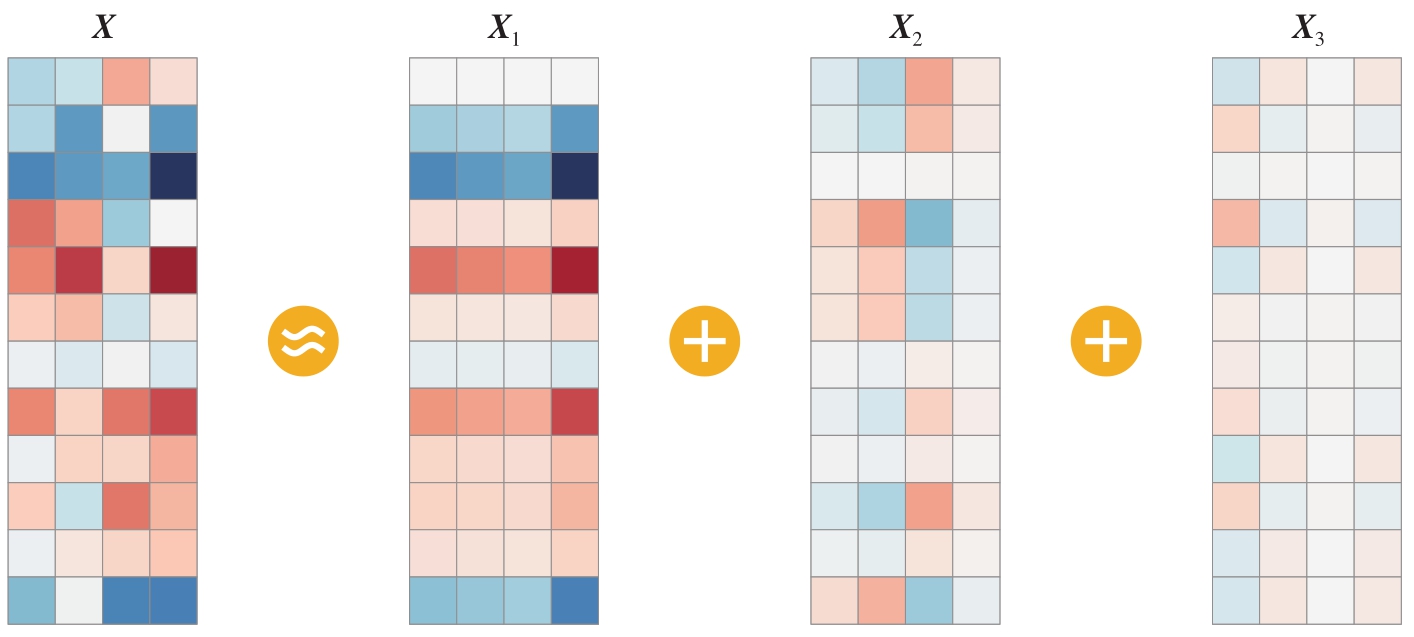
图2.17 用数据热图叠加看主成分分析
实际上,并不存在所谓的矩阵除法。所谓矩阵 B 除以矩阵 A ,实际上是将矩阵 A 先转化逆矩阵 A −1 ,然后计算 B 和逆矩阵 A −1 乘积,即

A 如果 可逆 (invertible),则仅当 A 为方阵且存在矩阵 A −1 使得下式成立

A −1 叫作 矩阵 A 的逆矩阵 (the inverse of matrix A )。
式(2.40)中的 I 就是前文介绍过的 单位矩阵 (identity matrix)。 n 阶单位矩阵 ( n -square identity matrix或 n -square unit matrix)的特点是对角线上的元素为1,其他为0,即

我们可以用numpy.linalg.inv()计算方阵的逆。
图2.18所示为方阵 A 和逆矩阵 A −1 相乘得到单位矩阵 I 的热图。
注意图中数值仅保留小数点后两位,按图中数值相乘不能准确得到单位矩阵。
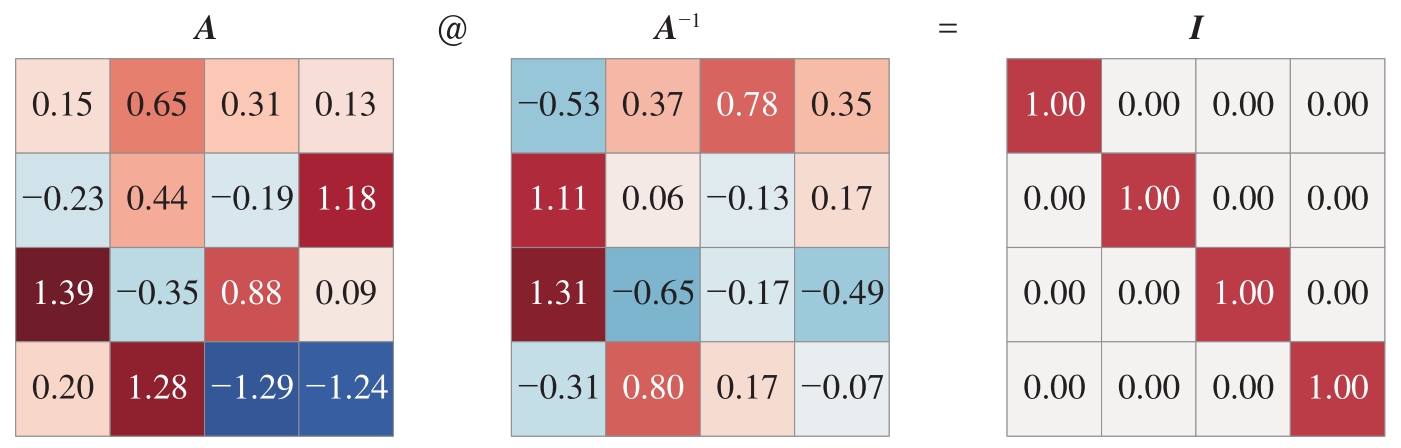
图2.18 方阵 A 和逆矩阵 A −1 相乘
一般情况,有

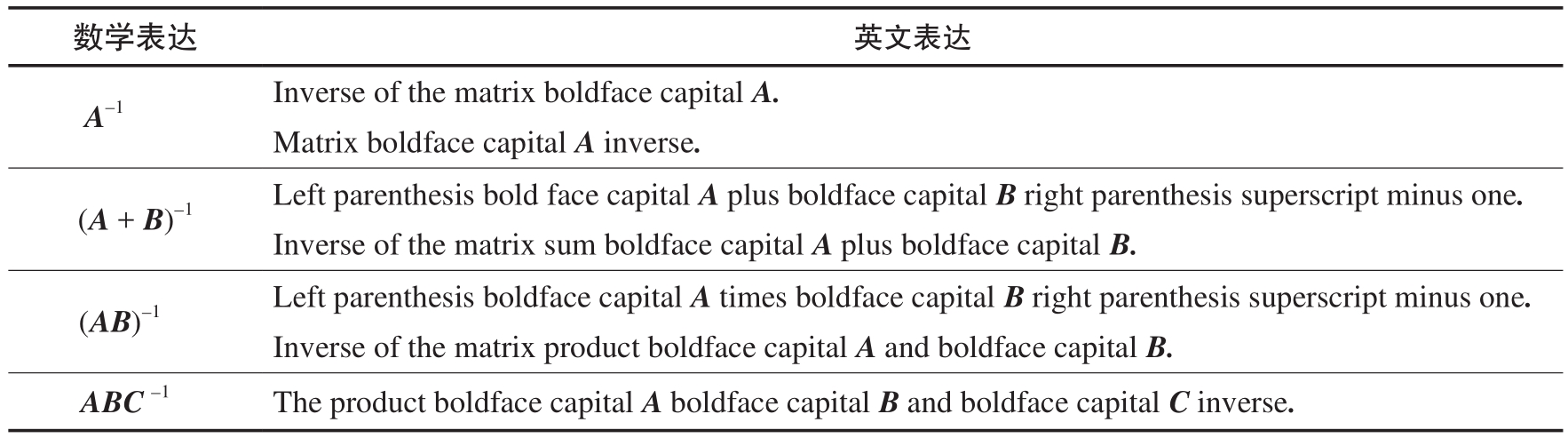
请大家注意以下和矩阵逆有关的运算规则:

其中:假设 A 、 B 、 C 、 AB 和 ABC 逆运算存在,且 k 不等于0。
表2.4总结常见矩阵逆相关的英文表达。
表2.4 和矩阵逆相关的英文表达
Bk3_Ch2_11.py计算并绘制图2.18。
如果学完这一章,大家对矩阵乘法规则还是一头雾水,我只有一个建议——死记硬背!
先别问为什么。就像背诵九九乘法口诀表一样,把矩阵乘法规则背下来。此外,再次强调矩阵乘法等运算不是“奇技淫巧”。后面,大家会逐步意识到矩阵乘法的洪荒伟力。