下载掌阅APP，畅读海量书库
立即打开
“万物皆数。
All is Number.
——毕达哥拉斯（Pythagoras）｜古希腊哲学家、数学家｜570 B.C.—495 B.C.”
◄ % 求余数 ◄ float() 将输入转化为浮点数 ◄ input() 函数接受一个标准输入数据，返回为string类型 ◄ int() 将输入转化为整数 ◄ is_integer() 判断是否为整数 ◄ lambda 构造匿名函数；匿名函数是指一类无须定义函数名的函数或子程序 ◄ len() 返回序列或者数据帧的数据数量 ◄ math.e math库中的欧拉数 ◄ math.pi math库中的圆周率 ◄ math.sqrt(2) math库中计算2的平方根 ◄ mpmath.e mpmath库中的欧拉数 ◄ mpmath.pi mpmath库中的圆周率 ◄ mpmath.sqrt(2) mpmath库中计算2的平方根 ◄ numpy.add() 向量或矩阵加法 ◄ numpy.array() 构造数组、向量或矩阵 ◄ numpy.cumsum() 计算累计求和 ◄ numpy.linspace() 在指定的间隔内,返回固定步长数组 ◄ numpy.matrix() 构造二维矩阵 ◄ print() 在console打印 ◄ range() 返回的是一个可迭代对象，range(10)返回0 ~ 9，等价于range(0, 10)；range(1, 11)返回 1 ~ 10；range(0, -10, -1) 返回 0 ~ -9；range(0, 10, 3) 返回 [0, 3, 6, 9]，步长为3 ◄ zip(*) 将可迭代的对象作为参数，让对象中对应的元素打包成一个个元组，然后返回由这些元组组成的列表。 *代表解包，返回的每一个都是元组类型，而并非是原来的数据类型
数字，就是人类思想的空气，无处不在，不可或缺。
大家不妨停止阅读，用一分钟时间，看看自己身边哪里存在数字。
举目四望，你会发现，键盘上有数字，书本上印着数字，手机上显示数字，交易媒介充满了数字，食品有卡路里数值，时钟上的数字提醒我们时间，购物扫码本质上也是数字。一串串手机号码让人们联通，身份编号是我们的个体标签……
当下，数字已经融合到人类生活的方方面面。多数时候，数字像是空气，我们认为它理所应当，甚至忽略了它的存在。
数字是万物的绝对尺度，数字更是一种高阶的思维方式。远古时期，不同地域、不同族群的人类突然意识到，2只鸡、2只兔、2头猪，有一个共性，那就是——2。
2和更多数字，以及它们之间的加、减、乘、除和更多复杂运算被抽象出来，这是人类思想的一次伟大飞跃，如图1.1所示。
数字这一宝贵的人类遗产，在不同地区、不同种族之间薪火相传。
5000年前，古巴比伦人将各种数学计算，如倒数、平方、立方等刻在泥板上，如图1.2所示。古埃及则是将大量数学知识记录在纸草上。
图1.1 数字是人类抽象思维活动的产物
图1.2 古巴比伦泥板（图片来自Wikipedia）
古巴比伦采用六十进制。不谋而合的是，中国自古便发明了使用天干地支六十甲子为一个周期来纪年。
今人所说的“阿拉伯数字”实际上是古印度人创造的。古印度发明了 十进制 （decimal system），而古阿拉伯人将它们发扬光大。中世纪末期，十进制传入欧洲，而后成为全世界的标准。中国古代也创造了十进制。
有学者认为，人类不约而同地发明并广泛使用十进制，是因为人类有十根手指。人们数数的时候，自然而然地用手指记录。
虽然十进制大行其道，但是其他进制依然广泛运用。比如， 二进制 （binary system）、 八进制 （octal system）和 十六进制 （hexadecimal system）经常在电子系统中使用。
日常生活中，我们不知不觉中也经常使用其他进制。 十二进制 （duodecimal system）常常出现，比如十二小时制、一年十二个月、 黄道十二宫 （zodiac）、 十二地支 （Earthly Branches）、 十二生肖 （Chinese zodiac）。四进制也不罕见，如一年四个季度。二十四进制用在一天24小时、一年二十四节气。六十进制也很常用，如一分钟60秒、一小时60分钟。
随着科学技术持续发展，人类的计算也日趋复杂。零、负数、分数、小数、无理数、虚数被发明创造出来。与此同时，人类也在发明改进计算工具，让计算更快、更准。
算盘，作为一种原始的计算工具，现在已经基本绝迹。随着运算量和复杂度的不断提高，人们对运算速度、准确度的需求激增，人类亟需摆脱手工运算，计算器应运而生。
1622年，英国数学家 威廉·奥特雷德 （William Oughtred）发明了计算尺。早期计算尺主要用于四则运算，而后发展到可以用于求对数和三角函数。直到二十世纪后期被便携式计算器代替之前，计算尺一度是科学和工程重要的计算工具。
1642年，法国数学家 帕斯卡 （Blaise Pascal）发明了机械计算器，这台机器可以直接进行加减运算，如图1.3所示。难以想象，帕斯卡设计自己第一台计算器时未满19岁。
图1.3 帕斯卡机械计算器和原理图纸（图片来自Wikipedia）
1822年前后，英国数学家 查尔斯·巴贝奇 （Charles Babbage），设计完成了 差分机 （Difference Engine）。第一台差分机重达4吨，最高可以存16位数。差分机是以蒸汽机为动力的自动机械计算器，它已经很接近世界第一台计算机。因此，也有很多人将查尔斯·巴贝奇称为“计算器之父”。
1945年，ENIAC诞生。ENIAC的全称为 电子数值积分计算机 （Electronic Numerical Integrator And Computer）。ENIAC是一台真正意义上的电子计算机。ENIAC重达27吨，占地167平方米，如图1.4所示。
图1.4 ENIAC计算机（图片来自Wikipedia）
20世纪50年代电子计算机主要使用真空管制作，而后开始使用半导体晶体管制作。半导体使得计算机体积变得更小、成本更低、耗电更少、性能更可靠。进入20世纪，计算机器的更新迭代，让人目不暇接，甚至让人感觉窒息。
20世纪70年代，集成电路和微处理器先后投入大规模使用，计算机和其他智能设备开始逐渐步入寻常百姓家。现如今，计算的竞赛愈演愈烈，量子计算机的研究进展如火如荼，如图1.5所示。
图1.5 计算器发展历史时间轴
到这里，不妨停下来，喘口气，回望来时的路。再去看看数字最朴素、最原始、最直觉的形态。
本节介绍数字分类，介绍的数字类型如图1.6所示。
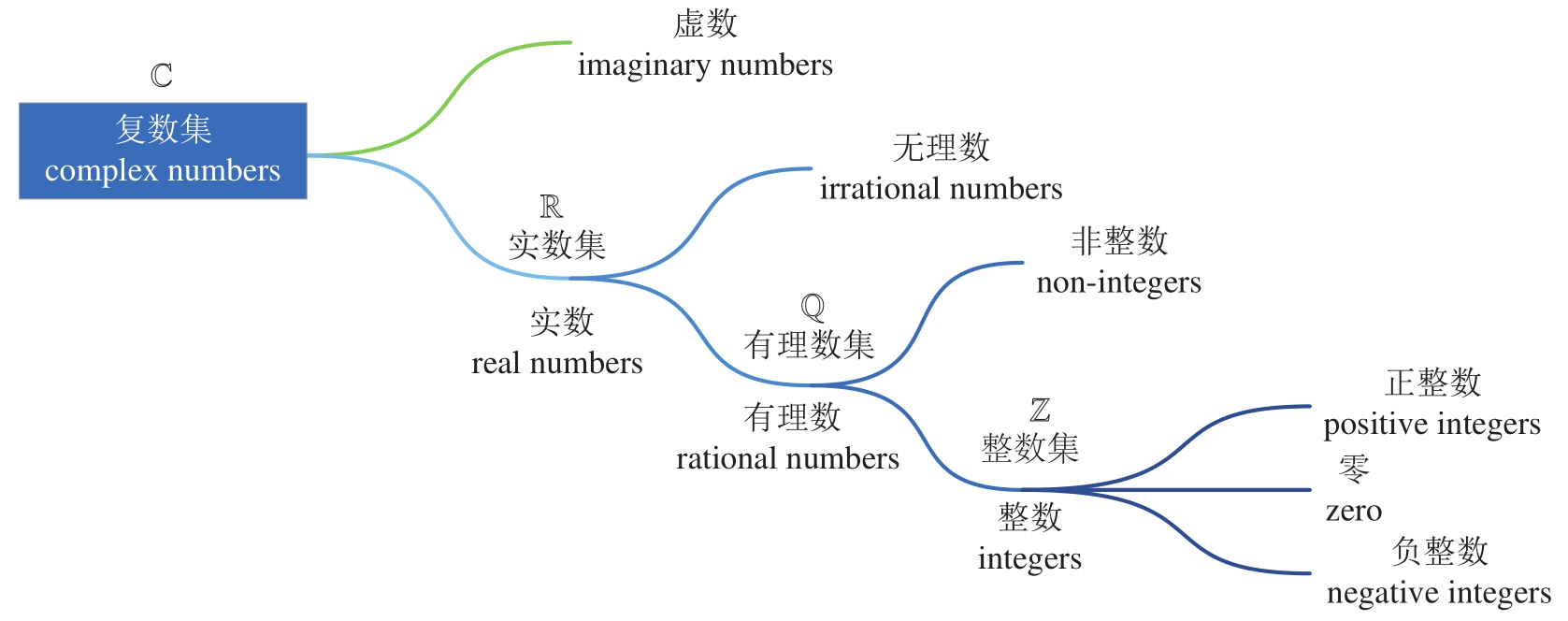
图1.6 数字分类
复数
（complex number）包括
实数
（real numbers）和
虚数
（imaginary number）。
复数集
（the set of complex numbers）的记号为
。
集合 （set），简称 集 ，是指具有某种特定性质 元素 （element）的总体。通俗地讲，集合就是一堆东西构成的整体。因此，复数集是所有复数构成的总体。
复数的具体形式为
其中： a 和 b 是实数。
式（1.1）中，i是 虚数单位 （imaginary unit），i的平方等于-1，即
笛卡儿 （René Descartes）最先提出虚数这个概念。而后， 欧拉 （Leonhard Euler）和 高斯 （Carl Friedrich Gauss）等人对虚数做了深入研究。注意，根据ISO标准叙述单位i为正体，即非斜体。
有意思的是，不经意间，式（1.1）中便使用 a 和 b 来代表实数。用抽象字母来代表具体数值是代数的基础。 代数 （algebra）的研究对象不仅是数字，还包括各种抽象化的结构。
实数集
（the set of real numbers）记号为
。实数包括
有理数
（rational numbers）和
无理数
（irrational numbers）。
式（1.1）中， b =0时，得到的便是实数。如图1.7所示，实数集合可以用 实数轴 （real number line或real line）来展示。
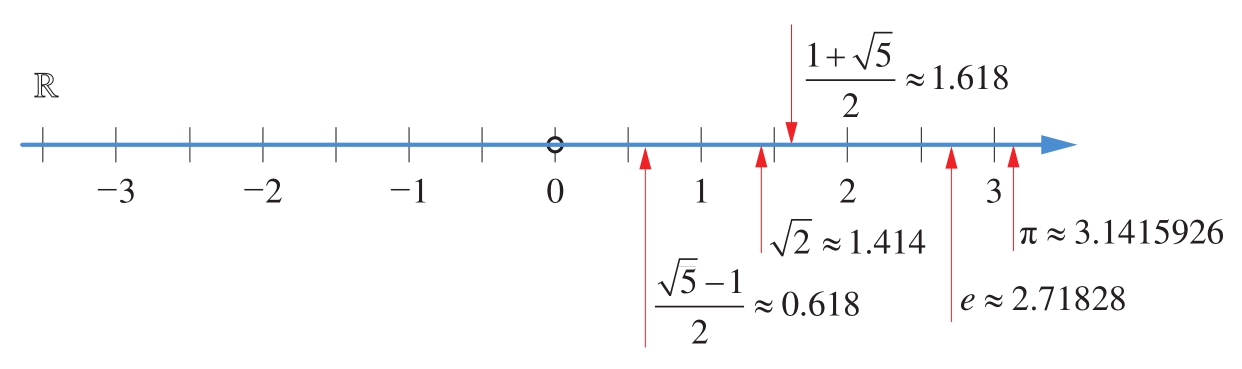
图1.7 实数轴
数轴和坐标系的发明让代数和几何前所未有地结合在了一起，这是本书第5、6章要介绍的内容。
无意之间，我们又用到了解析几何中重要的工具之一—— 数轴 （number line）。图1.7这看似平凡无奇的一根数轴，实际上是人类的一个伟大发明创造。
数轴描述一维空间，两根垂直并相交于原点的数轴可以张成二维直角坐标系，即 笛卡儿坐标系 （Cartesian coordinate system）。在二维直角坐标系原点处升起一根垂直于平面的数轴，便张成了三维直角坐标系。
目前，数学被分割成一个个板块——算数、代数、几何、解析几何、线性代数、概率统计等。这种安排虽然有利于特定类别的数学工具学习，但是板块之间的联系被人为割裂。本书的重要任务之一就是强化各个板块之间的联系，让大家看见“森林”，而不是一棵棵“树”。
有理数集合用
表示，有理数可以表达为
两个整数的商
（quotient of two integers），形如
其中： a 为 分子 （numerator）； b 为 分母 （denominator）。式（1.3）中 分母不为零 （The denominator is not equal to zero）。
有理数可以表达为 有限小数 （finite decimal或terminating decimal）或者 无限循环小数 （repeating decimal或recurring decimal）。小数中的圆点叫作 小数点 （decimal separator）。
图1.7所示的实数轴上除有理数以外，都是无理数。无理数不能用一个整数或两个整数的商来表示。无理数也叫 无限不循环小数 （non-repeating decimal）。
很多重要的数值都是无理数，如图1.7所示数轴上的圆周率π（pi）、
（the square root of two）、
自然常数
e（exponential constant）和
黄金分割比
（golden ratio）等。自然常数e也叫
欧拉数
（Euler’s number）。
执行Bk3_Ch1_01.py代码，可以打印出π、e和
的精确值。代码使用了math库中函数，math库是Python提供的内置数学函数库。
打印结果如下：
pi = 3.141592653589793
e = 2.718281828459045
sqrt(2) = 1.4142135623730951
下面，我们做一个有趣的实验——打印圆周率和自然常数e小数点后1,000位数字。图1.8所示为圆周率小数点后1,000位，图1.9所示采用热图的形式展示圆周率小数点后1,024位。图1.10所示为自然常数e小数点后1,000位。
中国古代南北朝时期数学家 祖冲之 （429—500）曾刷新圆周率估算纪录。他估算圆周率在3.1415926到3.1415927之间，这一记录在之后的约1,000年内无人撼动。圆周率的估算是本书的一条重要线索，我们将追随前人足迹，用不同的数学工具估算圆周率。
图1.8 圆周率小数点后1,000位
图1.9 圆周率小数点后1,024位热图
图1.10 自然常数e小数点后1,000位
Bk3_Ch1_02.py打印圆周率、
和自然常数e，小数点后1,000位数字。mpmath是一个任意精度浮点运算库。
目前，背诵pi小数点后最多位数的吉尼斯世界纪录是70,000位。该纪录由印度人在2015年创造，用时近10小时。这一纪录需要背诵的数字量是图1.8所示的70倍，感兴趣的读者可以修改代码获取，并打印保存这些数字。计算取决于个人计算机的算力，这一过程可能要用时很久。
观察图1.8所示的圆周率小数点后1,000位数字，可以发现0~9这十个数字反复随机出现。这里，“随机（random）”是指偶然、随意、无法预测，《统计至简》将会大量使用“随机”这个概念。
大家能否凭直觉猜一下哪个数字出现的次数最多？圆周率小数点后10,000位、100,000位，乃至1,000,000位，0~9这十个数字出现的次数又会怎样？
答案就在Streamlit_Bk3_Ch1_02.py文件中。我们用Streamlit创作了一个数学动画App展示圆周率小数点后0~9这十个数出现的次数。
整数
（integers）包括
正整数
（positive integers）、
负整数
（negative integers）和零（zero）。正整数
大于零
（greater than zero）；负整数
小于零
（less than zero）。整数集用
表示。
整数的重要性质之一是——整数相加、相减或相乘的结果还是整数。
奇偶性 （parity）是整数另外一个重要性质。 能被2整除的整数称为偶数 （an integer is called an even integer if it is divisible by two）；否则， 该整数为奇数 （the integer is odd）。
利用以上原理，我们可以写一段Python代码，判断数字奇偶性。请大家参考Bk3_Ch1_03.py。代码中，%用于求余数。
自然数 （natural number或counting number）有时指的是正整数，有时指的是 非负整数 （nonnegative integer），这时自然数集合包括“0”。“0”是否属于自然数尚未达成一致意见。
至此，我们回顾了常见数字类型。表1.1中总结了数字类型并给出了例子。
表1.1 不同种类数字及举例
本节介绍加、减这两种最基本算数运算。
加法 （addition）的运算符为 加号 （plus sign或plus symbol）；加法运算式中， 等式 （equation）的左边为 加数 （addend）和 被加数 （augend或summand），等式的右边是 和 （sum），如图1.11所示。
加法的表达方式多种多样，如“ 和 （summation）”“ 加 （plus）”“ 增长 （increase）”“ 小计 （subtotal）”和“ 总数 （total）”等。
图1.11 加法运算
图1.12所示是在数轴上可视化2+3=5这一加法运算。
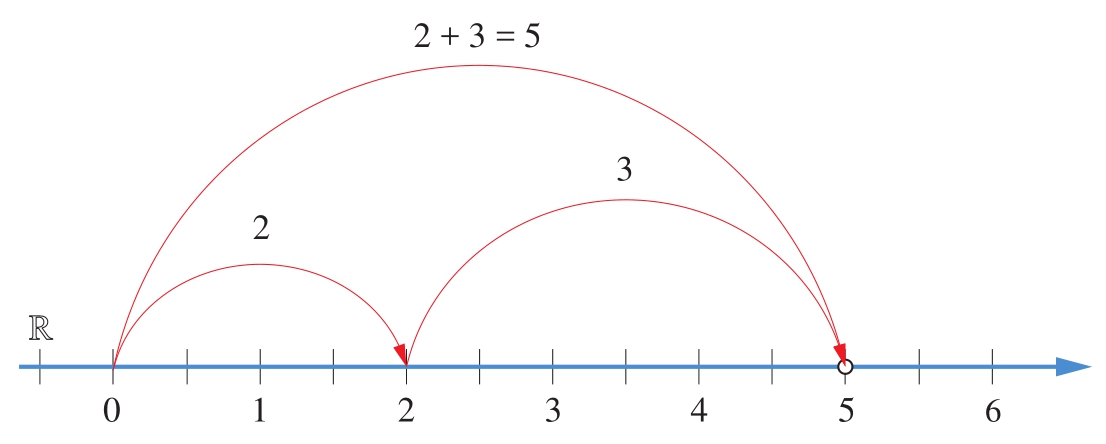
图1.12 2+3=5在数轴上的可视化
Bk3_Ch1_04.py完成图1.12所示加法运算。
Bk3_Ch1_05.py对Bk3_Ch1_04.py稍作调整，利用input（）函数，让用户通过键盘输入数值。
结果打印如下：
Enter first number: 2
Enter second number: 3
The sum of 2 and 3 is 5.0
表1.2总结了加法的常用英文表达。
表1.2 加法的英文表达
对于一行数字， 累计求和 （cumulative sum或cumulative total）得到的结果不是一个总和，而是从左向右每加一个数值，得到的分步结果。比如，自然数1到10累计求和的结果为
式（1.4）累计求和计算过程为
Bk3_Ch1_06.py利用numpy.linspace（1, 10, 10）产生1~10这十个自然数，然后利用numpy.cumsum（）函数进行累计求和。NumPy是一个开源的Python库，鸢尾花书的大量线性代数运算都离不开NumPy。
减法 （subtraction）是 加法的逆运算 （inverse operation of addition），运算符为 减号 （minus sign）。如图1.13所示，减法运算过程是， 被减数 （minuend）减去 减数 （subtrahend）得到 差 （difference）。
减法的其他表达方式包括“ 减 （minus）”“ 少 （less）”“ 差 （difference）”“ 减少 （decrease）”“ 拿走 （take away）”和“ 扣除 （deduct）”等。
图1.13 减法运算
图1.14所示为在数轴上展示5–3=2的减法运算。
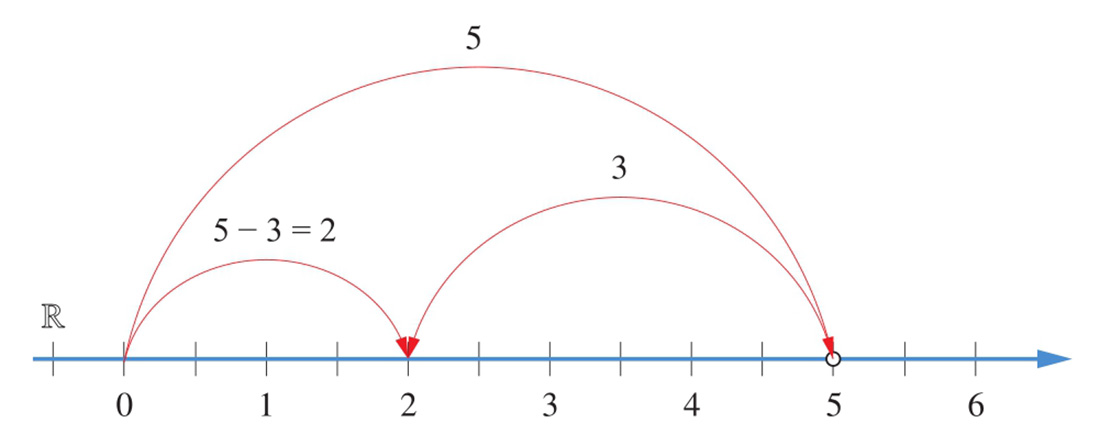
图1.14 5–3=2在数轴上的可视化
Bk3_Ch1_07.py完成图1.14所示的减法运算。
求 相反数 （inverse number或additive inverse number）的过程是 改变符号 （reverses its sign），这样的操作常称做 变号 （sign change）。比如，5的相反数为-5（negative five）。表1.3给出了减法常用的英文表达。
表1.3 减法常见英文表达
到了本节读者会问，明明第一章讲的是算数，怎么一下扯到了“向量”这个线性代数的概念呢？
向量、矩阵等线性代数概念对于数据科学和机器学习至关重要。在机器学习中，数据几乎都以矩阵形式存储、运算。毫不夸张地说，没有线性代数就没有现代计算机运算。逐渐地，大家会发现算数、代数、解析几何、微积分、概率统计、优化方法并不是一个个孤岛，而线性代数正是连接它们的重要桥梁之一。
然而，部分初学者对向量、矩阵等概念却表现出了特别抗拒，甚至恐惧的态度。
基于以上考虑，本书把线性代数基础概念穿插到各个板块，以便突破大家对线性代数的恐惧，加强大家对这个数学工具的理解。
下面书归正传。
若干数字排成一行或一列，并且用中括号括起来，得到的数组叫作 向量 （vector）。
排成一行的叫作 行向量 （row vector），排成一列的叫作 列向量 （column vector）。
通俗地讲，行向量就是表格的一行数字，列向量就是表格的一列数字。以下两例分别展示了行向量和列向量，即
注意：用numpy.array（）函数定义向量（数组）时如果只用一层中括号[]，比如numpy.array（[1, 2, 3]），得到的结果只有一个维度；有两层中括号[[ ]]，numpy.array（[[1, 2, 3]]）得到的结果有两个维度。这一点在NumPy库矩阵运算中非常重要。
式（1.6）中，下角标“1×3”代表“1行、3列”，“3×1”代表“3行、1列”。本书在给出向量和矩阵时，偶尔会以下角标形式展示其形状，如 X 150 × 4 代表矩阵 X 有150行、4列。
利用NumPy库，可以用numpy.array（[[1, 2, 3]]）定义式（1.6）中的行向量。用numpy.array（[[1], [2], [3]]）定义式（1.6）中的列向量。
鸢尾花书采用的转置符号为上标“T”。行向量 转置 （transpose）可得到列向量；同理，列向量转置可得到行向量。举例如下，有
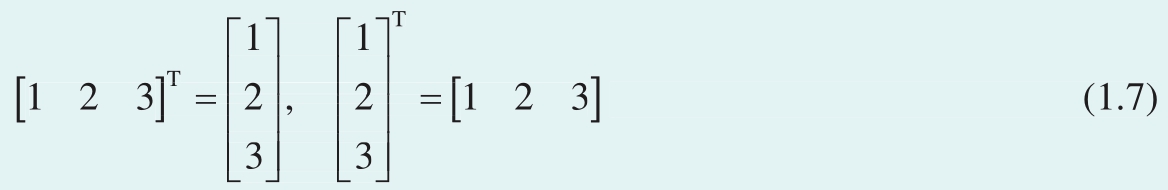
如图1.15所示，转置相当于镜像。图1.15中的红线就是镜像轴，红线从第1行、第1列元素出发，朝向右下方45°。
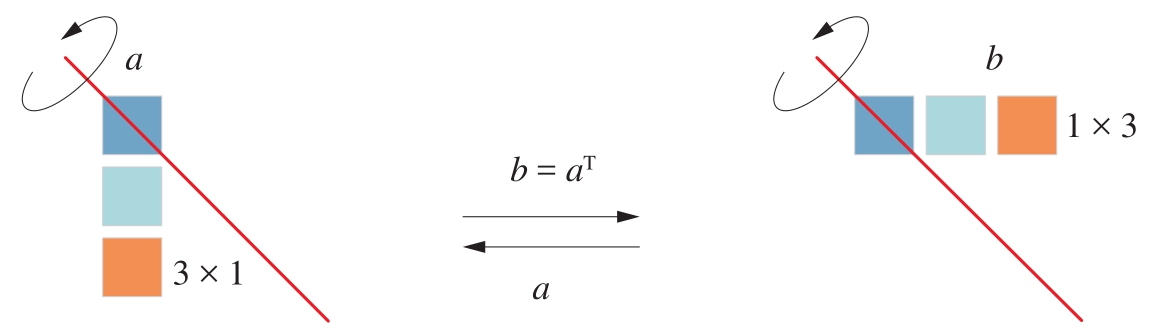
图1.15 向量转置
鸢尾花书用加粗、斜体小写字母来代表向量，如图1.15中的向量 a 和向量 b 。
给定如下行向量 a ， a 有 n 个元素，元素本身用小写字母表示，如
其中：下角标代表向量元素的序数。[ a 1 , a 2 ,… a n ]读作“ n row vector, a sub one, a sub two, dot dot dot, a sub n ”。
Bk3_Ch1_08.py定义行向量和列向量，并展示如何通过转置将行向量和列向量相互转换。
本书在介绍线性代数相关知识时，会尽量使用具体数字，而不是变量符号。这样做的考虑是，让读者构建向量和矩阵运算最直观的体验。这给鸢尾花书《矩阵力量》一册打下基础。
《矩阵力量》一册则系统讲解线性代数知识，以及线性代数与代数、解析几何、微积分、概率统计、优化方法、数据科学等板块的联系。
矩阵 （matrix）将一系列数字以长方形方式排列，如
通俗地讲，矩阵将数字排列成表格，有行、有列。式（1.9）给出了三个矩阵，形状分别是2行3列（记作2×3）、3行2列（记作3×2）和2行2列（记作2×2）。
鸢尾花书用大写、斜体字母代表矩阵，比如矩阵 A 和矩阵 B 。
图1.16所示为一个 n × D （ n by capital D ）矩阵 X ， n 是 矩阵的行数 （number of rows in the matrix）， D 是 矩阵的列数 （number of columns in the matrix）。 X 可以展开写成表格形式，即
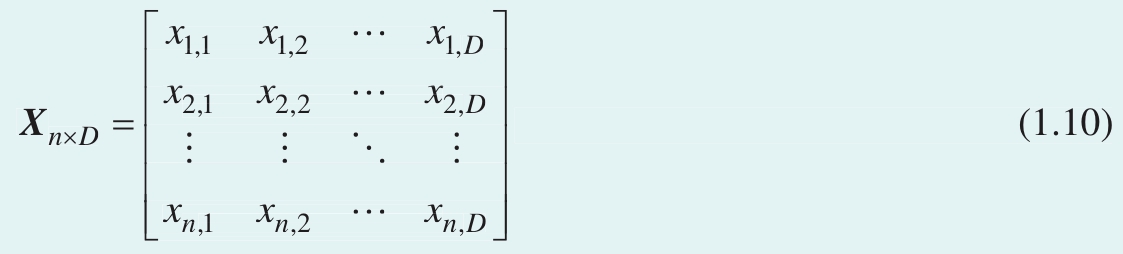
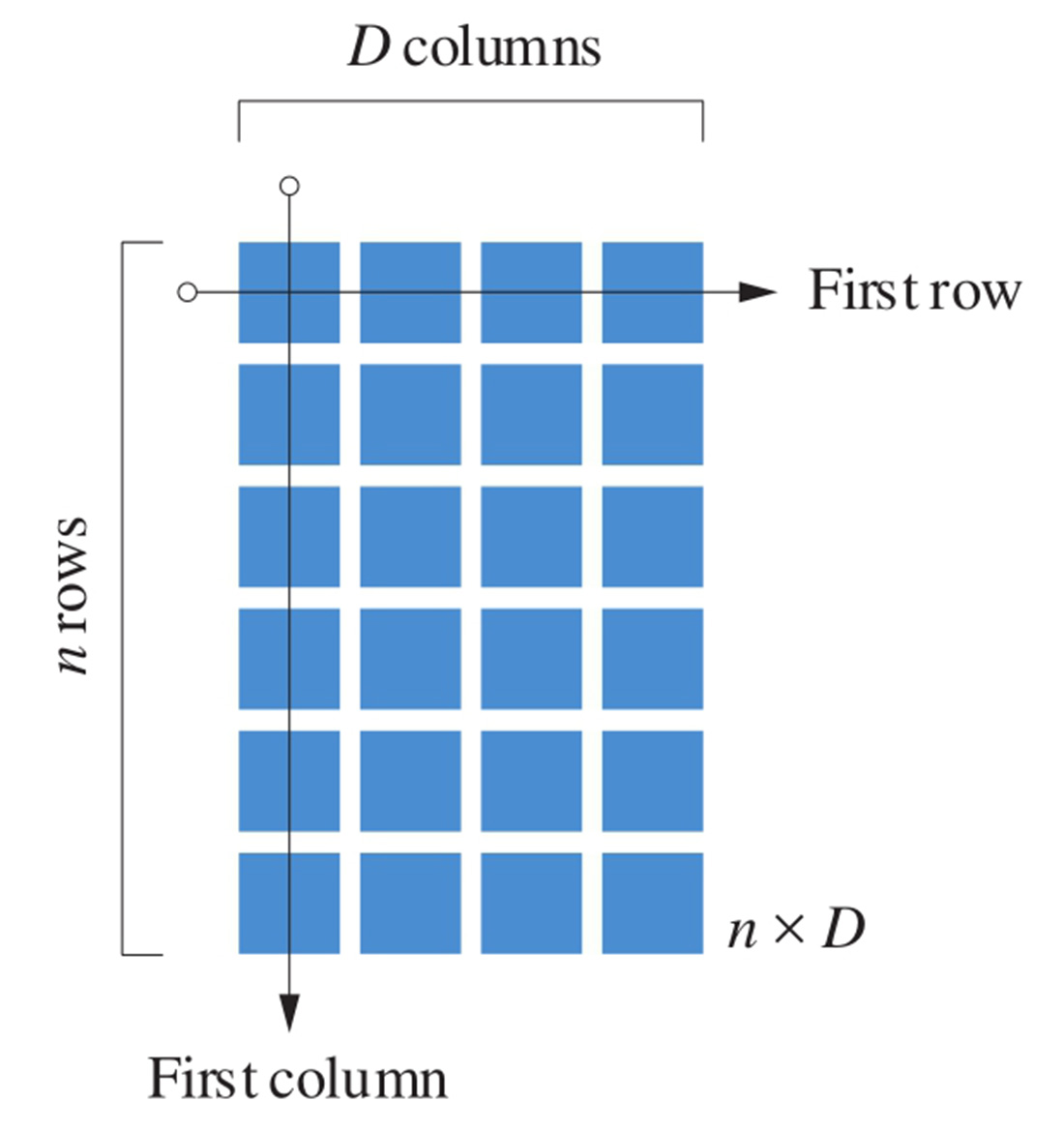
图1.16 n × D 矩阵 X
再次强调：先说行序号，再说列序号。鸢尾花书中，数据矩阵一般采用大写、粗体、斜体 X 表达。
矩阵 X 中， 元素 （element） x i,j 被称作 i,j 元素（ i j entry或 i j element），也可以说 x i,j 出现在 i 行 j 列（appears in row i and column j ）。比如， x n ,1 是矩阵 X 的第 n 行、第1列元素。
表1.4总结了如何用英文读矩阵和矩阵元素。
表1.4 矩阵有关英文表达
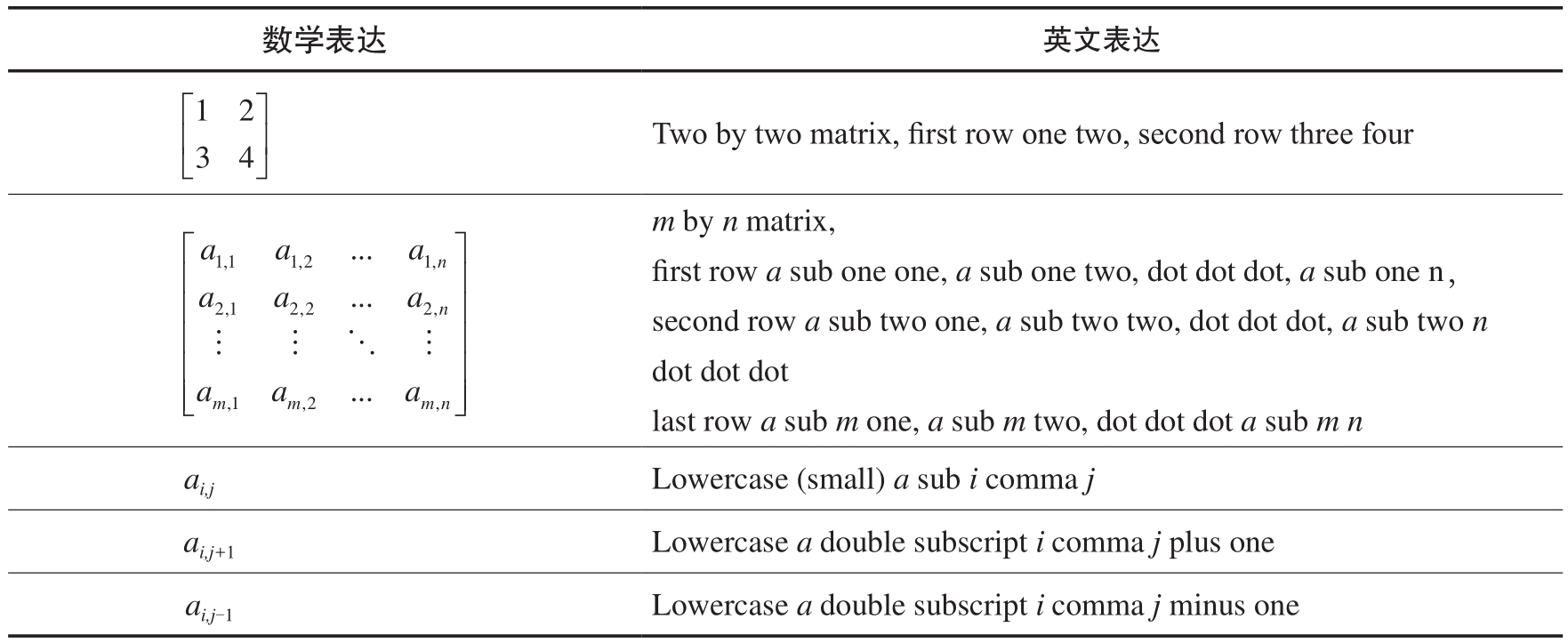
Bk3_Ch1_09.py利用numpy.array（）定义矩阵，并提取矩阵的某一列、某两列、某一行、某一个位置的具体值。
绝大多数情况，数据以矩阵形式存储、运算。举个例子，图1.17所示的鸢尾花卉数据集，全称为 安德森鸢尾花卉数据集 （Anderson’s Iris data set），是植物学家 埃德加·安德森 （Edgar Anderson）在加拿大魁北克加斯帕半岛上采集的150个鸢尾花样本数据。这些数据都属于鸢尾属下的三个亚属。每一类鸢尾花收集了50条样本记录，共计150条。
图1.17中数据第一列是序号，不算作矩阵元素。但是它告诉我们，鸢尾花数据集有150个样本数据，即 n =150。紧随其后的是被用作样本定量分析的四个特征—— 花萼长度 （sepal length）、 花萼宽度 （sepal width）、 花瓣长度 （petal length）和 花瓣宽度 （petal width）。
图1.17中表格最后一列为鸢尾花分类，即 标签 （label）。三个标签分别为—— 山鸢尾 （setosa）、 变色鸢尾 （versicolor）和 维吉尼亚鸢尾 （virginica）。最后一列标签算在内，矩阵有5列，即 D =5。
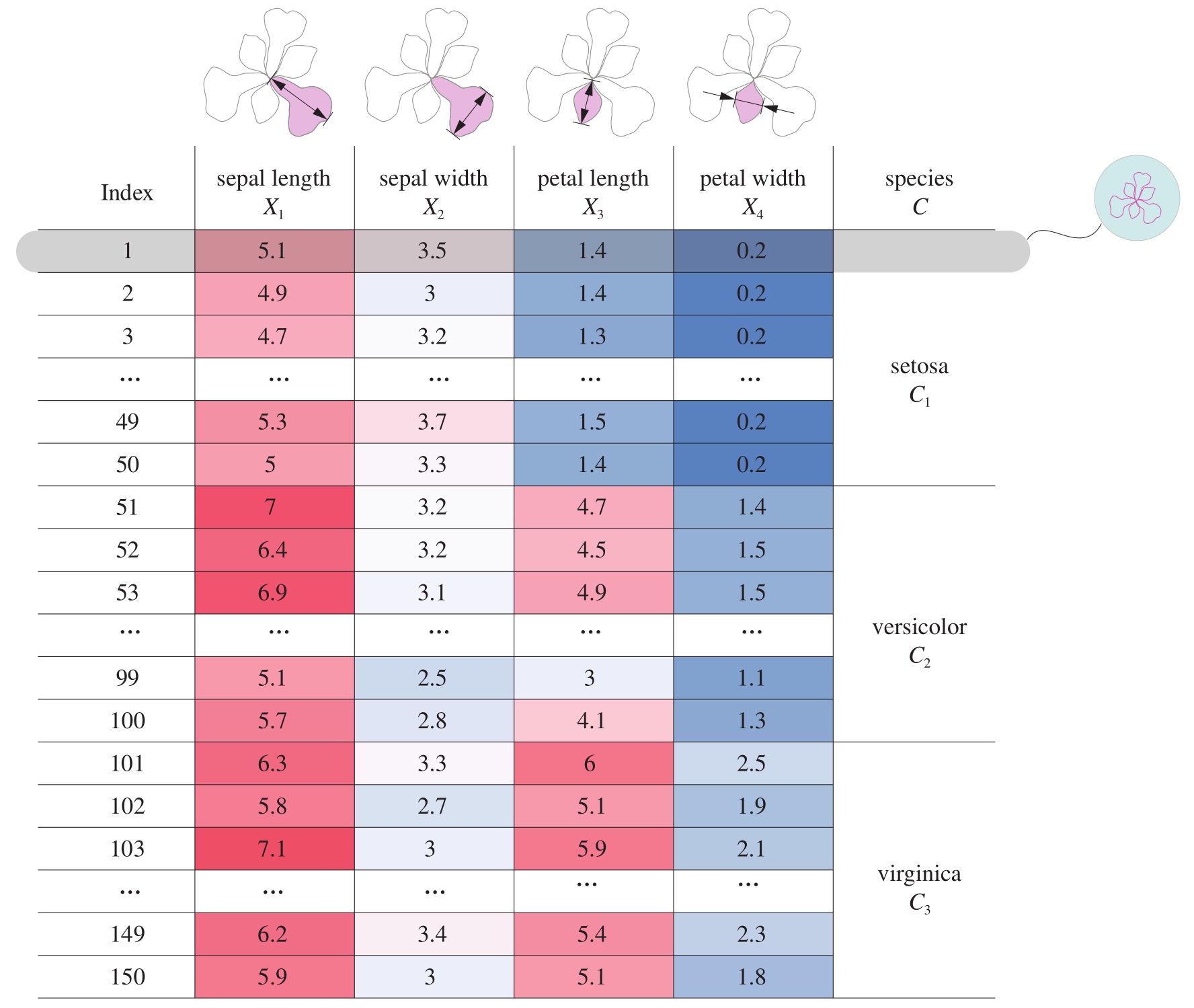
图1.17 鸢尾花数据表格（单位：cm）
这个150×5的矩阵的每一列，即列向量为鸢尾花一个特征的样本数据。矩阵的每一行，即行向量，代表某一个特定的鸢尾花样本。
鸢尾花数据集可以说是鸢尾花书最重要的数据集，没有之一。我们将用各种数学工具从各种视角分析鸢尾花数据。图1.18所示给出了几个例子，鸢尾花书会陪着大家理解其中每幅图的含义。
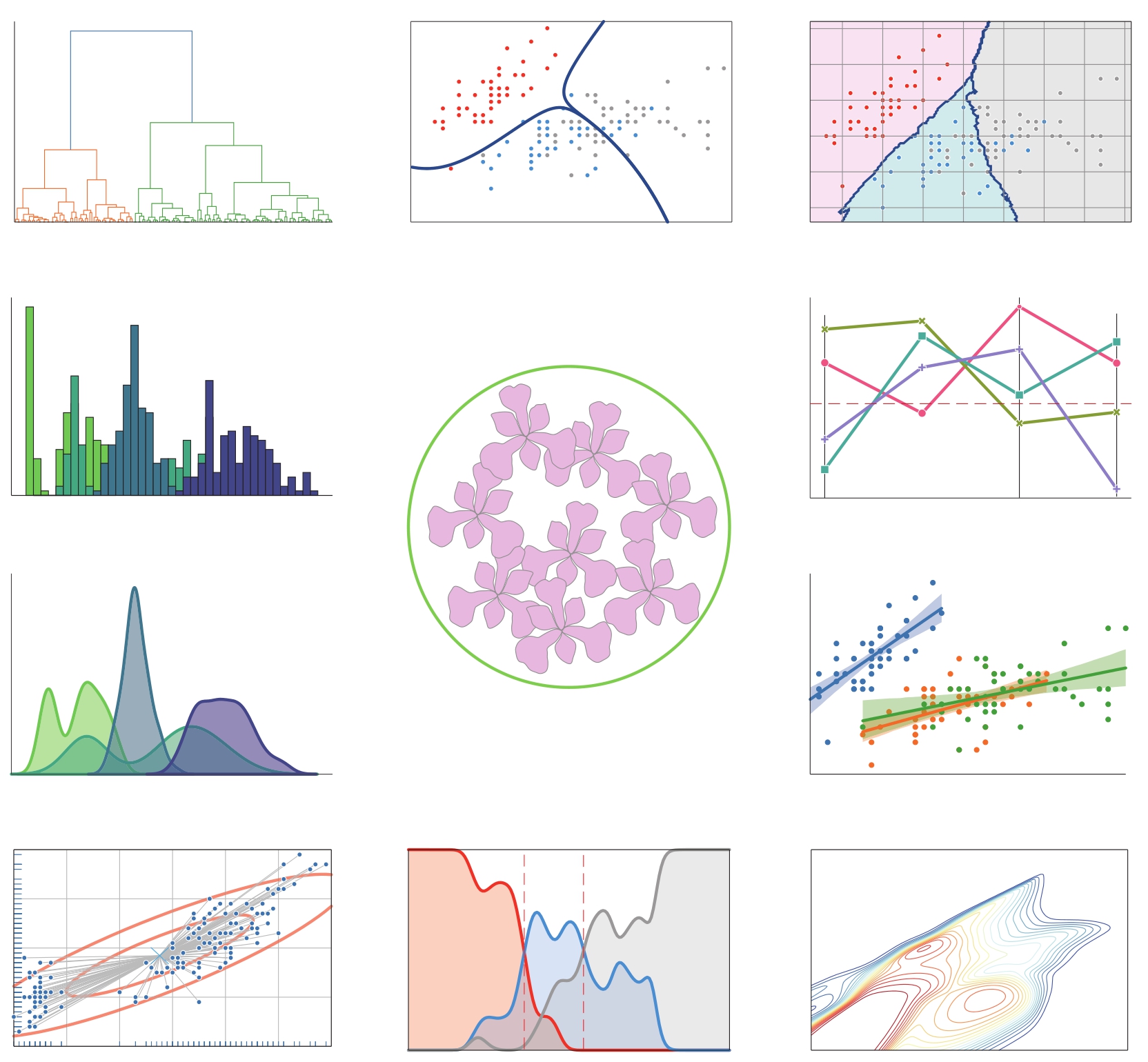
图1.18 用各种概率统计、数据科学、机器学习工具分析鸢尾花数据
大部分数学教科书表达矩阵形状时采用 m × n ；鸢尾花书表达矩阵形状时，一般用 n × D ， n 表示行数， D 表示列数。
采用 n × D 这种记号有以下几方面的考虑。
首先 m 和 n 这两个字母区分度不高。两者长相类似，而且发音相近，这会让初学者辨别行、列时有很大疑惑。而 n 和 D ，一个小写字母，一个大写字母，且发音有显著区别，很容易辨识。
此外，在处理数据时大家会发现，比如pandas.DataFrame定义的数据帧中，列代表特征，如性别、身高、体重、年龄等；行一般代表样本，如小张、小王、小姜等。而统计中，一般用 n 代表样本数，因此决定用 n 来代表矩阵的行数。字母 D 取自dimension（维度）的首字母，方便记忆。
鸢尾花书横跨代数、线性代数、概率统计几个板块， n × D 这种记法方便大家把矩阵运算和统计知识联系起来。
本书编写之初，也有考虑用feature（特征）的首字母 F 来表达矩阵的列数，但最终放弃。一方面，是因为鸢尾花书后续会用 F 代表一些特定函数；另一方面， n 和 F 的发音区分度不如 n 和 D 那么高。
基于以上考虑，鸢尾花书后续在表达样本数据矩阵形状时都会默认采用 n × D 这一记法，除非特别说明。
矩阵可以看做是，若干列向量左右排列，或者若干行向量上下叠放。比如，形状为2×3的矩阵可以看成是3个列向量左右排列，也可以看成是2个行向量上下叠放，如
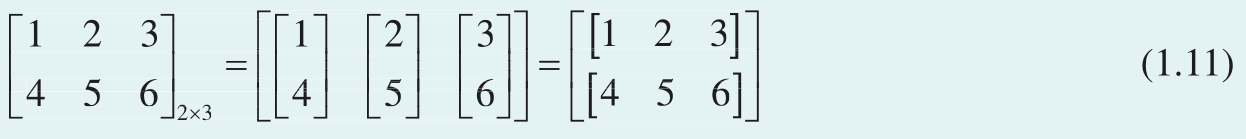
一般情况下，如图1.19所示，形状为 n × D 的矩阵 X ，可以写成 D 个左右排列的列向量，即
X 也可以写成 n 个行向量上下叠放，即
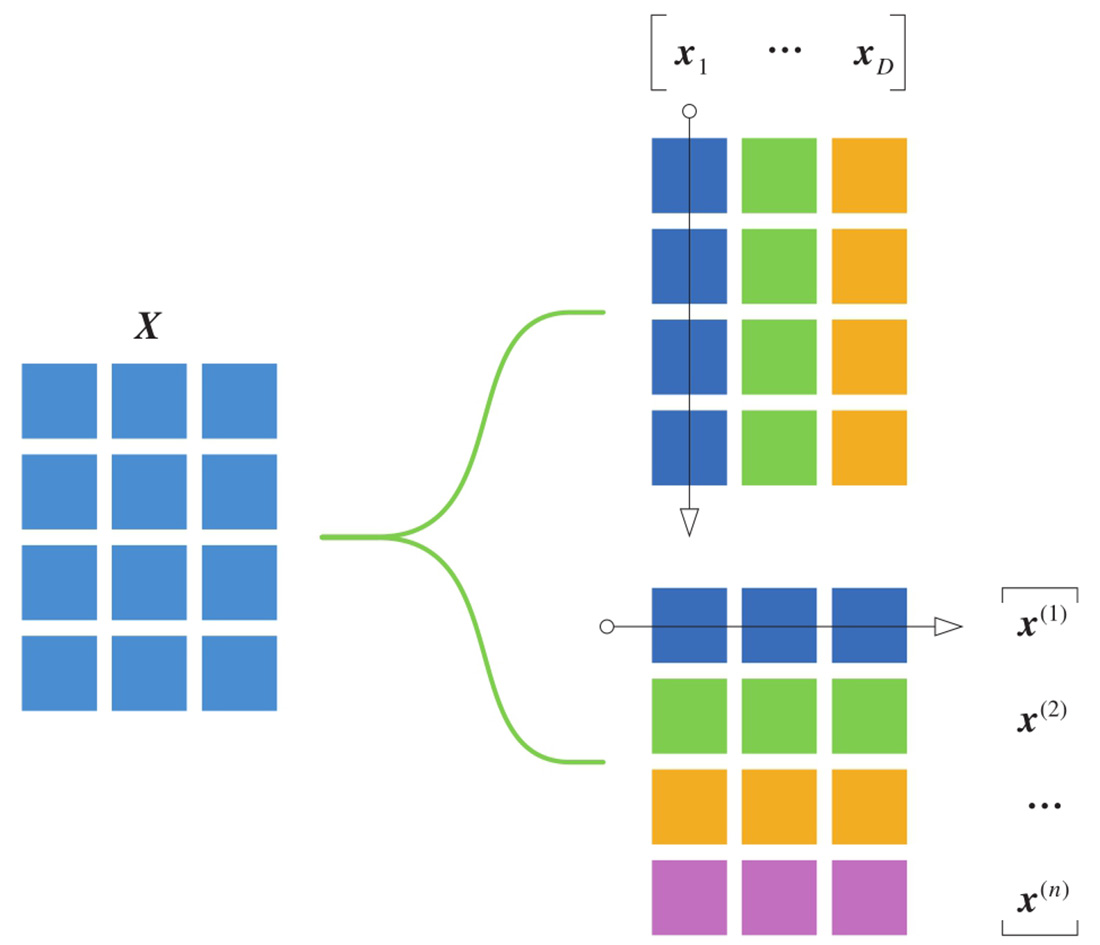
图1.19 矩阵可以分解成一系列行向量或列向量
实际上，式（1.12）和式（1.13）蕴含着一种重要的思想——矩阵分块（block matrix或partitioned matrix）。鸢尾花书《矩阵力量》一册会详细介绍矩阵分块及相关的运算规则。
注意：为了区分含序号的列向量和行向量，鸢尾花书将列向量的序号写成下角标，比如 x 1 、 x 2 、 x i 、 x D 等；将行向量的序号写成上角标加圆括号，比如 x （1） 、 x （2） 、 x （ j ） 、 x （ n ） 等。列索引一般用 i ，行索引一般用 j 。
矩阵转置 （matrix transpose）指的是将矩阵的行列互换得到的新矩阵，如
式（1.14）中，3×2矩阵转置得到矩阵的形状为2×3。
图1.20所示为矩阵转置示意图，其中红色线为 主对角线 （main diagonal）。
再次强调，主对角线是从矩阵第1行、第1列元素出发向右下方倾斜45°斜线。
转置前后，矩阵主对角线元素位置不变，如式（1.14）的1、4两个元素。向量转置是矩阵转置的特殊形式。
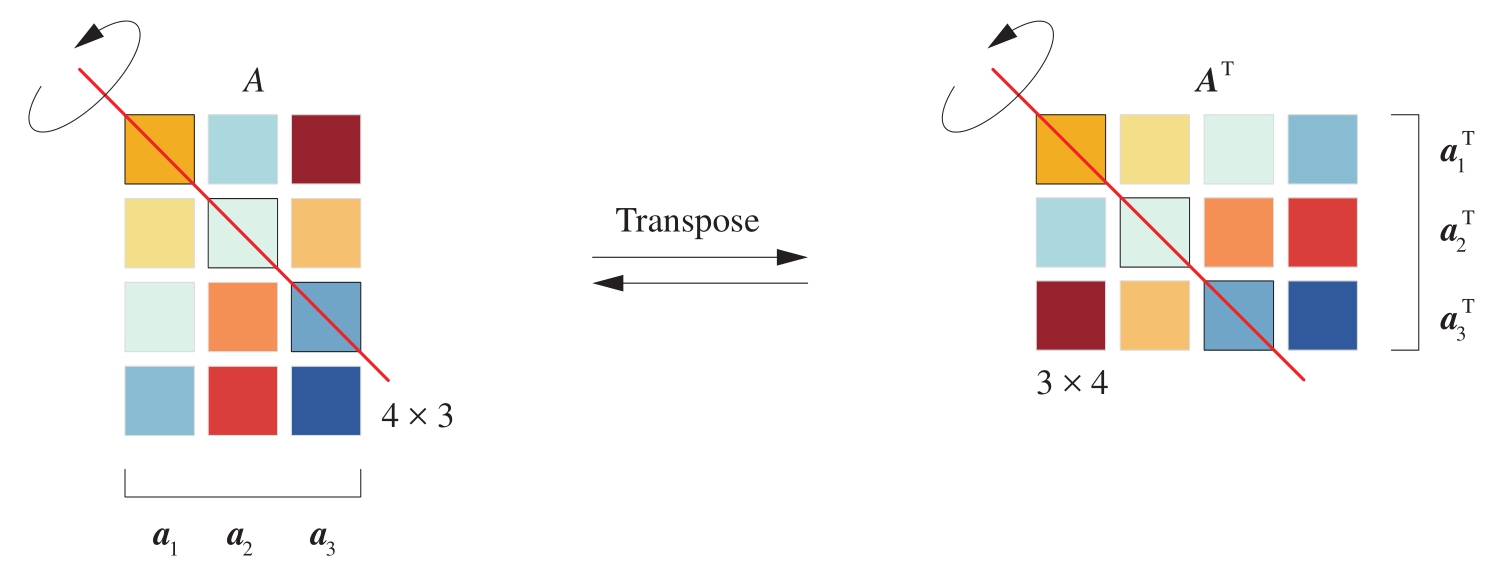
图1.20 矩阵转置
如图1.20所示，将矩阵 A 写成三个列向量左右排列[ a 1 , a 2 , a 3 ]，对 A 转置得到的结果为
这一点对于转置运算非常重要，再举个具体例子。给定以下矩阵，并将其写成左右排列的列向量。
式（1.16）矩阵转置结果为
反之，将矩阵 A 写成三个行向量上下叠放，对 A 转置得到的结果为
请大家根据上式，代入具体值自行完成类似式（1.17）的验算。
矩阵的一般形状为长方形，但是矩阵还有很多特殊形状。图1.21所示为常见的特殊形态矩阵。
很明显，列向量、行向量都是特殊矩阵。
如果列向量的元素都为1，一般记作 1 。 1 被称作全1列向量，简称 全1向量 （all-ones vector）。
如果列向量的元素都是0，这种列向量叫作 零向量 （zero vector），记作 0 。
行数和列数相同的矩阵叫 方阵 （square matrix），如2×2矩阵。
对角矩阵 （diagonal matrix）一般是一个主对角线之外的元素皆为0的方阵。
单位矩阵 （identity matrix）是主对角线元素为1其余元素均为0的方阵，记做 I 。
对称矩阵 （symmetric matrix）是元素相对于主对角线轴对称的方阵。
零矩阵 （null matrix）一般指所有元素皆为0的方阵，记做 O 。
每一种特殊形状矩阵在线性代数舞台上都扮演着特殊的角色，鸢尾花书会慢慢讲给大家。
值得注意的是，大家会在鸢尾花书《矩阵力量》一本中发现，对角矩阵也可以不是方阵。此外，零矩阵也未必都是方阵。
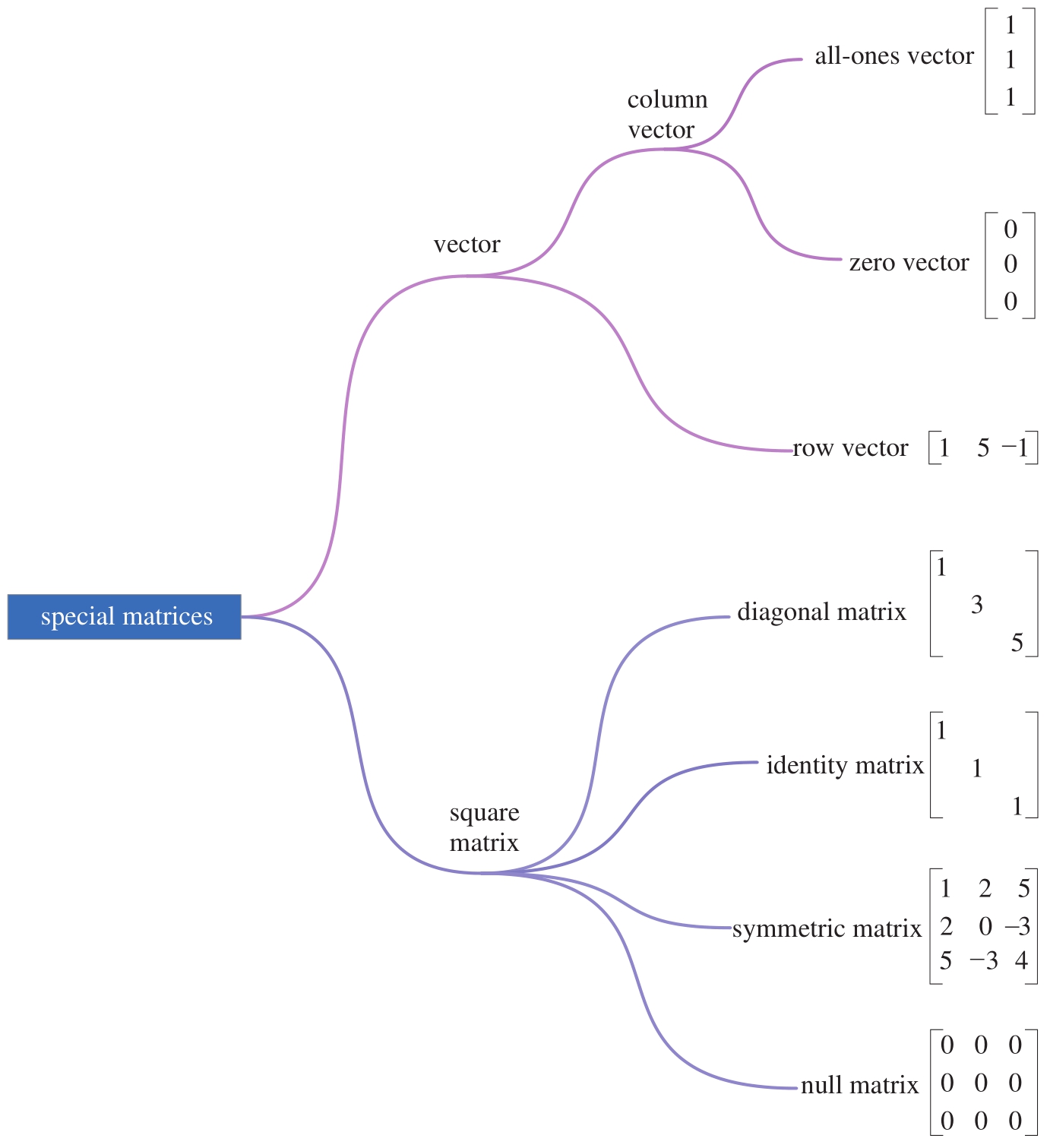
图1.21 常见特殊形态矩阵
本节介绍矩阵加减法。矩阵相加减就是批量化完成若干加减运算。矩阵加减可以视作四则运算中加减的高阶版本。
上一节说过，行向量和列向量是特殊的矩阵。两个等长的行向量相加，为对应元素相加，得到还是一个行向量，如
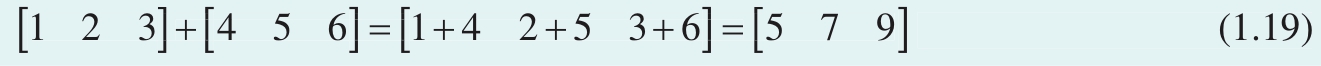
同理，两个等长行向量相减，就是对应元素相减，得到的也是相同长度的行向量，如
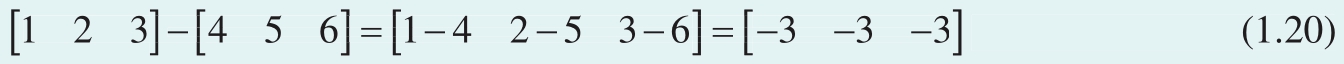
式（1.19）和式（1.20）相当于一次性批量完成了三个加减法运算。
同理，两个等长的列向量相加，得到的仍然是一个列向量，如
图1.22所示为两个数字相加的示意图。图1.23所示为向量求和。
注意：两个矩阵能够完成加减运算的前提——形状相同。
图1.22 数字求和
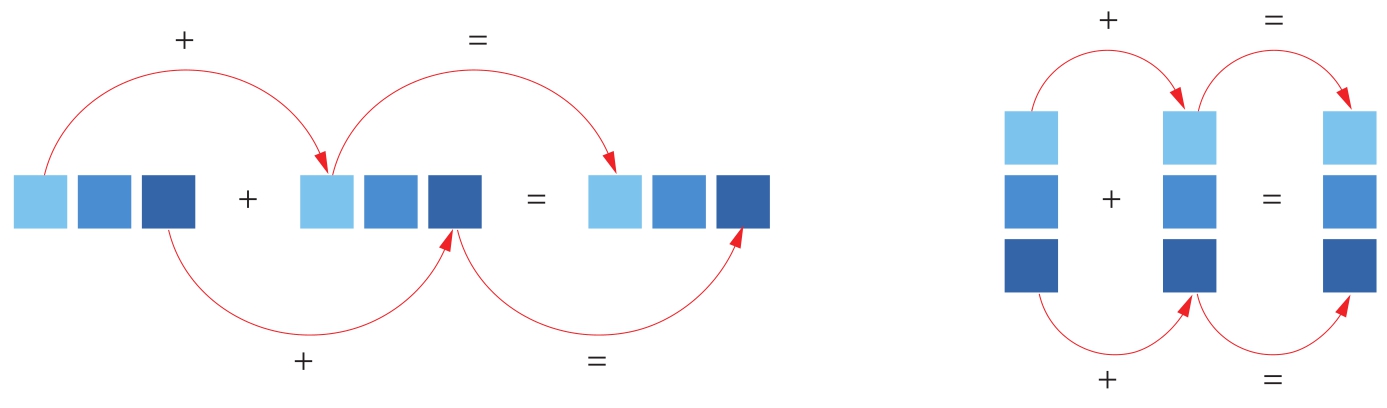
图1.23 向量求和
Bk3_Ch1_10.py展示了四种计算行向量相加的方式。这四种方法中，当然首推使用NumPy。
形状相同的两个矩阵相加的结果还是矩阵。运算规则为，对应位置元素相加，形状不变，如
两个矩阵相减的运算原理完全相同，如
Bk3_Ch1_11.py用for循环完成矩阵加法运算，这种做法并不推荐！Bk3_Ch1_12.py利用NumPy完成矩阵加法。
注意：用for循环来解决矩阵相加是最费力的办法，比如Bk3_Ch1_11.py代码给出的例子。为了让代码运算效率提高，常用的方法之一就是——向量化（vectorize）。也就是说，尽量采用向量／矩阵运算，以避免循环。
数字和数学是抽象的，它们是人类总结的规律，是人类思想的产物。
“双兔傍地走”中的“双”就是2；2这个数字对人类有意义，对兔子自身没有意义；两只兔子自顾自地玩耍，一旁暗中观察的某个人在大脑中思维活动抽象产生了“双”这个数字概念，而且要进一步“辨雄雌”。
试想一个没人类的自然界。那里，天地始交，万物并秀，山川巍峨，江河奔涌，雨润如酥，暗香浮动，芳草萋萋，鹿鸣呦呦，鹰击长空，鱼翔浅底。
试问，这般香格里拉的梦幻世界和数字有什么关系？
然而，本书的读者很快就知道，微观世界中，自然界中，天体运行中，人类通过几千年的观察研究发现，数字、数学规律无处不在；只是天意从来高难问，大部分规律不为人所知罢了。
这让我们不禁追问，可感知世界万物是否仅仅是表象？世界万物创造动力和支配能量，是否就是数字和数学？我们听到的、看到的、触摸到的，是否都是数字化的，虚拟化的？整个物质世界仅仅是某个巨型计算机模拟的产物吗？这些问题让我们不寒而栗。
老子说：“大道无形，生育天地；大道无情，运行日月。”老子是否真的参透了世间万物？他口中的“大道”是否就是数字、数学规律？
推荐一本机器学习数学基础的好书， Mathematics for Machine Learning ，剑桥大学出版社。这本书给了本书很多可视化灵感。该书作者提供全书免费下载，地址为：
◄ https://mml-book.github.io/book/mml-book.pdf
这本书横跨线性代数、微积分、概率统计三大板块。对于基础薄弱的读者，读这本书可能会存在很多困难。大家学完“鸢尾花书”数学板块的《数学基础》《矩阵力量》《统计至简》三册之后，大家就会发现 Mathematics for Machine Learning 变得好读多了。