




在绘制素描前,要对物体的透视规律进行分析,以便获得更加准确的画面效果。
生活中我们常常会发现:路面向远处延伸时越来越窄,道路两旁的树木越往远处越小……这些都涉及本小节要介绍的近大远小的基本透视规律。下面让我们先了解一下这些基本的透视规律。
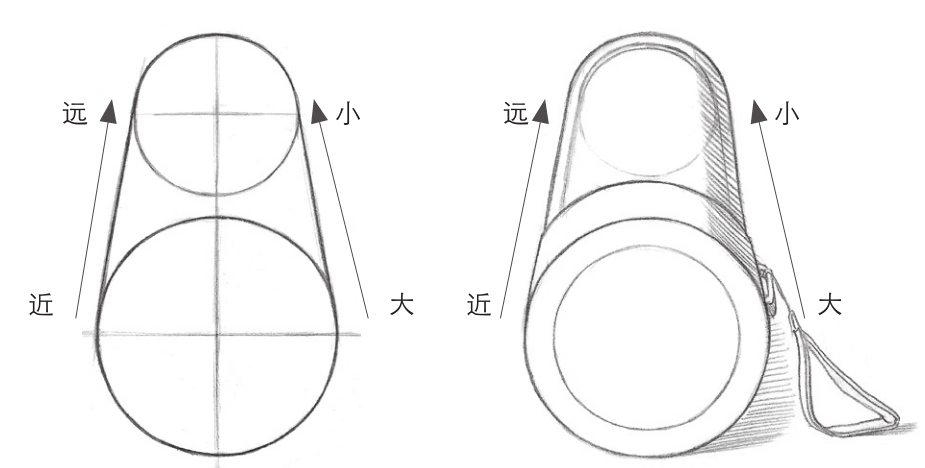
单个物体的透视规律最明显的就是近大远小,此效果表现起来较为简单,也比较容易掌握。简单的几何体就能体现近大远小的透视规律。
杯子可以看作圆柱体,从左图可以看出,离视点近的顶面要比底面大一些,体现出了近大远小的规律。
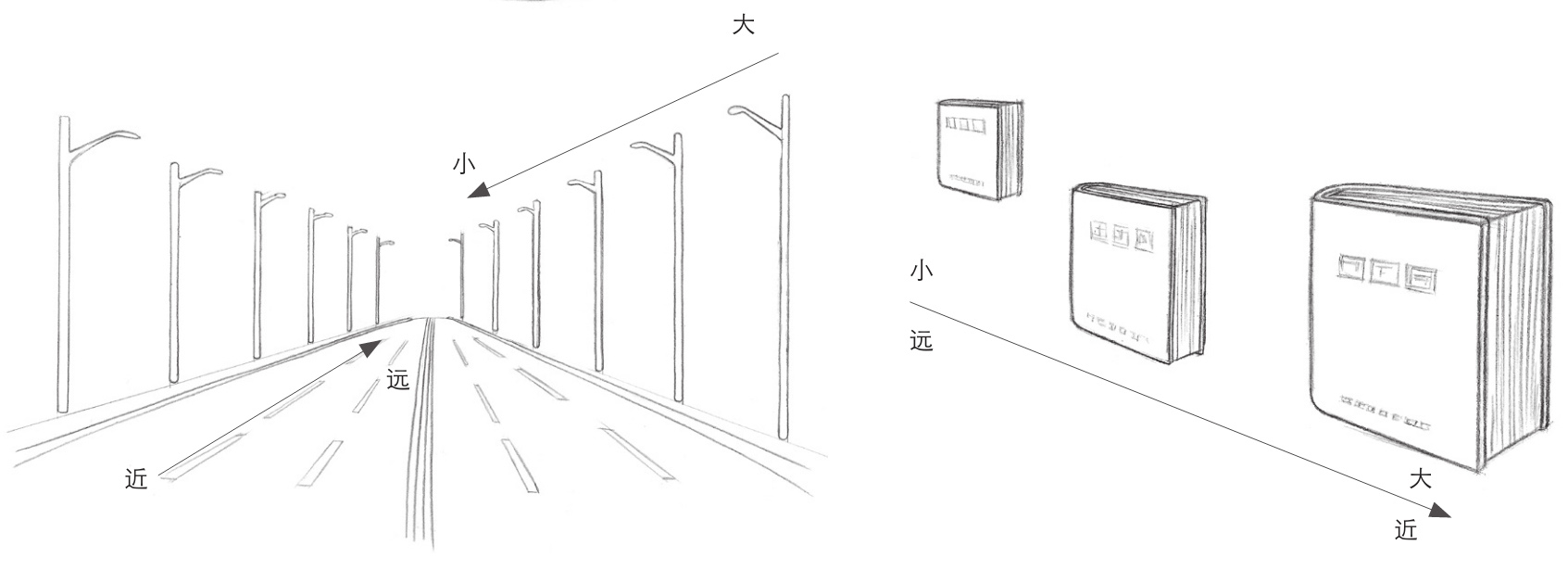
多个物体有规律地排列时,在视觉上会形成近大远小的透视规律;从上面的左图中路边路灯的排列可以看出,靠近视点的路灯大一些,远离视点的路灯较小;上面右图的透视规律也是如此。
平行透视也称“一点透视”,是指在60°视域中观察立方体上下、前后及两侧6个面时,不论立方体在什么位置,只要有一个面与可视画面平行,立方体和画面形成的透视规律就是“平行透视”。
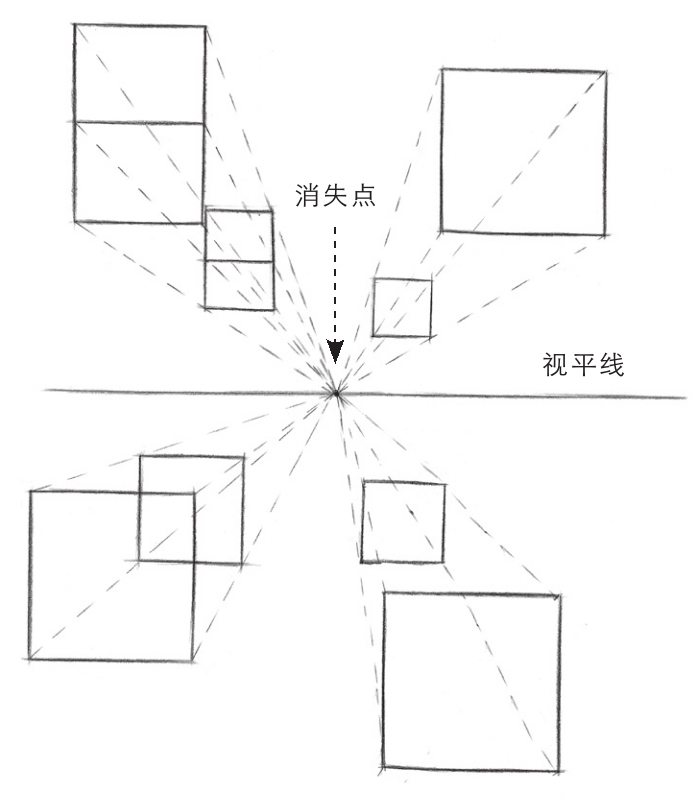
成角透视也称“两点透视”,是指把立方体画到画面上,立方体的4个垂直面相对画面倾斜一定角度时,在视平线上产生了两个消失点。在这种情况下,与上下两个水平面垂直的平行线的长度产生了变化,但是没有消失点。
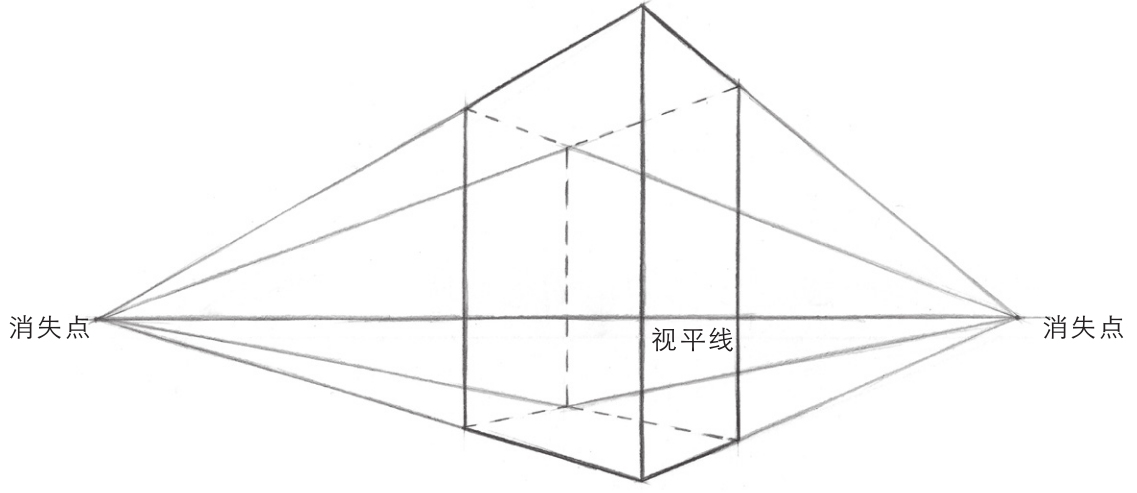
成角透视有两个消失点,分别在视平线的两端;而且成角透视的垂直线永远垂直,只有近大远小的变化。
三点透视也称“倾斜透视”,是各种透视中视觉冲击力最强的一种透视,一般用于表现超高层建筑俯瞰图或仰视图。三点透视的画面中有3个消失点,其中有两个消失点在视平线上,还有一个消失点视平线以外。
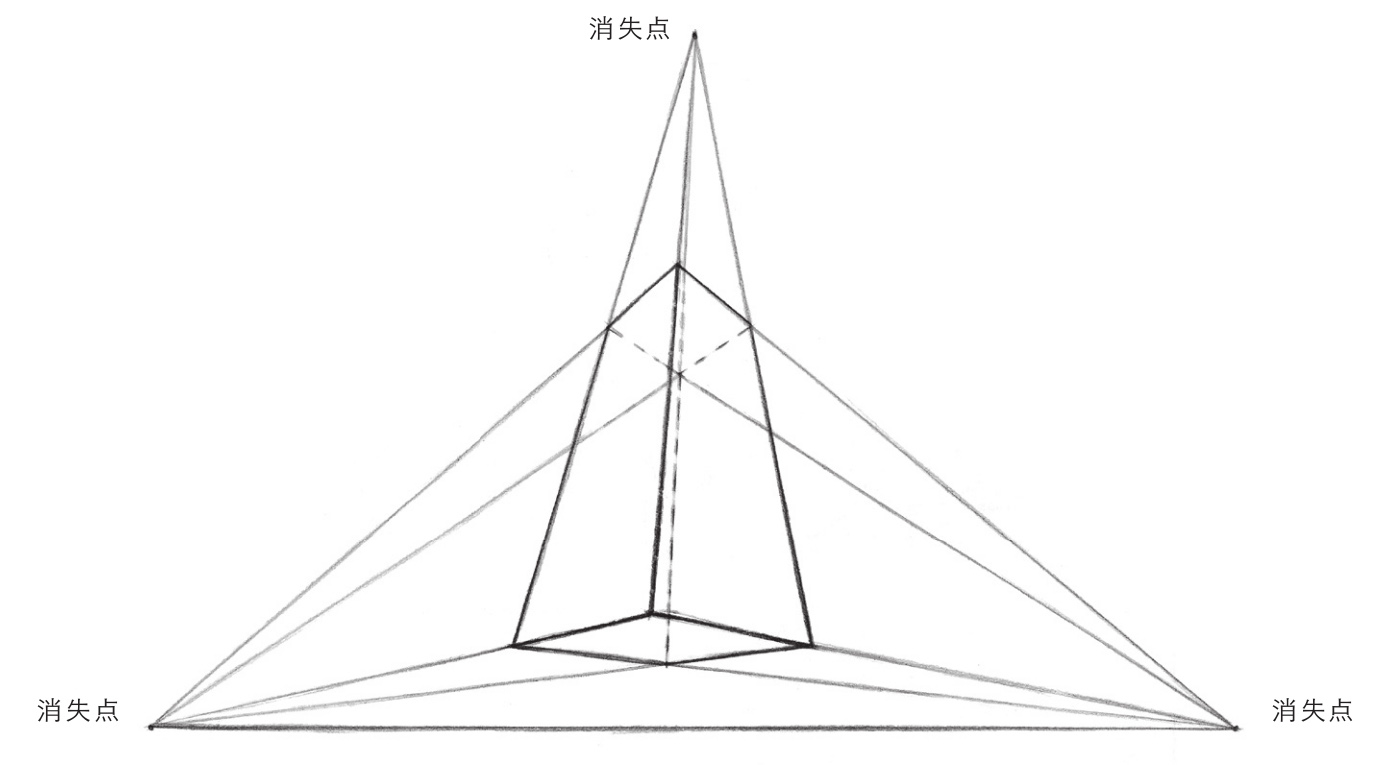
三点透视中,视平线以外的消失点采用在高度上取消失点的方法来表现。由于建筑物除左右进深外,又增加了上下进深,因此这种透视不仅可以使建筑物更加富有立体感,而且也增加了画面的空间感、纵深感,使画面看上去很有“气势”。
前面讲的透视都是基于由直线构成的物体,用它来说明基本规律容易理解,但是客观事物中大多数物体是由规则的曲线(圆形、椭圆形等)构成的。
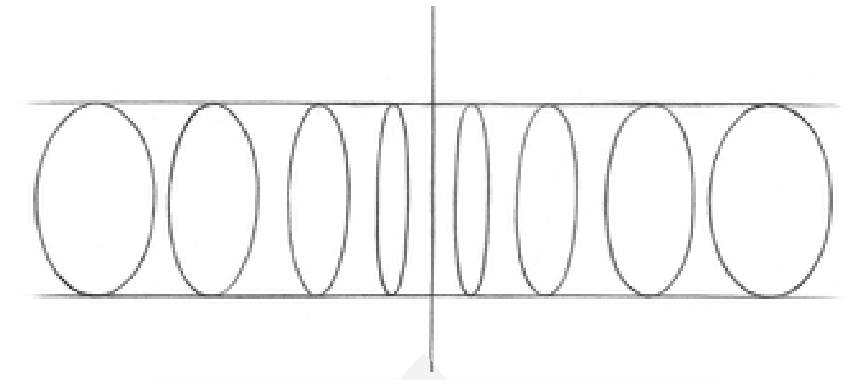
圆形经透视变形后变为椭圆形。与地面和画面垂直的圆形,位置越接近中线,其透视变形的程度越大。
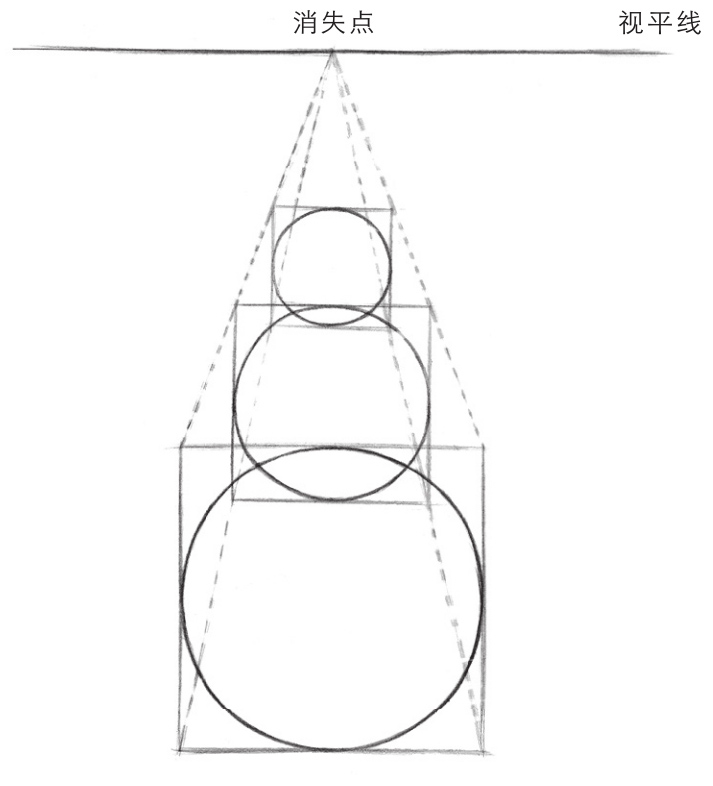
与画面平行的圆形,无论远近,都保持着本来的形状,只有近大远小的变化。