




逻辑之所以被称为“形式的”,是因为它关注的不是陈述的内容,而是陈述的形式。陈述由主语、谓语及且、或、所有、存在、如果、那么等逻辑词汇组合而成。

通常,我们对自己所关心的内容运用逻辑,例如“美国总统因叛国、贿赂或其他重罪和轻罪被弹劾而判罪者,应予罢免”。我们据此推断,要罢免总统,他不仅要被弹劾,还要被判罪,他不需要同时被判叛国罪和贿赂罪,一个就足够了。但是逻辑的法则是通用的:它们适用于任何内容,不管内容是明确的还是模糊的,甚至无意义的内容也可以。基于这一点,刘易斯·卡罗尔在他1896年出版的教材《符号逻辑》(
Symbolic Logic
)中创造了“愚蠢三段论”(sillygism)
 这个概念,这本教材的许多内容至今仍在逻辑课程中被引用。例如,从前提“如果你借给瘸腿的小狗一根跳绳,它不会对你说‘谢谢’”和“你借给这只小狗一根跳绳”,人们可以推断出“这只小狗没有说‘谢谢’”。
这个概念,这本教材的许多内容至今仍在逻辑课程中被引用。例如,从前提“如果你借给瘸腿的小狗一根跳绳,它不会对你说‘谢谢’”和“你借给这只小狗一根跳绳”,人们可以推断出“这只小狗没有说‘谢谢’”。

逻辑系统被形式化为规则,有了这些规则,人们就可以通过替换一系列符号而从先前的陈述推导出新的陈述。最基本的逻辑系统是命题演算,演算在拉丁语中是“卵石”的意思。这个术语告诉我们,逻辑就是机械地操纵符号,而不用管内容。简单的句子被简化为变量,如P和Q,它们跟真值有关联:要么为真,要么为假。简单陈述通过逻辑连接词且、或、非和如果–那么组合为复杂陈述。
你甚至不需要知道逻辑连接词在文中的意思。它们的意义仅在于明确一些规则,这些规则告诉我们一个复杂陈述的真假,取决于它所包含的那些简单陈述的真假。这些规则通过图3-1中的真值表得到定义。其中a图是定义“且”规则的,可以逐行解释,类似这样:当P为真、Q也为真时,意味着“P且Q”为真;当P为真、Q为假时,意味着“P且Q”为假;最后两行也可以做类似的解释。b图与c图分别定义了“或”规则与“非”规则。
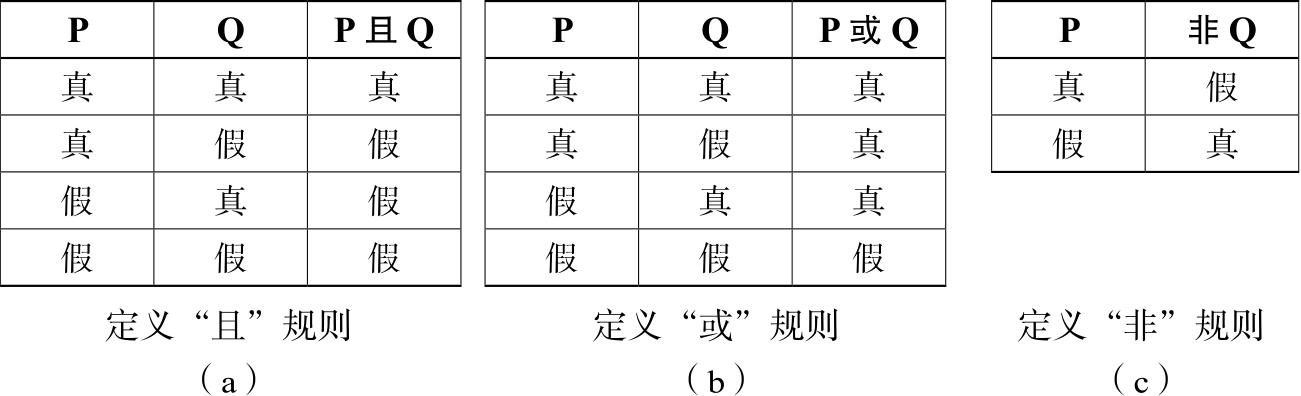
图3-1 定义“且”“或”“非”规则的真值表
我们举一个例子。在1970年的浪漫悲剧电影《爱情故事》( Love Story )的开场中,詹妮弗·卡维列里(Jennifer Cavilleri)向哈佛大学的学生、她傲慢地称之为“预科生”的奥利弗·巴雷特四世(Oliver Barrett IV)解释,为什么她认为后者上过预科学校:“你看上去既笨又富有。”让我们把“奥利弗很笨”标为P,把“奥利弗很富有”标为Q。只有“且”规则真值表第1行列出的那些简单事实均为真,她对奥利弗的奚落才成立。奥利弗抗议道(说的不完全是真话):“实际上,我聪明但很穷。”我们假设“聪明”的意思是“非笨”,“穷”的意思是“非富有”。我们知道奥利弗在引用同一个真值表的第4行来反驳她:如果奥利弗不笨也不富有,那么他就不是“既笨又富有”了。如果只是想反驳詹妮弗,他也可以这么说,“实际上,我聪明又富有”(第3行)或“实际上,我又笨又穷”(第2行)。不过实际情况是,奥利弗并不穷,他在说谎,这意味着他的“聪明但很穷”的说法是错的。
詹妮弗诚实地回答说:“不,我才既聪明又穷呢。”假设我们根据剧本得出这样一个愤世嫉俗的推论:“哈佛学生要么有钱,要么聪明。”这个推论不是演绎推理,而是归纳推理,得出的是一个从观察中得出的容易出错的陈述。我们先把“我们是如何得到这个陈述的”这个问题放在一边,现在来看看这个陈述本身,问问是什么使它为真。这是一个析取式,一个带有“或”的陈述,把这对恋人的相关信息带入中间的那个“或”的真值表,就可以验证这一陈述的真假。P代表“富有”,Q代表“聪明”。詹妮弗很聪明,尽管她并不富有(第3行);奥利弗很富有,尽管他可能聪明也可能不聪明(第1行或第2行),所以,上面那个关于哈佛学生的析取陈述,至少在这两个人身上为真。
两人继续开着玩笑:
奥利弗:你为什么这么聪明?
詹妮弗:我不会跟你去喝咖啡的。
奥利弗:我不会邀请你喝咖啡的。
詹妮弗:这就是你笨的原因。
让我们把詹妮弗的回答写成:“如果你邀请我喝咖啡,我会说‘不’。”根据我们所掌握的信息,这一陈述为真吗?这是一个条件句,一个由“如果(前件)”和“那么(后件)”构成的语句。它的真值表是什么呢?回想一下沃森选择任务(第1章),“如果P,那么Q”为假的唯一方式是当P为真而Q为假。“如果一封邮件贴上了特快专递的标签,那么它必须贴上一张10美元的邮票。”意思是没有10美元邮票的特快专递是不可能的。其真值表如图3-2所示。
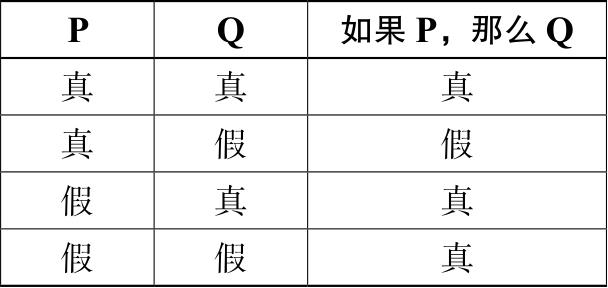
图3-2 沃森选择任务的真值表
如果我们相信这两人说的话,那就是奥利弗不会邀请詹妮弗喝咖啡。换句话说,代表着“你邀请我喝咖啡”的P是假的,这意味着詹妮弗的如果-那么陈述是真的(图3-2第3列的第3行和第4行)。真值表告诉我们,奥利弗给詹妮弗的回复是无关紧要的:只要奥利弗没有邀请她喝咖啡,她说的就是真话。按调情场景的套路,奥利弗最终还是邀请她喝咖啡了(P从假变成了真),她也接受了(代表着“我会说‘不’”的Q为假)。这意味着她的条件陈述“如果P,那么Q”为假,开玩笑通常都是如此。
刚刚进行的讨论告诉我们,逻辑真是挺奇妙的:只要一个条件句的前件为假,整个条件句就为真(只要奥利弗没有邀请詹妮弗喝咖啡,詹妮弗说的就是真话)。这就是说,逻辑上的条件句,不同于日常谈话中带有“如果”和“那么”的陈述句。一般来说,我们用条件句表示有根据的预测,这个预测基于一则可检验的因果律,比如“如果你喝咖啡,你会保持清醒”。但是,如果把从未经过检验的一个条件句判定为真,我们是不会满意的。比如“如果你喝了芜菁汁,就会保持清醒”这种说法,如果你从未喝过芜菁汁,那么这个条件句从逻辑上来看就是正确的。我们希望有理由相信在P为真,也就是你喝了芜菁汁的反事实情境下,非Q,也就是你睡着了这件事不会发生。当一个条件句的前件已知为假或必然为假,我们会忍不住说这个条件句发生的可能性不大,因而不用去考虑它,或者说它是无关紧要的或仅仅是推测性的,甚至是无意义的,而不会说这个条件句为真。但从真值表所规定的逻辑意义上来说,“如果P,那么Q”跟“非‘P且非Q’”是一个意思,那么奇怪的推论就会出现:“如果猪有翅膀,那么2+2=5”为真,“如果2+2=3,那么2+2=5”也为真。因此,逻辑学家用一个技术术语来命名真值表意义上的条件句,即“实质条件句”(material conditional)。
这里有一个真实的例子,可以说明为什么做这种区分很重要。假设我们要给专家的预测准确性打分,我们该如何评估2008年的条件句预测“如果萨拉·佩林(Sarah Palin)成为总统,她将禁止所有堕胎行为”呢?专家赢得名声是因为从逻辑上说这一陈述为真呢,还是说从逻辑和现实两种意义上说都不为真?对于这个从真实预测中提炼出来的例子,打分者必须首先不把它们看作正确的预测,再确定怎样对待它们:他们往往会从日常生活的角度解释这个条件句,而不是在逻辑意义上将其作为一个实质条件句。

日常用语中的“如果”和逻辑意义上的“如果”之间的区别,就是以下事实的案例之一:形式逻辑中起连接作用的逻辑连接符在逻辑中的使用方式与日常交谈中的使用方式是不一样的。在日常生活中,一个词可能有多种含义,只有通过上下文才能知道其确切的含义。
 当我们听到“他坐下来并给我讲他的生活故事”这句话时,我们会把“并”这个词理解成他先做了第一个动作,然后又做了第二个动作。尽管从逻辑意义上来说,顺序也可能是反过来的。比如,曾流传过这样一个俏皮话:“他们结婚了,并生了个孩子,但顺序不是这样的。”当抢劫犯说“你要钱还是要命”时,从技术层面来说,这两样东西你都可以要,因为“P或Q”包含了“P为真且Q为真”这种情况。不过,你硬要跟他争论这个问题是不明智的。每个人都会将上下文中的“或”理解为逻辑连接符“异或”,也就是P或Q,但不包括“P且Q”。这也是为什么当菜单上写着“汤或沙拉”时,我们并不会与服务员争论,坚称从逻辑上说我们有权同时享用这两种食物。从技术层面来说,像“男孩就是男孩”“交易就是交易”“情况就是这么个情况”“有时雪茄就是雪茄”这样的命题都是空洞的重言式
当我们听到“他坐下来并给我讲他的生活故事”这句话时,我们会把“并”这个词理解成他先做了第一个动作,然后又做了第二个动作。尽管从逻辑意义上来说,顺序也可能是反过来的。比如,曾流传过这样一个俏皮话:“他们结婚了,并生了个孩子,但顺序不是这样的。”当抢劫犯说“你要钱还是要命”时,从技术层面来说,这两样东西你都可以要,因为“P或Q”包含了“P为真且Q为真”这种情况。不过,你硬要跟他争论这个问题是不明智的。每个人都会将上下文中的“或”理解为逻辑连接符“异或”,也就是P或Q,但不包括“P且Q”。这也是为什么当菜单上写着“汤或沙拉”时,我们并不会与服务员争论,坚称从逻辑上说我们有权同时享用这两种食物。从技术层面来说,像“男孩就是男孩”“交易就是交易”“情况就是这么个情况”“有时雪茄就是雪茄”这样的命题都是空洞的重言式
 ,它们的形式虽然正确,但缺乏内容。但是,我们会将其解读成具有某种意义。比如,“有时雪茄就是雪茄”这个例子(源于西格蒙德·弗洛伊德)可以理解为:雪茄并不总是男性生殖器的象征。
,它们的形式虽然正确,但缺乏内容。但是,我们会将其解读成具有某种意义。比如,“有时雪茄就是雪茄”这个例子(源于西格蒙德·弗洛伊德)可以理解为:雪茄并不总是男性生殖器的象征。
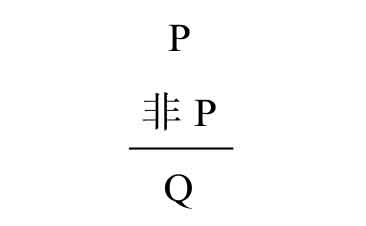
即使这些词被固定在严格的逻辑意义上,如果逻辑仅仅是检验包含逻辑术语的语句是对是错,那么它也只是一个小练习。逻辑的力量来自有效推理的规则:允许你从真前提跳到真结论的小算法。最广为人知的规则是“肯定前件”(affirming the antecedent)。在下面几个例子中,线上是前提,线下是结论。

“如果某个人是女人,那么她终有一死。赞西佩是女人。因此,赞西佩终有一死。”
另一个有效的推理规则被称为“否定后件”(denying the consequent),即换质换位法(the law of centraposition)。

“如果某个人是女人,那么她终有一死。蛇发女妖丝西娜
 是永生不死的。因此,蛇发女妖丝西娜不是女人。”
是永生不死的。因此,蛇发女妖丝西娜不是女人。”
这些规则是最广为人知的,但并不是说有效的推理规则就只有这些。从亚里士多德第一次将逻辑形式化,到19世纪末开始的逻辑数学化,逻辑基本上就是对推理方法的分类,人们通过这些方法从前提集中推导出结论。例如,有一个有效的、但多数情况下无用的析取加法。

“巴黎在法国。因此,巴黎在法国或独角兽确实存在。”
还有一种更有用的析取三段论,或称之为排除法。

“受害者是被人用铅管或烛台杀死的。受害者不是被人用铅管杀死的。因此,受害者是被人用烛台杀死的。”据说,逻辑学家悉尼·摩根贝瑟(Sidney Morgenbesser)和他的妻子接受了婚姻咨询,在咨询期间,这对争吵不休的夫妇不停地抱怨对方。恼怒的咨询师最后对他们说:“现在,必须有人要做出改变。”摩根贝瑟回答说:“好吧,我不会改变,她也不会改变,所以你必须做出改变。”
“爆炸原理”(principle of explosion)更有意思,也就是人们所说的“从矛盾中可以推导出任何命题”。
假设你相信P:赫克斯泰布尔在英国。再假设你相信非P:赫克斯泰布尔不在英国。通过析取加法,你可以从P推导出“P或Q”:赫克斯泰布尔在英国,或者独角兽存在。然后,通过析取三段论,你可以从“P或Q”和“非P”推导出Q:“赫克斯泰布尔不在英国。因此,独角兽存在。”恭喜你!你刚刚从逻辑上证明了独角兽的存在。人们经常错误地引用拉尔夫·沃尔多·爱默生(Ralph Waldo Emerson)的话:“僵化地坚持一致性是愚蠢的。”事实上,他说的是那种愚蠢的一致性,他认为“伟大的灵魂”要超越这种一致性。不过,无论是哪种情况,这种说法都未必可信。
 如果你的信仰体系中有矛盾,你可以相信任何事情。摩根贝瑟曾经这样评价一个他不喜欢的哲学家:“那个家伙有P和非P两个断言,然后推导出了一切。”
如果你的信仰体系中有矛盾,你可以相信任何事情。摩根贝瑟曾经这样评价一个他不喜欢的哲学家:“那个家伙有P和非P两个断言,然后推导出了一切。”

有效的推理规则也可能得出荒谬的结论,这是逻辑论证的一个特点。把推理规则正确地应用于前提的论证,我们称之为有效论证(valid argument)。有效论证只是告诉我们:如果前提为真,那么结论一定为真。它不保证前提为真,因此对结论的真实性也无法下定论。这与可靠论证(sound argument)形成了鲜明对比,可靠论证是将规则正确地应用于真前提,从而得出真结论。下面这个论证是有效的:“如果希拉里·克林顿赢得2016年美国总统大选,那么2017年蒂姆·凯恩(Tim Kaine)就任美国副总统。希拉里·克林顿赢得了2016年美国总统大选。因此,2017年蒂姆·凯恩就任美国副总统。”但这不是一个可靠论证,因为希拉里实际上并没有赢得2016年的大选。“如果唐纳德·特朗普赢得2016年美国总统大选,那么2017年迈克·彭斯(Mike Pence)就任为美国副总统。唐纳德·特朗普赢得了2016年大选。因此,2017年,迈克·彭斯就任副总统。”这个论证既有效又可靠。
将有效论证呈现为可靠论证,是一个常见谬误。一位政客承诺:“如果我们消除官僚机构的浪费和欺诈行为,就可以降低政府税收、增加居民收入,并且实现预算平衡。我要杜绝浪费和欺诈。所以,投我一票吧,一切都会好起来的。”幸好人们经常能发现不可靠的地方,对于从可疑前提推出似是而非结论的诡辩家,人们可以做出各种各样的反驳:“那简直是痴人说梦”“愿望不等于事实”“假设有一头球形的奶牛”
 。我最喜欢的一个说法来自意第绪语
。我最喜欢的一个说法来自意第绪语
 :“如果我祖母有‘蛋蛋’,她就会是我祖父。”
:“如果我祖母有‘蛋蛋’,她就会是我祖父。”
实际上,许多推断甚至是无效的。古典逻辑学家也收集各种各样的无效推断或形式谬误。在这些陈述句序列中,结论似乎是根据前提得出的,但实际上并非如此。其中最有名的是“肯定后件”(affirming the consequent):“如果P,那么Q;Q为真;所以P为真。”如果下雨了,那么道路就是湿的。道路是湿的,所以下雨了。这一论证不是有效的,因为一辆洒水车可能刚刚经过。一个类似的谬误是“否定前件”(denying the antecedent):“如果P,那么Q;非P;所以非Q。”没有下雨,所以,街道不是湿的。这一论证同样也是无效的。换一种说法就是,“如果P,那么Q”这个陈述成立,并不意味着它的逆命题“如果Q,那么P”也成立,也不意味着它的否命题“如果非P,那么非Q”成立。
不过,人们是倾向于“肯定后件”的,即把“P蕴含Q”和“Q蕴含P”二者混淆起来。这就是为什么在沃森选择任务中,许多被要求验证“如果D,那么3”的人会翻3那张卡片。这就是为什么美国保守派政客鼓动选民从“如果某人是社会主义者,那么他可能是民主党人”这样的推断转向“如果某人是民主党人,那么他可能是社会主义者”。正因为如此,蠢材喜欢说,历史上所有伟大的天才都曾在他们生活的年代被人嘲笑过,但他们忘记了“如果是天才,那么被人嘲笑”这个命题并不意味着“如果被人嘲笑,那么是天才”。懒惰的人应该记住这一点,因为他们中有人声称最成功的科技公司都是由从大学退学的人创立的。
好在我们经常能发现这种谬误。欧文是一个疑病症患者,他跟医生说:“我确信我患了肝病。”“那是不可能的,”医生回答,“如果你有肝病,你是无法知道的,因为这种病不会让你表现出任何不适。”欧文回答说:“没有任何不适正是我的症状!”
顺便说一下,如果你特别留意我所举过的例子,你会注意到,我举例的那些P和Q的表达并不总是一致的;如果逻辑的本质就是操纵符号,那么我就本应该让P和Q的表达保持一致。相反,我会对主语、时态、数值和助动词做些改变。“某个人是女人”变成了“赞西佩是女人”;“你邀请”和“奥利弗邀请”交替出现;“你必须戴头盔”调换为“这个孩子戴着头盔”。这些编辑工作很重要:在特定语境下,“你必须戴头盔”与“一个没戴头盔的孩子”并不矛盾。逻辑学家因此而创造了更强大的逻辑系统,将命题演算中的P和Q拆分成了更小的部分。更强大的逻辑系统包括:谓词演算,区分了主词和谓词,以及所有和存在;模态逻辑,区分“巴黎是法国的首都”这类偶然为真的陈述和“2+2=4”这类必然为真的陈述;时序逻辑,区分过去、现在和未来;道义逻辑,研究允许、义务和责任。
