




在指定的下降方式和飞机起始状态条件下,可用最优下降性能数据中插值获得燃油消耗量最小时的最优下降表速、下降顶点位置及最优下滑角等参数。最优下降性能数据计算示意如图2-3所示。
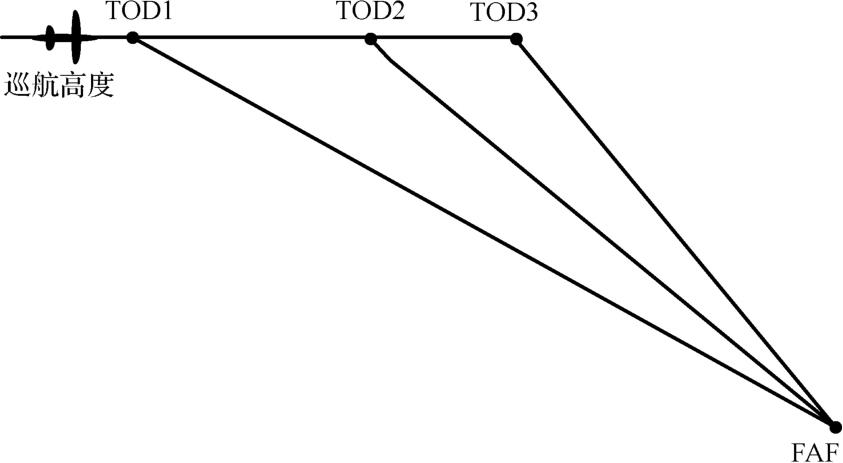
图2-3 最优下降性能数据计算示意
给定下降方式后,对飞机在下降过程中的燃油消耗量随下降表速的变化关系进行函数拟合,找到每一高度下拟合函数的极值点,该极值点对应的速度即从指定高度下降的最优下降速度;从2.3节计算得到的基本下降性能数据中插值得到下降水平距离,并将该下降水平距离作为指定高度下的下降顶点(TOD)到最后进近定位点(FAF)的水平距离,从而确定不同高度下燃油消耗量最小时的下降顶点位置。最优下降性能数据计算流程图如图2-4所示。
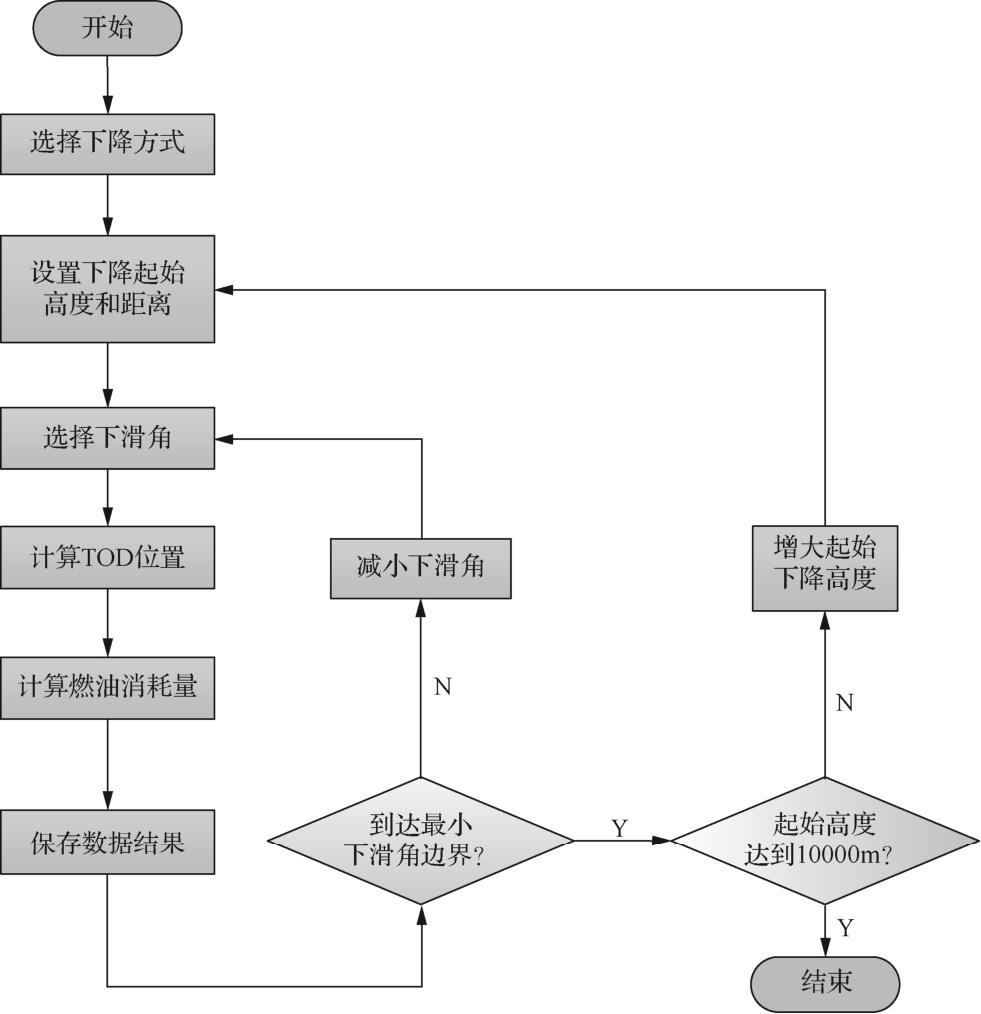
图2-4 最优下降性能数据计算流程图
例如,选择的下降方式为等表速下降,超始高度为4000m,最后进近定位点的高度为500m,分别以不同的下降表速进行等表速下降仿真,计算结果见表2-10。
表2-10 不同下降表速下燃油消耗量计算结果

为了得到燃油消耗量随下降表速的变化关系,分别用二次多项式 y = a 2 x 2 + a 1 x + a 0 和三次多项式 y = a 3 x 3 + a 2 x 2 + a 1 x + a 0 对表2-10中的数据进行拟合,得到如图2-5所示的曲线。拟合函数中的 x 代表燃油消耗量,单位为kg; y 代表下降表速,单位为m/s。拟合结果见表2-11。
表2-11 燃油消耗量随下降表速变化的拟合结果

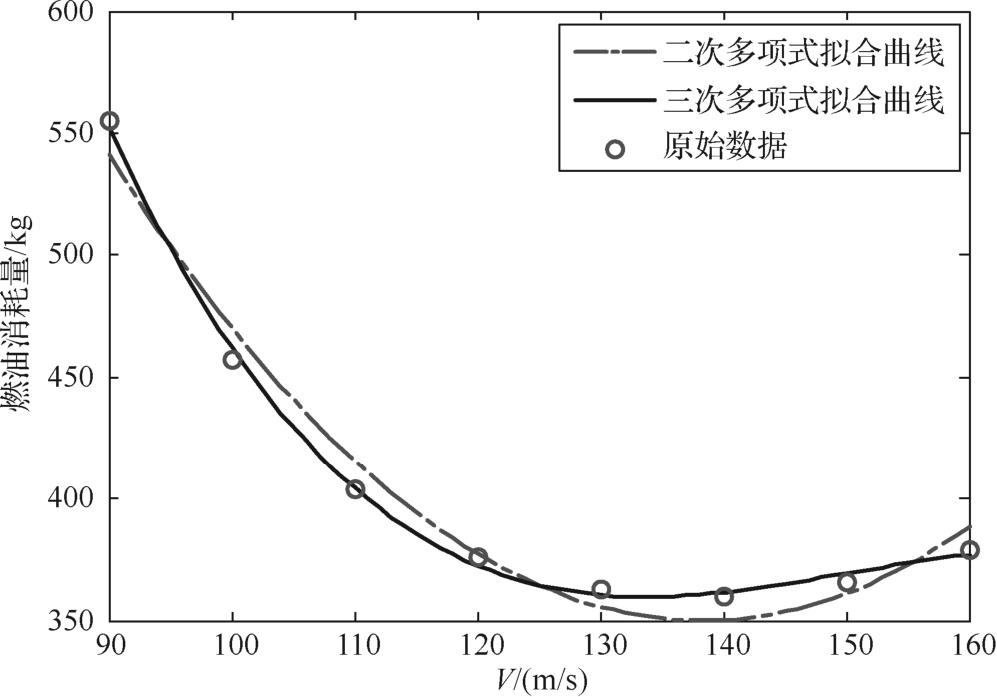
图2-5 燃油消耗量随下降表速变化的拟合结果
从图2-5可以看出,二次多项式拟合结果的残差较大,而采用三次多项式拟合结果的残差较小,因此,选择三次多项式进行拟合。图2-5表明,在指定下降起始高度下,以大约130m/s的下降表速进行等表速下降,对应的燃油消耗量最小;低于此表速时,由于下降表速较小,增加了下降飞行时间的同时也增大了燃油消耗量;高于此表速时,为了维持较大的下降表速,需要增大单位时间内的燃油消耗量,进而增大发动机推力,也会增大燃油消耗量。
由此可知,最优下降表速为130m/s,根据2.3节的计算结果,可知对应的下降水平距离为59km。因此。该高度下的最优下滑角可以通过式(2-10)计算:

式中, γ 为对应高度下的最优下滑角;Δ h 为起始下降高度, s 为下降水平距离。
用同样的方法对从其他高度下的下降表速和燃油消耗量变化关系进行函数拟合,基于2.3节中的基本下降性能计算结果,插值计算出对应的下降水平距离,可得到不同高度下燃油消耗量最小时的最优下降表速、下降顶点位置和最优下滑角,具体见表2-12。
表2-12 不同高度下燃油消耗量最小的最优下降性能数据
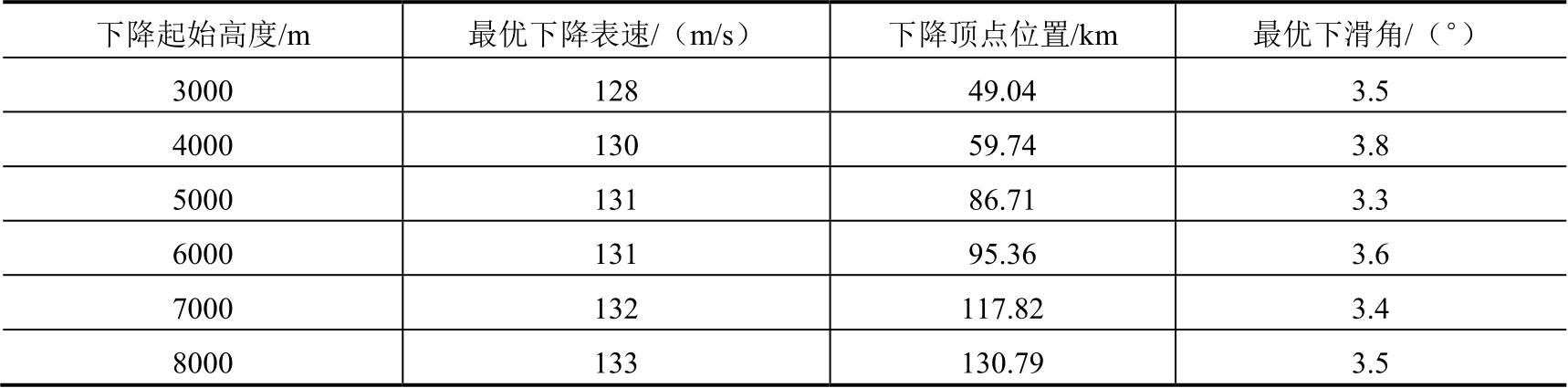
其他下降方式(等马赫数下降、先等马赫数再等表速下降)下最优下降性能数据库的建立方法与此相同,不再赘述。由此可知,根据所建立的最优下降性能数据库,只须选择下降方式、下降起始高度和最优性能指标(燃油消耗量最小、下降水平距离最短、下降飞行时间最少),便可得到对应高度下的最优下滑角和下降顶点位置。