




刚体的转动定律是刚体转动的动力学规律,与牛顿第二定律 F = ma 相对应,作用力 F 对应为作用力矩 M ,加速度 α 对应为角加速度 β ,而质量 m 则对应为刚体的转动惯量 I ,即 M = Iβ 。刚体转动定律及刚体转动惯量的研究,对于物体转动规律、机器设计及制造有着非常重要的实际意义。物体的转动惯量大小取决于物体的形状、质量分布和转轴的位置。几何形状简单的匀质刚体绕特定轴的转动惯量可由公式直接计算,而形状复杂或非匀质刚体的转动惯量则必须用实验方法进行测定。因此,学习刚体转动惯量的测定方法,具有重要的实际意义。
1.验证刚体转动定律,测定刚体的转动惯量。
2.观测转动惯量与质量分布的关系。
刚体转动实验仪、秒表、米尺、游标卡尺、物理天平、砝码等。
刚体转动实验装置如图2-1所示。图中A是一个具有不同半径 r 的塔轮,可使相同绳张力作用产生不同的外力矩。塔轮两边对称地伸出两根有等分刻度的均匀细杆B和B',B和B'上各有一个可以移动的圆柱形重物 m 0 ,用以观测转动惯量随质量分布的变化规律以及验证平行轴定理。它们一起组成一个可绕固定轴OO'转动的刚体系。塔轮上绕一细绳,通过滑轮C与砝码 m 相连,当砝码下落时通过细绳对刚体施加外力矩。滑轮C的支架可以借固定螺丝D而升降,以保证细绳绕塔轮不同的半径转动时均可保持与转轴相垂直。滑轮台架E上有一个标识F用来判断砝码m的起始位置。H是有固定台架的螺旋扳手。取下塔轮,换上铅直准钉,通过底脚螺丝S 1 、S 2 、S 3 可以调节OO'竖直。调好OO'轴线竖直后,再装上塔轮,转动合适后用固定螺丝G固定。
当塔轮和横杆系统组成的体系在重物 m 的重力作用下绕固定转轴转动时,根据转动定律,有

式中: M 为刚体所受的合外力矩(主要由细绳的张力矩 T · r 和轴承的摩擦力矩M f 构成),即 M = T · r - M f ; I 为刚体对该轴的转动惯量; β 为角加速度。
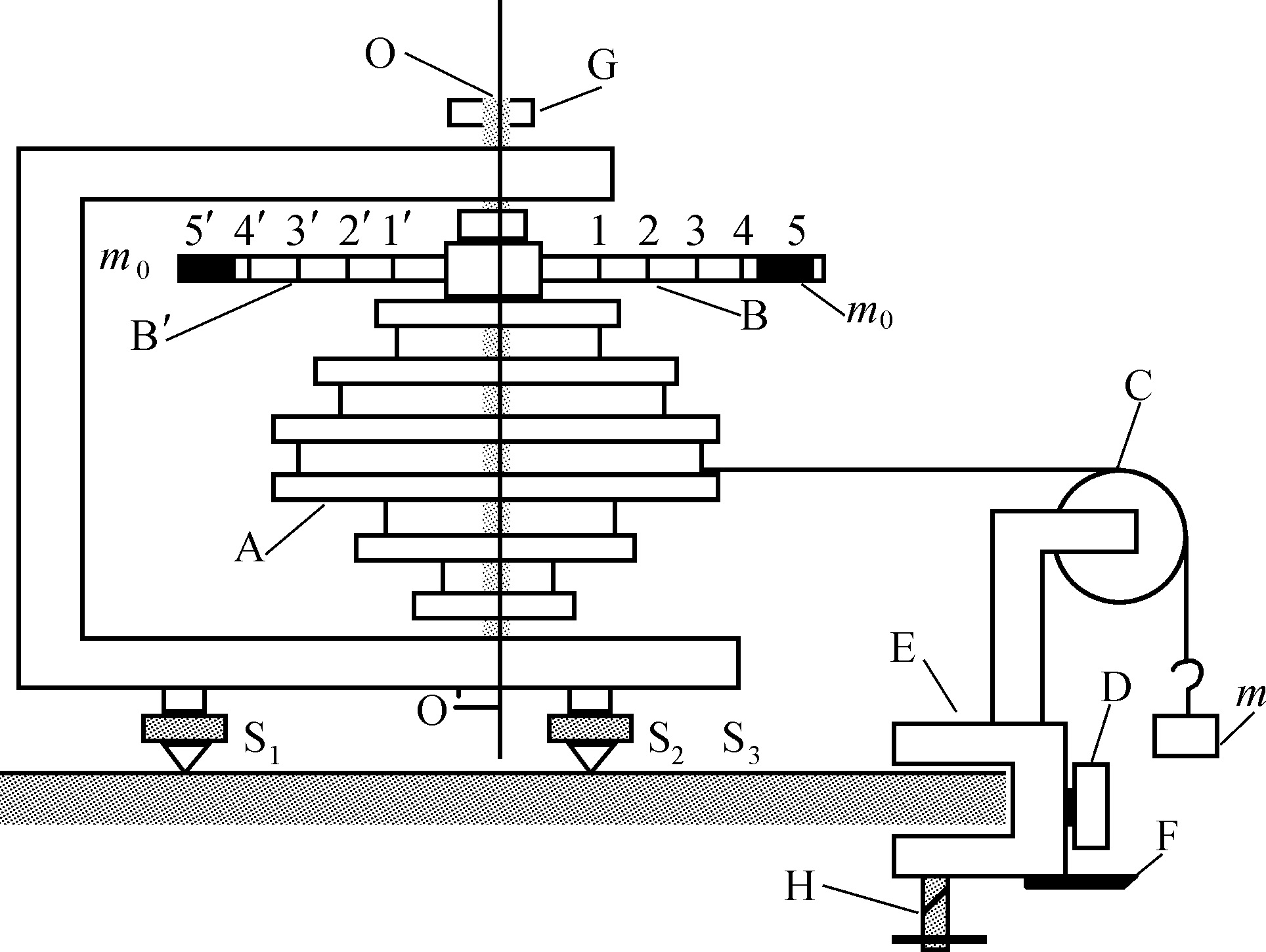
图2-1 刚体转动惯量实验仪
设细绳的张力为T,砝码 m 以匀加速度 a 从静止开始下落,下落的高度为 h ,所需时间为 t ,若忽略滑轮及细绳的质量以及滑轮上的摩擦力,且绳不伸长,则有

由式(2-1)、式(2-2)可得

实验中若保持 g ≫ a ,则式(2-3)变为

若保持 r 、 h 及重物 m 0 的位置不变,改变砝码 m 的大小,则相应的下落时间 t 发生改变,则由式(2-4)有
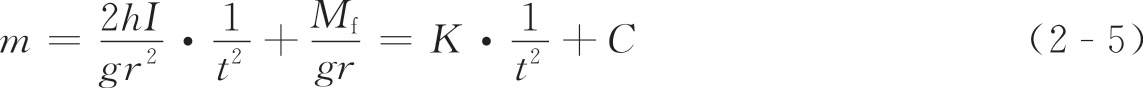
式中:
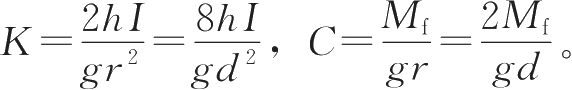
上式表明,
m
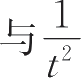 呈线性关系。
呈线性关系。
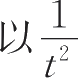 为横坐标,
m
为纵坐标,做
为横坐标,
m
为纵坐标,做
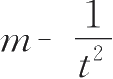 图线,则得一直线,由直线的斜率
K
和截距
C
即可求出刚体的转动惯量
I
摩擦力矩
M
f
。
图线,则得一直线,由直线的斜率
K
和截距
C
即可求出刚体的转动惯量
I
摩擦力矩
M
f
。
1.按图2-1把仪器安放在实验桌上,取下塔轮,换上铅垂准钉,调节水平螺丝,使OO'轴铅直,再装上塔轮,调节塔轮轴上的固定螺丝使塔轮转动灵活,尽量减少摩擦。调好后用固定螺丝固定,绕线尽量密排。
2.把细绳密绕在半径 r 的塔轮上(建议绕在半径最大的塔轮上),另一端线通过滑轮C系住砝码。调节滑轮C的高度,保持细绳与塔轮转轴相垂直,两个重物 m 0 分别放在细杆B、B'的5、5'位置。取塔轮和细杆B、B'及两个重物 m 0 为转动刚体。
3.将砝码(质量为5.00g)放置在标记F处静止,然后让其自由下落到某一固定位置(一般使其下落到地面为止),保持 h 不变,用秒表测出通过这段距离 h 所需的时间 t 。重复测5次,取 t 的平均值。
4.然后改变 m 值,至少6次,每次增加5.00g砝码,用同样的方法测出相应 m i 值、下落的时间 t i 。记录在表2-2中。
5.做出
m
-
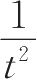 图,验证刚体转动定律,并由直线斜率
K
=
图,验证刚体转动定律,并由直线斜率
K
=
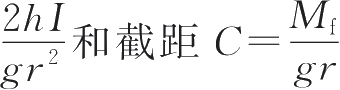 求出刚体的转动惯量
I
和摩擦力矩
M
f
。
求出刚体的转动惯量
I
和摩擦力矩
M
f
。
6.改变细棒上 m 0 的位置,观测刚体转动惯量随其分布不同而改变的状况。
7.实验完毕后,将仪器整理好,恢复原位,由教师验收。
表2-1

表2-2
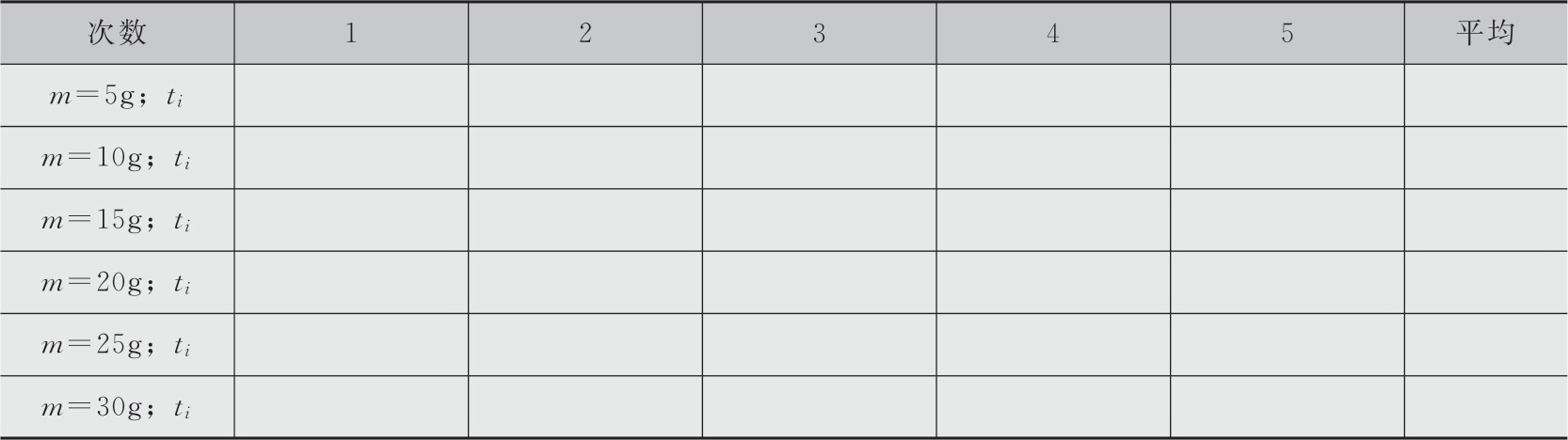
表2-3

做出m-
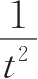 图,验证刚体转动定律,并由直线斜率
K
=
图,验证刚体转动定律,并由直线斜率
K
=
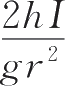 和截距
C
=
和截距
C
=
 求出刚体的转动惯量
I
和摩擦力矩
M
f
。
求出刚体的转动惯量
I
和摩擦力矩
M
f
。
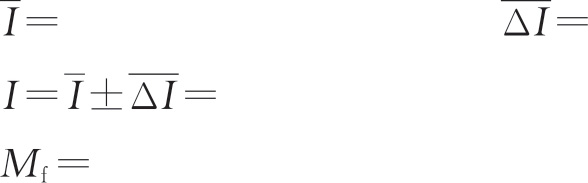
1.实验中配备了10个砝码,每个砝码的质量均为5g。
2.细线要与塔轮相切。
3.细线要与桌面相平行(或细线要与OO'轴垂直)。
1.误差产生的主要原因是什么?在做实验时应注意什么?
2.写出用误差传递公式计算转动惯量 I 的绝对误差Δ I 的计算过程。(提示:将 I 看成 d 和 h 的函数,把 K 作为真值看待)。