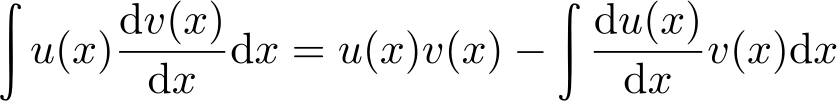在有限维系统状态空间中,向量范数是等价的。因此,在不同向量范数意义下的指数稳定定义也是等价的。而对于无限维系统,在泛函空间中范数是不等价的,因此其指数稳定定义缺乏一般性。因此,本节给出DPS在‖·‖ 2 范数意义下的指数稳定性定义。在介绍稳定性的相关概念之前,考虑一个简单抛物型DPS,其系统模型如下:
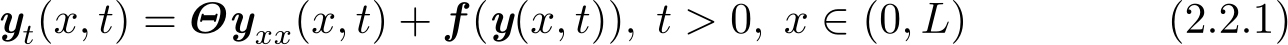
受限于纽曼边界条件
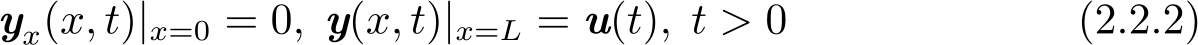
和初始条件

式中, y (·, t )∈ H n ([0, L ])和 u ( t )∈ℜ n 分别表示状态和边界控制输入; x ∈[0, L ]⊂ℜ和 t ∈[0,∞)分别表示空间和时间;0< Θ ∈ℜ n × n 是给定的常数矩阵; f ( y ( x , t ))是关于 y ( x , t )连续可微的非线性函数且满足 f (0)=0; y 0 ( x )是初值。
以下定义给出了当 u ( t )=0时,半线性抛物型DPS(2.2.1)~(2.2.3)在‖·‖ 2 范数意义下的指数稳定性定义。
定义2.2 [85] 当 u ( t )=0时,若存在两个常数 δ 1 ≥1和 ρ 1 ≥0,使得
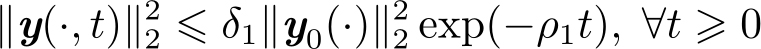
成立,则称系统(2.2.1)~(2.2.3)是指数稳定的。
定义2.3 [85] 当 u ( t )=0时,若存在常数 δ 2 ≥1, ρ 2 ≥0及 κ 1 >0, κ 2 >0,使得
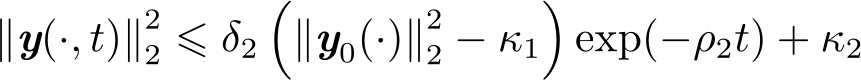
成立,则称系统(2.2.1)~(2.2.3)是实用指数稳定的。
定理2.1 (Lyapunov直接法-指数稳定性定理) 设 y (·, t )∈ D 为系统(2.2.1)~(2.2.3)的状态向量( D 是定义在 H 2 ([0, L ])上包含平衡态 y (·, t )=0的一个开子集)。对于∀ y (·, t )∈ D ,设连续可微函数 V ( t )≥0及其导数满足
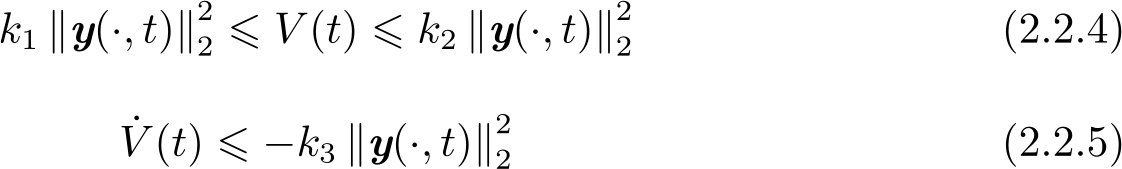
式中,若 k 1 、 k 2 、 k 3 为正常数,则称系统(2.2.1)~(2.2.3)是指数稳定的。
证明:根据式(2.2.4)和式(2.2.5),可知 V ( t )满足微分不等式
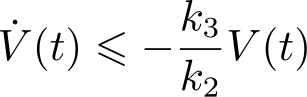
进一步得
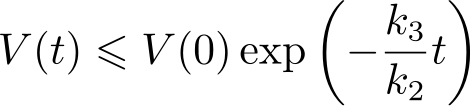
由式(2.2.4)可得
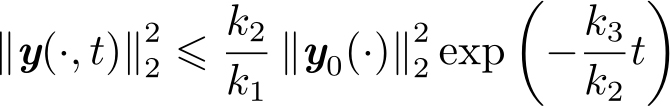
因此,系统(2.2.1)~(2.2.3)是指数稳定的。
定理2.2 (Lyapunov直接法-实用指数稳定性定理) 设 y (·, t )∈ D 为系统(2.2.1)~(2.2.3)的状态向量( D 是定义在 H 2 ([0, L ])上包含平衡态 y (·, t )=0的一个开子集)。对于∀ y (·, t )∈ D ,设连续可微函数 V ( t )≥0及其导数满足
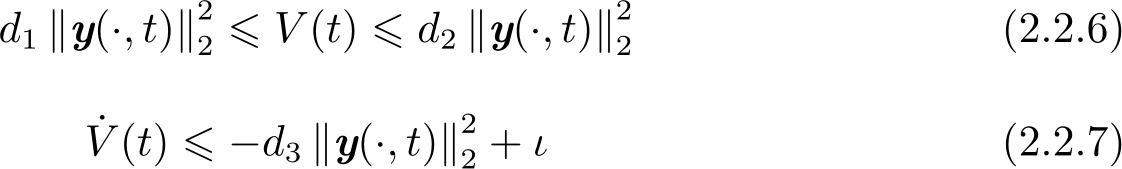
式中,若 d 1 、 d 2 、 d 3 为正常数,则称系统(2.2.1)~(2.2.3)是实用指数稳定的。
证明:根据式(2.2.6)和式(2.2.7),可知 V ( t )满足微分不等式
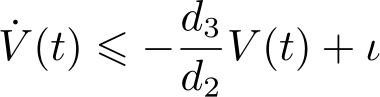
进一步得
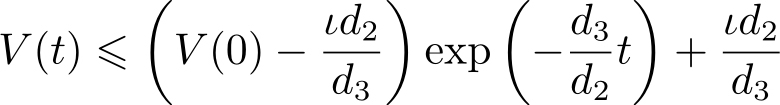
由式(2.2.6)可得
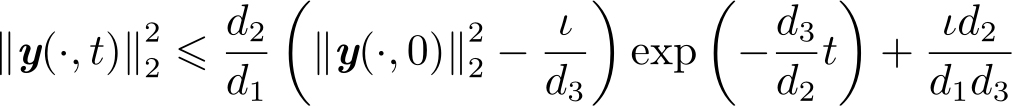
因此,系统(2.2.1)~(2.2.3)是实用指数稳定的。
在后面章节探讨基于Lyapunov直接法的DPS稳定性分析时还将用到分部积分技术。
定理2.3
(分部积分技术)
[124]
设
u
=
u
(
x
)和
v
=
v
(
x
)是两个关于
x
的函数,各自有连续导数
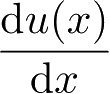 和
和
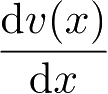 且
且
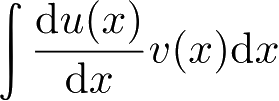 存在,根据函数乘积求微分法则,
存在,根据函数乘积求微分法则,
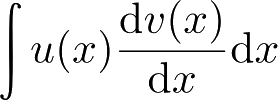 存在,那么可得分部积分技术公式为
存在,那么可得分部积分技术公式为