




定义2.1 关系式中包含多元未知函数及其偏导数的方程称为偏微分方程。
考虑到二阶偏微分方程在数学、物理及工程技术中的广泛应用,接下来着重介绍二阶偏微分方程。根据空间微分算子的性质,二阶偏微分方程可分为双曲型、抛物型和椭圆型三类 [24] 。二阶二元线性偏微分方程及其特征方程 [74] 形式为
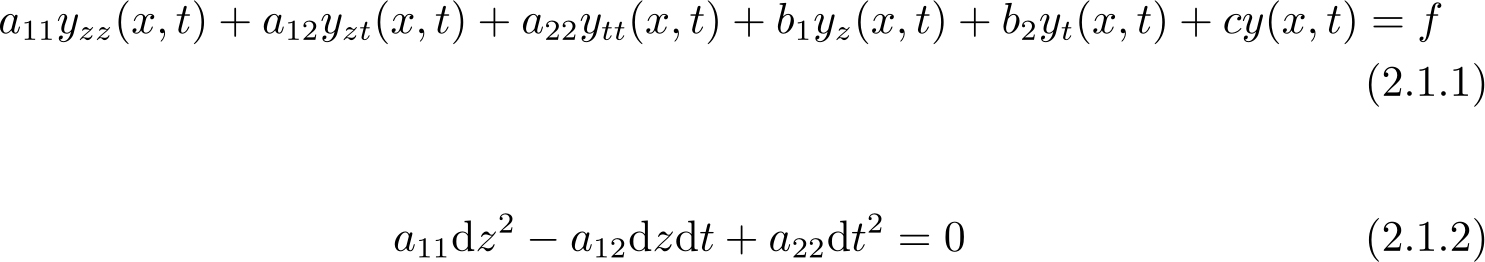
式中,
a
11
、
a
12
、
a
22
、
b
1
、
b
2
、
c
与
f
是关于自变量
x
和
t
的函数,方程(2.1.1)在平面(
x
,
t
)上的某一子区域上是连续可微的,且在点
Z
(
x
0
,
t
0
)的邻域内可以根据
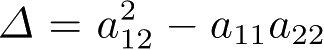 的符号分为三类:
Δ
>0,方程(2.1.1)在点
Z
处为双曲型偏微分方程;
Δ
=0与
Δ
<0分别称为抛物型和椭圆型偏微分方程。为保证其解析解的存在性和唯一性,偏微分方程(2.1.1)不仅受限于初始条件,还受限于边界条件。
的符号分为三类:
Δ
>0,方程(2.1.1)在点
Z
处为双曲型偏微分方程;
Δ
=0与
Δ
<0分别称为抛物型和椭圆型偏微分方程。为保证其解析解的存在性和唯一性,偏微分方程(2.1.1)不仅受限于初始条件,还受限于边界条件。
以一维空间( x ∈[0, L ])为例,偏微分方程的边界条件可分为狄利克雷(Dirichlet)、纽曼(Neumann)和混合(Robin)三类。具体而言,针对二阶偏微分方程
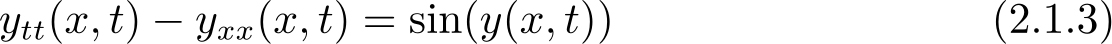
其边界条件通常有以下三种类型。
第一类狄利克雷边界条件:
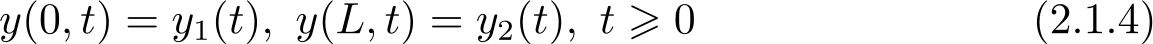
式中,函数 y 1 ( t )和 y 2 ( t )分别表示状态 y ( x , t )在边界 x =0与 x = L 处的运动规律。
第二类纽曼边界条件:
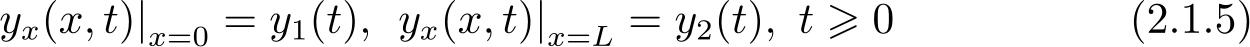
式中,函数 y 1 ( t )和 y 2 ( t )分别表示状态 y ( x , t )在边界 x =0与 x = L 处外法线方向导数的运动规律。
第三类混合边界条件:
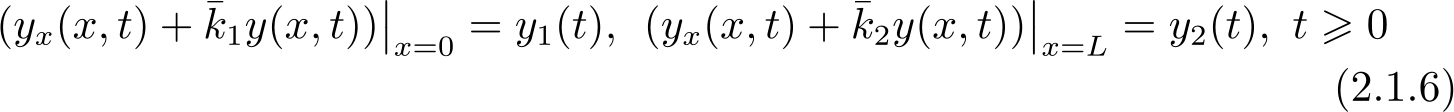
式中,函数
y
1
(
t
)和
y
2
(
t
)分别表示在边界
x
=0和
x
=
L
处状态
y
(
x
,
t
)和其外法线方向导数线性组合的运动规律;
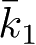 与
与
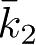 为已知函数。
为已知函数。
在上述三类边界条件中,若令 y 1 ( t )=0且 y 2 ( t )=0,则称上述边界条件为齐次边界条件,否则称为非齐次边界条件。