




并不是所有图形都像圆一样好画。有了圆规,我们可以快速地画出一两个圆,但要画一个五边形,就不那么容易了。用直尺画一个五边形倒是很容易,但如果想要画一个5条边都相等的正五边形(regular pentagon),你会发现很容易将它画成梨形。众所周知,几何起源于古希腊。那时的人们就非常钟爱正五边形,如果能画出一个正五边形,你甚至可以加入一些秘密的数学俱乐部。当然,我没办法保证你也能加入,但是我可以教大家小小地做一下弊。
拿出一条长纸带,打一个简单的纸结,慢慢拉紧并小心地压平。最终,这个纸结就会变成一个正五边形。不信的话,你可以用尺子量量每边的长度。如果你仍然不信,可以阅读书后“疑难解答”中我对这五条边边长相等的理论证明。用这个方法,你可以在任何场合用非常短的时间得到正五边形,它也因此得到了“应急五边形”(emergency pentagon)的称号。
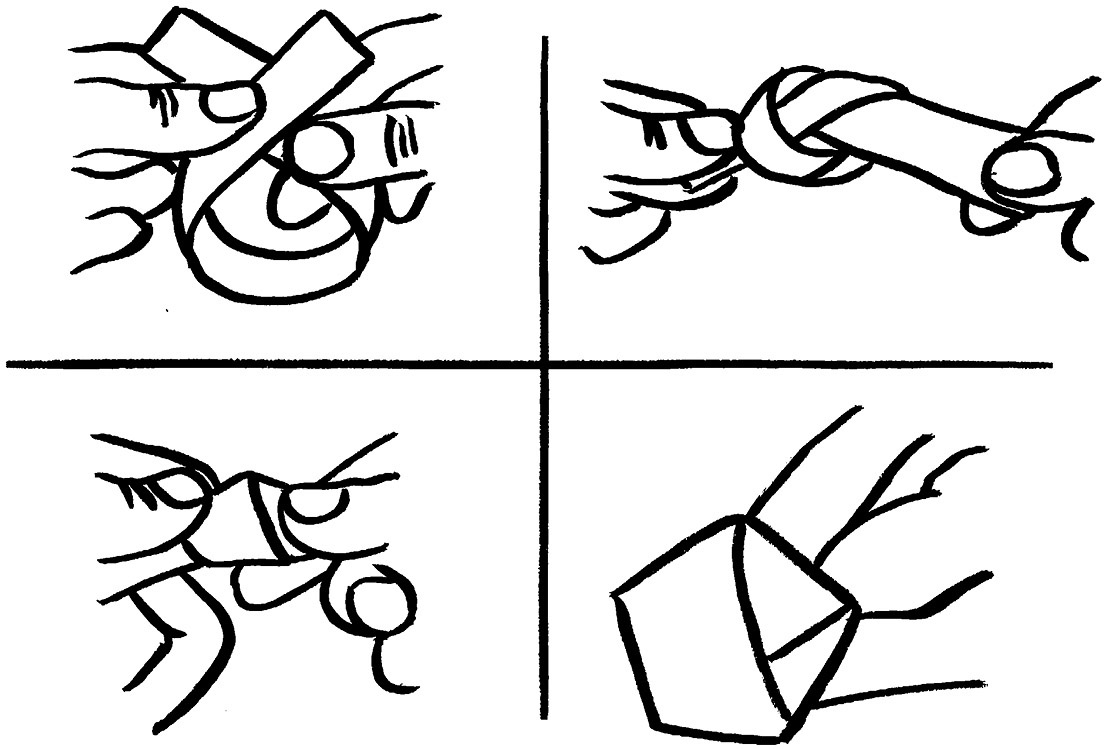
用纸带打结,折出正五边形
不过,这个“应急五边形”并不能让你得到加入古希腊秘密数学俱乐部的许可(并且在大多数紧急情况下没什么用)。在公元前300年左右,古希腊人沉迷于用圆规和直尺构建图形。直到如今,人们依然被古希腊人及他们构建图形的方法深深吸引,因为最早的一批数学家就在那时产生,并且几何也是数学的第一个分支领域。因此,我们有充足的理由认为,直尺和圆规是数学的起源。这也说明,为什么数从来都不曾成为“真正的数学”。
但毫无疑问,计数比画图更古老,数的出现确实早于几何。有证据显示,数的使用可以追溯到史前时期,那时人们常常在湿黏土上刻画记号,用以计数。一些远古黏土板留存至今,上面常常记录着金钱交易、追踪家畜数目、预测潮汐随月亮的运动规律等。也有一些黏土板上刻有我们认为是“练习”的内容,这些练习是一些传授重要算数技能的谜题,人们学会这些算数技能后可将其应用于实际。这些练习看起来很像是数学,但缺少两个重要属性:第一,没有人能够严格证明他们所运用的数学理论确实是正确的;第二,他们学习这些技能不是为了好玩。
人们最初使用几何的时候,确实是出于实际目的,比如划分田地或者建造房屋。形状仅仅是辅助计数的工具,用以提升社会文明,但到了古希腊时期,这种情况发生了改变。古希腊人开始追求纯粹的数学本身。在他们看来,数学是一种游戏。不仅如此,他们不仅仅想找到问题的答案,更想证明答案百分百可信,即的的确确是问题的解。这种全新的数学研究方式被一个人发挥到极致,他就是欧几里得(Euclid)。
欧几里得出生于公元前300年左右(古希腊人的一个不按常理出牌的方式是不记录出生日期),不过据我们所知,“欧几里得”可能是一个团体的笔名。但毋庸置疑,他(们)编写的13本著作流传至今,其中最有名的一本莫过于《几何原本》。他(们)试图在书中囊括当时人们掌握的全部数学知识, 并 严格证明它们的正确性。
欧几里得不希望人们完全相信他(们),或者信奉任何事物。他们认为每一步都必须经过严格的证明。但遗憾的是,我们不可能凭空证明 每一件事 ,你必须从一些公认正确的事实开始,然后看看可以从这些假设证明出什么。因此,欧几里得选了一些最显而易见的事实作为公理,假设它们是正确的,并且无须证明。其中主要的两条公理是:可以用直尺画出一条直线;可以用圆规画出一个圆。你绝对不会想到这两个东西能帮助你证明多少东西!
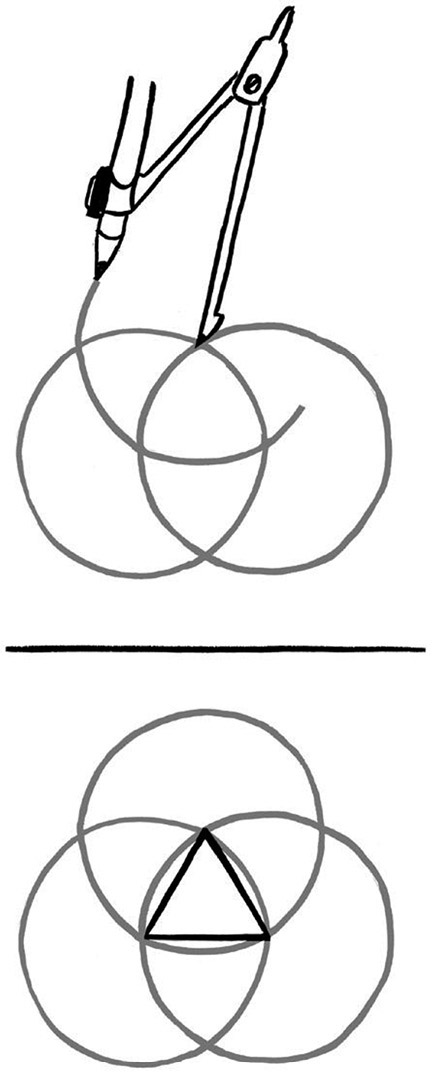
画3个圆,你就能得到一个正三角形
现在我们可以动手试试。首先,试试你能否用直尺和圆规(以下简称尺规)画出一个3条边都相等的三角形,即等边三角形(equilateral triangle),也叫正三角形(regular triangle)。如果你觉得太简单,那就再试试画一个正方形(显然,它的4条边长度都相等),或者正六边形(regular hexagon)。但当你尝试画五边形时,真的挑战才终于开始了。这些实验显示,你不需要事先假定三角形存在。《几何原本》中的第一条证明就是如何用尺规画出正三角形。一旦你接受了直线与圆的存在,那么正三角形、正方形、正五边形、正六边形的存在将是很自然的结论。
与数的抽象类似,这是另一种抽象的实例。我们了解的数学始于人们将图形从物理现实中剥离出来,并试图以抽象的方式去理解它们。直角就是从田间两根篱笆的交角抽象出来的概念。形状不像数那样受限于计数系统。在几何中,无论我们如何表达,圆就是圆,直线就是直线。那些假设存在的外星人会与我们争执怎样写一个数,但他一定会认同,五边形就是五边形(无论以什么语言。所以我们会继续使用几何语言——尺规来表达图形)。

在直线上画些圆弧,你就能得到一个正方形
然而有趣的是,外星人的证明可能起源于和希腊人不同的假设。用纸条折出正五边形在欧氏几何看来并不算是合理的作图方法,因为它超出了最开始的两条假设,但我们的天外来客可能会觉得无所谓。人类向来热衷于画图,因此,我们对图形的理解在很大程度上依赖于画的过程,但外星人朋友或许更爱折纸,对折纸的几何学有更深的了解。事实上,图形中的问题比欧几里得想象的更多。