下载掌阅APP，畅读海量书库
立即打开
你能在10和20之间找到不能用连续数（consecutive number）之和表示的数吗？这个问题的答案只有一个。
肯定不是13，因为13=6+7，而6和7是连续数；类似地，18也可以排除，因为18=5+6+7。如果你找到了答案，可以继续在30和40之间寻找。再找到下一个数，它刚好超过60。现在，你应该能发现其中的规律。有趣的是，不管你怎么表达数，“连续数之和”这个问题总是有效的。古罗马人用他们自己的数字可以解答这个问题，古玛雅人也可以解，假如真的有外星人，他们也可以解。
你发现的第一个答案应该是16：连续数的和不能为16。16是这类数字组合中的一员，其他的还有8和32（你可以在本书后面的“疑难解答”中找到这些数字为什么有这种特性）。
如果你想知道有没有在一种特定的计数系统中产生的难题，在另一种计数系统中却不成立，那就让我们回到累进可除数，把所有的非零数字各使用一次，但是用另一个基数不是10的计数系统吧。（如果你得回翻几页书才能想起来什么是累进可除数，别气馁，因为我写到这里的时候也忘了它是什么了。）如果人类演化成另一个模样，使用四进制计数，那么当我躺在牙医的椅子上时，我就能得到两个答案：123和321。五进制下没有解；六进制下又有两个答案（14,325和54,321）；七进制下也没有解；八进制下有惊人的3个解（3,254,167、5,234,761和5,674,321）；九进制下没有解；十进制下我们已经知道只有一个解（381,654,729）；最后一个解是十四进制数：9C3A5476B812D。呼，终于列完了。
我很惊讶十二进制居然没有解。如果我们的天外来客真的使用十二进制（虽然我不知道你是否了解他们，但我觉得人类对他们越来越熟悉了），这个难题将对他们彻底失效。（又找到了一个反对十二进制拥护者的新理由！）我之前写程序寻找这样的数时（花了一个闲暇的周末），十四进制解的突然出现让我非常惊讶：我曾经认为，如果十二进制没有解，那更高的进制也应该没有解。接着我尽可能地对程序进行了优化，让它继续在十五进制、十六进制中寻找答案，但最终没有找到。我不知道十六进制以上有没有解。如果你的时间比我更充裕或者有更高超的编程能力，找到答案后记得告诉我。
把问题放在不同情形下探索，看看会发生什么的行为叫作推广（generalizing），正是这一做法驱使着数学向前发展。数学家总想寻找适用于最多情形的解和规律。在找到一道数学难题的一个解后，事情还远没有结束，你还需要将其推广到尽可能多的情形。在这方面，莱昂哈德·欧拉（Leonhard Euler，瑞士著名数学家、物理学家）和开尔文勋爵（Lord Kelvin，英国著名物理学家、数学家）这样的数学家通过展现这样的好奇心，取得了异于常人的数学成就。相比那些与数字符号及我们使用的进制相关的难题，数学家更喜欢那些纯粹触及数自身性质的难题，那些只在某一进制下才有效的问题总是被当作次品。数学家不喜欢只在十进制中有效的问题，只因为我们有10根手指，他们才对这个计数系统感兴趣。数学探寻的是普适真理，而不是某种计数系统下的特例。
虽说如此，还是有一些只在十进制下成立的数字难题，它们的意义却非常重大。但你别跟英国伟大的数学家G. H.哈代（G. H. Hardy）聊这个。他于1940年指出了一个有趣的事实：在1之后，只有4个数可以表示成该数中所有数字的立方之和。之后，他又认为“这里面没有什么吸引数学家的东西”，所以将其搁置一边。他认为这样的数字难题“更适合放在谜题专栏来娱乐业余爱好者”，数学应该和这些娱乐用谜题划清界限。但不好意思的是，我个人却很喜欢这些无意义的数。
这4个数分别是：
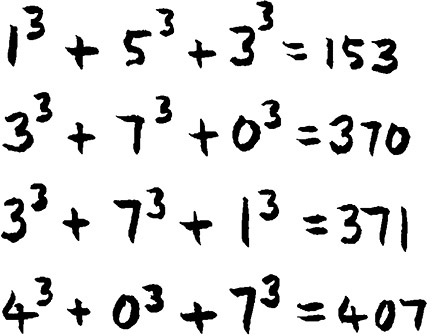
除了1 3 =1，再没有其他数符合这个等式了，但是没多久，人们便开始推广它们，虽然还是在十进制之下。（所以哈代的声明没能让人放弃解答这个问题。）人们注意到这仅有的4个数居然都是三位数，所以开始寻找能表示成为各数字四次方之和的四位数。（结果有3个数，8,208是其中之一。）因为这些数看起来很“自恋”，总会“审视”自己有多少个数字，所以它们被称为自恋数（narcissistic number）。如果你对此感兴趣，我还可以告诉你54,748是3个五位自恋数之一，而在五位数之外还有很多自恋数。借助于计算机的超强计算能力，你可以找到最大的自恋数。它是一个由39位数字组成的怪物：115,132,219,018,763,992,565,095,597,973,971,522,401。
别再深入下去了，这一点都不好玩。哦，好吧，我再补充几点。不存在两位自恋数：没有哪个两位数可以表示成为各数字的平方和，我确实验证过。所有一位数都是自恋数，因为它们的一次方就是自身，所以它们被称为平凡自恋数。在数学语言中，“平凡”就是“无趣”的意思，也就是说虽然符合条件，但结果很无聊。我们从平凡的解中得不到任何好玩的解。
当然，哈代认为 所有 自恋数都非常“平凡”。确实，这些数字不能算是最伟大的数学发现，但却是数学大道边上的美丽小道。不过哈代是对的，有趣的数学规律与纯粹巧合的事物应该有明确的区分。当然，只要你能牢记它们受到计数系统的限制，以这种方式来研究数的性质才有趣。研究特定计数系统下的性质，太容易钻入臭名昭著的数字主义了——相信你肯定不想被数字中虚假的性质禁锢吧。别忘了，数学研究的是“数”，而不是“数字”。
这就是数学家已经更加深入，不仅让数学研究脱离计数系统，甚至还要它脱离和任何客观存在之间的联系的其中一个原因。如果你真的想了解什么是“数”，这就是底线。我可以用一堆石块表示数，但也可以选择其他方法。5只鸭子可以代表5，5杯茶也可以，不过这些表示方式都涉及具体的物体。像这样把数学性质或概念从物理现实中分离出来的过程在数学中被称为抽象（abstraction）。但是要从“5个某种东西”中抽象出“5”这一概念并将其描述出来，实际上是很困难的事情。不过，还是有办法的。
数学家已经达成共识，所有包含5个事物的集合被命名为“5”。当我们说到“5”，实际上是在指所有五元组构成的抽象集合
。当我们写下5+3=8，意思是如果我们从“5”这个集合中取出某个五元组，再从“3”这个集合中取出某个三元组，将它们合并起来，会得到一个新的组合，它属于“8”这个集合。这个定义确实具有通用性，但啰唆得很。
数学的通用性意味着如果真有外星来客造访我们渺小的星球，数可能是我们之间唯一共有的东西。我们与其他碳基生物可能无法正常交流，甚至在同一光谱中看到的东西都不一样，但我们仍可以互相交换有关数的难题。如果你真的有幸身处外星人降临的现场，我可以给你两个选择。
第一个是哈代一定不喜欢的选择，也就是3,435这个数。这是一个明希豪森数（Münchhausen number），有点像自恋数，这也是明希豪森数以明希豪森男爵（Baron Münchhausen）的名字命名的原因。明希豪森男爵是18世纪的一位德国人，喜欢长篇大论，自吹自擂自己有多伟大。把明希豪森数的每一位数字做自身位数的乘方，然后求和，得到的结果还是这个数。3,435自然也是如此：3 3 +4 4 +3 3 +5 5 =3,435。这是十进制下除了平凡的1以外唯一满足这个条件的数，但其他进制也有这样的数，而且幸运的是，这些数对拥有12根手指的外星人也行得通。在十二进制下，3A67A54832就是一个明希豪森数。但真正的赢家是拥有13根手指的生物，它们有4个明希豪森数（33661、2AA834668A、4CA92A233518和4CA92A233538）。
第二个选择是37魔术，不过需要稍微改一改。虽然它确实和数字有关（而不仅仅与数本身有关），但可以修改成在任意进制下都成立的形式。在任何进制之下，对于一个数字，输入指定次数使其组成一个数，让它除以这几个数字之和，总会得到相同的答案。
所以并不是所有的数字游戏都只在一种进制下成立。好啦，我想这就是基数的全部内容了。