第6章
教我如何放得下

让我们从一个小小的挑战开始这一章的内容：找7枚2便士 的硬币，填充进第107页的正方形方框中。这是可能的，并且数学家还会肯定地告诉你，这个74.25mm×74.25mm 的方框是可以容纳7枚2便士硬币的最小方框。这个问题不仅仅适用于2便士的硬币，数学家可以肯定地告诉你，对于任意7个相同的圆，可以容纳它们的最小正方形的边长是圆直径的2.866倍。2便士硬币的直径是25.9mm，所以25.9mm×2.866 ≈ 74.23mm。拿着方框多晃一晃，这些硬币一定能放进方框里。

这太容易了？好，现在看你能否将31枚2便士硬币填充进边长为144.9546mm 的正方形。或许你还能打破这个记录。目前31枚2便士硬币的世界纪录是边长为144.9546mm的正方形，但没有数学家可以确定这就是最小的正方形。最高效的填充方式至今仍未被发现，最佳纪录或许正等着你来创造。事实上，最佳纪录已经确定下来的情况不多，只有硬币数不超过30的情况，以及硬币数为36这么一种额外情况。对于其他所有情况，都可能还有小小的改进空间。

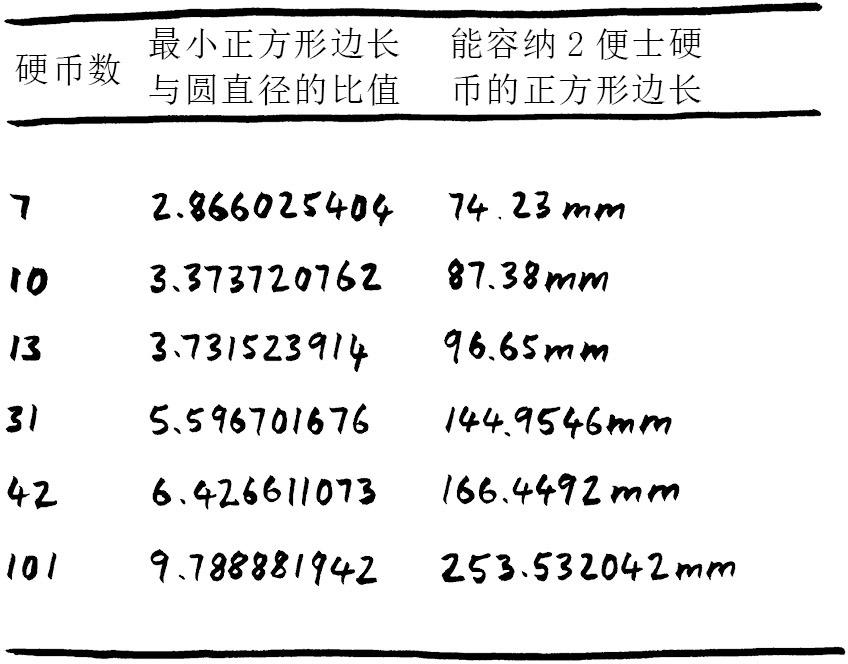
如果加大筹码，尝试将101枚硬币填进正方形。折腾几个小时之后，你可能开始思考，有没有更快的方法？真的有！计算机程序可以帮你（我可以向你保证这不是作弊）。对于从1枚硬币到10,000枚硬币的情况，计算机都已经找到了相当不错的解法。 但是，计算机会面临一个问题，也就是当你发现了摆放31枚硬币的更好方案时同样会面临的问题：你怎么知道这是不是已经到顶了呢？你怎么知道正方形的尺寸不能再小，里面的硬币数不能再多了呢？未来的日子惶惶不安，或许总会有某个人，在某一天，打破了你的纪录。

我对图形填充问题（packing problem）非常着迷。人类对如何将物体填充进另一个空间背后隐藏的数学知之甚少。这看起来是再简单不过的事情：只要将物体排列得足够紧凑，使它们占用最小的空间。但这事我们就是弄不好。不过，真正令人着迷的是，图形填充这一数学课题，仍是一片令人振奋的荒芜。历史上有很多数学领域也都经历过这种凌乱的阶段，直到一项革命性的突破让人们对该领域的认知达到全新的高度。你可能觉得很多数学领域都已经被数学家们探索完了，但这个领域还亟待重大突破。