




虽然这5种限量版柏拉图立体名扬至今,但实际上还有4种古人一无所知的柏拉图立体。(真的是,刚刚是平行线,现在又来这个。)我们可以让二维正多边形的边穿过另外一条边(即星形多边形),而不是形成角点,当然也可以让柏拉图立体的面相交而不是形成新边。欧几里得认为面不能相交,但我们可以做不同的假设。12个正五边形和20个正三角形分别形成新的柏拉图立体——大十二面体(the great dodecahedron)和大二十面体(the great icosahedron)。下面我们又进入奖金回合:用星形多边形制作星形多面体,这是星形的二次方。使用12个五角星形,每3个形成一个顶点,就可以形成大星形十二面体(the great stellated dodecahedron);每5个形成一个顶点,就可形成小星形十二面体(the small stellated dodecahedron)。
几个世纪以来,人们不断发现星形柏拉图立体。最早的实例来自威尼斯的教堂:艺术家保罗·乌切洛(Paolo Uccello)于1430年完成的一幅镶嵌图案中出现了小星形二十面体。1813年,法国数学家奥古斯丁·路易·柯西(Augustin Louis Cauchy)男爵继续推广欧几里得的工作,将理论发展完善,证明星形柏拉图立体只有大星形十二面体、小星形十二面体、大二十面体和大十二面体这4种。你可以用卡纸制作这4种图形
 ,不过面的相交要费些脑筋。
,不过面的相交要费些脑筋。

大十二面体、大二十面体、大星形十二面体和小星形十二面体
所有柏拉图立体,无论是不是星形的,都有一个共同的奇妙特征:每一个柏拉图立体里面都能怡好放入另一个柏拉图立体。这可以作为多面体派对上的一个小魔术:如果你在柏拉图立体的每个“面”(构成柏拉图立体的多边形)的正中心画一个点,那么肯定恰好能在里面放入一个柏拉图立体,它的顶点恰好和这些点重合。后者就被称为前者的对偶(dual)。十二面柏拉图立体的12个面的中心点恰好能和内部一个二十面柏拉图立体的12个顶点重合;二十面体的20个面的中心点恰好能和内部一个十二面体的20个顶点重合。同样的,立方体和正八面体互为对偶,四面体的对偶仍然是四面体。星形多面体也具有类似的特征,大星形十二面体和大二十面体互为对偶,小星形十二面体和大十二面体互为对偶。

保罗·乌切洛在威尼斯圣马可大教堂(Saint Mark’s Cathedral)设计的镶嵌图案
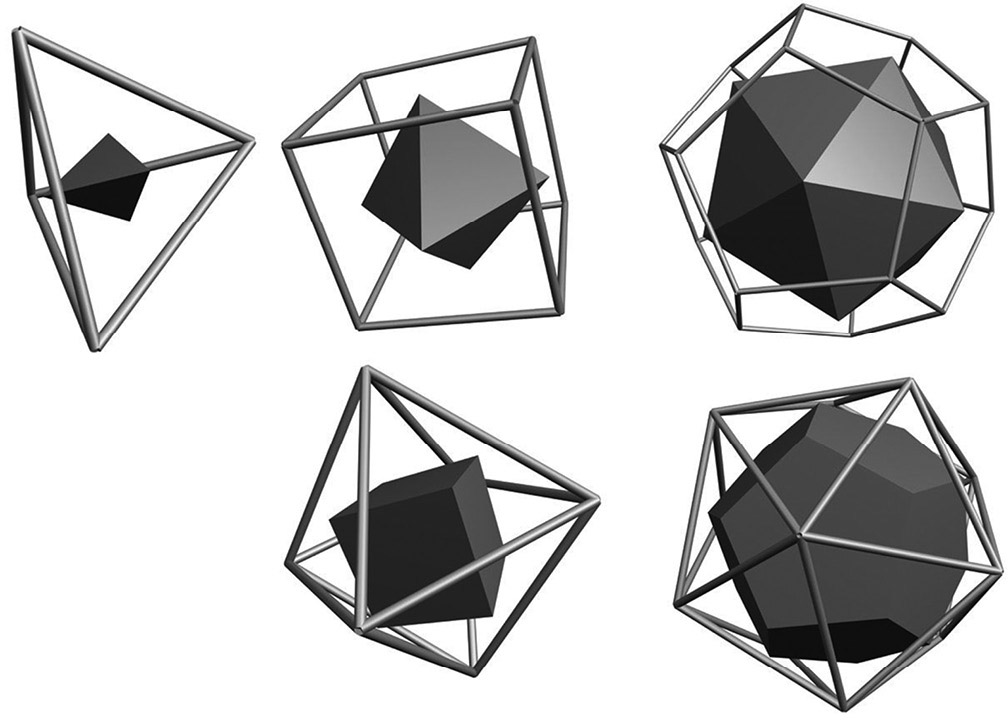
柏拉图立体及其对偶图形