下载掌阅APP，畅读海量书库
立即打开
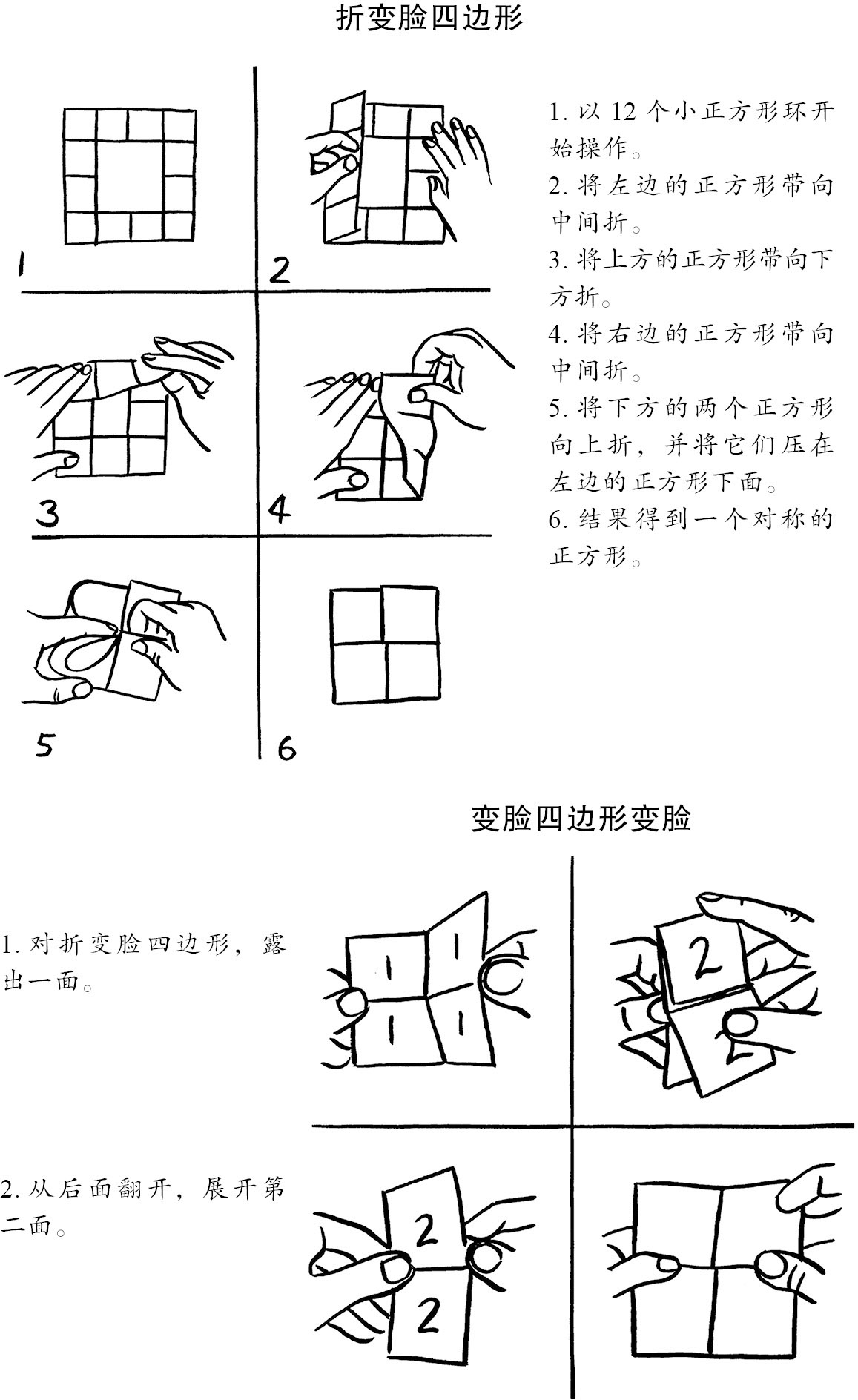
还有一种方法可以制作滚动图形，是种奇怪的方法。不过由此制作出来的这种奇怪形状不会在地上滚动，而是向自己内部滚动，不断变出新的面孔。比如，我们可以制作一个变换6个面的正方形。还等什么，快来动手吧！首先准备一张足够大的正方形纸，将它分成16个小正方形，将内部的4个小正方形裁掉，然后按照下面的教程一步一步地操作，最终折出的形状就是变脸四边形（tetraflexagon）。
为了跟踪面的变化，我们可以在4个小正方形的正面写上数字1，在背面写下数字2。（一旦你掌握了变脸多边形的窍门，你会发现更多有创意的标记方式……）将这个方块对折，你会发现有两种方式可以重新打开它。一种会回到开始的状态，而另一种会让你得到新的面。将4个新的正方形标记上数字3，然后合上再打开……不同的面会出现、消失，就像我们小时候玩的“折纸预言”游戏
的高科技版本。将一个图形合上再打开到不同面的过程被称为变脸，这就是为什么这些图形被称为变脸多边形。本例中的图形被称为变脸四边形，因为这个图形有4条边。不断变脸，直到你找到所有面，并做好标记（标记是为了防止你原路返回），一共应该有6个面。
上面这个例子只是众多变脸多边形中的一种。下面要介绍的这种多边形基于六边形，所以被称为变脸六边形（hexa-flexagon）。它由一条长长的等边三形链折叠而成。在书后的“疑难解答”中，我分别给出了包含3个面和6个面的变脸六边形教程。这两种变脸多边形分别叫作三面变脸六边形（trihexaflexagon）和六面变脸六边形（hexahexaflexagon）。先前的变脸四边形全称应为六面变脸四边形（hexatetraflexagon）。（命名方式通常是X面变脸𝑌边形。）
变脸六边形的变脸方法是捏住一条从中心出发的折痕同时将其相对的折痕向中间推。将它合起来后，你会发现有一面可以从中心打开。打开并整理平整，你就会得到一个新的面。
变脸多边形是由著名的数学专栏作家马丁·加德纳（Martin Gardner）首次带入公众视野的。1959年，他在《科学美国人》（ Scientific American ）的专栏上写了第一篇有关变脸多边形的文章。他的专栏向世人介绍了他沉迷的趣味数学。我第一次知道他是通过他在1959年出版的书《科学美国人之趣味数学难题与游戏大全》（ The Scientific American Book of Mathematical Puzzles and Diversions ）。截至1961年，除了变脸六边形，加德纳还向世人介绍了三面变脸四边形和四面变脸四边形。探索变脸多边形的行动至今仍在继续，变脸五边形、变脸八边形、变脸十二边形相继被发现。它们变脸的方法都很怪异。在最近的一次数学会议上，还有一个人激动地向我展示了十面变脸十边形，仅这一点，就让我觉得不虚此行。
变脸多边形的历史还很短。最早发现的是三面变脸六边形，那时已经是1939年了。当时英国数学家亚瑟·斯通（Arthur Stone，保罗·埃尔德什的同事）在美国工作，为了让美式纸张夹进英式活页夹，他将纸张裁去一些纸条。随后他漫不经心地将一些纸条折叠成等边三角形——嘿！他居然无意间折出了三面变脸六边形。不久，他的几个朋友（包括诺贝尔物理学奖得主理查德·费曼）也加入了他的队伍，组成普林斯顿变脸多边形委员会（Princeton Flexagon Committee）。他们最初的一个发现是塔克曼遍历［Tuckerman traverse，命名自委员会成员布莱恩特·塔克曼（Bryant Tuckerman）］。这个发现指出，在变脸六边形的一个顶点不断变脸直到没有新的面出现，然后换到相邻的顶点，继续变脸直到没有新面出现，这样一定可以得到所有可能的面。（如果你随机变脸，有些面可能不会出现。）
下面给你的挑战有点复杂。对于六面变脸四边形，要找到所有6个面很容易。初始状态，你可以看到前后两个面（出于方便，通常我会标记为F和B），每个面均可水平或竖直翻折变出新面，这4种操作会显示其余4个隐藏面（可以依次标记为F V 、F H 、B V 、B H ）。我要给你的挑战是，找出可以同时外露的相对两面。例如F面和B面显然可以同时外露。试试看，你可以让F V 和B H 在两侧同时出现吗？有些组合可以出现在相对的位置，而有些则不行。（详情请参阅书后的“疑难解答”。）
接下来，你可以大开脑洞进行创意标记啦。你可以在各个面上写下同事的名字及办公室琐事。这些组合看似复杂且随机，但你其实可以控制它们。“不好意思，梅维斯，我不知道为什么又是你来沏茶，但变脸多边形显示的确如此。”你还可以为圣诞派对准备一个特制的变脸多边形，决定谁可以不买单。
我曾制作过一个六面变脸六边形的啤酒杯杯垫，在每一面写下不同的酒，并记录该轮到谁喝。如果你想制作精美巧妙的名片，还可以将六面四边形推广成直角形，即长方形，这样就能获得普通名片的3倍面积而不必改变名片的大小。我就有用这种名片的需求，幸好我有另一张名片来解释第一张该怎么看。
