




在我打出这些字的时候,我面前的桌面上放着一枚百慕大(Bermuda)的三角形硬币——百慕大铸币厂于1998年制造的限量版3美元硬币。限量是非常正确的选择:这种三角形硬币一点也不实用。历史上的硬币通常都是圆形的,因为圆形更容易铸造,并且没有尖锐易损棱角的硬币更适合随身携带(尖锐的棱角会不断与口袋或钱包的衬里摩擦,甚至戳出一个大洞)。在现代社会,将不同面额的硬币设置成不同的直径可以让机器很容易区分它们,比如自动售卖机:圆形硬币可以顺着售卖机内部的轨道滚下,不管硬币朝向如何,售卖机都可以根据直径识别它们。如果采用方形的硬币,则问题多多,因为在滚动过程中,它的宽度(与圆的直径类似)会不断改变。
我很想知道换成三角形硬币会发生什么,于是我从网上搜获了一枚(购买价格已远超原本的面值三倍),这样我便可以仔细研究一番。真品认证书上列出了一系列官方数据:它由20克925纯银制成(这让我觉得我没有被骗),总发行量为6,500枚,直径为35mm。且慢!为什么三角形会有直径?三角形的跨距应该会随着测量位置不同而改变,但真的是这样吗?于是我拿了一把尺子,在几个不同方向上测量这枚硬币,跨距确实都是35mm,认证书的标注(以及精度)没有错。这是因为这枚3美元面值的百慕大硬币不是普通的三角形。
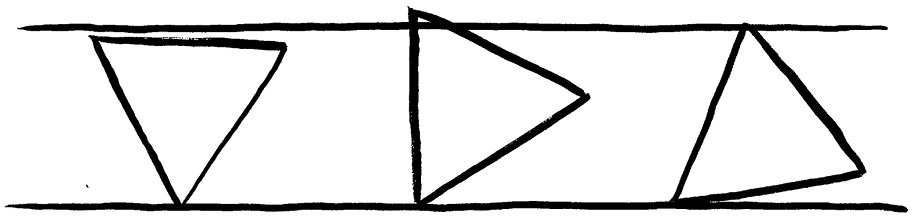
轻微地旋转一个三角形,它会短暂地变高

曲边三角形和百慕大硬币
实际上,这个图形我们已经见过了。回翻“构造平面图形”那一章的插图(第32页),为了画出等边三角形,我们绘制了3个相交的圆。这个硬币的形状就隐藏在几条时常被我们忽视的作图线中。若用直线连接3个交点,就能连成一个三角形,若用3条圆弧连接,就能连成曲边图形,3美元硬币正是这种形状。另外,这个图形也隐藏在比萨问题的解法中。
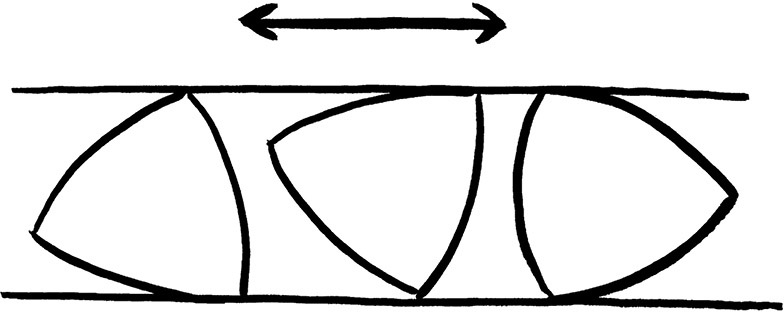
这个三边图形除了可以完美平分比萨,还有一个非常重要的性质:不管怎么放置,它的高度总是相同的。这意味着它可以滚动起来。如果将翻滚者的两个圆片并排平放在桌面上,夹在两把平行的直尺间,它们很容易滚动起来,因为圆的宽度不会改变(出于某些原因,我们用“宽度”来描述这种性质,而不用“高度”和“直径”)。接下来,我们再找一些卡纸,将圆规两脚的距离扩大到10cm,像第二章那样画出3个包围等边三角形的相交圆(不必画出整个圆,只需画出形成三边形的3条边即可),并将这个图形剪下,然后如法炮制,再剪出第二个。如果将它们夹在两把平行的直尺间,它们依然可以轻松地滚动。你也可以将其中的一个替换成圆,不管怎样,直尺间的距离总是保持在10cm。
如果你嫌上面的操作太麻烦,可以找一些20便士或50便士的硬币。它们都是正七边形,不过是曲边七边形。你也可以用卡纸做出这个图形:将圆规的针脚固定在正多边形的每一个顶点,画出经过对边两端点的圆弧。利用这个方法可以画出任意奇数边的正曲边多边形。不管是50便士硬币,还是你用圆规和卡纸画出的图形,都可以在两把平行的尺子间完美地滚动,所以奇数边的七边形50便士和20便士硬币依然可以在自动售卖机中使用,尽管它们不是圆形。不过,澳大利亚从1969年开始就一直使用十二直边硬币,英国也在2017年引入一种直边硬币,售卖机可以接受合理范围内的宽度变化,所以将硬币做成曲边或许是多余的。
曲边等边三角形有很多奇妙的性质,这使得它获得一个专属名字:勒洛三角形[Reuleaux triangle,命名自19世纪德国工程师弗伦茨·勒洛(Franz Reuleaux)]。它除了可以用于铸造硬币,还可以用在钻头中,这种形状的钻头可以打出近似正方形的洞。但在现实中,它的用处并没有这么大,因为很少有方形截面的钉子,而圆形截面钉子和方形孔又不相容。然而,美国专利局在1978年确实接收了一项勒洛三角形钻头的专利(专利号为4074778),它用于开采煤矿。我猜这项专利直到现在仍然无人竞争,鲜有人用。