





在本章开始之前,我们要做一些好玩的事。快把剪刀准备好,但当心别让剪刀伤着自己。在这一章中,除了剪刀外,我们还要用到一副圆规(好吧,其实是一个圆规)。找一些足够厚但又稍微有点褶皱的卡纸,比如纸箱的纸板,从上面裁出两个直径为10cm(即半径为5cm)的圆。你既可以使用圆规来确定尺寸,也可以将本书的模板裁下,放在卡纸上,绕着它的圆周剪出两个圆。裁剪完毕后,再确定它们的圆心(如果你是用圆规画圆,就不需要这一步了,因为圆规尖脚扎出的孔洞就是圆心),然后从边缘往圆心方向裁出一条细开口,长度为半径的29%(半径为5cm的圆,要裁的长度大约为1.5cm)。开口要足够宽,确保两个圆能够相互嵌入。将这两个相互嵌入的圆片放在桌子上,让它们滚动起来,我们便可欣赏到这个奇异装置的怪异运动方式了。
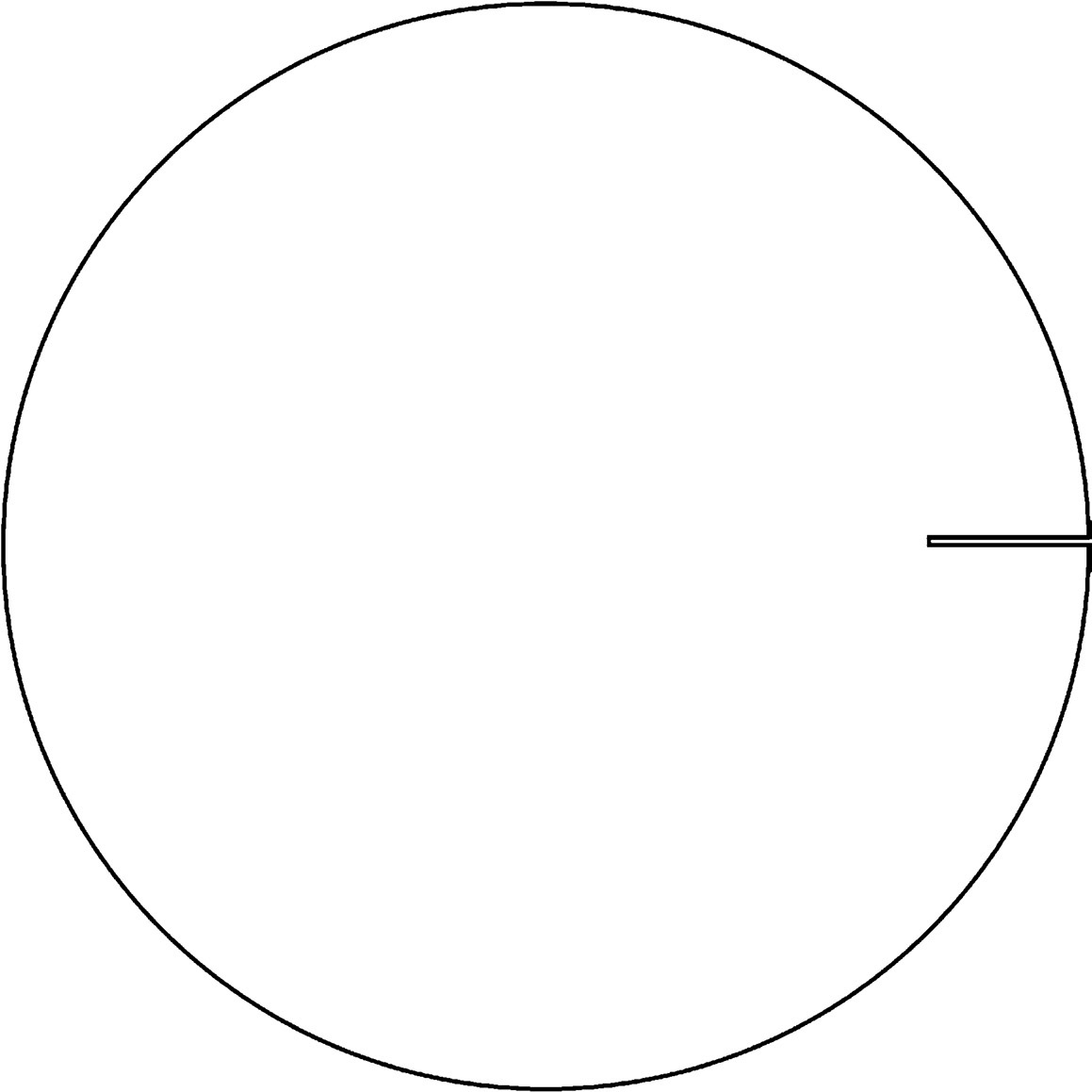
按照这个模板裁出组成翻滚者的两个圆片
这个装置名为翻滚者(Wobbler)。只有当两个圆相交的部分恰到好处,它才会一直翻滚。如果两个圆相交过多,翻滚者翻滚几下就会停在位置A,见第65页图所示,两个圆片与桌面的夹角都是45度;如果相交太少,那么翻滚者就会停在位置B,有一个圆片直立着,与桌面成直角。只有开口的长度恰好是半径的29.2893%,翻滚者才能一直翻滚下去。当然,由于摩擦力和空气阻力的作用,它还是会慢慢减速停下来(而且我们也不可能精确地切出小数长度的开口),但是让翻滚者滚过整张桌面甚至整间屋子还是有可能的。

翻滚者之所以能够不停地滚动,是因为它的重心(centre of gravity,物体质量的中心)高度在翻滚过程中一直保持不变。它的稳定水平足以让它在世界水平的比赛中保持冠军水准。由于提升重心需要做功和消耗能量,物体不会自己往高处跑。因此,如果物体在平面上滚动需要不断提升重心高度,那么它就不会自动滚起来。这就是为什么圆可以做成轮子:在滚动过程中,圆的重心会一直保持在同一高度。这也是为什么正方形轮子会很糟糕:即使用力撞击它,它也不会滚动。要让正方形滚起来,需要大力抬起它使其单角着地,然后让它再从另外一个方向落下去。圆可以在平面上自动滚动下去,但是要使方块不断滚下去,你就得不断地施加作用力。
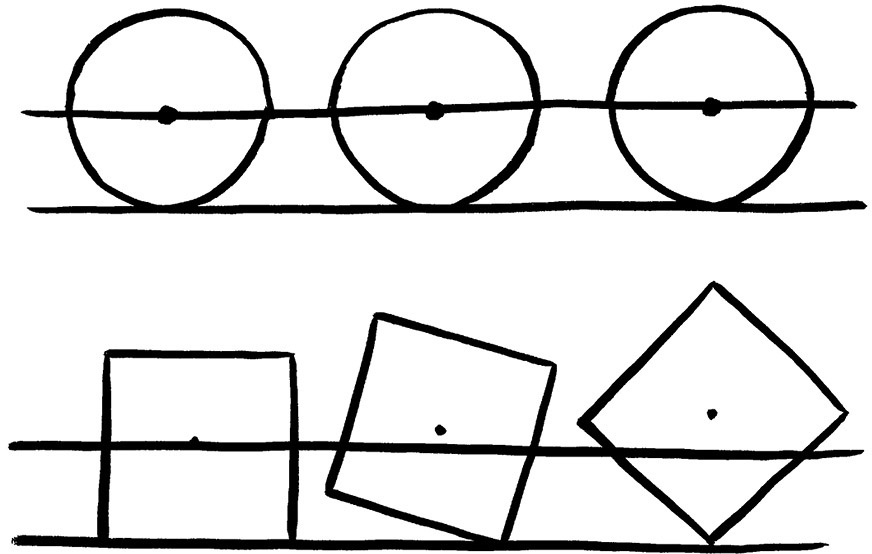
仔细看,上面的圆其实正在滚动中
你可以证明,当翻滚者处于位置A和位置B时,其重心高度是一样的。这其中运用到的最复杂数学原理也只是毕达哥拉斯定理。你可以在书后的“疑难解答”找到完整的证明,包括开口的长度为什么要取半径的29.2893%(简单来说,这样可以使两个圆盘的中心距离恰好是
 ×半径长度)。神秘的
×半径长度)。神秘的
 再一次出现,把我们带回到平方根。不过,要证明重心高度不变却要费一番周折,数学家戴维·辛马斯特(David Singmaster)于1990年成功地给出了这个证明。这个翻滚者的重心虽然高度不变,却会前后摇摆,这就是为什么翻滚者会在前进过程中东倒西歪,就像喝多了一样。
再一次出现,把我们带回到平方根。不过,要证明重心高度不变却要费一番周折,数学家戴维·辛马斯特(David Singmaster)于1990年成功地给出了这个证明。这个翻滚者的重心虽然高度不变,却会前后摇摆,这就是为什么翻滚者会在前进过程中东倒西歪,就像喝多了一样。
我能找到最早提及翻滚者的文献出自1966年《美国物理期刊》( American Journal of Physics ),作者为A. T.斯图尔特(A. T. Stewart)。当时他将其命名为二圆滚动者(Two-circle Roller)。人们使用圆形的轮子已经有上千年的历史。轮子可以看作是人类的第二项伟大发明(排名仅次于火,比切片面包稍微靠前)。因此,我很惊讶直到20世纪60年代,人们才发现这种使圆滚动的新方法。这种方法对椭圆(ellipse)也奏效。正如正方形是四边等长的长方形,圆则是长半径与短半径相等的椭圆。虽然椭圆不能像传统轮子那样滚动,但你仍然可以利用两个椭圆圆片制成一个翻滚者。不过要注意的是,不同椭圆的开口长度是不同的。

两个椭圆的中心距离等于
 ×
×
 ,而不再是
,而不再是
 ×半径
×半径
然而,在完美有效的滚轮中,我们不能过早排除正方形。在特定的曲面上,正方形也可以非常轻松地滚动起来,比如我们可以让路面颠簸一点来抵消正方形滚动时重心的上下移动。要让正方形优雅地跳舞,只有一种曲线能够满足我们的要求,那就是悬链线(catenary)。之所以起这个名字,是因为它是由一条锁链两端悬挂形成的图形;另外,锁链(chain)在拉丁文中是“ catena ”。举起一段锁链的两端,你就能看到这种曲线了(注意,绳子太轻,靠自身重力可能无法形成悬链线)。将悬链线翻转,反复拼接在一起,正方形就可以轻松地在这种路面上滚动啦。不仅正方形如此,几乎所有的图形,我们都可以找到一种奇怪的颠簸路面,使其在上面轻松滚动。

这个就是骑得很舒服的表情