美国国家航空航天局与数

让我们再次回到本章开头的话题。这就是为什么我认为美国国家航空航天局把 计算到那么多位完全是出于有趣。乐趣是大部分数学家和数学爱好者的动力。我还发现了另外一条重要线索。网站上说，这些数字是罗伯特·涅米洛夫（Robert Nemiroff）在美国国家航空航天局“利用业余时间，使用VAX-alpha型计算机历时数周完成”的。这似乎说明美国国家航空航天局工程师身边刚好有一台空闲的超级计算机，他们觉得可以仅仅出于好玩就让它在周末运行一个程序。此外，他们还计算了其他一些数的平方根。

我没法责备他们，而且计算平方根对于计算机的性能而言也是一项重大的检验，因为这是一项永远也不会完成的任务。对于平方数，找到它们的平方根很容易，这些数都是一些好看的整数。利用平方根符号 ，我们可以记 =1、 =2、 =3等，但是对于非平方数的平方根，比如 ，它们的小数无穷无尽。这就是为什么美国国家航空航天局可以计算出超过100亿位小数——它的小数位永远不会终结。即使你对 前100位求平方，结果也不会恰好等2。

有一天，我很无聊，于是想看看能不能找到一种数——其平方根的数字里有和该数一样的数字序列。我还真找到了一些！最后我找到了所有这样的数。我将它们命名为嫁接数（grafting number），因为这些数的“根”像是从它自己身上长出来的一样。但是仅仅发现它们对我来说远远不够，作为一个数学迷，我想到达更高的层次。

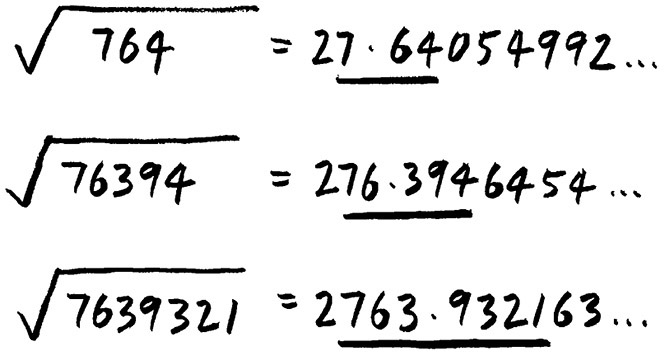
发现并记录这样的数就像集邮，我要做的事情就是写下这些数并给它们命名。这完全是一种数学乐趣，因为真正的数学总会驱使你去发现它们背后的普遍规律。这是从叙述事实到解释原理的一步阶梯。通过不断尝试，我发现了这些嫁接数的来源：它们都来源于3- 的结果。每次从上述算式结果中截取奇数个数字，向上取整，便会得到所有嫁接数。我自豪地将3- 命名为嫁接常量（grafting constant）。

有一些数学家对我的嫁接数进行了更深入的研究。在我看来，当他们不再单纯考虑数学的实际应用时，便能抓住使数学成为一门艺术的关键要素。第一要素是发现并描述规律；第二要素是探明这些规律的原因并证明这些规律的普适性；最后一个要素是，所有这一切仅仅出于乐趣，纯粹为了好玩。 LmQpcoP8dJyu+HSB8SukDIQvGIDyaYxOHeDo1Shzd0MoyESRyx+a9sfDIw7uNkb8