下载掌阅APP，畅读海量书库
立即打开
有些问题是古希腊人不能用尺规解决的，比如将一个角三等分，或者画出面积相等的圆和正方形，这些问题快把他们逼疯了。但问题是，他们又无法证明这些问题是不可能解决的（当然，我们现在已经知道这些问题确实是不能通过尺规完成的），所以对他们来说，只要足够聪明，一定能找到解决方法。毕竟对于三等分角这种简单的问题，人们理所当然地认为它不可能无解。
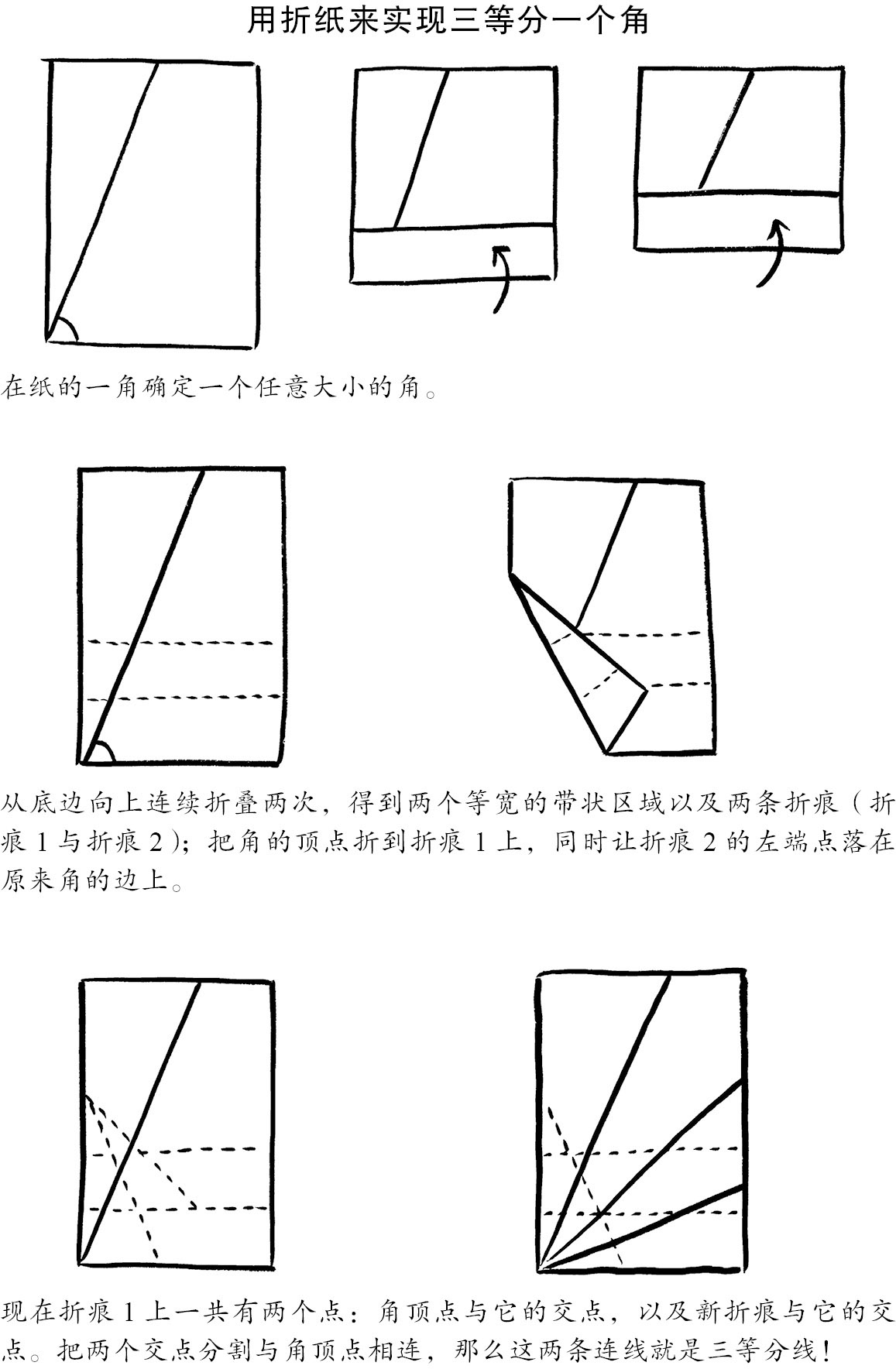
不过，外星人可以轻松地通过折纸的方式解决这个问题，上图就是用折纸三等分角的一种方法。它由日本北海道大学（Hokkaido University）的阿部恒于1980年首次提出。古希腊人之所以没有发现这种方法，是因为它需要用两条不同的直线同时连接两个不同的点。这种操作超出了尺规作图的使用范围，却能通过折纸轻松做到。
有些图形的某些边和另一些边相交，这更令古希腊人发疯。如果你把之前折出的五边形纸结靠近灯光看，会发现里面有个五角星，这种形状通常被称作五角星形（pentagram）。正五边形和正五角星形都是5条边相等的五边形，但五角星的这个特征经常被忽视，因为它各边是相交的。有人认为五角星形不是“真”的图形，真令人羞愧。但我认为这属于个人喜好的问题，我就喜欢边相交的图形。
如果你不喜欢边相交的图形，那么你只能找到一种正七边形（heptagon），但如果你不介意一点随性的“交流”（就让我们面对现实吧，这个时代谁不是这样呢），那么你就会找到两种完美的正七边形。如果把全部图形包括在内，一共有5种不同的正十一边形（hendecagon）。在只有一种正规形状（regular form）的图形中，正六边形是边最多的图形；其他边数大于6的正多边形一般有两种或两种以上。然而，并不是边越多，正规形状就越多。例如，正十二边形（dodecagon）就只有2种。
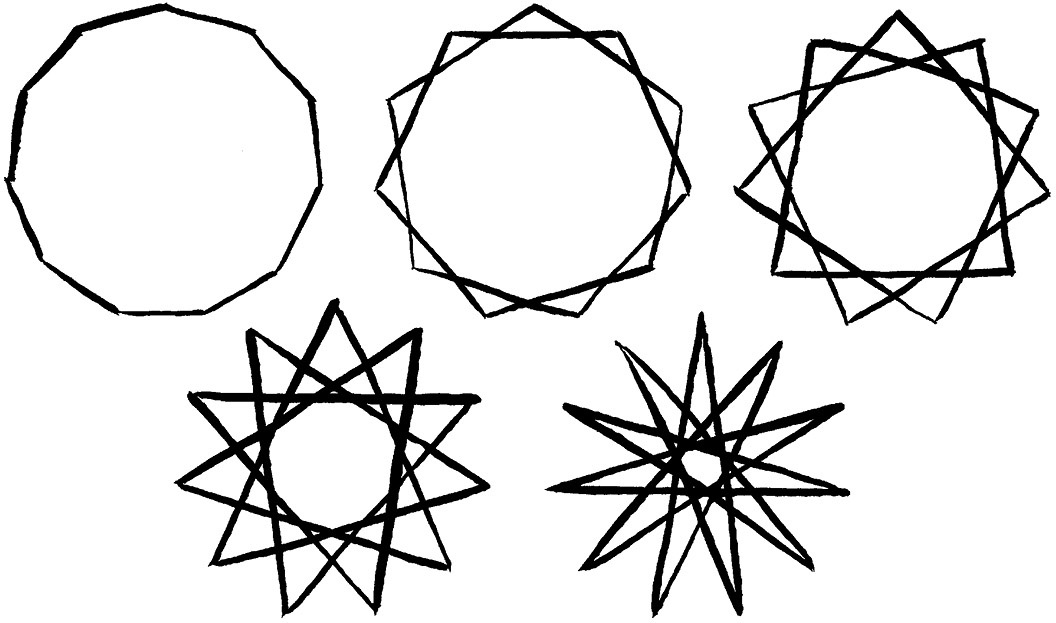
5种不同的正十一边形
让我感到遗憾的是，每当画星形时，人们总是只想到五角星形。为何不画七角星形甚至九角星形呢？值得一提的是：如果你打算练习画不同的星形，最难的一步是让角点分布得足够均匀。下面是一些为你准备好的模板，你可以在上面画星形。你还可以在makeanddo4D.com这个网站上下载到更多免费模板。
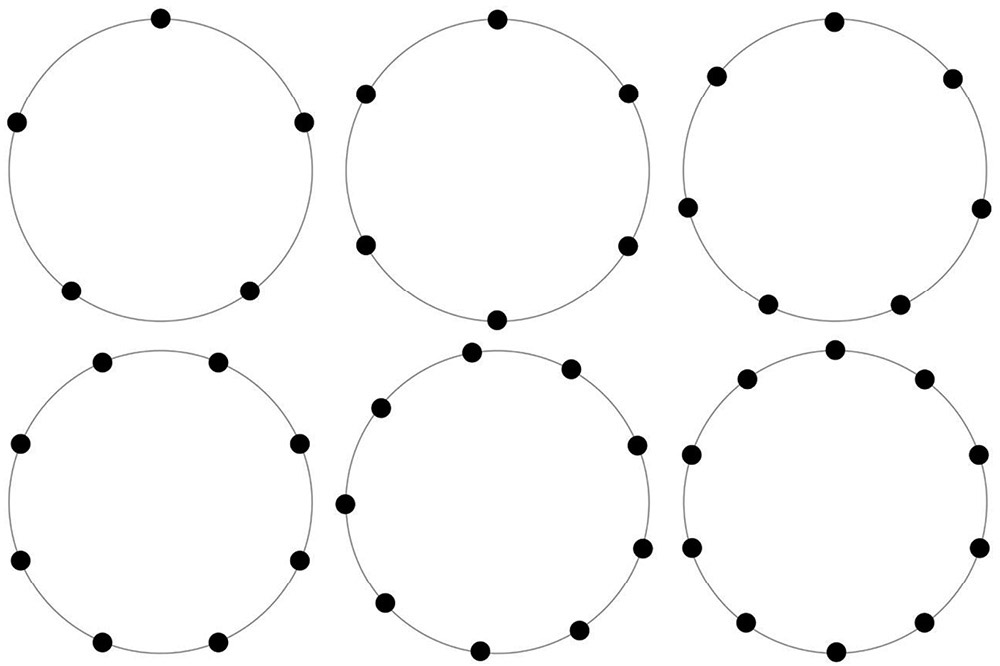
让古希腊人为难的最后一个问题是：怎样在他们刻板的规则下画出正七边形。这个问题令他们彻底发疯。经过大量尝试，他们画出了正五边形，但无法攻克正七边形。于是他们决定把它搁置一边，先去尝试画其他图形。他们用尺规画出正八边形和正十边形，但无法画出正九边形和正十一边形。往后，十二边形很容易画出，但十三边形和十四边形又画不出来了。
令人沮丧的是，古希腊人还不够了解数学，以至于他们无法证明尺规画不出这些图形，所以他们一直在做无用的努力。
我要强调一点，古希腊人不是没有能力画出这些图形，他们只是无法用自己执着的方法画出这些图形。只要一点尝试和接受一点误差，你只需一把直尺就能画出相当精确的正七边形，足够满足实际需求了。但对欧几里得和他的朋友们来说，这不是真正完美的正七边形，这令他们非常懊恼。他们只接受直线和完美圆的存在，如果无法用直线和圆画出正七边形，他们会不满意。如果正七边形没有从根本上得到证明（从直线和圆开始证明正七边形可以画出），他们不会承认正七边形的存在。
不过在我看来，古希腊人太死板了。他们完全可以只借助于直线和圆来三等分角，只需要在一个地方画一个圆，然后将它滑动到另一个地方。但古希腊人认为这种操作不符合规定，因为它们无法用尺规实现。那是他们的特权，数学是一场规模宏大的游戏，古希腊人只是在自己建立的规则下小心行事。数学同样是一场严格的游戏，你无法作弊
，你只能在其中添加更多规则。
这可能是我最喜欢的对数学的定义：数学是一场你可以自己制定规则的游戏，你自己制定游戏规则——你可以确定哪些事情是正确的，哪些事情是允许的，然后从规则开始，一步一步深入，证明更多的事实。数是最简单的：你只需假设它们存在，就可以开始证明“十进制的自恋数不超过39个”这样的命题。数的世界非常有价值，因为你只需要一个假设：假设数的确存在。另一方面，几何却有更多选择起始假设的余地。数学的伟大在于，一旦确定了基本假设，任何人在宇宙乃至宇宙外的任何地方都会得到同样的结果。如果我们知道某个外星文明的几何基本假设，那么我们就能推导出和他们完全一样的结果。