





没有什么比现实主义更不真实了……细节令人困惑。只有通过选择、通过消除、通过强调,我们才能获得事物的真正意义。
乔治娅·奥·吉弗(Georgia O' Keeffe)
本章将通过科学的方法来引入多模型思维。我们先从孔多塞陪审团定理(Condorcet jury theorem)和多样性预测定理(diversity prediction theorem)入手讨论,这两个定理为证明多模型思维在帮助人们行动、预测和解释方面的价值提供了可量化的论据。需要指出的是,这两个定理可能夸大了许多模型的情况。为了说明原因,我们又引入了分类模型(categorization model),它将世界划分为一个个箱子。使用分类模型的目的是表明构建多模型可能会比预想的更难。然后,我们利用这类模型讨论了模型粒度(model granularity),也就是模型应该有多具体,并帮助我们决定是采用一个大模型还是多个小模型。选择取决于用途:在预测时,我们经常需要大模型;而在解释时,小模型则更好一些。
我们得到的结论解决了一个长期以来挥之不去的忧虑:多模型思维可能需要学习非常多的模型。是的,虽然我们必须学习掌握一些模型,但是并不需要学习像有些人想象的那么多。我们不需要掌握100个模型,甚至连50个也不需要,因为模型具有一对多的性质。我们可以通过重新分配名称、标识符,或者修改假设来将任何一个模型应用于多种情况。模型的这个性质很好地平衡了多模型思维的需求。事实上,在新的领域应用模型对创造力、开放性和怀疑精神的要求也非常高。我们必须认识到,并非每个模型都适合每项任务。如果一个模型无法解释、预测或帮助我们推理,那就必须将它放到一边,考虑其他模型。
这种一对多的技能,与许多人所认为的要成为一名优秀建模者所必需的数学和分析才能是不同的。一对多的过程对创造力的要求很高,它实际上相当于在问这样一个问题:对于随机游走,我能够想到多少种用途?作为这种创造力的一个例子,在本章的最后,我们将几何学中的面积公式和体积公式作为模型,解释了超级油轮的大小、评估了身体质量指数、预测了新陈代谢的比例……并解释为什么我们很少看到女性CEO。
现在来看看正式模型,它们有助于理解多模型思维的好处。在这些模型的情境下,我们描述了两个定理:孔多塞陪审团定理和多样性预测定理。
孔多塞陪审团定理是从一个解释多数规则长处的模型中推导出来的。在这个模型中,陪审员要做出要么有罪、要么无罪的二元决策。每个陪审员正确决策的时候比错误的时候多。为了将这个定理应用于模型集合而不是一组陪审员,我们将每个陪审员的决策解释为模型的一个类别。这种分类可以是行动(买入或卖出),也可以是预测(美国民主党胜出还是共和党胜出)。孔多塞陪审团定理告诉我们,通过构建多个模型并使用多数规则,将比只使用其中一个模型更加准确。这个模型依赖于世界状态(state of the world)的概念,它是对所有相关信息的完整描述。对于一个陪审团来说,世界状态包括了审判时呈现的所有证据。对于那些衡量某个慈善项目的社会捐献的模型来说,世界状态则可能与项目的团队、组织结构、运营计划以及项目所要解决的问题的特征或状况相对应。
孔多塞陪审团定理
总数为奇数的一组人(模型)将未知的世界状态分为真或假。每个人(模型)正确分类的概率为 p >1/2,并且任何一个人(模型)分类正确的概率在统计上都独立于任何其他人(模型)分类的正确性。
孔多塞陪审团定理: 多数投票正确的概率比任何人(模型)都更高;当人数(模型数)变得足够大时,多数投票的准确率将接近100%。
那么,如何将这个定理的原理应用于多模型方法呢?生态学家理查德·莱文斯(Richard Levins)对此给出了详细的阐述:“因此,我们尝试用几个不同的模型来处理同一个问题,这些模型的简化方法各不相同,但都有一个共同的生物学假设。如果这些模型(尽管它们有不同的假设)都导致相似的结果,那我们就得到了一个强有力的定理,它基本上不受模型细节的影响。因此,我们的真理就是若干独立的谎言的交集。”
 需要注意的是,在这里,莱文斯渴望达成一致的分类。当许多模型都给出了相同的分类时,我们会信心大增。
需要注意的是,在这里,莱文斯渴望达成一致的分类。当许多模型都给出了相同的分类时,我们会信心大增。
多样性预测定理则适用于给出数值预测或估值的模型,它量化了模型的准确性和多样性对所有模型平均准确性的贡献。

多样性预测定理
多模型误差=平均模型误差-模型预测的多样性,即:
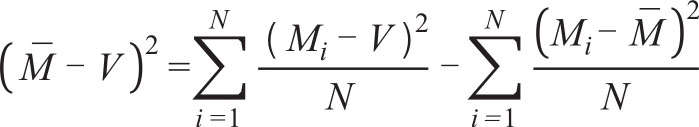
在这里,
M
i
表示模型
i
的预测,
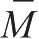 等于模型的平均值,
V
等于真值。
等于模型的平均值,
V
等于真值。
多样性预测定理描述了一个数学恒等式。我们用不着费心检验,因为它总是成立。下面举一个例子来说明这一点。假设我们用两个模型来预测某一部电影会获得多少项奥斯卡奖。一个模型预测它将获得两项奥斯卡奖,另一个模型则预测它将获得8项。这两个模型预测的平均值,也就是多模型预测的结果等于5。如果最后这部电影获得了4项奥斯卡奖,那么第一个模型的误差等于4(2 2 ),第二个模型的误差等于16(4 2 ),而多模型误差则等于1,模型预测的多样性等于9(因为每个模型的预测与平均预测均相差3)。这样一来,多样性预测定理就可以表达为:1(多模型误差)=10(平均模型误差)-9(模型预测的多样性)。
这个定理的原理在于,相反类型的误差(正负)会相互抵消。如果一个模型的预测值太高,同时另一个模型的预测值太低,那么这些模型就会表现出预测多样性。两个模型的误差相互抵消,模型的平均值将比任何一个模型更加准确。即便两个模型的预测值都太高,这些预测值的平均误差仍然不会比两个高预测值的平均误差更糟。
但是,多样性预测定理并不意味着任何不同模型的集合的预测必定是准确的。如果所有模型都有一个共同的偏差,那么它们的平均值也会包含那个偏差。不过,这个定理确实意味着,任何多样性的模型(或人)的集合将比其普通成员的预测更加准确,这种现象就是通常所说的“群体的智慧”(wisdom of crowds)。这是一个数学事实,它解释了计算机科学中集成方法(ensemble method)成功的原因,这种方法对多个分类加以平均,也解释了使用多个模型和框架进行思考的人比使用单个模型的人预测的准确性更高的事实。任何一种看待世界的单一方式都会遗漏掉某些细节,使我们更容易产生盲点。单模型思考者不太可能准确预测到重大事件,例如2008年的金融危机。

这两个定理为我们利用多个模型提供了令人信服的理由,至少在进行预测的情况下。然而,这个理由在一定意义上可能显得过强。孔多塞陪审团定理意味着,如果有足够多的模型,我们几乎永远不会犯错。多样性预测定理则意味着,如果能够构建一组多样的中等准确性的预测模型,我们就可以将多模型误差减少为接近于零。但是,正如接下来将会看到的,我们构建多个多样性模型的能力是有限的。
为了说明为什么这两个定理可能会“夸大其词”,现在来讨论一下分类模型。这类模型为孔多塞陪审团定理提供了微观基础。分类模型将世界状态划分为不相交的。最早的分类模型可以追溯到古希腊时代。在《范畴篇》( The Categories )一书中,亚里士多德描述了对世界进行分类的10个范畴,包括了实体(substance)、数量(quantity)、地点(location)和状态(positioning)等,每个范畴都会创建不同的类别。
当我们使用一个普通名词时,“裤子”是一个类别,“狗”、“勺子”、“壁炉”和“暑假”也是如此。我们就是在使用类别去指导行动。我们按种族,比如意大利人、法国人、土耳其人或韩国人,来对餐馆进行分类,以便决定在哪里吃午餐;按照市盈率对股票进行分类,并根据市盈率高低买卖股票。当人们声称亚利桑那州的人口之所以增长是因为该州气候宜人时是在用分类方法进行解释。我们还使用类别进行预测,例如预计身为退伍军人的候选人在选举中会有更大的获胜机会。
我们还可以在智慧层次结构中解释分类模型的作用。对象构成了数据,将对象分为不同类别就能创造出信息,而将估值分配给各个类别则需要知识。为了评价孔多塞陪审团定理,我们依赖一个二元分类模型,它将对象或状态分为两个类别,一类标记为“有罪”,另一类标记为“无罪”。关键的思想是,相关属性的数量限制了不同类别的数量,因此也就限制了有用模型的数量。
分类模型
存在一组世界的对象或状态,每个对象或状态都由一组属性定义,每个属性都有一个值。根据对象的属性,分类模型M将对象或状态划分为一个有限的类别集{ S 1 , S 2 ,……, S n },然后给每个类别赋值{ M 1 , M 2 ,……, M n }。
假设有100份学生贷款,其中有一半是按期还款的,另一半是违约的。我们知道每一笔贷款的两个信息:第一,贷款金额是否超过了5万美元;第二,贷款者主修的工科还是文科。这是两个属性。通过这两个属性,我们可以区分出4种类型的贷款:主修工科学生的大额贷款、主修工科学生的小额贷款、主修文科学生的大额贷款以及主修文科学生的小额贷款。
二元分类模型将上面这4种类型中的每一种都分为按期还款与违约。一种模型可能将小额贷款归为按期还款,将大额贷款则归为违约。另一种模型则可能将主修工科学生的贷款归为按期还款,将主修文科学生的贷款归为违约。我们有理由认为这两种模型中的任何一个都可能在超过一半的情况下是正确的,而且这两种模型大体上相互独立。
但是,当我们尝试构建更多的模型时就会出现问题。要将4个类别映射为两个结果,最多只有16个模型。上面这两个模型是其中的两个,它们将所有贷款分为按期还款或违约。剩下的14个模型中的每一个都有一个完全相反的模型,只要某个模型的分类是正确的,那么与之相反的那个模型的分类就是错误的。因此,在14个可能的模型中,最多只有7个可能在超过一半的情况下是正确的。而且,如果任何一个模型碰巧在一半的情况下是正确的,那么与它相反的模型也必定如此。
数据的维数限定了可以创建的模型数量,最多可以有7个模型。我们无法创建出11个独立的模型,更不用说77个了。而且,即使我们有更高维度的数据,比如,假设我们知道贷款者的年龄、平均成绩、收入、婚姻状况和住址,那么依赖这些属性的分类一定能产生准确的预测。每个属性子集都必须与贷款是否已经偿还相关,同时还必须与其他属性无关。这两者都是很强的假设。例如,如果收入、婚姻状况和住址是相互相关的,那么交换这些属性的模型也将是相互相关的。
 在严格的概率模型中,独立性是合理的:不同的模型会产生独立的错误。运用分类模型的原理分析孔多塞陪审团定理的逻辑时,我们看到了构建多个独立模型的困难。
在严格的概率模型中,独立性是合理的:不同的模型会产生独立的错误。运用分类模型的原理分析孔多塞陪审团定理的逻辑时,我们看到了构建多个独立模型的困难。
在试图构建一组多样性的、准确的模型时,也可能会遇到类似的困难。假设我们想要构建一个分类模型来预测500个中型城市的失业率。一个准确的模型必须将这些城市划分为多个类别,以便让同一个类别中的城市具有相似的失业率,而且该模型必须能够准确地预测该类别的失业率。对于两个进行多样性预测的模型来说,它们必须对城市进行不同的分类或给出不同的预测,或两者兼而有之。这两个标准虽然并不冲突,但却很难同时满足。如果一个分类依赖于平均教育水平,而另一个分类依赖于平均收入,那么它们分类的结果可能是类似的。如果确实是这样,这两个模型可能都将是准确的,但却不是多样性的。根据每个城市名称的第一个字母创建26个类别,可以构造多样性的分类,但却很可能无法成为一个准确的模型。最重要的是,在实践中,“许多”实际上可能更接近5,而不是50。
预测的实证研究结果与这种推论一致。虽然增加模型可以提高准确性(根据多样性预测定理,必定会是这样),但是在已经拥有了一定数量的模型之后再继续增加模型,每个模型的边际贡献就会下降。例如,谷歌公司在实践中发现,仅用一位面试官评估求职者(而不是随机挑选),会使录用一名高于平均水平雇员的概率从50%提高到74%,加入第二位面试官可以把这个概率提高到81%,再加入第三位面试官则只能把这个概率进一步提高到84%,加入第四位面试官也只能提高到86%……使用20位面试官也只能将这个概率提高到90%多一点。这些证据表明,增加面试官人数的作用是有限的。
类似的结果也出现在经济学家对失业率、经济增长率和通货膨胀率进行的成千上万次的预测中。在这种情况下,我们应该把每位经济学家视为一个模型。加入一位经济学家会使预测的准确性提高大约8%,加入两位可以提高12%,加入3位可以提高15%,加入10位经济学家则能够将准确率提高大约19%。顺便说一句,假设你知道谁是最好的经济学家,那么最好的经济学家的预测只比平均水平高出大约9%。因此,3位随机选择出来的经济学家的表现就已经优于那位最好的经济学家了。
 相信多位经济学家的平均预测、而不依赖历史上表现最好的经济学家的另一个原因是世界一直在变化。在今天的预测中表现优异的经济学家,明天就可能会泯然众人。同样的逻辑也可以解释为什么美国联邦储备系统要依赖一系列经济模型,而从来不会只依赖某一个经济模型。
相信多位经济学家的平均预测、而不依赖历史上表现最好的经济学家的另一个原因是世界一直在变化。在今天的预测中表现优异的经济学家,明天就可能会泯然众人。同样的逻辑也可以解释为什么美国联邦储备系统要依赖一系列经济模型,而从来不会只依赖某一个经济模型。
这里的教益非常明确:如果能构建出多个多样性的、准确的模型,我们就可以做出准确的预测和估值,并选择正确的行动。这些定理验证了多模型思维逻辑的可靠性。但是,构建出满足这些假设的许多模型,却不是这些定理所能做到的,也不是它们所应该做到的。在实践中,我们可能会发现我们可以构建出3个或5个很不错的模型。如果是这样,那就太好了。我们刚刚讲过,加入1个模型后可以改进8%,加入3个模型后改进幅度可以达到15%。请不要忘记,第二个和第三个模型不一定比第一个模型更好,它们也许会更糟。但是,即使它们的准确性稍差,但只要分类(字面意义)有所不同,就应该把它们加入进来。
许多模型都能在理论上和实践中起到作用,但这并不意味着它们就一定代表正确的方法。有时,我们最好构建一个单一的大型模型。现在,我们就来分析什么情况下应该使用什么策略,同时考虑粒度问题,也就是我们应该在怎样的精细程度上划分数据。
关于应该只用一个大型模型,还是使用多个小型模型的问题,我们先回顾一下模型的7大用途:推理、解释、设计、沟通、行动、预测和探索。其中有4种用途——推理、解释、沟通和探索都要求我们进行简化。通过简化,我们可以应用逻辑来解释现象、交流思想,并探索各种各样的可能性。
回想一下孔多塞陪审团定理。在这个定理中,我们可以分析内在逻辑,解释为什么使用多模型方法更有可能产生正确的结果,也更有利于传播我们的发现。如果我们构建了一个以人格类型分类的陪审员模型,并将证据描述为语词的载体,我们就会迷失在细节的丛林中。阿根廷著名作家豪尔赫·路易斯·博尔赫斯(Jorges Luis Borges)在一篇科学论文中阐明了这一点。他描述了一批总想制作更精细地图的制图师:“制图师协会决定制作一幅国家地图,它的大小与国家大小相同,而且一对一地将土地上的每一点都标记在地图上。但是,他们的后代不像他们的祖先这样喜欢研究制图,并认为这种巨大的地图毫无用处。”
模型的另外3种用途——预测、设计和行动,却可以因高保真模型而受益。因此,如果有大数据,那么就应该利用它。根据经验,我们拥有的数据越多,模型就越精细。这一点可以通过用来梳理思维的分类模型来说明。假设我们想构建一个模型来解释数据集中的变化。为了给问题提供一个背景,不妨再假设我们从很多杂货店获取了大量数据,详细列出了数百万家庭每个月的食品支出。这些家庭的消费金额不同,我们用变差(variation)来衡量这种变化,也就是每个家庭的支出与所有家庭的平均支出之间的差的平方和。如果每个月的平均支出是500美元,而某个特定家庭每个月的支出为520美元,那么这个家庭对总变差(total variation)的“贡献”就是400(20 2 )。统计学家把一个模型中能够解释的变差比例称为该模型的 R 2 。
如果数据的总变差为10亿,而模型解释了其中的8亿,那么这个模型的 R 2 是0.8。解释的变差比例对应于模型在平均估计上的改进程度。如果某个模型估计某家庭每个月的支出为600美元,而且这个家庭的实际支出确实为每个月600美元,那么这个模型就解释了该家庭对总变差的全部贡献。如果家庭支出为800美元,但是模型的预测是700美元,那么对总变差的贡献就从原来的9万[(800-500) 2 ],变成了1万[(800-700) 2 ]。从而模型解释了8/9的变差。
R 2 :解释变差的百分比
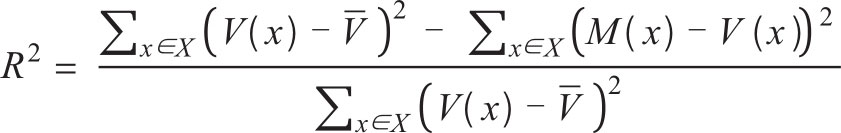
其中,
V
(
x
)等于
X
中的
x
的值,
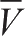 等于平均值,
M
(
x
)等于模型的估值。
等于平均值,
M
(
x
)等于模型的估值。
在这种情况下,分类模型将家庭划分为不同类别,并估计了每个类别的值。更精细的模型会创建更多的类别,而要创建这些类别就需要更多的家庭属性。如果加入了更多的类别,可以解释的变差比例就会更大。如果我们像博尔赫斯所说的那些制图师一样思考,将每个家庭都分为一类,我们就可以解释所有的变差。但是,这种解释,就像比例为1:1的地图一样,没有多大用处。
创造过多的类别会导致对数据的过度拟合,而过度拟合会破坏对未来事件的预测。假设我们想利用上个月的食品采购数据来预测本月的数据,而家庭每月的支出是会有变化的。如果一个模型将每个家庭都分为一类,那么就可以预测家庭的支出与上个月相同。由于存在月度波动,这个模型并不是一个好的预测器。通过将某个家庭与其他类似的家庭归入同一个类别中,我们可以通过对类似家庭在食品上的平均支出来构建一个更准确的预测器。
为此,我们假设每个家庭的月支出是从某个分布中抽取出来的(我们将在第5章详细讨论各种分布),再假设分布的均值和方差已知。创建分类模型的目的是根据属性构建类别,使同一类别中的家庭具有类似的均值。如果能做到这一点,那么某个家庭在第一个月内的消费就能够告诉我们其他家庭在第二个月的支出大概是多少。当然,没有任何一种分类方法是完美的。在每个类别中,家庭的均值可能会略有不同,我们称这种情况称为分类误差(categorization error)。
构建的类别越大,分类误差就越大,因为类别越大,我们就越可能将具有不同均值的家庭集中到同一个类别中。但是,更大的类别依赖更多的数据,又可以使我们对每个类别均值的估计更加准确(参见第5章中讨论的平方根规则)。因估计均值错误而出现的误差称为估值误差(valuation error)。估值误差随类别数量的增加而减少。如果不同家庭的月支出不同,那么包含一个家庭的类别(甚至包含10个家庭的类别也一样)将无法准确估计均值,但包含1 000个家庭的类别则能够准确地估计均值。
现在,我们已经得到了关键的直觉:增加类别的数量能够通过将具有不同均值的家庭归入同一个类别减少分类误差。统计学家将这种情况称为模型偏差(model bias)。但是同时,构建更多类别则会增加对每个类别均值估计的误差,统计学家将这种情况称为均值方差的增加。因此,我们在决定要构建许多个类别时就面临着一个权衡。对于这种权衡,我们将它总结为模型误差分解定理(model error decomposition theorem),统计学家则将这个结果称为偏差-方差权衡(bias-variance trade-off)。
模型误差分解定理
偏差-方差权衡
模型误差=分类误差+估值误差
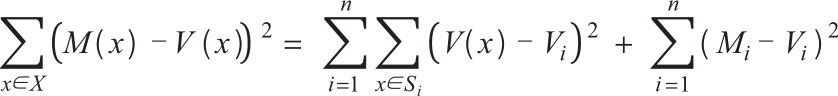
其中, M ( x )和 M i 分别表示数据点 x 和类别 S i 和 V ( x )的模型值, V i 表示它们的实际值。 1
学习模型需要时间精力以及广泛的兴趣和知识。为了减少学习成本,我们可以采用一对多的方法。我们提倡掌握适量的、比较灵活的模型,并学会创造性地应用它们。例如,我们可以使用流行病学模型来解释玉米良种的扩散、Facebook的风行、犯罪行为的传播和流行明星的“吸粉”。我们将信号传递模型应用于对广告、婚姻、孔雀羽毛和保险费的分析。我们利用进化适应的崎岖景观模型解释为什么人类不需要鲸鱼那样的喷气孔。当然,我们不能随便拿起一个模型就将它应用到任何情境之中。但是,大多数模型都是灵活的。而且,即使失败了我们也会有所获益,因为尝试创造性地使用模型能够暴露它们的局限,这是一件很有趣的事情。
一对多方法是一个相对较新的方法。过去,特定的模型只属于特定的学科。经济学家有供求模型、垄断竞争模型和经济增长模型;政治学家有选举竞争模型;生态学家有关于物种形成和复制的模型;物理学家有描述运动规律的模型,等等。所有这些模型都是针对特定目的而构建的。那个时候,科学家们不会将物理模型应用到经济学领域,也不会用经济学模型去研究大脑,就像普通人不会用缝纫机来修理泄漏的水管一样。
但是今天,将模型从各自所属的学科孤岛中“释放”出来,并将它们以一对多的方法应用到其他领域中去的做法已经取得了显著成功。经济学家保罗·萨缪尔森(Paul Samuelson)重新诠释了物理学中的模型,以解释市场如何实现均衡。经济学家安东尼·唐斯(Anthony Downs)利用经济学中描述海滩上冰激凌商店之间的竞争的模型,解释了相互竞争的政治候选人在意识形态空间上的定位。社会学家应用粒子相互作用的模型,分析不同国家的贫困陷阱、犯罪率的变化,甚至经济增长。经济学家则已经开始采用基于经济原理的自我控制模型来理解大脑的功能。

要想创造性地应用模型,需要不断实践。为了说明“一对多”这种方法的巨大潜力,在这里以一个大家熟悉的数学公式 X N ,也就是求一个变量的 N 次方为例,并将它作为模型应用。当幂等于2时,这个公式给出的是正方形的面积;当幂等于3时,它给出的是立方体的体积。当幂变为更高的值时,这个公式则刻画了几何膨胀或几何衰减。
超级油轮: 第一个应用是考虑一艘长方体状的超级油轮,其长度是深度和宽度的8倍,表示为 S 。如图3-1所示,超级油轮的表面积为34 S 2 ,体积则为8 S 3 。建造一艘超级油轮的成本主要取决于它的表面积,因为这决定了所需钢材的数量。而超级油轮能够产生的收入数量则取决于它的体积。先计算一下体积与表面积之比,为8 S 3 /34 S 2 ≈ S /4,这表明,随着尺寸的增加,盈利能力呈线性增长。
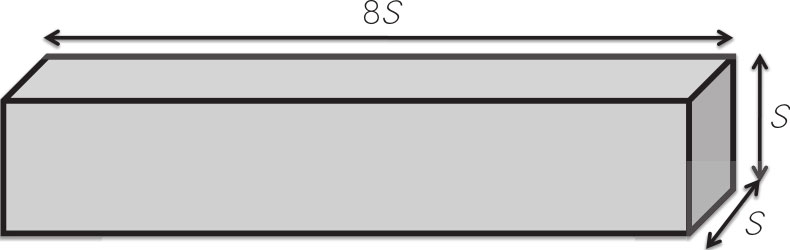
图3-1 长方体状的超级油轮:表面积=34S 2 ,体积=8S 3
航运业巨头斯塔夫罗斯·尼阿科斯(Stavros Niarchos)掌握了这个比例关系,他建造了第一艘现代超级油轮,并在第二次世界大战后的重建期间赚了数十亿美元。第二次世界大战期间使用的T2油轮长152米、深7米多、宽15米多。而现代超级油轮,例如诺克·耐维斯号(Knock Nevis),则长450多米、深20多米、宽50多米。要想象诺克·耐维斯号这样超级油轮的大小,不妨想象一下,将芝加哥的西尔斯大厦放倒,并让它漂浮在密歇根湖的水面上会是什么样子。诺克·耐维斯号大体上相当于将T2油轮放大了3倍多。然而,与T2油轮相比,诺克·耐维斯号的表面积是T2邮轮的10倍,体积则是T2邮轮的30倍。有人也许会问,那么为什么超级油轮不造得更大一些呢。答案很简单:超级邮轮必须通过苏伊士运河。事实上,诺克·耐维斯号每一次通过苏伊士运河时,都是“挤”过去的,它的两侧都只能剩下一点儿缝隙。

身体质量指数: 医学界通常用身体质量指数(BMI)来定义身体质量的不同类别。身体质量指数最早出现在英国,计算方法是一个人的体重与身高的平方比。 2 因此,保持身高不变,身体质量指数会随体重呈线性增长。如果一个人比身高相同的另一个人重20%,那第一个人的身体质量指数就会高出20%。
为了应用模型,我们先将人假设为近似一个完美的立方体,由脂肪、肌肉和骨骼的某种混合物构成。 M 表示1立方米立方体的重量。那么“人体立方体”的重量就等于它的体积乘以每立方米的重量,即 H 3 × M ,立方体的“身体质量指数”就等于 H × M 。到这里,这个模型还有两个缺陷:身体质量指数随身高呈线性增长;而且考虑到肌肉比脂肪更重,更健美的人会有更高的 M ,因此会有更高的身体质量指数。身高本应与肥胖无关,而肌肉发达本应是肥胖的对立面。即便我们使这个模型变得更加“真实”,这些缺陷仍然存在。
如果使用参数
d
和
w
来表示一个人的“深度”(前胸到后背的厚度)和“宽度”,并与高度成比例,那么身体质量指数可以写成:
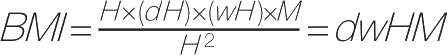 。这样一来,许多NBA以及其他球类运动明星的身体质量指数将会把他们归入超重类别(BMI>25),甚至许多世界顶尖男子十项全能运动员也不能幸免于难。
。这样一来,许多NBA以及其他球类运动明星的身体质量指数将会把他们归入超重类别(BMI>25),甚至许多世界顶尖男子十项全能运动员也不能幸免于难。
 由于即便是身材适中、身体健康的人也可能有很高的身体质量指数,我们不应该对如下结果感到惊讶:对涉及样本总数高达数百万人的近百项研究进行的一个荟萃分析表明,体重稍稍超标的人寿命更长。
由于即便是身材适中、身体健康的人也可能有很高的身体质量指数,我们不应该对如下结果感到惊讶:对涉及样本总数高达数百万人的近百项研究进行的一个荟萃分析表明,体重稍稍超标的人寿命更长。

代谢率: 现在,应用模型来预测动物大小与代谢率之间的反比关系。每个生物体都要进行新陈代谢,也就是重复进行的一系列化学反应,分解有机物质并将之转化为能量。以卡路里计量的生物体代谢率等于维持生命所需的能量。如果我们构建小鼠和大象的立方米模型,那么从图3-2可知,小立方体的表面积与体积的比值要大得多。
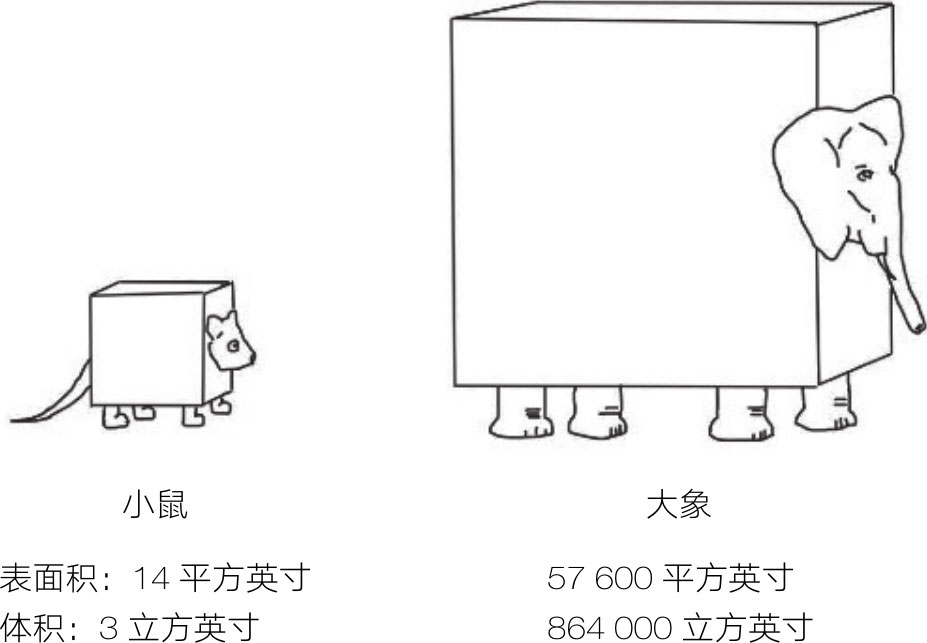
图3-2 膨胀的大象
我们可以把小鼠和大象建模为:身体由1立方英寸体积大小的细胞组成,每个细胞都进行新陈代谢,同时这些代谢反应产生的热量必须通过动物的体表皮肤发散掉。小鼠的表面积为14平方英寸,体积为3立方英寸,表面与体积之比约为5:1。
 因而,对小鼠来说,每立方英寸的细胞,就有5平方英寸的体表皮肤来散热。相比之下,大象的每个发热细胞则仅有1/15平方英寸的体表皮肤来散热。这就是说,小鼠散热的速度是大象的75倍。
因而,对小鼠来说,每立方英寸的细胞,就有5平方英寸的体表皮肤来散热。相比之下,大象的每个发热细胞则仅有1/15平方英寸的体表皮肤来散热。这就是说,小鼠散热的速度是大象的75倍。
因此,对于这两种动物来说,要想保持相同的体内温度,大象的新陈代谢就必须更慢。事实也确实如此。如果一头大象的新陈代谢速度与小鼠一样,那么这头大象每天将会需要吃下6 800千克的食物。那样的话,大象的细胞所产生的大量热量无法完全通过它的体表皮肤发散出去。最后,大象将会热到冒烟,然后爆炸。在现实世界中,大象之所以没有爆炸,原因就在于它们的代谢率为小鼠的1/20。这个模型不能预测新陈代谢随体形大小而变化的速度,但是准确地预测了方向。更精细的模型还可以解释比例定律。

女性CEO: 最后,我们进一步增大公式中的指数,并以此来解释为什么只有较少的女性能够成为CEO。根据统计,2016年,只有不到5%的财富500强企业是由女性CEO掌管的。一个人要成为一名CEO,必须经历多次升职。我们可以将这些升职机会建模为概率事件,即一个人有一定概率可以升职。然后进一步假设,要成为CEO,必须做到每一个升职机会都不会错过。
我们假设,要成为一名CEO,至少要升职15次,这大体上相当于每两年升职一次、在30年内成为CEO。大量证据表明,升职时会出现有利于男性的“温和”的偏差。我们可以将这种偏差建模为男性升职的概率更高一些。
 具体地说就是将这种偏差描述为男性的升职概率略高于女性的升职概率。如果将这两个概率分别设定为50%和40%,那么男性最终成为CEO的可能性几乎是女性的30倍!
3
这个模型揭示了“温和”的偏差会累积成为非常巨大的差异。10%的升职概率差异,最终变成了成为CEO可能性的30倍的差距。
具体地说就是将这种偏差描述为男性的升职概率略高于女性的升职概率。如果将这两个概率分别设定为50%和40%,那么男性最终成为CEO的可能性几乎是女性的30倍!
3
这个模型揭示了“温和”的偏差会累积成为非常巨大的差异。10%的升职概率差异,最终变成了成为CEO可能性的30倍的差距。
这个模型也可以为如下现象提供一个新的解释:为什么女性大学校长的比例(大约25%)要比女性CEO的比例高得多?与财富500强企业相比,学院和大学的管理层级较少。一名教授只需升职3次,就可以成为大学校长:系主任、院长,然后就是校长。既然只有3个层级,那么偏差累积的程度就不会太过严重。因此,女性大学校长的比例更高,并不意味着教育机构比企业更加平等。
在本章的一开始,我们通过孔多塞陪审团定理和多样性预测定理为多对一的方法奠定了逻辑基础。然后,我们使用分类模型说明了模型多样性的局限性,也阐述了多个模型是怎样改进我们在预测、行动和设计等方面的能力的,同时也指出,要想构建多个不同的模型并不容易。如果可以的话,也就能达到接近完美的预测准确度了,但是我们很清楚这是不可能的。无论如何,我们的目标是尽可能多地构建有用的、多样性的模型。
在接下来的各章中,我们将会描述一系列核心模型。这些模型突出了世界的不同部分,它们对因果关系做出了不同的假设。通过它们的多样性,这些模型创造了多模型思维的可能性。通过强调更复杂整体的不同部分,每个模型都可以发挥自己的作用,还可以成为更强大的模型集合的一部分。
如前所述,多模型思维确实要求我们掌握多个模型,但是我们并不需要懂得非常大量的模型,只需要知道每个模型都可以应用到多个领域,但这并不容易。成功的一对多思维取决于创造性地调整假设和构建新的类比,以便将为某个特定目的而开发的模型应用到新的领域。因此,要成为一个多模型思考者,需要的不仅仅是数学能力,更需要的是创造力。这一点我们已经看得很清楚了。
通常,我们会用模型与现有数据集中的样本拟合,然后用其余数据来检验这个模型。而在其他一些时候,我们会用模型去拟合现有数据集,然后用该模型去预测未来的数据。然而,这种构建模型的过程会产生一种张力:模型中包含的参数越多,就越能够很好地拟合数据,同时也越有可能过度拟合。好的拟合不一定意味着好的模型。
物理学家弗里曼·戴森(Freeman Dyson)曾经谈到物理学家恩利克·费米(Enrico Fermi)对他的一项研究的评论。那项研究的模型拟合度极高。“无奈之下,我问费米是不是对我们计算出来的数值与他测量出来的数值之间的高度一致性没有什么印象。他反过来问我:‘你是用多少个任意参数进行计算的?’我回忆了一下我们的截止程序,然后告诉他‘4个’。他说:‘我记得我的朋友约翰·冯·诺伊曼曾经说过,有4个参数,就可以拟合一头大象;有5个参数,就可以让大象摆动它的大鼻子了。’然后,对话就结束了。”

用于“摆动大象鼻子”的估计量通常包括了更高阶的项:平方、立方,甚至四次方。高阶项的存在会带来大误差的风险,因为高阶项有很强的放大效应。10只是5的两倍,但是10 4 却是5 4 的16倍。下图显示了过度拟合的一个例子。
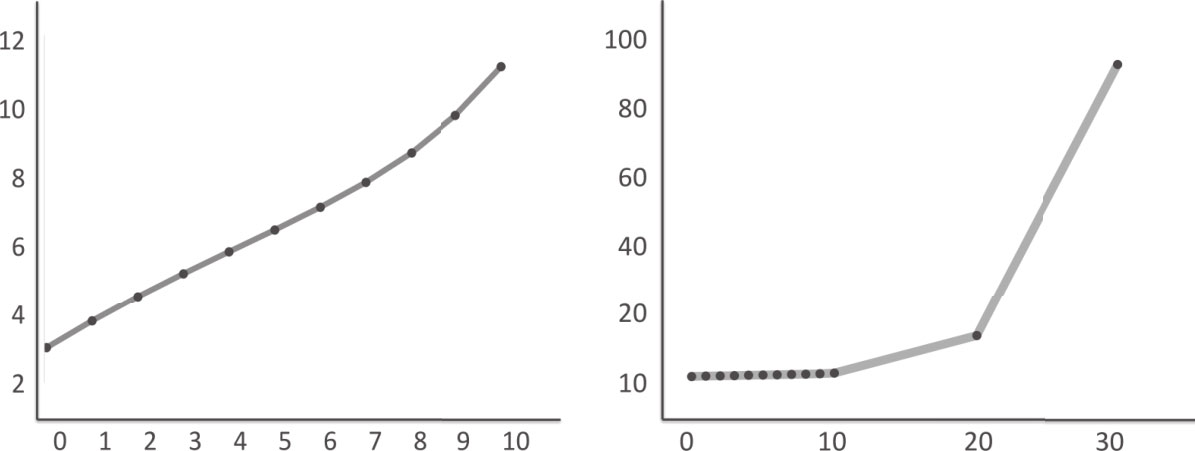
过度拟合与样本外误差
左图显示了一家生产工业用3D打印机的企业销售数据(假设),销售数据是该公司的销售团队每月(平均)上门推销次数的函数。左图显示的是一个非线性最优拟合,包括非线性项的5次方。右图则表明,如果销售团队上门推销的次数达到了30,那么该模型预测3D打印机的销售量将达到100台。如果一个客户最多只购买一台3D打印机,那这个预测就不可能是正确的。因此,由于存在过度拟合,这个模型出现了巨大的样本外误差。
为了避免过度拟合,可以避免使用高阶项。不过,一种更巧妙的解决方法是,可以采取自举聚合法(bootstrap aggregating)或装袋法(bagging)来构建模型。为了引导数据集,我们从原始数据中随机抽取若干数据点,创建多个规模相同的数据集。抽取这些数据点时,采取的是抽出后放回的方法,也就是说,在抽取了一个数据点之后,我们又将它放回到“袋子”中,下一次仍然可能会抽到它。这种技术产生了一组规模相同的数据集,每个数据集都包含某些数据点的多个副本而不包含其他数据点的副本。
然后,我们将(非线性)模型拟合到每个数据集上,以便生成多个模型。
 这样一来,就可以把所有数据集都绘制在同一组数轴上,从而得到一幅如下所示的“意大利面图”(spaghetti graph),图中颜色最深的那条线表示不同模型的平均值。
这样一来,就可以把所有数据集都绘制在同一组数轴上,从而得到一幅如下所示的“意大利面图”(spaghetti graph),图中颜色最深的那条线表示不同模型的平均值。
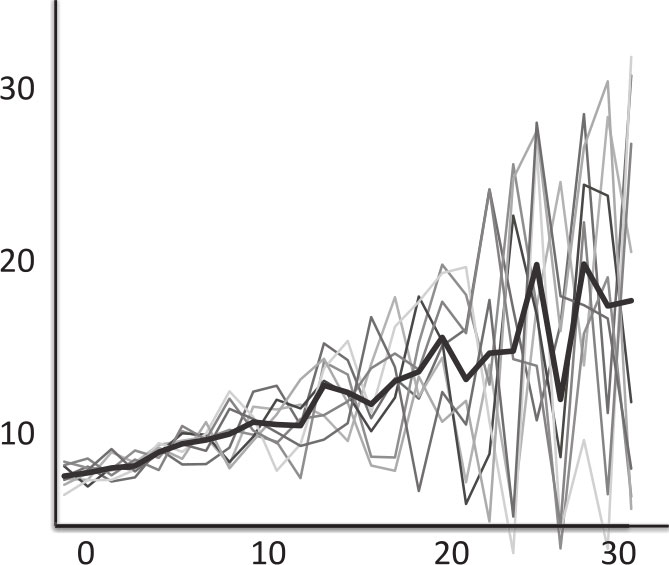
意大利面图
装袋法能够刻画鲁棒的非线性效应,因为它们在数据的多个随机样本中都清晰可见,同时又能避免在任何单个数据集中去拟合特殊模式。通过随机样本构建多样性,然后对多个模型求平均值,装袋法很好地应用了多样性预测定理背后的逻辑。它构建了多样性的模型,如前所述,这些模型的平均值将比模型本身更加准确。