下载掌阅APP，畅读海量书库
立即打开
《九章算术》（以下亦称《九章》）是国际学术界早已公认的中国古代东方数学的代表作，古今中外对这一历来被视为“算经之首”的数学典籍的学习与探讨是数学史研究的永恒话题。
早在20世纪三十年代，日本著名数学与数学史家藤原松三郎就曾在一次关于“东洋数学史”的学术演讲中，发表过极为精辟的见解：研究东洋数学史，首先要研究中国数学的发展史；而要研究中国数学史，则必须从研读《九章算术》开始。
19世纪八十年代，英国科学技术史专家李约瑟（Joseph Terence Montgomery Needham）在他的《中国科学技术史》这部巨著的篇首中写道：至于远东的文明、特别是其中最古老而又最重要的中国文明对科学、科学思想和技术的贡献，直到今天还仍然为云翳所遮蔽，而没有被人们所认识。“远东”这个名词本身，就说明了欧洲人有一种根深蒂固的偏见，甚至连那些怀有良好意愿的欧洲人，也很难排除这种偏见。
我国著名数学家吴文俊先生在1990年发表的《关于研究数学在中国的历史与现状》中预言道：《九章》与“刘注”所贯串的机械化思想，不仅曾经深刻影响了数学的历史进程，而且对数学的现状也正在发扬它日益显著的影响。它在进入21世纪后在数学中的地位，几乎可以预卜。
《九章算术》与《几何原本》是大约同一时代的东、西方数学成就的总结。早在七八十年以前，日本数学史家小仓金之助就把《九章算术》与《几何原本》（以下亦称《原本》）相提并论，认为《九章》是“中国的欧几里得”。
作为古代东、西方数学的代表作，《九章》与《原本》在数学发展史上的产生与流传确有许多相似之处。
然而当人们把中国古代科技发展的史实与近代科学的产生相联系而思索时，便萌生了一个使人困惑不解的问题：近代自然科学为何不发生在中国？这就是举世瞩目的“李约瑟难题”。为寻求问题的答案，一种似是而非的推论颇为流行：近代自然科学未能发生在中国，是因为中国传统数学没有发展成近代数学；中国古代传统数学未能发展成近代数学，乃是由于中国传统数学本身的弱点所决定的。
所谓中国传统数学的弱点，质言之即指中国古代数学没有形成如同古希腊数学那样的公理化演绎体系。长期以来，西方学者视古希腊学术为人类科学及科学思想的根源。欧几里得的《几何原本》被奉为几何学的“圣经”；为《几何原本》所建立的由定义、公理、定理、证明构成的演绎系统，成为近代数学推理论证的典范。尤其从20世纪三十年代始法国的布尔巴基（Bourbaki）学派提出了用结构这一概念来贯串整个数学，并以其鸿篇巨制《数学原理》对数学发展产生了巨大影响。直至“李约瑟难题”提出的20世纪五十年代，布尔巴基的影响已波及整个数学界。在当时的历史条件下，以西方数学公理化体系为“标准”去评判中国传统数学的短长，从中找出某些“弱点”与“缺陷”，用以论证中国传统数学之所以未能发展为近代数学的原因是不足为怪的。这种“拘泥于西方数学的先入之见”的论证，自然最终无法摆脱“西方中心论”的偏见。
关于“东方数学的算法体系”的观点之提出，是近年来中国数学史研究的重大成就；与此相应，人们对于公理化体系与方法的意义与局限性，也开始了冷静的思索。
由《九章算术》研究而引起的对古代东、西方数学体系的比较，是一个极有意义的论题。事实上，在整个数学科学发展的历程中，始终存在着算法与演绎两种倾向，它们代表着东、西方数学传统的基本特征。回溯数学发展的历史，我们就会发现：数学的发展并非始终是演绎倾向独霸天下，而总是算法倾向与演绎倾向交替取得主导地位。古代巴比伦和埃及式的原始算法，被希腊式的演绎几何所接替；而在中世纪希腊数学衰落之时，算法倾向在中国、印度等地区继续繁荣，以至17、18世纪在欧洲产生无穷小算法时期；19世纪以来，随着分析的严格化运动，演绎倾向再度兴起，它在比古希腊高得多的水准上远远超越几何学的范围而扩展到数学的其他领域，成为现代数学的中流砥柱。
吴文俊先生在《关于研究数学在中国的历史与现状》中总结道：“世界古代数学分为东、西方两大流派。古代西方数学是以古希腊欧几里得《几何原本》为典范的公理化演绎体系；古代东方数学则是以我国《九章》及其刘徽注为代表的机械化算法体系。在世界数学发展的历史长河中，这两种体系互为消长，交替成为主流，推动着这门学科不断向前进展。”
20世纪中叶以来，随着电子计算机的出现，计算技术不仅在社会生活中的作用显著提高，也使数学的发展产生了根本性变革，与公理化演绎体系大相径庭的机械化算法体系随之兴起，它已越来越为数学家所认识和重视。当人们开始注意算法史的研究之时，数学史家才深刻地认识到，那种肇始于古代中国而不同于古希腊传统的东方数学，正是典型的机械化算法体系。以《九章算术》为代表的机械化算法体系，在经过明代以来近几百年的相对消沉之后，由于电子计算机的兴起而重新活跃起来。近年来，不少著名的数学家纷纷转向计算机代数、计算性几何一类新兴学科。一个令人惊喜的成就是几何定理证明的机械化。20世纪七十年代末期，著名数学家吴文俊先生从中国数学史研究领域转入数学机械化领域，在短短的几年间便获得了突破性进展。他所创立的机器证明理论在国际上被誉为“吴方法”，不仅被成功地应用于初等几何、微分几何、非欧几何等领域，而且迄今已证明了大量的数学定理，并使自动推理研究应用于高科技的诸多领域。追溯这一方法的来源，吴文俊解释说：“（它）直接导源于我国传统数学的思维方式，也就是从公元前1世纪成型的《九章算术》开始经祖冲之到元代大数学家朱世杰形成的以解方程为特色的机械算法体系。”
另一重要的《九章》史实表明，作为近代数学主要标志的微积分学，并非希腊演绎数学传统的发展，而是东方算法传统胜利的产物。东方数学的算法精神早在文艺复兴时期前就通过阿拉伯人传播到欧洲，并为欧洲学者所吸收。微积分学的发展史表明，从16世纪中期开始的一百多年间，为解决力学与几何学等领域提出的一系列实际问题，许多大数学家都致力于寻求这种特殊的“无穷小算法”，而并不注意算法的证明。这种倾向一直延续到18世纪末。“极限的概念，作为微分学的真正基础，对于希腊头脑来说完全像是一个外国人。”
然而，极限的方法作为中算传统数量观与数系理论的自然发展，早已为刘徽在圆面积与角锥体积计算中成功地运用。
在微积分的创造过程中起着重大作用而为西方学者盛称的所谓卡瓦列里（Cavalieri）原理，事实上早已为古代中算家所应用并为刘徽、祖暅成功地应用于球积计算，它于中算当称之为“刘祖原理”。中国古代数学的研究证明，我国古代早已“具备了西欧17世纪发明微积分前夕的许多条件，不妨说我们已经接近了微积分的大门”
。
研究数学史的目的在于“古为今用”“以史为鉴”。用现代数学的观点研究《九章算术》始于20世纪初。对《九章》的早期研究，主要是日本数学史家三上义夫
（1875—1950）、小仓金之助
（1885—1962），美国数学史家D. E.史密斯
（D. E. Smith, 1860—1944）及F.卡约黎（F. Cajori, 1859-1930）
，我国数学史家李俨
（1892—1963）、钱宝琮
（1892—1974）等人的工作，当以中日学者的贡献称著。20世纪五十年代以后，苏联与东欧各国对《九章算术》及刘徽注的研究得以展开。A. Л.尤什凯维奇（A.л.ющкeвиц）
和Э. И.别辽兹金娜（Э. И.Ьepeзкинa）
等苏联数学史家的工作占据着显要的地位。与此同时，美国与西欧对《九章》与“刘注”的研究亦日趋深入。英国科学史家李约瑟
（1900—1995）和他的合作者王铃
（1917—1994）是其中的杰出人物。李约瑟的《中国科学技术史》的数学章，是当时西方世界中唯一的一本系统论述中国古代数学的专册。对中国古代数学的成就及其在世界数学史上的地位做出较为客观公允的评述。书中列举了十进位位值制记数法、圆周率计算、贾宪三角形与高次数字方程求根法等中算家的卓越成就，来说明在宋元时期以前中国人在数学的许多领域处于领先于欧洲的地位。另外，西方学者在某些方面也取得了值得称赞的成就。丹麦学者华道安（D. B. Wagner）关于“刘徽阳马术注”和“刘徽、祖暅之论球积”的研究
，就是其中显著的例证。
特别值得注意的是20世纪后半期以来，《九章算术》先后被译成多种文字出版。继1956年王铃将《九章算术》译为英文之后，1957年Э.И.别辽兹金娜将它译成了俄文，1968年K. Vogel把《九章算术》译为德文，1975年大矢真一与清水达雄各自发表了《九章》的日文译本。但遗憾的是上述各译本都未翻译刘徽的注释。1978年日本的朝日新闻社出版的《科学名著》第二册《中国天文学·数学集》收入了川原秀成所译的《九章算术》日文版，它是首个包括刘徽注在内的完整的《九章算术》的外文译本。（另有1999年出版的沈康身的英文译本，2004年出版的林力娜（Karine Chemla）的法文译本。）
对比近代关于《九章》与《原本》的研究进程，无疑《九章》的研究起步较晚，亦不如《原本》研究之广泛、深入。然而20世纪七十年代后期兴起的“《九章》热”，却大有后来居上之势。由于现代计算机所需数学的方式方法，正与《九章》传统的算法体系若合符节，因此《九章》的研究更加具有重大的现实意义。《九章算术》内容博大精深，与《几何原本》相比确有许多优胜之处。“若把《原本》比《算数》，此中翘楚是《九章》。”
任何一个民族的科学文化都有其发生发展的历史渊源，因而表现出迥然不同的风格与特色。数学在古希腊哲学体系中占有重要的地位。古希腊的哲学具有重视抽象、崇尚逻辑、追求理想的传统。受这种传统思想的影响，古希腊的数学家尤其注重数学的推理论证，追求理论的系统完美。于是自然形成了其数学研究的传统：一切数学结论必须根据明确规定的公理以无懈可击的演绎法推导出来。经过几代数学家的努力，最终由欧几里得《几何原本》的公理化体系构建了西方数学理论的“范式”。着重抽象概念与逻辑思维，以及概念与概念之间的逻辑关系，以定义、公理、定理、证明构成其表达形式。与古希腊形成鲜明的对照，中国先秦诸子的思想则多具有注重实践、推崇经验、讲求实用的倾向。无论是儒家内在的人文主义还是道家传统的自然主义，虽然也具有思辩性与逻辑性，但它更偏重于直觉和经验的因素。对中国古代数学有深刻影响的墨家学说，它一方面促进了数学逻辑因素的发展，另一方面墨家所代表的手工艺者阶层注重生产实践的思想体系也会带来数学技术化的倾向。法家管仲把“计数”列为他的“七法”之一，强调计算与数学对于社会生活的重要性，其着眼点也在于把它看作是成就任何一件大事的必要手段。如此的先秦时期思想与文化形成了中算家的科学传统：从各个不同的实际应用领域中抽象出具有普遍意义的数学问题与模型，经过分析提高而提炼出一般的原理、原则与方法，运用这些基本的数学原理构造其求解的简捷而能行的机械化算法。与这一独特的算法体系相适应，我国传统数学乃是由问、答、术、注、草等几个彼此相关联的项目构成其独特的表达形式。《九章算术》表达的这种数学机械化算法体系，可以说是与《几何原本》异其旨趣的东方数学理论的“范式”，形成了欧几里得《几何原本》纯粹数学的公理化体系与中国古代《九章算术》应用数学的机械化算法体系的鲜明对比。
（一）篇章结构与理论系统
《九章算术》是以应用问题解法集成的体例编纂成书的。全书246个题目按其应用范围与解题方法划分为九章，按应用领域来分科，具有浓厚的“应用数学”的色彩。《九章》中的每一类题目之下又包含着若干条目的内容。《九章》本文一般由三部分组成：一是“问”；二是“答”；三是“术”。除本经之外，传本还有后世学者的注释。在《九章》以后的历代算经大都遵循它的这种体例，有的还增加了演草、比类、演段等项目。
作为《九章》篇章名称的方田、粟米、衰分、少广、商功、均输、盈不足、方程、勾股，代表了中国传统数学的分科。它肇源于古老的《周礼》“九数”，这与汉末郑玄《周礼注》之说相合：“九数：方田、粟米、差分、商功、均输、方程、赢不足、旁要；今有重差、勾股。”“方田”，以御田畴界域，即是应用于田亩地域大小丈量的数学分科，大致是最初的测地学。“粟米”，以御交质变易，即是应用于谷物之类商品交易的数学分科，当属古代的商业数学。“衰分”，以御贵贱禀税，即是应用于粮食、税收等经济管理部门的数学分科，当属古代的经济数学。“少广”，以御积幂方圆，是处理几何学中面积与体积类问题的计算，广泛应用于多种学科，如测地学。“商功”，以御功程积实，即是应用于工程管理部门的数学分科，当属古代的工程数学。“均输”，以御远近劳费，即是应用于赋税徭役摊派方面的数学分科，当属古代的管理数学。“盈不足”，以御隐杂互见，是一种线性插值算法，通过两次假设获得的数据，求取两个未知量。“方程”，以御错糅正负，它是由“程禾”发展而来，即是应用于谷物测产方面的数学分科，似乎属于古代的农用数学了。至于“勾股”，以御高深广远，它是由古老的旁要发展而来；旁要，从旁腰取，即是应用于布点测量的数学分科，也就是古代的测量学了。
然而，按应用领域分科并不意味着这种数学就没有理论系统，《九章算术》便具有其内在独特的理论结构。其特点就在于它是以基本的算法与数学模型为其理论构成单位；而这各种各样的算法又以为数不多的基本原理或法则为“纲纪”，贯串成一个完整的算法理论体系。
《九章》全书246问分属于53种算法。其实，《九章》的章名亦是一种基本算法的名称。
方田章主要讲各种图形面积的计算，它以方田即直田面积算法为基础，采用割邪补直、化圆为方、以直代曲等直观性方法，将各种图形化为方田算得其面积的精确或近似数值。因此方田术即为本章的基本算法。由于度量精密化的要求而产生的分数算法，也作为一个完整的数学基本内容附置于全书的首章之中。
粟米章的基础为“粟米之法”，即依各种谷物的交换率而相互推求的比例算法，古称“今有术”。由此引导出计算物品单价的经率术；进而讨论单价的近似整值与贵贱物价的分配，发展出颇为独特的其率术与反其率术。
衰分，即按比例分配，它是古代应用相当广泛的基本算法。衰分讨论成正比关系的量，而返衰则讨论成反比关系的量。在衰分章中化返衰为列衰，即将正、反比关系统一处理，两者化归同一算法。
少广章讨论的问题与方田章相逆，即由已知面积反求边长或周长。由正方形面积求边，由圆（球）之积求周（径），则为开平方或开立方算法。开方本于除法，它是除数待定条件下的除法。少广即是由除法到开方的运算理论。
商功是讨论各种柱、锥、台体的求积，其中心是阳马术（即四棱锥体积计算），它奠定了中算家多面体体积理论的基础。
均输术是由正、反比关系复合而成分配问题之解法，它作为衰分术之发展而广泛用于徭役分配与调节运输。
盈不足章讲双假设法及其实际应用，它最终归结为“盈不足”“两盈、两不足”“盈适足、不足适足”三种模式的计算。
“方程”术相当现今线性方程组的矩阵解法，其中行列相加减自然地推广到正负数的范围。
勾股章的前部分是讲解勾股形的各种算法，它是其后部分勾股测量的理论根据。
《九章》的数学体系表现为算法的集合，这些算法前后关联、井然有序，反映出算法理论发展的来龙去脉。如果将《原本》的理论结构称做“逻辑链”的话，那么《九章》的理论结构当称之为“算法链”。自然“逻辑链”前因后果关系显然；而“算法链”的联结纽带却很隐蔽。联结“算法链”的纽带主要是数学的基本原理与法则，即“算之纲纪”；贯穿《九章》各部分算法的一条总纲便是率的运算法则。
“凡数相与者谓之率。”比率是古代算家最常见的数量关系。用以表示一组比率的数可以“粗者俱粗，细者俱细”，从而可以“乘以散之，约以聚之，齐同以通之”。比率的这种基本运算性质被中算家化为筹式的演算规则，成了贯串《九章》算法理论的一条总的纲纪。
《九章》中形形色色的数学应用问题都可以通过分析其中数量间的比率关系，最终用“今有术”，即四项比例算法求得问题的解答。《九章》中所建立的列衰、返衰、均输、盈朒、方程等各种筹算模式，皆以比率关系为基础。《九章》中数与式的演算差不多都可以归结为比率的遍乘、通约与齐同。在古代算家对于数量关系，即“势”的认识中，把比率看成一切。正如《九章算术》所反映出来的，宇宙之内，天地人物，似乎无一不是比率关系：天圆地方，而圆、方以三、四为率；物物交换，以率相通；得禄出税，依爵次衰分，而列衰，相与率也；徭役摊派，均而输之，而均输者，以行道日约户数为衰，乃衰分之别术也；形与形间，以率相关，圆台之于方台，圆方之率也；“丸居立方，十六分之九也”。凡此种种，天地、人际、物际、形际之间，“其相与之势”（即关系）无一不可用率来表示。虽然在《九章算术》“盈不足”章中，中算家已经遇到了数量间更为复杂的（高次与超越）“关系”，但是他们都毫不例外地将其当作比率关系而用盈不足术去处理。即使对几何量的考察也以比率关系为根本，不仅方圆、周径之率为中算家所特别关注，而且勾股不失本率原理代替了西方的相似形理论成为几何测量的基础，甚至整数勾股弦的一般公式也是用比率的形式来表述的。
中国古代传统数学理论是一种“纲目结构”，纲举目张：目是组成理论之网的眼孔；纲是联结细目的总绳。《九章》以术为目，以率为纲，即是依算法划分理论单元，而用基本的数量关系把它们联结成一个整体。
（二）问题类型与数学模式
众所周知，要应用数学去处理实际问题，首先要把现实问题数学化。由现实问题到数学模型是一个抽象的思维过程，中国传统数学以寻求应用问题的一般解法为宗旨，因而从现实问题中抽象出一般的数学模式并设计出求解的机械化算法，这就构成了中国古算的基本框架。《九章算术》中的数学问题具有典型性，它们往往是现实生活中应用相当广泛的一类问题的代表，经过数学加工、提炼，成为一种特定的数学模型，问题的解法亦具有示范性，有举一反三之效。这与古希腊丢番图的《算术》“几乎没有得出求解的普遍法则”是大不相同的。
例如“方程”就是古代描述多元一次关系的数学模式，它标志着两千年前中算家在发展数学模式化方面所达到的高度。古代的“方程”即是用算筹布列成的数码方阵，每行上列诸数为物率，最下列之数为总实，其行数适与物数相等，它相当于现代多元线性方程组的增广矩阵。盈不足术是古代解一般数学应用问题的别开生面的算法，传入西方被称之为“双假设法”。这种方法的基本思想是，通过两次假设试验将实际应用问题转化为盈朒类数学模型，从而运用相应类型的机械化算法求解，即“现实问题→数学形式化→数学解答”的数学处理过程。
在中国古算中类似于盈不足术这样，用简单的趣味问题来描述一类数学模型是屡见不鲜的。《孙子算经》中的“物不知数”问，是古代著名的一次同余问题的数学模型，它来源于天文测算，古历法中的上元积年推算是它的现实原型。中国古代数学一开始便同天文历法结下不解之缘。在中国数学史上最有影响的“算经十书”，其中最早的《周髀》就是一部天文数学著作。中算史上许多具有世界意义的杰出成就是来自历法推算的。举世闻名的“大衍求一术”（一次同余式组解法）产生于历法上元积年推算；由于推算日月、五星行度的需要，中算家创立了“招差术”（高次内插法）；而由于选择历法数据的要求，历算家发展了分数近似法。
历法中的算法与太乙术数之类一样，被称为“内算”，秘不外传。正因为如此，流传现今的历代《律历志》中，一般只有历法数据而无算法。
不过，历法中的各种算法无疑都能在《九章》中找到它们的理论根源。
（三）中算的构造性与几何算术化的特点
《九章》中的题目可谓“有问必答”，它是中国古代传统数学表达方式中不可或缺的组成部分。一般说来，一个问题给出一组数值解，对于不定分析问题则给出多组解。从现代数学的观点来看，这种“有问必答”正反映了构造数学的主要特征。西方传统数学的公理化方法是非构造性的，这种非构造性观点，往往着眼于数学对象的存在性、唯一性和可能性等问题的讨论，而不大关心如何具体求出解答，或将能行的方法付诸有效的实现。构造性观点则要求用有限的方法将所需的数学对象构造出来。这两种观点的根本差异在于对数学对象存在性的不同理解。按照构造性的观点，为了证明存在一个具有性质
P
的事物
X
这样的断言，我们必须找出一个有限的方法来构造
X
，以及找出一个有限的方法来证明
X
具有性质
P
。
与此截然不同，按公理化方法所做的“纯粹的存在性证明”，即是一个事物
X
的“存在性”是通过采用指出假设“
X
不存在”就会导致矛盾的归谬法来证明的。
[1]
在纯粹的理论研究中，有许多问题一时难以给出构造性处理，而首先讨论其存在性、可能性等问题，自然是有意义的。但是问题最终的解决并付诸实用，还应当是构造性的。
《九章算术》中的答案都是由已知的数据按术文给出的算法，经有限步骤的运算而求得的。答案中虽然只列出数值解的数字，但从注释文字可以看出，中算家对于解的存在性与唯一性等问题是有所讨论的。事实上在“方程”求解的过程中，古代算家不可避免地要遇到有解无解，有唯一组解或多组解的不同情况，并且从演算中总结出存在性与唯一性的条件。在这方面刘徽的“九章注”有明确的记述。中算家虽然对于各类应用问题解的性质与构造具有相当深入的认识，但更专注于构造出此类问题求解的一般算法程序。中算“方程术”程序之科学合理，剩余定理构造之精妙完美，都堪称古代构造数学之典范。
《九章算术》采用的“有问必答”表达方式，也反映出中国传统数学几何算术化的特点。纯数学是以现实世界的数量关系与空间形式为其研究对象的。中国古代数学包含有丰富的几何内容，中算家在面积、体积和勾股理论方面取得了卓越的成就。然而，与古代希腊几何学迥然不同，中国古代的图形研究表现为数量的计算，它以长度、面积和体积等度量为主要对象，而一般不注重图形性质与位置关系的研究，甚至中国古代几何学不讨论角的性质与度量。几何对象的度量化，使中算“以算为主”的特点得以充分展现。虽然形数结合一般表现为几何方法与代数方法的相互渗透，但中国传统数学中几何算术化始终成为一种主要倾向。在中算家看来，一切几何对象都是可以计算的，几何的结论也可表现为几何对象间的数量关系，因而常常用其擅长的算法来解几何问题，这与古代希腊往往用几何作图的方法来处理代数问题正好相反。如果说古希腊几何学的主要方法是逻辑论证，那么中国古代几何学的基本手段就是数量计算。
（四）算法机械化与寓理于算的特点
中国古代数学称为“算术”，其本义是运用算筹的技术。算筹是我国古代特有的计算工具，它起初是人们随处可取的竹木细枝，后来发展为形制规整、做工精致的骨牙算筹。中国传统数学自始至终都与算器的应用密不可分，对算器有明显的依赖性，以致可以用“筹算”二字来代表中国古代的数学。中国古代从未有过西方那样的笔算；后来算经中的演草也只是筹算推演过程的简要书面记录。算筹是在计算机发明以前我国所独创并且是最有效的计算工具。
由于《九章》并非一部算术的启蒙读物，因此它对记数法没有专门的论述。关于筹算制度较早的记载见于《孙子算经》：“凡算之法，先识其位。一从十横，百立千僵，千十相望，万百相当。”
它强调算筹记数纵横相间与位值制原则。筹码记数有纵横二式；它从1至9的数码依次摆成下列形状：
纵式
横式
个、百、万……等位上的数码用纵式；十、千……等位上的数码用横式；筹码无“零”的符号，而用空位表示。例如“30745”记为“
”。筹算记数除了纵横相间与空位表“零”之外，在本质上与现今通行的阿拉伯数字记法没有什么不同。纵横相间有利于辨认数位，以空位表“零”对于算器记数并不是缺点。
中国古代的筹算决不限于单纯的数值计算，而是发展了一套内容十分丰富的“筹式”演算。中算家不仅利用筹码所在不同的“位”来表示不同的“值”，发明了十进位位值制记数法，而且还利用筹在算板上的各种相对位置关系来表示各种特定的数量关系，用以描述某种类型的实际应用问题。演算对象由“数”发展到“式”，即由数量进到数量关系的研究，后者具有更为一般的代数的性质。中国古代的筹式本身就具有代数符号的一般性的品格，是一种特殊的代数系统。
“术”是中国传统数学表达方式的核心部分。它记述解决所提出的一类问题的普遍方法，实际上就相当于现在计算机科学中的“算法”，在简单的情形下也相当于一个公式或一个定理。术文的内容通常包括如何布筹列式以及对筹式施行的演算程序。如果说算筹是电子计算机的“硬件”，那么中国古代的“算术”就是程序设计的“软件”。中国的筹算不用运算符号，无须保留运算的中间过程，只要求通过筹式的逐步变换而最终获得问题的解答。因此，中国古代数学著作中的“术”，都是用一套一套的“程序语言”所描写的程序化算法。各种不同的筹式都有其基本的变换法则和固定的演算程序，中算家善于运用演算的对称性、循环性等特点，将演算程序设计得十分简捷而巧妙。
“寓理于算”，可以说是中国传统数学理论在表现形式上的一个特点。中算家经常将其依据的算理蕴涵于演算的步骤之中，起到“不言而喻，不证自明”的作用。例如，《九章》中的“方程术”，由于将“方程”的每行视为一组比率（所谓“令每行为率”），于是施行于行列之间的乘除、并减运算便成为比率性质的自然应用，而消元求解的道理也就不言而喻了。
此外，算经中篇目的划分、题序的安排，一般也都或多或少地体现出其理论归属或内在的逻辑联系。
如果说西方数学公理化体系贯串一条明显的逻辑链，容易为人们所掌握，那么中国古算的机械化算法体系这种“隐蔽的”理论结构便难于为后世学者所认识。因此，研读《九章》的数学表达方式与理论结构极其重要。正所谓“《九章》翘楚宜详览，‘算术’精微总根源”！
《九章》与《原本》是大约同一时代的东、西方数学成就的总结。由于年代久远，这两部划时代数学巨著成书的确切年代均已无法断定。《九章》的成书年代曾是中国数学史研究的一大争鸣问题，众说纷纭，以早期钱宝琮主张的“东汉初年成书说”颇具影响。然而，近年来综合中国数学史的深入研究与考古发掘秦汉简帛的整理断定，魏人刘徽关于《九章算术》源流的叙述是有据而可信的。
《九章》并非一人一时之作，它集从西周迄秦汉我国古代数学之大成。作为我国古代流传至今的最早一部算经，《九章》是由先秦之遗残经西汉数学家张苍（约公元前250—前152）、耿寿昌（公元前1世纪中叶）等人几番删补而在西汉中期始成定本的。
中国古代数学由于其表达方式与早期书写条件的限制，数学的理论与原理未能诉诸文字，主要靠口授师传。自东汉以来，研习与注释《九章算术》者蜂起，他们或口授，或笔传，师弟相承，世代不绝，代有其人
，魏晋间人刘徽便是此中杰出的代表。他于魏陈留王景元四年（263）前后所撰的《九章算术注》成为不朽的传世之作。《九章》所采用的“问、答、术”的表达方式，显于“法”而隐于“理”，其中蕴涵的深邃的数学思想与精湛的数学理论只有通过刘徽的注释才得以阐明。而且，与《九章》的经文相比，刘徽的注释语句简略，用字深奥，内容博大精深。
关于刘徽的身世履历、生卒年代均无可详考。根据文献记载推断刘徽为魏晋间人，于263年前后注释《九章算术》
。由于他在生前没有显赫的社会地位，因此《晋书》中未能为之立传，据此今人推断刘徽是一位“布衣数学家”。《宋史·礼记》记载，北宋末算学祀典中刘徽曾被追封为“淄乡男”；另外，淄川临近渤海，而刘徽著有测望海岛的《海岛算经》一卷；由此推测他是现今山东淄川（今属山东淄博）一带人。也有文章考证认为祀典中对刘徽的封号是按其籍贯而来的，淄乡在今山东滨州邹平县境内，由此推断刘徽祖籍在今山东邹平，为汉淄乡侯的后代。
刘徽是中国古代杰出的数学家，在中算史上有着重要的地位，他最重要的贡献就是注释《九章算术》。刘徽所撰写的《九章算术注》（以下亦称《九章注》）十卷与《九章重差图》一卷，是中国数学史上划时代的著作。《九章算术注》十卷到唐代演变为《九章算术注》九卷与《海岛算经》一卷，《九章重差图》可惜在宋代已经失传。刘徽的《九章算术注》自问世以来便一直受到后世学人的推崇，被视为研习《九章》所必读。
刘徽的学术贡献可以概括为三大项：注《九章》，撰“重差”，创“割圆”。如果说第一项主要是对前贤学术传统的继承与阐发，那么后两项当归之为刘徽个人的发展与创新了。
刘徽是集前人之大成者，《九章注》中固然不乏其个人的独创，但其中的基本原理与论证方法大多还是前人已经有的。从理论的总体上看，刘徽注最杰出的成就便是它揭示出《九章算术》是一个“以率为纲”的算法理论体系。刘徽注“以率为纲”，用比率来解释《九章》中的各种算法，使其算理显豁而自然，收到了“纲举目张”之效。虽然，比率理论决非刘徽之首创，不过从留传后世的文献看，阐发得最为系统精辟的当推刘徽注了。
从传统几何学方面看，刘徽注的又一杰出成就在于它提炼出关于图形的基本数学原理，用以论证《九章》中的度量几何学公式。“出入相补”原理是对明显几何事实的概括，刘徽注用“出入相补”来论证《九章·方田》中各种简单直线形的面积公式。用“方”的分割来说明开方术的演算步骤，其根据仍在“出入相补”。虽然出入相补原理不能归之于刘徽所首创，但刘徽在应用这一原理方面有其发展与创新，其对整数勾股弦公式的几何论证就是精彩的一例。
他将多面体体积计算转化为其中所含立方个数的计算，从而实现了几何的算术化，其关键在于证明基本几何体之间的简单倍数关系，刘徽注运用极限观念完成了这一理论的严格证明。
截面原理素为中算家所熟悉与应用，成为中国古算求积理论的重要基础，刘徽与祖暅对这一原理都有广泛而精妙的应用。叠线成面，叠面成体乃是中算家传统的几何观念。对截面原理最成功的应用乃是关于球体积的计算。刘徽凭借对截面原理的深知与对图形性质的谙熟，发明了“牟合方盖”为球积公式的探求设计出正确的方案。可惜他功亏一篑未能计算出“方盖”之积，这一永载史册的创造最后由南北朝时代的祖暅最终完成。
刘徽的第二个学术贡献是撰“重差”。汉代的重差术其时似已失传，经过他的反复探究，终于“辄造重差，并为注解，以究古人之意，缀于勾股之下”。他的《海岛算经》原是作为《九章注》的延展部分撰写的，唐初才另本单行。《九章注·序》中以大半篇幅论述“重差”的意义及其由来，足见刘徽对它的重视。刘徽将源于窥天之重差施之于测地，类推衍化发展成《海岛》九术，把古代测量技术推向一个高峰。其重差造术之根据在于勾股比率，以两个差率代替勾、股之率是其中的关键。
“而且，重差理论中以量长代替角的测量的这一方法所隐含的以多次简易测量代替较难测量的原理，在现代的各种技术问题上可能还是有现实意义的。”
“割圆术”是《九章》中最长的一条注释，它用以论证“圆田术”，即圆的面积公式，并由此推算出较为精密的圆周率。刘徽术最可宝贵的创新在于“割圆拼方”与极限方法的运用。割圆拼方是刘徽割圆术的基本思想，他从中算家所熟悉的六觚，即圆内接正六边形出发，逐次等分圆周，将圆裁为边数依次倍增的觚形，而它又可以移补成半觚周为从、边心距为广的长方形。显然这种割圆拼方是一个近似的过程，圆面积在裁割中是有所失的，但当割圆为觚达到极限时，作为边心距与半径之差的“余径”便消失为零。于是边心距伸展为半径，半觚周伸展为半圆周，以半径为广、半周为从的长方形便与圆面积相等。这便是刘徽用极限方法证明圆积公式的过程大要。此外，刘徽依割圆所得筝形中所含小勾股弦与圆径、觚面之关系，列出依次计算边心距及余径，觚面与觚幂的循环递推程序，并由此逐步算得一百九十二觚之幂，从而推出圆周率
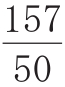，进而又“以率消息”得到更精确之圆率
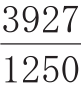。把“割圆术”列为刘徽三大学术贡献之一，足见数学史界对此项古代出色创作的推崇。
唐初以后，《九章》不仅作为国家颁行的主要数学教科书为莘莘学子传诵研习，而且远传朝鲜、日本及南亚诸国。明代中叶以后，随着中国传统数学的衰微，《九章》与刘徽注的内容已鲜为人知。自清代中叶戴震、李潢等以来对《九章》的整理与研究，实际上已经属于数学史的范畴了。
《九章算术》在我国历经两千多年辗转抄录、翻刻，其版本流传情况已不可详考。早在北宋元丰七年（1084）便有官家秘书省刻本，而流存迄今的最早善本是南宋嘉定六年（1213）鲍澣之在汀州的翻刻本（简称“南宋本”或“鲍刻本”）
。明代永乐六年（1408）编成的《永乐大典》，在“算”字条下分类抄录了《九章算术》的内容（简称“大典本”）
。南宋末年数学家杨辉的《详解九章算法》是《九章》的另一种版本，它“录经、注原文于前，而以其所撰题解、释注、比类、图说分附各条之后”（简称“杨辉本”）
。南宋本、大典本和杨辉本是《九章》流传迄今的三个明代以前的古本，可惜皆残缺不全。南宋本仅存方田、粟米、衰分、少广、商功五章；大典本现已大部分散佚；杨辉本只保存了商功、均输、盈不足、方程、勾股这后五章的内容
。
清代以来广为流传的《九章算术》的几个版本，主要是经著名学者戴震（1724—1777）辑录校勘的。清乾隆三十八年（1773）开四库全书馆，戴氏充《四库全书》纂修及分校官。次年，他从《永乐大典》中抄集《九章算术》九卷，并做了一番校勘工作，从而在辑录校注大典本的基础上，形成了四库全书本（简称“四库本”，成于1784年）
和武英殿聚珍版本（简称“殿本”，初刊于1774年）
《九章算术》。后者几经翻刻，并逐渐掺入了他人的校改，虽仍冠以“武英殿聚珍版”的名号，但前后各版多有不同
。1684年常熟汲古阁主人毛扆从南京黄虞稷处借得半部南宋本《九章算术》，影雕成汲古阁本《九章算经》
。1776年孔继涵得到汲古阁本，尔后成为戴震先后校订屈刻本和孔刻本的根据。屈刻本即乾隆四十一年（1776）常熟算家屈曾发刊刻的《九章算术》与《海岛算经》的合刊本，题称“豫簪堂藏版”。孔刻本即曲阜孔继涵刻《九章算术》，它是微波榭本《算经十书》之一。戴震校订屈、孔二氏的刻本大约是在1776年仲秋至1777年春他逝世之前。
此后依据微波榭本翻刻的《九章算术》有南昌梅启照的《算经十书》本和商务印书馆的《万有文库》本、《四部丛刊》本，等等。
在戴震之后，著名算家李潢（？—1812）以微波榭本为蓝本，撰成《九章算术细草图说》，在戴氏工作的基础上又校正了许多错误文字，并对难读的部分作图说、演细草。其中采用了李锐、戴敦元等人的校订稿的一部分，沈钦裴于李潢去世后遵嘱代为校算编辑，付梓前又做了个别的校正。李潢本后来亦多次被翻刻，是19世纪颇有影响的一个《九章》版本。
20世纪六十年代，钱宝琮以恢复唐代立于学宫的刘、李注本《九章算术》为宗旨，根据《天禄琳琅丛书》本和宜稼堂本《详解九章算法》，重新校点而收入中华书局出版的《算经十书》之中，成为20世纪中出现的第一个新的《九章算术》校勘本（简称“钱校本”）。1983年科学出版社出版了白尚恕的《〈九章算术〉注释》（简称“白注本”），它以钱校本为蓝本，参考各家之说，用通俗语言、近代数学术语对《九章》及刘、李注文详加注释。1991年仲夏，在本书初稿写成之后又见到了郭书春的汇校本《九章算术》，不久又得见白尚恕的《九章算术今译》（简称“今译本”）。这些著作作为《九章算术》的新版本，对于提高古算典籍整理的水平和推动《九章》及刘注研究向深层次发展无疑都产生了积极的作用。
[1] 按照构造性的观点，这种证明只是“表明 X 不可能不存在，但并未给出寻找 X 的方法”。甚至构造数学之极端主张不能接受逻辑的排中律。