




让我们回到圣路易斯博览会。你还记得吧,罗纳德·罗斯爵士也在参会的科学界大腕之列。1897年,他发现疟疾是通过按蚊的叮咬传播的。1904年,他已经是全球知名人士了,所以能邀请他到密苏里州做公开演讲是一件幸事——《圣路易斯邮报》的头条新闻标题是“蚊人来了”。
罗斯的演讲题目是《灭蚊卫生政策的逻辑基础》,我承认,这个话题听起来不太吸引人。但事实上,这场演讲是一种新的几何理论——“随机游走(random walk)理论”——投下的第一缕曙光。很快,该理论就会在物理学、金融学乃至诗体研究等领域引起巨大的反响。
罗斯是在1904年9月21日下午发表演讲的,与此同时,在博览会的另一处,伊利诺伊州州长理查德·耶茨正在检视获奖牲畜展。演讲开始后罗斯说道,假设你计划通过排干蚊子繁殖的水塘来消灭一个圆形区域内的蚊子,然而此举并不能彻底消灭这个区域内可能传播疟疾的所有蚊子,因为蚊子可以先在圆形区域之外繁殖,再飞进来。不过,一只蚊子的寿命很短,也没有执着的抱负,不会设定一条径直通往中心区域的飞行路线,所以它似乎不可能在短暂的一生内飞到圆形区域的深处。由此可见,只要这个圆形区域足够大,中心区域就有望摆脱疟疾的威胁。
那么,多大才算足够大呢?这取决于蚊子一生四处飞行的距离。罗斯说:
假设一只蚊子在给定的时间点出生,之后便开始随心所欲地四处飞行……过了一段时间,它死掉了。当它的尸体被发现时,与它的出生地相隔某个给定距离的概率是多少?
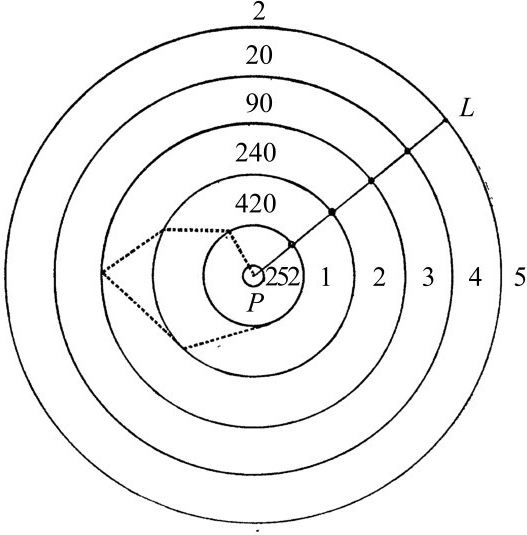
图4-1
图4-1是罗斯给我们提供的示意图。虚线表示四处闲逛型蚊子的飞行路径,直线表示目标导向型蚊子的飞行路径,相较之下,后一种蚊子在死亡之前的飞行距离更远。“这个问题背后的完整数学分析有些复杂,”罗斯说,“我无法在这幅图里将它全部呈现出来。”
在21世纪,你可以轻而易举地模拟一只沿罗斯路径运动的蚊子,这样你就能改进罗斯的示意图,看看在蚊子飞行10000次而不是5次的情况下会发生什么。
图4-2展示了一个有代表性的模拟结果:有时这只蚊子会在某个地方逗留一会儿,它的飞行路线纵横交错,几乎把附近的空间都填满了;而有时这只蚊子似乎又有了短暂的目标感,努力地朝着中心区域飞行一段距离。我必须告诉大家,这个过程的模拟动画看起来很有意思。
罗斯只会处理一种简单得多的情况:蚊子沿着一条固定的直线路径飞行,仅能选择往东北方向飞还是往西南方向飞。这种情况我们也能处理。假设一只蚊子的寿命是10天,它每天都会选择是往东北方向飞1千米还是往西南方向飞1千米,而且二者只能选其一。所以,这只蚊子可选的飞行路径总数为2×2×2×2×2×2×2×2×2×2=1024。假设这是一只无偏倚的蚊子,那么这些路径都是等可能性的。为了让这只蚊子在其出生地东北方10千米处死去,它必须连续10次选择往东北方向飞,而1024只蚊子中仅有一只能做到这一点。同样地,它在其出生地西南方10千米处死去的可能性也是这么小。所以,1024只蚊子中仅有两只能飞到10千米远的地方。那么,有多少只蚊子能飞到8千米远的地方呢?这要求蚊子每做出10次选择,其中有9次必须选择同一个方向,还有1次选择另一个方向,例如:

图4-2
东北,东北,东北,西南,东北,东北,东北,东北,东北,东北
仅有一次的“西南”可以位于10个位置中的任意一个,所以在1024条飞行路径中,有10条的终点在蚊子的出生地东北方8千米处,还有10条的终点在蚊子的出生地西南方8千米处,加起来是20条。如果你认真观察,就会发现罗斯在图4-1最外面的两个圆环上分别写了数字“20”和“2”。如果你愿意,你还可以写下蚊子死在其出生地东北方6千米处的45条路径,死在其出生地东北方2千米处的210条路径,或者飞回到它出生的恶臭池塘后死去的252条路径。在蚊子的所有死亡地点中,可能性最大的就是它的出生地。这是有道理的,因为这个关于蚊子的随机性问题其实相当于抛10次硬币,硬币正面朝上代表东北方,反面朝上则代表西南方。蚊子死在其出生地东北方8千米处,意味着硬币有9次正面朝上和1次反面朝上。蚊子回到出生地后死亡,意味着硬币正面朝上和反面朝上各有5次,而这确实是你抛10次硬币后最有可能得到的结果。如果你把不同的位置绘制成条形图,就会得到一条迷人的钟形曲线,它表明蚊子有靠近其出生地的倾向。
但我们还可以取得更多发现。稍微动动笔,你就能算出10天内蚊子的平均飞行距离为2.46千米。10天是雄蚊的典型寿命,而雌蚊的寿命更长一些,大约是50天,其间它们的平均飞行距离是5.61千米。玛土撒拉蚊(Methuselasquito)的寿命为200天,原则上它们的飞行距离可以达到200千米,但其死亡地与出生地的平均距离只有11.27千米。寿命增加了3倍,而飞行距离只增加了一倍。这条原则最早是在18世纪由亚伯拉罕·棣莫弗通过抛硬币(而不是在蚊子身上)发现的:如果抛n枚硬币,那么正面朝上的概率(真实值)与50%(平均值)之间的偏差通常在n的平方根附近。也就是说,如果一只蚊子的寿命是普通蚊子的100倍,那它的飞行距离很可能只是其短命表亲的10倍。一只蚊子的飞行距离有可能超出你的预期,但这种可能性不大。一只寿命为200天的蚊子死在距离其出生地至少40千米处的概率不到千分之三。