




正如几何学家现在看到的那样,对称性(symmetry)是几何学的基础。不仅如此,我们如何定义对称性还决定了几何学的走向。
在欧几里得几何中,对称性与刚体运动密不可分,包括平移、镜射、旋转及这三种运动方式的任意组合。对称性为我们讨论全等问题提供了一种更加现代化的方法。我们不说“如果两个三角形的所有边和所有角都相等,那么这两个三角形全等”,而说“如果一个三角形通过刚体运动能与另一个三角形重合,那么这两个三角形全等”。后一种说法是不是更自然?事实上,在阅读欧几里得的著作时,我们可以感觉到他本人竭力(但不能完全做到)避免以这种方式表达他的想法。
为什么要把刚体运动视为基本的对称性呢?一个不错(但也不太容易证明)的理由是,当我们让平面图形做刚体运动时,所有线段的长度完全相等,因此在希腊语中“symmetry”的意思是“等量”。其实,更恰当的希腊语词汇是“isometry”,它的意思是“等距”,正好对应于现代数学中的刚体运动。
图3-1中的两个三角形全等,所以我们倾向于像欧几里得那样宣称它们是相同的,尽管它们实际上并不相同。它们是间距约为3英寸的两个不同的三角形。
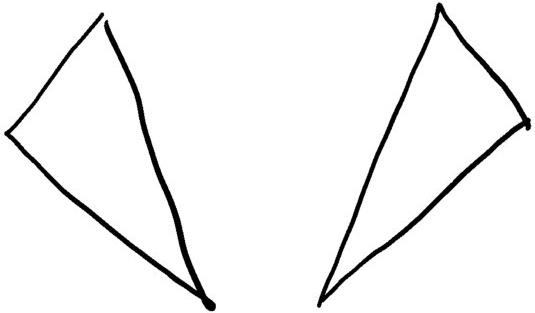
图3-1
这不禁让我们想起庞加莱的另一句常被引用的话:“数学是一门给不同的事物赋予相同的名称的艺术。”诸如此类的定义性崩塌现象在我们的日常思考和言谈中并不鲜见。想象一下,如果有人问你是否来自芝加哥,而你说“不是,我来自25年前的芝加哥”,这无疑是一个过于学究气的回答,因为当谈论城市时,我们会含蓄地引入时间平移对称性。遵照庞加莱的方式,我们用相同的名称指代过去的芝加哥和现在的芝加哥。
当然,对于“什么是对称性”的问题,我们的答案可能比欧几里得更严谨。例如,我们可能会禁止镜射和旋转,而只允许图形在不自旋的平面上滑动。这样一来,图3-1中的两个三角形就不再相同了,因为它们指向不同的方向。
如果我们允许旋转而不允许镜射呢?你可以认为这是困在平面上的三角形被允许进行的一类变换——我们可以滑动和旋转它们,但不能把它们拿起来和翻转,因为这需要使用我们现在被禁止探索的三维空间。在这些规则下,我们仍然不能用相同的名称指代这两个三角形。在左边的三角形中,从最短边到最长边是按逆时针方向排列的。无论我们如何滑动、旋转该图形,这个事实永远都不会改变;也就是说,它永远不可能与右边那个三角形重合,因为在后者中,从最短边到最长边是按顺时针方向排列的。镜射可以使顺时针和逆时针的方向互换,而旋转和平移则做不到。从最短边到最长边是按顺时针还是逆时针方向排列,这是三角形的一个特征,除镜射以外,它不受任何对称性的影响。我们称之为“不变量”。
每一类对称性都有其特定的不变量。刚体运动永远不会改变三角形或任何图形的面积,用物理学术语来说就是刚体运动遵循面积守恒定律。此外,它还遵循长度守恒定律,因为刚体运动不会改变线段的长度。

平面上的旋转很容易理解,不过,一旦进入三维空间挑战性就会大大增加。早在18世纪就有人(还是莱昂哈德·欧拉!)认识到,三维空间中的任何旋转都可以被视为绕某条固定的线(或轴)的旋转。虽然到目前为止一切顺利,但很多无法回答的问题也接踵而至。假设某个图形绕一条垂直线旋转20度,然后绕一条水平指向北方的直线旋转30度,那么最终的旋转一定是绕某个轴旋转某个度数,但到底是哪个轴和多少度呢?答案是:它大致相当于绕一个指向西北偏北方向的轴旋转36度。但这并不容易看出来!有人提出了一种更便利的思考方法,他将旋转看作一种数,即四元数。这个人就是华兹华斯的年轻朋友威廉·哈密顿。有一个著名的故事讲到,1843年10月16日,哈密顿和他的妻子在都柏林沿着皇家运河散步。嗯,我们还是让哈密顿自己来说吧:
虽然她时不时地跟我说话,但我的头脑中一直思绪万千,最终得出了一个结果。毫不夸张地说,我立刻感知到它的重要性。就像电路闭合、火花闪现一样……从布鲁厄姆桥上经过时,我情不自禁地用小刀在一块石头上刻下了这个基本公式……
哈密顿余生的大部分时间都在专心研究他的这一发现的相关推论,他甚至为此写了一首诗:“高等数学,魅力无穷/那些直线与数,是我们的主旋律。我们苦苦求索,希望看到她尚未出生的后代……”