





摘要 :本节内容将介绍第一宇宙速度、同步卫星和第二宇宙速度等概念,通过圆周运动规律求出地球的第一宇宙速度与同步卫星的轨道半径,在径向运动的特殊情况下得到第二宇宙速度的表达式,然后介绍并分析物体在万有引力下的能量守恒定律。最后,在极坐标下求解物体在万有引力下的运动轨迹,结果表明轨迹只能是椭圆、抛物线与双曲线这三种之一。
在这一课,我们回归一个最基础的问题——物体在万有引力作用下的运动问题。我们从大家比较关心的空间站来切入这个问题。空间站在天上一圈一圈地围绕地球旋转,它为什么不会掉下来?事实上,空间站一直都在往下掉,只不过因为它走得很快,它一边朝着地心掉下来,一边高速往前走,最终形成一个圆形或者椭圆形的运动。
在这里我们将详细求解物体(比如空间站和卫星)在引力场下的运动轨迹。引力场下物体的运动轨迹有很多用处,不过我们在这里关心的是,如果空间站碰到一块太空垃圾,或者被太阳风暴影响了一下,导致空间站的速度变化了一点,它会不会掉下来?为了解决这个问题,我们需要求出空间站在一般情况下的运动轨迹。
求解引力场中的物体运动轨迹,这不是中学物理能解决的。不过,在此之前,我们先用中学物理讨论一下第一宇宙速度和第二宇宙速度。我们知道,地球对地外小型物体的引力为:

其中 M 是地球质量, m 是物体质量, r 是物体到地心的距离。根据牛顿第二定律,有:
 (1)
(1)
α
是什么呢?
α
是加速度。我们考虑圆周运动的情况。前面我们说了,物体在做匀速圆周运动的时候,物体的速度大小虽然不变,但是它的方向不断在改变。它的加速度就来自速度方向的改变。假设物体圆周运动时的速度大小为
 ,半径为
r
,那么它的加速度大小为
,半径为
r
,那么它的加速度大小为
 。把加速度代入式(1)中,有:
。把加速度代入式(1)中,有:

等式两边的 m 和分母中的一个 r 都可以消掉,移一下项并开方就得到:
 (2)
(2)
这就是卫星在半径为
r
的圆周上环绕地球所需的速度,它是随着半径增大而减小的。我们所说的第一宇宙速度指的是卫星在贴近地球的轨道上环绕地球的速度,这可以通过将式(2)中的
r
换成地球半径
R
得到,换言之,第一宇宙速度为
 。
。
我们可以利用大家熟知的重力加速度
g
替换掉第一宇宙速度公式中的
GM
。质量为
m
的物体在地球表面受到的引力为
 ,而这个引力就等于我们平时所说的物体重力
mg
,所以
,而这个引力就等于我们平时所说的物体重力
mg
,所以
 ,或者写为
,或者写为
 。利用这个结果替换掉第一宇宙速度公式中的
GM
就得到
。利用这个结果替换掉第一宇宙速度公式中的
GM
就得到
 。地球半径大约是6400千米,所以:
。地球半径大约是6400千米,所以:

这就是第一宇宙速度的值。对于离地球比较近的轨道,卫星必须达到这个速度才能保证不掉下来。因为环绕速度随着半径增大而减小,所以半径大的轨道上面的卫星,速度是小于第一宇宙速度的。
空间站在我们的头顶都是很快速地飞过的,那有没有一种卫星,在我们头顶是悬停不动的呢?这似乎不太可能,如果它悬停不动,那它不就在引力的作用下直接掉下来了吗?但是我们不要忘了,地球是不停地在自转的。如果这个卫星绕着地球转的角速度刚好等于地球自转的角速度,那么相对于地上的人来说,这个卫星不就是悬停不动的吗?这种卫星就是我们所说的同步卫星。下面我们来计算一下同步卫星的轨道半径,看看这个半径需要多大。
对于圆轨道的卫星速度,我们有:

其中根号里边的分子已经使用前面提到的
 进行了替换。又因为角速度和速度的关系是
进行了替换。又因为角速度和速度的关系是
 ,把它代进速度公式就可以得到:
,把它代进速度公式就可以得到:
 (3)
(3)
根据我们前面的讨论,同步卫星的角速度和地球自转角速度一样。换言之,同步卫星绕地球转的方向和地球自转方向一致,并且角速度的大小要满足大约一天转一圈。一圈是
 弧度,所以在单位rad/s下角速度
ω
的数值为
弧度,所以在单位rad/s下角速度
ω
的数值为
 。目前我们的情况是,已知角速度,求卫星的轨道半径,所以需要从式(3)中解出半径
r
:
。目前我们的情况是,已知角速度,求卫星的轨道半径,所以需要从式(3)中解出半径
r
:

代入数值可以得到,同步卫星的轨道半径大约是42000千米。这是非常远的距离,差不多是地球半径的6.6倍。
接下来我们求地球表面的第二宇宙速度。第二宇宙速度指的是,物体从地球表面飞出并且能逃离地球的引力束缚飞到无穷远(忽略别的星球的引力影响)所需要的最小初速度。考虑物体沿地球径向飞出,如果物体能够飞到无穷远并且飞到无穷远之后速度刚好降为0,那么它的初速度就是第二宇宙速度。
怎么求第二宇宙速度
 呢?这就需要我们之前讲过的动能定理:力对物体做的功,等于物体动能的改变量。地球对物体的引力与飞出的物体运动方向相反,因此引力对物体做负功。假设物体质量为
m
,物体从地面飞到无穷远时引力做的功为:
呢?这就需要我们之前讲过的动能定理:力对物体做的功,等于物体动能的改变量。地球对物体的引力与飞出的物体运动方向相反,因此引力对物体做负功。假设物体质量为
m
,物体从地面飞到无穷远时引力做的功为:

物体的初始动能为
 。当它飞到无穷远处时速度刚好降为0,所以末动能为0。根据动能定理,有:
。当它飞到无穷远处时速度刚好降为0,所以末动能为0。根据动能定理,有:
 (4)
(4)
所以

第二宇宙速度正好是第一宇宙速度的
 倍,于是我们立刻可以计算得到地球的第二宇宙速度大约为11.2 km/s。
倍,于是我们立刻可以计算得到地球的第二宇宙速度大约为11.2 km/s。
我们这里推导第二宇宙速度用的是沿径向飞出的特例,但是,如果物体不是沿径向飞出呢?比如它沿着地面水平飞出,它能不能飞到无穷远?抑或它会在引力的作用下拐个大弯最后又飞回地面?答案是,它能飞出地球去到无穷远处。要全面回答这个问题,我们需要求解出物体的轨迹方程,这将会是这次课程和下一次课程的主要任务。
在求出轨迹方程之前,我们也可以利用引力场下的机械能守恒来理解为什么沿其他方向以第二宇宙速度飞出同样能飞到无穷远。所谓机械能,就是物体的动能和引力势能之和。动能我们之前讲过,那引力势能呢?这就需要回到引力公式来理解。质量为 m 的质点在地球外面受到的引力为:

矢量
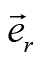 是径向单位矢量,它可以写为
是径向单位矢量,它可以写为
 ,所以引力可以写为:
,所以引力可以写为:

当物体在引力场下运动了
 ,引力做的功为:
,引力做的功为:

为了处理这个式子,我们需要一些处理矢量的技巧:

所以,万有引力做的功可以改写为:
 (5)
(5)
另一方面,外力做的功等于物体动能的改变量:
 (6)
(6)
综合式(5)和式(6)立即可以得到:

其中
 是物体的动能,
是物体的动能,
 被定义为物体距离地球为
r
时的势能。这个结果的物理意义是,在万有引力的作用下,机械能,也就是动能和势能之和,是保持不变的。
被定义为物体距离地球为
r
时的势能。这个结果的物理意义是,在万有引力的作用下,机械能,也就是动能和势能之和,是保持不变的。
现在让我们回头看式(4),它表示以第二宇宙速度从地面起飞的物体的机械能是0:

当物体飞到无穷远时,引力势能公式中的
 ,所以引力势能为0。又因为机械能为0,所以物体飞到无穷远时的动能刚好降为0。这里的讨论不依赖于物体的运动路径,只和它的初态和末态有关。因此,从机械能守恒的角度来看,物体以第二宇宙速度沿不同方向飞出,都有可能飞到无穷远。不过,这里的讨论只是论证了从其他方向飞到无穷远不违背机械能守恒,不代表它一定能飞到无穷远。
,所以引力势能为0。又因为机械能为0,所以物体飞到无穷远时的动能刚好降为0。这里的讨论不依赖于物体的运动路径,只和它的初态和末态有关。因此,从机械能守恒的角度来看,物体以第二宇宙速度沿不同方向飞出,都有可能飞到无穷远。不过,这里的讨论只是论证了从其他方向飞到无穷远不违背机械能守恒,不代表它一定能飞到无穷远。
在这里,我们终于要开始着手求解物体在引力场中的运动轨迹了。因为引力只沿径向方向,所以采用极坐标能一定程度地简化方程。极坐标的基矢会随着位置的不同而不同,随着质点的运动,质点位置的极坐标基矢会不断变化,从而其对时间的导数不为0。为了后面的讨论,我们先来求极坐标基矢对时间的导数。考虑在
t
到
 这段时间下,质点从
这段时间下,质点从
 运动到了
运动到了
 ,基矢
,基矢
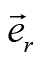 和
和
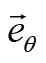 的变化如下图所示。
的变化如下图所示。

极坐标基矢的变化情况
注意,上图的角度变化d
θ
已经经过了夸大处理,实际上它是一个微量。为了求基矢在
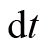 时间内的改变量,我们需要将不同时刻的对应基矢移到同一点上。从图中可以看出,
时间内的改变量,我们需要将不同时刻的对应基矢移到同一点上。从图中可以看出,
 和
和
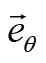 同向,
同向,
 和
和
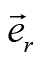 反向。
反向。
 和
和
 的大小都可以利用弧长公式估算出来,对应的角度是d
θ
,对应的“半径”分别是
的大小都可以利用弧长公式估算出来,对应的角度是d
θ
,对应的“半径”分别是
 和
和
 。于是
。于是
 。再根据刚刚提到的
。再根据刚刚提到的
 和
和
 的方向,我们有:
的方向,我们有:

接下来我们使用一个撇号表示对时间的一阶导数,两个撇号表示对时间的二阶导数,比如
 和
和
 。那么:
。那么:

质点的位置矢量为
 ,速度等于位置矢量对时间的导数,所以:
,速度等于位置矢量对时间的导数,所以:

加速度等于速度对时间的导数,所以:

对于匀速圆周运动,
 ,所以
,所以
 ,速度大小
,速度大小
 ,这也说明了
,这也说明了
 。利用这些结果,匀速圆周运动的加速度为:
。利用这些结果,匀速圆周运动的加速度为:

加速度大小为
 ,这是前面计算第一宇宙速度时使用的结论。
,这是前面计算第一宇宙速度时使用的结论。
回到一般轨迹的运动上,设质点的质量为 m ,根据牛顿第二定律,我们得到:

代入加速度的公式,消去两边的共同因子 m ,然后分别考虑角向部分和径向部分,就能得到一组等式:
 (7)
(7)
 (8)
(8)
我们先来看看式(8),它的左边可以改写为
 ,也就是说
,也就是说
 ,换言之,在粒子运动的过程中,
,换言之,在粒子运动的过程中,
 是个常数,我们记这个常数为
α
。我们知道,
是个常数,我们记这个常数为
α
。我们知道,
 表示质点和原点的连线在单位时间内转过的角度,所以
表示质点和原点的连线在单位时间内转过的角度,所以
 表示质点和原点的连线在单位时间内扫过的面积,它是个常数。这正是开普勒第二定律。
表示质点和原点的连线在单位时间内扫过的面积,它是个常数。这正是开普勒第二定律。
我们再看式(7),它里边含有
 ,不过我们可以用
,不过我们可以用
 将其替换掉,这样就得到:
将其替换掉,这样就得到:
 (9)
(9)
由于我们的目标是求出质点的运动轨迹,在极坐标下轨迹一般通过
 表示出来,所以我们需要将
r
对时间的导数转化成对
θ
的导数,这通过基础的导数运算可以做到。比如说:
表示出来,所以我们需要将
r
对时间的导数转化成对
θ
的导数,这通过基础的导数运算可以做到。比如说:

上式已经用
 进行了替换。这是一个普遍结果,用于将时间导数换成角度导数。利用这个结果,我们先来处理
进行了替换。这是一个普遍结果,用于将时间导数换成角度导数。利用这个结果,我们先来处理
 :
:

在这个结果的基础上,我们处理
 :
:
 (10)
(10)
这个结果以及式(9)都含有很多
 的倒数,因此,直觉上感觉进行变量代换
的倒数,因此,直觉上感觉进行变量代换
 能简化方程。为此,我们考察一下
能简化方程。为此,我们考察一下
 对
θ
的一阶导数及二阶导数:
对
θ
的一阶导数及二阶导数:

神奇的事情发生了!对比式(10)最后的方括号里边的量,和上式
 一模一样!因此:
一模一样!因此:

将这个结果代入式(9)并化简,可以得到:

这个方程的解很简单,是
 ,其中
,其中
 。我们可以选取角度坐标起点使得
。我们可以选取角度坐标起点使得
 ,因此方程的解可以写为
,因此方程的解可以写为
 。对于常数
A
,我们需要利用质点的初始条件才能确定下来,不过我们总可以选取角坐标使得
。对于常数
A
,我们需要利用质点的初始条件才能确定下来,不过我们总可以选取角坐标使得
 。考虑到
。考虑到
 ,所以质点的轨迹为:
,所以质点的轨迹为:

这个极坐标方程对应的曲线分别是椭圆(当
 )、抛物线(当
)、抛物线(当
 )和双曲线(当
)和双曲线(当
 )。当轨迹是椭圆时,我们可以找到轨迹上的近地点和远地点。所谓近地点,就是轨迹上离地球最近的点,远地点则是离地球最远的点。
θ
的取值范围是0到
)。当轨迹是椭圆时,我们可以找到轨迹上的近地点和远地点。所谓近地点,就是轨迹上离地球最近的点,远地点则是离地球最远的点。
θ
的取值范围是0到
 ,因此
,因此
 的取值范围是-1到1,
θ
=0时对应近地点,距离为
的取值范围是-1到1,
θ
=0时对应近地点,距离为
 ;
;
 时对应远地点,距离为
时对应远地点,距离为
 。
。
这次课程的前半部分内容比较简单,只需要用到高中的物理知识;后半部分内容,特别是其中的轨迹求解,需要用到不少微积分的知识。读者们可以通过这里的计算来复习并掌握相关知识。卫星的运动轨迹在历史上是一个经典问题。在牛顿之前,开普勒已经通过实验观测得到了行星围绕太阳运动的三大定律。后来,牛顿根据开普勒定律反推得到万有引力随距离平方成反比的形式。总的来说,是牛顿最先解决了卫星和行星的运动轨迹问题。轨迹方程的导出有利于我们分析各种各样和卫星、行星相关的问题。在下一节,我们将在此基础上详细分析以第二宇宙速度朝各个方向发射能否逃离地球的引力束缚,和空间站受到微小扰动时会怎么改变运动状态这两个问题。