





摘要 :本节将从基础的牛顿定律出发,介绍万有引力定律和电荷的库仑定律,再到卫星、飞船的速度和角速度计算,一幅壮丽的物理图景即将展开。
自然界中存在四种基本的相互作用力——电磁力、强相互作用力、弱相互作用力以及万有引力。它们构成了我们丰富多彩的世界,解开这些力的规律,就能解释这个世界的绝大多数现象。在经典力学中,我们用一个三维矢量来描写相互作用力,并且力满足牛顿三大运动定律。牛顿第一定律是指在没有外力作用下孤立质点保持静止或做匀速直线运动;牛顿第二定律指力等于质点质量乘以质点的加速度;牛顿第三定律则是指相互作用的两个质点之间的作用力和反作用力总是大小相等、方向相反,并且作用在同一条直线上。不过牛顿运动定律只给出了关于力的普遍性质,并未确定力的具体表达式,于是本节课将介绍两种力的具体形式,即万有引力与库仑力,并结合牛顿运动定律来具体做一些计算。
物理大厦的基础是牛顿力学,所以我们需要从这里开始讲起。要了解牛顿力学,必然离不开“力”这个基本概念。牛顿三大定律里,后两个定律直接说到力。牛顿第一定律虽然没有直接对力做出限定,却描述了不受力作用的物体的运动状态。总之,牛顿三大定律都与力有关,可见此概念的重要性。
力的作用表现为改变物体的运动状态。如果没有力,物体将会静止或者一直保持原来的速度运动下去。这就是牛顿第一运动定律。如果力作用在质点上,质点的运动状态就会改变。牛顿力学里通过加速度来描述运动状态的改变。加速度被定义为单位时间内速度的改变量,也就是速度对时间的导数:

牛顿第二运动定律说的是力和加速度的关系:

其中
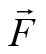 表示作用在质点上的力,
m
是这个质点的质量。我们平时说的100斤,指的就是质量。质量是用来衡量物质多少的量,同时也表征了物体受到力的作用后运动状态改变的难易程度。
表示作用在质点上的力,
m
是这个质点的质量。我们平时说的100斤,指的就是质量。质量是用来衡量物质多少的量,同时也表征了物体受到力的作用后运动状态改变的难易程度。
牛顿第二定律是比较容易理解的:当静止的物体受到一个恒力的作用,它必然会不断加速;当运动的物体受到反向的力的作用,就会不断减速。这些结论都符合人们的观念。
有时候人们很难直接测量力的大小,但是只要知道了物体的运动状态,算出它的加速度,再乘以质量就可以得到力了。于是,牛顿第二定律不仅表明力使物体的运动状态发生改变,还说明我们可以通过加速度去测量力。
自然界中存在四种基本相互作用,它们分别是引力相互作用、电磁相互作用、强相互作用和弱相互作用。其中强相互作用和弱相互作用主要发生在原子核及以下尺度。而引力相互作用,就是所谓的万有引力。比如两个相距 r 的质点,质量分别为 m 1 和 m 2 ,那么它们之间存在着吸引力,大小为:

其中
 是万有引力常数。不管物体距离多远,也不管是什么类型的物体,比如搜狐大厦这栋楼,或者远在西雅图的某栋楼,都会对地球上的人有吸引力,只不过这个吸引力很小,人们一般难以察觉。但是对于宇宙中的星体等大质量的物体,引力的相互作用就变得很大了。太阳系乃至银河系的各种运动几乎都是引力在主宰。
是万有引力常数。不管物体距离多远,也不管是什么类型的物体,比如搜狐大厦这栋楼,或者远在西雅图的某栋楼,都会对地球上的人有吸引力,只不过这个吸引力很小,人们一般难以察觉。但是对于宇宙中的星体等大质量的物体,引力的相互作用就变得很大了。太阳系乃至银河系的各种运动几乎都是引力在主宰。
前面介绍的引力公式是对两个质点进行描述的,但是像星体这种密度只随半径变化的球体,其外部引力可以等效为同等质量的质点的引力,且等效质点处于球心位置。这个结论将会在以后的小节中给予证明,目前先默认这一点。
在地球表面附近,所有物体都受到重力作用,这个重力主要来源于地球对物体的万有引力。重力垂直向下,大小是
 ,其中
,其中
 是重力加速度。我们要区分重量和质量这两个概念。重量指的是物体受到的重力大小,质量指的是物体含有的物质多少、惯性的大小。一个质量为
是重力加速度。我们要区分重量和质量这两个概念。重量指的是物体受到的重力大小,质量指的是物体含有的物质多少、惯性的大小。一个质量为
 的人,他的重量大约是980N。
的人,他的重量大约是980N。
在地球附近,有如下关系:

其中
M
是地球质量,
R
是地球半径。消掉
m
,可得到
 。在很多计算中,可以利用这个关系替换掉其中的
GM
。
。在很多计算中,可以利用这个关系替换掉其中的
GM
。
接下来我们来简单讨论电磁相互作用。虽然电磁现象可以通过麦克斯韦理论描述,但是电磁力可以被区分成很多种力,这里介绍的是电荷间的作用力,更严格地说是静电荷之间的力。静电力的公式与万有引力公式非常相似:

其中
q
1
和
q
2
是两个点电荷的电荷量,
r
是这两者之间的距离,
 是静电常数。静电力和引力一样,都与距离的平方成反比,且力的方向是沿着两个点电荷之间的连线。而电磁力与引力不一样的地方在于电荷有正有负,从而使得点电荷之间可能是吸引力,也可能是排斥力,表现为同种电荷互相排斥,异种电荷互相吸引。
是静电常数。静电力和引力一样,都与距离的平方成反比,且力的方向是沿着两个点电荷之间的连线。而电磁力与引力不一样的地方在于电荷有正有负,从而使得点电荷之间可能是吸引力,也可能是排斥力,表现为同种电荷互相排斥,异种电荷互相吸引。
既然静电力也是与距离的平方成反比,那么为什么星体之间的运动由引力主宰?这是因为异种电荷互相吸引,所以行星尺度上各种物体整体看来都是接近电中性的,从而几乎不存在静电力。而引力没有这种互相抵消的效应,越多质量堆叠在一起,引力就越强。
如何计算卫星或者空间站的速度?卫星和空间站在天上只受到引力作用,没有其他力帮忙平衡住引力,为什么它们不掉下来?这是因为它们在做圆周运动。严格说来,实际上它们做的一般是椭圆运动,不过为了计算方便,此处暂且将之近似为匀速圆周运动。
既然卫星受到地球的引力作用,方向指向地心,那么卫星应该有一个指向地心的加速度。卫星做的是匀速圆周运动,它的速度大小不变,何来的加速度呢?这是因为速度是个矢量,虽然它的大小不变,但其方向一直在发生变化。以地心为原点,在圆周运动所在的平面上建立极坐标,由于速度方向始终垂直于半径,速度大小不变的时候,由简单的几何关系可知,卫星运行了一个微小角度
 后速度的变化为:
后速度的变化为:

由加速度的定义还可得加速度大小为:
 (1)
(1)
其中
 是角速度,一般用
ω
表示。同样,因为弧长等于角度
θ
乘以半径
r
,可以得到速度和角速度的关系为:
是角速度,一般用
ω
表示。同样,因为弧长等于角度
θ
乘以半径
r
,可以得到速度和角速度的关系为:
 (2)
(2)
其中
r
为圆周运动的半径。联立式(1)与式(2)可得加速度大小与速度的关系式
 。由于速度保持不变,所以加速度垂直于速度方向,而前面也说过了速度方向始终垂直于半径,那么加速度方向沿着半径指向地心。引力也是指向地心的,根据牛顿第二定律,有:
。由于速度保持不变,所以加速度垂直于速度方向,而前面也说过了速度方向始终垂直于半径,那么加速度方向沿着半径指向地心。引力也是指向地心的,根据牛顿第二定律,有:

由此得到速度大小为:

联立式(2)可以计算出卫星绕地球运行的角速度:

进一步利用前面介绍的
 ,可得角速度与重力加速度
g
的关系:
,可得角速度与重力加速度
g
的关系:

地球半径大约是6400千米。假设某卫星或飞船的高度为590千米,代入数据可以得到相应的角速度为
 ,也就是一天大约绕地球15圈。中国空间站高度大约是400千米,同样可以计算得到空间站一天绕地球大约16圈。
,也就是一天大约绕地球15圈。中国空间站高度大约是400千米,同样可以计算得到空间站一天绕地球大约16圈。
本节课介绍了两种相互作用力——万有引力以及库仑力,实际上库仑力是四大基本力中电磁力的一部分,但电磁力包含更多更复杂的内容。有了力的具体表达式,结合牛顿运动定律就可以求出物体的运动了,我们不仅能通过计算解释已有现象,还能定量地预测未来,这为人类的太空探索带来了巨大的力量。