





摘要 :这一节我们推导空气中的声音波动方程。在一些合理的近似下,我们会发现声波方程和前面介绍的琴弦振动方程是一样的,因此我们能利用前面的结论得到声速的公式,并证明室温下的空气声速为340 m/s。和琴弦的问题不同的是,推导空气声波方程时我们需要使用一些热力学知识。
我们平时说话时对方能立即听到,这给人一种错觉,仿佛声音的传播是瞬时的。实际上声音的传播需要时间,只不过因为声速很大,在说话的距离上我们察觉不到声音的延迟而已。但是相对于物理世界中的很多速度等级,声速是比较小的。平时打雷的时候,我们先看到闪电过几秒后才听到声音,就表明声速比光速慢得多。
在深入了解声音波动方程之前,我们先来提两个问题:空气变稀薄会影响声速吗?在冬天的时候,哈尔滨的声速和海南的声速一样吗?接下来我们将利用基本的微积分及物理知识,介绍如何推导声音的波动方程,并从中得到声速的表达式,回答这里提到的两个问题。根据我们得到的声速公式,我们可以计算出和声速测量值非常接近的理论值。
回忆前面处理琴弦振动时的做法,用
 表示琴弦对静平衡位置的偏离,然后对琴弦上的质量微元进行受力分析,根据牛顿第二定律得到琴弦的波动方程。在这里我们的处理方法也一样,毕竟我们不能将牛顿第二定律应用在整个空气上面,这样做是得不到声音的波动方程的。
表示琴弦对静平衡位置的偏离,然后对琴弦上的质量微元进行受力分析,根据牛顿第二定律得到琴弦的波动方程。在这里我们的处理方法也一样,毕竟我们不能将牛顿第二定律应用在整个空气上面,这样做是得不到声音的波动方程的。
当没有声音时,空气会维持在平衡状态上,其中的各个物理量,如密度、温度等,都不随位置和时间而改变。在后续推导中,空气静平衡状态下的量将用下标0标注。和琴弦振动不一样的是,声音是一种密度波,它通过空气的振动来传播,空气微元的振动方向和传播方向平行,所以声波是纵波。当声音出现在空气中时,空气微元会偏离原来的位置。为简单起见,我们在这里仅考虑一维的情形。用
 表示初始位置在
x
的空气微元在
t
时刻的偏移。在
x
位置处取一个截面积为
A
、厚度为
表示初始位置在
x
的空气微元在
t
时刻的偏移。在
x
位置处取一个截面积为
A
、厚度为
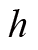 的空气窄片。窄片在声音到来时的加速度可以由
的空气窄片。窄片在声音到来时的加速度可以由
 对时间的二阶偏导数得到。窄片偏离平衡位置后会受到压力使它恢复平衡位置,这个压力由截面的压强
P
提供,等于:
对时间的二阶偏导数得到。窄片偏离平衡位置后会受到压力使它恢复平衡位置,这个压力由截面的压强
P
提供,等于:

记空气密度为
 ,根据牛顿第二定律,我们有:
,根据牛顿第二定律,我们有:

如前面说的那样,下标0表示静平衡时的值。消去
A
和一个
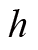 之后让
之后让
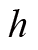 趋于0,我们得到:
趋于0,我们得到:
 (1)
(1)
声音传播过来时,空气会被压缩或者拉伸,于是空气的局部密度改变了,从而导致压强的改变。我们可以借助密度的变化量
 得到压强:
得到压强:

看到这里大家可能会疑问,这里压强
P
对密度的偏导数的准确定义是什么?根据理想气体状态方程,描述理想气体的状态需要两个物理量,而这两个量的选取具有任意性,因此必须明确这里
P
对
 的偏导数是在保持哪个物理量不变的情况下的偏导数。对于这个问题,我们留到后面再进行详细的解答。
的偏导数是在保持哪个物理量不变的情况下的偏导数。对于这个问题,我们留到后面再进行详细的解答。
定义

于是
 (2)
(2)
接下来我们需要在
 和
和
 之间建立关系。再次取平衡位置
x
处,截面积为
A
、厚度为
之间建立关系。再次取平衡位置
x
处,截面积为
A
、厚度为
 的空气窄片,它的密度是
的空气窄片,它的密度是
 。当声音传过来时,窄片的密度变成了
。当声音传过来时,窄片的密度变成了
 ,并且窄片两端都分别做出了偏移,偏移量由函数
f
描述。根据质量守恒,有:
,并且窄片两端都分别做出了偏移,偏移量由函数
f
描述。根据质量守恒,有:

等式两边消去
A
和一个
 ,并让
,并让
 趋于0。由于
趋于0。由于
 趋向于0,我们得到:
趋向于0,我们得到:

将上式的乘积展开,有:

上式等号左边的项和等号右边第一项互相抵消。对于空间中的声波,我们一般会假设它的振幅很小,而且声波的频率相对较小,以至于
 远小于1。在这些假设不成立的情况下,声音的传播过程会出现复杂的非线性现象。在此假设基础上,上式最后一项相比于其他项要小得多,因此可以忽略。于是:
远小于1。在这些假设不成立的情况下,声音的传播过程会出现复杂的非线性现象。在此假设基础上,上式最后一项相比于其他项要小得多,因此可以忽略。于是:

将式(2)和上述结果依次代入式(1),可以得到:

消去
 立即得到:
立即得到:

这就是声音在空气中的波动方程。根据我们在处理琴弦波动方程时得到的结论, α 等于声速的平方。
得到声音的波动方程之后,为了求出声速,我们必须先得到
α
的表达式,为此,我们需要弄明白
 的具体意义。
的具体意义。
在牛顿当年推导声音的表达式之时,他也面临了同样的问题。牛顿认为声音在传播过程中空气的温度是不变的,这和我们的直观感受一致,因为我们确实没有在听到声音的同时感受到温度在变化。考虑到理想气体状态方程
 ,
N
是空气分子数,
k
为玻尔兹曼常数。设空气分子平均质量为
,
N
是空气分子数,
k
为玻尔兹曼常数。设空气分子平均质量为
 ,我们有:
,我们有:

所以,当温度不变时,有:

我们已经在上式的分子分母上分别乘以了阿伏伽德罗常数
 。根据热力学知识,
。根据热力学知识,
 为理想气体常数,约等于
为理想气体常数,约等于
 ,
,
 等于空气的摩尔质量
等于空气的摩尔质量
 。所以,我们有:
。所以,我们有:

如果牛顿的假设是正确的话,那么声速应该等于
 。以
。以
 为单位时,摩尔质量的数值刚好约等于分子的核子数。对于空气分子,平均核子数为29,所以它的摩尔质量约等于
为单位时,摩尔质量的数值刚好约等于分子的核子数。对于空气分子,平均核子数为29,所以它的摩尔质量约等于
 。温度
T
代表绝对温度,以开尔文为单位,
T
比摄氏温标的值高273.15。于是,在室温20摄氏度时
T
等于293.15开尔文。代入室温下的数值,我们发现这个“声速”为290 m/s,和实际值340 m/s相差很大。
。温度
T
代表绝对温度,以开尔文为单位,
T
比摄氏温标的值高273.15。于是,在室温20摄氏度时
T
等于293.15开尔文。代入室温下的数值,我们发现这个“声速”为290 m/s,和实际值340 m/s相差很大。
实际上,由于声音会造成空气的压缩和拉伸,空气温度不可能是不变的,因此牛顿的假设存在相当大的误差。另外,相对于声波导致的快速压缩和膨胀,空气的热传导过程非常缓慢。在空气的一个振动周期里,热的传导几乎可以忽略,因此应该把声音传播导致的空气压缩和膨胀看成是绝热过程而非等温过程。我们称之为绝热近似。
接下来我们在绝热近似下计算声速。因为这里考虑的声音振幅很小,相对于空气的振动来说,空气微元内恢复平衡的速度非常快,因此可以假设在空间的每一处空气都满足理想气体状态方程。这个近似我们称为准静态近似。对于特别稀薄的空气准静态近似是不成立的,因此这里对声速的推导不适用于特别稀薄的空气。
根据我们在介绍理想气体的热力学性质时得到的结果,理想气体的绝热准静态过程满足:

其中
 是绝热常数,对于单原子分子
是绝热常数,对于单原子分子
 ,对于温度不是特别高的双原子分子
,对于温度不是特别高的双原子分子
 。空气中大部分是氮气和氧气,都是双原子分子,因此这里取1.4。因为密度和体积成反比,所以存在常数
b
使得绝热过程下有:
。空气中大部分是氮气和氧气,都是双原子分子,因此这里取1.4。因为密度和体积成反比,所以存在常数
b
使得绝热过程下有:

于是:

其中下标 s 表示绝热过程。所以声速满足:

直观来看,声速似乎和压强以及密度有关,但是这种相关性是表面的,因为压强改变时体积也有可能变化,从而导致密度变化,这样的情况下压强与密度同时改变有可能正好使得声速不变。为了看出这一点,我们将
 代入,有:
代入,有:

所以空气中的声速为:

可见空气中的声速值只和温度有关,和压强与密度并没有关系,除非压强改变时导致了温度的变化。根据这个结果,在室温20摄氏度时的声速约为:

这个值与大家熟知的340m/s非常接近。可见,绝热近似是一个合理的近似。
观察声速公式,我们可以知道声速只和温度有关,和空气的稀薄程度无关。如果忽略温度随着海拔改变的变化,不同高度的声音速度是一样的,不会因为空气在山上变稀薄了声速就变小或者变大了。这就回答了前面一开始提的第一个问题。当然,这个论断只适用于足够稠密的空气。当空气变得异常稀薄时,前面所做的准静态假设会失效,因此这里的推导结果不足为信,声速公式也需要进行修正。
因为声速和温度有关,所以我们也能回答第二个问题了。忽略声速公式中的常数,并将绝对温度换成摄氏温度,我们有

上式中的 t 表示摄氏温度。假设冬天的某一时刻,寒冷的哈尔滨气温为零下30摄氏度,而温暖的海南气温为零上20摄氏度,由于

我们可以知道,哈尔滨的声速比海南的声速要低约10%,可见温度对声速的影响非常显著。这就回答了我们一开始提的第二个问题。不过,由于声速值本身就非常大,对于人们平时交谈时所处的距离来说,10%的声速差异并不会带来什么可以察觉到的变化。
在这一节里边,我们学习了如何推导空气中的声波方程,并了解了得到声波方程和声速值所需要的近似:绝热近似、准静态近似和
 远小于1的近似。这些近似限制了本节结论的适用范围,比如不能用于特别稀薄的空气,不能用在声音频率特别高、声波振幅特别大的情况。我们也介绍了牛顿所犯的错误,并“完成”了牛顿所没能完成的事,不管你是不是物理专业的,都值得为这一件事骄傲。
远小于1的近似。这些近似限制了本节结论的适用范围,比如不能用于特别稀薄的空气,不能用在声音频率特别高、声波振幅特别大的情况。我们也介绍了牛顿所犯的错误,并“完成”了牛顿所没能完成的事,不管你是不是物理专业的,都值得为这一件事骄傲。